"Решение стереометрических задач с практическим содержанием"

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ

ОТДЕЛ ОБРАЗОВАНИЯ ГОРОДА ЕНАКИЕВО

«РЕШЕНИЕ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ

ПРАКТИЧЕСКОГО СОДЕРЖАНИЯ»

Подготовила учитель математики КУ «ОШ I-III ступеней №11 г.Енакиево»

Икаева Марина Александровна

Енакиево 2017

Задачи по стереометрии — прекрасные упражнения, способствующие развитию пространственных представлений, умения логически мыслить, способствующие более глубокому усвоению всего школьного курса математики.

Для овладения и управления современной техникой и технологией нужна серьезная общеобразовательная подготовка, включающая в качестве непременного компонента активные знания по математике .

Школа должна неуклонно повышать эффективность и качество учебной и воспитательной работы, добиваться, чтобы каждый урок способствовал развитию познавательных интересов учащихся и приобретению навыков самостоятельного пополнения знаний.

Одним из возможных путей решения этих серьёзных задач является прикладная ориентация школьного курса математики, которая позволяет вооружить ученика теми знаниями, которые, с одной стороны, разовьют его математическую культуру, а с другой стороны, помогут применять эти знания на практике в будущей трудовой деятельности. Изучая математику, учащиеся должны усвоить и оценить её прикладные возможности и получить основные навыки в приложении этой науки на практике.

Решение практических задач на уроках математики приводит к естественной взаимосвязи теории и практики при преподавании, показывает жизненность и практическую необходимость формирования тех или иных правил, способствует глубокому, не формальному изучению основ математических наук.

Под математической задачей с практическим содержанием (задачей прикладного характера) понимается задача, фабула которой раскрывает приложение математики в смежных учебных дисциплинах, знакомит с ее использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операции.

В работе приводятся примеры и решения стереометрических задач с практическим содержанием, которые используются для закрепления и обобщения различных тем в стереометрии, а также для подготовки к ЕГЭ и ГИА.

Особенностями геометрических задач, отбираемых для включения в ЕГЭ по математике являются:

• Повышение роли наглядности. К каждой задаче предполагается да вать рисунок, позволяющий лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления.

• Повышение роли конструктивных умений учащихся. Включение задач, в которых требуется не только выполнить вычисления, но и провести построения (изображения) искомых геометрических фигур.

• Повышение роли геометрических задач с практической направленностью. Нахождение расстояний до недоступных объектов, величин углов, объемов и площадей поверхностей реальных предметов и др.

Здесь предлагаются примеры задач на нахождение объемов и площадей поверхностей пространственных фигур.

Они проверяют развитие пространственных представлений учащихся, умения проводить построения в пространстве, находить объемы и площади поверхностей многогранников, круглых тел и их комбинаций.

Для успешного решения этих задач требуются знания основных формул для нахождения значений геометрических величин пространственных фигур; умения проводить дополнительные построения на изображениях пространственных фигур, работать с формулами, выполнять преобразования и производить действия с числовыми выражениями в процессе решения задачи.

Рассмотрим задачи на прямоугольный параллелепипед и куб. На пирамиду. На цилиндр, конус, сферу и шар.

В заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о погружении детали в жидкость или о переливании жидкости из одного сосуда в другой.

Вопросы в условии связаны с нахождением объёма погружаемого в жидкость тела или с нахождением какого-либо параметра сосуда. Форма сосуда может быть различной: цилиндр, призма. Далее рассмотрим задачи, взятые из открытого банка задач ЕГЭ по математике.

Что необходимо понимать?

Если жидкость залита в цилиндрический сосуд, то она принимает форму цилиндра. Если она залита в сосуд, имеющий форму призмы, то соответственно принимает форму призмы. Это означает, что формулы для объёмов цилиндра и призмы работают и для объёмов жидкостей помещённых в такие сосуды.

Если жидкость переливается в аналогичный сосуд с меньшим основанием, уровень (высота) жидкости увеличивается; если в сосуд с большим основанием, то уровень жидкости уменьшается.

Рекомендации!

В задачах на погружение детали в жидкость следует найти объём полученный после её погружения, далее найти разность объёмов до и после (если данные в условии это позволяют). Можно такие задачи решать и другим способом, используя закон Архимеда. В задачах, где идёт речь о переливании жидкости в другой сосуд (с уменьшенной или увеличенной площадью основания) помните о том, что сам объём жидкости остаётся неизменным. Вы можете выразить его через площадь основания и высоту (S₁ и H₁) одного сосуда и площадь основания и высоту (S₂ и H₂) другого сосуда, далее полученные выражения приравнять.

При дальнейших преобразованиях получите отношение соответствующих величин – либо площадей оснований, их рёбер, либо высот. Пример такой задачи рассмотрен ниже в статье.

Задача:

В цилиндрический сосуд налили 5000 см³ воды. Уровень жидкости оказался равным 40 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см. Чему равен объем детали? Ответ выразите в см³.

Мы знаем, что объём цилиндра равна произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Высота это есть уровень жидкости.

Итак, из имеющихся данных можем найти площадь основания:

Основание цилиндра у нас величина неизменная, но изменилась высота жидкости (при погружении детали) на 15 сантиметров, то есть она стала  

40 +15 = 55 см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  6875 – 5000 = 1875 см³

Можно решать подобные задачи более рациональным способом.

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/45  исходного объема:

Ответ: 1875

Решить самостоятельно:

Задача:

В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали? Ответ выразите в см³.

Принцип решения тот же самый, что и в предыдущей задаче.

Мы знаем, что объём призмы равен произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Из имеющихся данных можем найти площадь основания призмы:

Основание призмы  не изменилось, но изменилась высота жидкости (при погружении детали)  она стала 24см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  3000 – 2500 = 500 см³

Второй способ:

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20  исходного объема:

Ответ: 500

Решить самостоятельно:

Задача:

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 250 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 5 раз больше, чем у первого? Ответ выразите в см.

В подобных задачах с переливаниями жидкости следует помнить, что объём её остаётся прежним (он не изменен – куда бы её не перелили).

Объем жидкости в данном случае это объём правильной  треугольной призмы  (в её основании лежит правильный треугольник). Он равен произведению  площади основания призмы на высоту:

Суть дальнейших действий сводится к тому, что мы можем выразить объёмы жидкостей в двух призмах: первой и второй (основание которой в 4 раза больше), а затем приравнять полученные выражения, в итоге после преобразований получим отношение двух высот.

Естественно, что высота жидкости уменьшится, если увеличить площадь основания.

Обозначим исходную высоту жидкости Н₁, полученную после переливания Н₂.

Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:

Таким образом, объём залитой жидкости  в первую призму равен:

Площадь основания второй призмы равна:

Объём залитой жидкости  во вторую призму равен:

Найдём отношение высот:

Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.

Или можно сказать так:

При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.

Ответ: 10

Решить самостоятельно:

Задача:

В цилиндрический сосуд, в котором находится 14 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему равен объем детали? Ответ выразите в литрах.

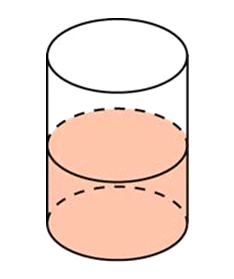
Объём цилиндра равна произведению площади его основания на высоту:

Жидкость в сосуде имеет цилиндрическую объёмную форму.

Уровень жидкости поднялся в 1,1 раза – означает, что высота цилиндра увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также в 1,1 раза (так как зависимость величин  прямо пропорциональна).

Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.

Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.

Ответ: 1,4

Решить самостоятельно:

Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?

Например, если дан начальный объём и высота жидкости (в сосуде формы призмы или цилиндра), то мы можем найти площадь основания. Затем, зная площадь основания и высоту жидкости после погружения детали мы можем найти объём.

Далее вычислить разницу между объёмами не составит труда  (это относится к первым двум задачам). В последней задаче для решения требуется немного логики.

Рассмотри задачи и их решения (слайды 9-15)

Приложение: Стереометрические задачи с практическим содержанием.

1. Сколько досок размером 5 х 0,15 х 0,04 м содержится в штабеле массой 343,2 кг, если плотность древесины 0,52 г/см³?

2. Сколько кубиков с ребром 3 см можно выплавить из свинцового бруска размерами 10х 7 х2 см?

3. Из куска пластилина , который имел форму прямоугольного параллелепипеда с размерами 1*2*4 вылепили куб. найти ребро этого куба.

4. Размеры кирпича 250×120×65 мм.

5. Поле прямоугольной формы площадью 5 га вспахано на глубину 35 см. Сколько кубометров земли перевернули?

6. Три свинцовых куба с ребрами 1см, 6 см, 8 см переплавили в один куб. найти длину ребра этого куба.

7. Для здоровья учеников необходимо, чтобы в классе на каждого ученика приходилось не меньше 6 кубометров воздуха. На сколько учеников рассчитана комната. Размеры которой 10×6×3,5 м?

8. Нужно выкопать прямую канаву длиной 200 м и глубиной 1,5 м. Ширина канавы вверху 3 м, а воле дна 2 м. сколько кубометров грунта необходимо выкопать?

9. Сколько кг краски потребуется для покраски (с учетом пола и потолка) помещения размерами 12 х 5 х 3 метра, если расход краски на 1 м² составляет 250 г?

10. Цилиндрическая емкость радиусом 38 см и высотой 86 см. на две трети заполнена маслом. Сколько литров масла можно долить в эту емкость? Сколько литров масла было первоначально?

11. 25 м медной проволоки имеют массу 100,7 г. Найдите диаметр проволоки (плотность меди 8, 94 г/см3)

12. Насос, подающий воду в паровой котел, имеет два водяных цилиндра. Диаметры цилиндров 80 мм, а ход поршня 150 мм. Чему равна часовая производительность насоса, если каждый поршень делает 50 рабочих ходов в минуту?

13. Свинцовая труба (плотность свинца 11,4 г/см3) с толщиной стенок 4 мм имеет внутренний диаметр 13 см. Какова масса 25 м этой трубы?

14. Цилиндрическая дымовая труба с диаметром 65 см имеет высоту 18 м. Сколько жести нужно для ее изготовления, если на заклепку уходит 10% материала?

15. В цилиндрическую посудину, внутренний диаметр которой 20 см, опущена деталь. При этом уровень воды в посудине поднялся на 12см. найти объем детали.

16. Длины двух круглых колод равны, а их диаметры относятся как 2:3. Как относятся их объемы?

17. Найдите площадь круглого пятна на поверхности моря, образованного кубометром разлитой нефти, если толщина пленки 1 мм.

18. *В цилиндрический сосуд, радиус основания которого 4 см, помещен шар радиуса 3 см. В сосуд наливается вода так, что её свободная поверхность касается поверхности шара(шар не всплывает). Определить толщину того слоя воды, который образуется, если шар вынуть.

19. *Два шарика помещены в цилиндрическую банку, диаметр которой 22 см. Если влить в банку 5 л воды, то покроются ли водой полностью оба шарика, если их диаметры 10 и 14 см?.

20. В цилиндрической посудине жидкость достигает высоты 16 дм. На какой высоте будет уровень жидкости, если её перелить в посудину, диаметр которой в 2 раза больше первого?

21. Сколько метров стальной проволоки в мотке, если его масса 30 кг, а диаметр проволоки 6 мм? Плотность стали 7600кг/м³

22. Столбик ртути в термометре длиной 15,6см весит 5,2 г (удельный вес ртути 13,6) Найти площадь поперечного сечения столбика.

23. Железобетонная панель имеет размеры 600×120×22 см. по всей её длине 6 цилиндрических отверстий, диаметры которых 14 см. Найти массу панели, если плотность материала 2,5т/м³.

24. Сколько тонн стальных труб пошло на сооружение газопровода длиной 4450 мм, если его внешний диаметр 1420 мм, а толщина трубы 22 мм? Плотность стали 7600кг/м³.

25. Сколько квадратных метров бумаги в рулоне, высота которого 85 см, а радиусы 45 см и 2 см. толщина бумаги 0,1 мм.

26. Из цилиндра , высота которого равна диаметру, выточили шар наибольшего объема. Сколько процентов материалов сточено?

27. Из цилиндра, осевое сечение которого – квадрат со стороной 10 см, кузнец сковал шар. Найдите радиус этого шара.

28. Из свинцового шара радиуса 10 мм делают цилиндрический диск, толщиной 3 мм. Найти диаметр этого диска.

29. Сколько шариков диаметром 0,6 см можно отлить из куска свинца, массой 1 кг. Плотность свинца 11,4 кг/дм³.

30. Шар радиусом 6 дм плавает в воде. Найдите высоту части шара, которая выступает из воды, если плотность материала, из которого сделан шар 0,7 г/см3

31. Полуцилиндрический свод подвала имеет 6 м длины и 5,8 м в диаметре. Сколько краски потребуется для окраски полной поверхности подвала при расходе 250г/м2

32. Из круглого листа железа выштампован цилиндрический стакан диаметром 25 см и высотой 50 см. Предполагая, что площадь листа при штамповке не изменилась, найти диаметр листа.

33. Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания 2,5 м, высота 4 м, причем цилиндрическая часть стога имеет высоту 2,2 м. Плотность сена 0,03 г/см3. Определить массу стога сена.

34. Сколько олифы потребуется для окраски внешней поверхности 100 ведер, имеющих форму усеченного конуса с диаметрами оснований 25 см и 30 см и образующей 27,5 см, если на 1 м2 требуется 150 г олифы?

35. Сколько метров стыковых швов пришлось сварить электросварщикам, которые строили газопровод длиной 1450 км, если он был сконструирован из двадцатиметровых труб диаметром 1420 мм?

36. сколько квадратных метров жести пойдет на изготовление водосточной трубы длиной 5 м и диаметром 20 см, если на швы прибавляют 10% площади поверхности трубы?

37. Хватит ли 8500 кв. метров изоляционной ленты для двукратного покрытия ею километра газопровода диаметром 1420 мм.

38. Высота консервной банки цилиндрической формы равна 4 см, а радиус основания 6 см. Сколько таких банок можно изготовить из 15000 кв. метров жести, если 10% материалов идет на отходы и швы?

39. Какова должна быть высота цилиндрической кастрюли с диаметром дна 26 см, чтобы в ней можно было приготовить 0,75 л плодово-ягодного киселя?

40. Диаметр цилиндрического парового котла длиной 3,8 м равен 0,8 м. найдите давление пара на полную поверхность котла, если на 1 см кв. пар давит с силой 10Н.

41. Сколько кв. метров ткани нужно, чтобы пошить конусообразную палатку, высотой 3 м и диаметром 4 м?

42. Будет ли защищен во время грозы дом, высотой 6 м, шириной 8 м и длиной 10 м. если высота громоотвода 7 м, а угол между громоотводом о образующей конуса безопасности 60 градусов.

43. Необходимо разлить 1 л фруктового мусса в конические бокалы высотой 9 см и диаметром основания 8 см. Сколько бокалов потребуется?

44. Куча щебня имеет коническую форму, образующая которой 2 м и угол наклона к поверхности земли 30⁰. Найти объем кучи щебня.

45. 122-миллиметровая бомба даёт при взрыве воронку диаметром в 4 м и глубиной 1,5 м. Какое количество земли (по весу) выбрасывает эта бомба? земли весит 1650 кг.

46. Из жести вырезан сектор радиуса в 20 см с центральным углом в 250hello_html_m28215024.gif и свёрнут в конус. Найти объём конуса.

47. *Посудина имеет форму перевернутого конуса, осевое сечение которого – равносторонний треугольник. В него налита вода так, что когда бросили а посудину металлический шарик радиусов р, поверхность воды оказалась касательной к шарику. На какой высоте будет вода, если вынуть шарик?

48. В Антарктиде приблизительно 30 млн кубометров льда. На сколько метров поднялась бы вода, если бы растаяли все льды. Радиус Земли 6000 км.

49. Радиус Земли равен 6400 км. На какую высоту над горизонтом нужно подняться, чтобы линия горизонта проходила на расстоянии 100 км от наблюдателя.

50. Для окрашивания поверхности цилиндрической формы используется краскопульт типа СО-20В. Определите сколько раз нужно заправить краскопульт, если его размеры: высота равна 70 см, диаметр равен 30 см; размеры поверхности: высота - 30 м, диаметр - 10 м и расход краски на 1 м2 – 0,3 л

Литература:

1. Афанасьева О.М., Бродский Я.С., и др. Дидактические материалы по геометрии . 10-11 классы: Учебное пособие – Тернополь:2004;

2. Геометрия: 11кл.: учебник для общеобразоват. учебных организаций: академ. уровень, профильный уровень/Г.П.Бевз, В.Г.Бевз и др – К.Генеза, 2011.

3. https://ege.sdamgia.ru/