2 Внутренние силовые факторы

ГПОУ «Читинский техникум отраслевых технологий и бизнеса»

Лекция по технической механике

«Внутренние силовые факторы. Метод сечений»

Разработчик: преподаватель Батуев Б. Н.

Чита 2015 г

Метод сечений

- служит для определения внутренних сил упругости, возникающих в результате действия приложенных к деталям внешних сил при расчете деталей машин на прочность.

Суть: тело мысленно разрезается поперечной плоскостью на две части, любая из которых отбрасывается и взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.

Внутренние силы в поперечном сечении прямого бруса.

Рассечем брус поперечным сечением а — а и рас­смотрим равновесие его левой части.

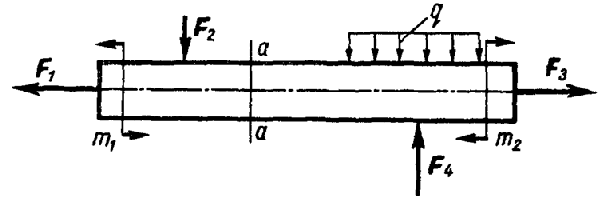
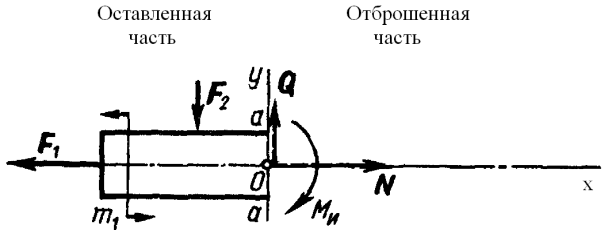
Внутренние силы, действующие в сечении а—а: силы N, Q, приложенные в центре тяжести сечения, момент М_и. Они уравновешивают внешние силы, приложенные к оставленной части бруса.

N - вдоль оси, Q- перпендикулярна этой оси, т. е. в плоскости поперечного сечения. Эти силы + момент М_и = внутренни­е силовые факторы. N – продольная сила, Q — поперечная сила, М_и — изгибающий момент.

Для определения их- 3 уравнения равновесия для оставленной части бруса:

∑X = 0, ∑Y = 0, ∑M = 0.

(ось x по оси бруса).

При пространственной системе сил в поперечном сечении бруса- 6 внутренних силовых факторов. Для определе­ния их- 6 уравнений равновесия оставлен­ной части бруса:

∑X = 0, ∑Y = 0, ∑Z = 0,

∑Mx = 0, ∑My = 0, ∑Mz = 0.

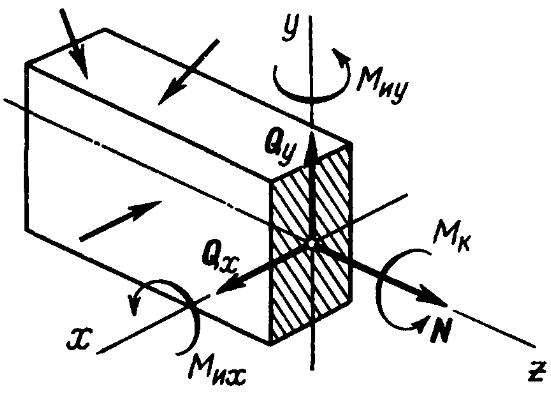
Внутренние силовые факторы: N — продольная сила, Qx, Qy - поперечные силы, М_к — крутящий момент, М_ИY, М_ИZ — изгибающие моменты.

При разных деформациях в поперечном сечении бру­са возникают различные внутренние силы (-овые факторы). Частные случаи:

1. В сечении только продольная сила N. Это деформация растяжение (если сила N - от сечения) или деформация сжатие (если сила N – к сечению).

1. В сечении только поперечная сила Q. Это деформация сдвига.

2. В сечении только крутящий момент М_к. Деформация кручения.

3. В сечении только изгибающий момент М_и. Деформация чистого изгиба. Если в сечении одновременно М_и и Q - изгиб поперечный.

4. Если в сечении одновременно возникает несколько внутрен­них сил (овых факторов) (например, М_и+М_к, М_и+N, и др.), то это- сложная деформация.

Напряжения

- одно из основных понятий сопромата наряду с деформацией. Это характеристика интенсивности внутрен­них сил в сечении.

Рассмотрим какой-ли­бо произвольно нагруженный брус и применим к нему метод сечений.

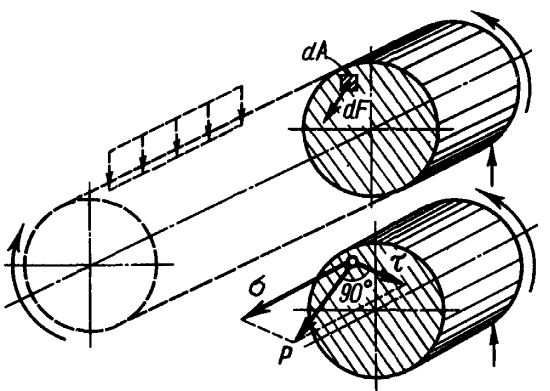
Выделим в сечении dА - бесконечно малая площадь. В его пределах внутренние силы представляют собой систему параллельных сил. Пусть dF - равнодействующая системы сил. Разделив dF на площадь элементарной площадки dА, определим интенсивность внутренних сил, т.е. напряжение р в точках элементарной площадки dА:

p = dF/ dА.

Напряжение – это интенсивность внутренних сил, или внутренняя сила, отнесен­ная к единице площади сечения. Векторная величина.

Единица напряжения:

[p] = [F] / [А] = сила/площадь = Н/м²= паскаль(Па).

Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (МПа):

1 МПа = 10⁶ Па = 1000000Па =1Н/мм².

Числовые значения напряжения, выраженного в МПа и Н/мм², совпадают.

Разложенные векторы напряжения р на 2 составляющие: σ — направленное перпендикулярно плоскости сечения наз-ся нормальным напряжением, τ – лежащее в плоскости сечения, наз-ся касательным напряжением.

Так как угол между нормальным и касательным напряжени­ями всегда равен 90°, то полное напряжение р опре­делится по формуле

р = √ σ²+ τ².

Разложение полного напряжения на нормальное и касатель­ное имеет вполне определенный физический смысл. Как мы убедимся в дальнейшем, в поперечном сечении бруса

при растяжении, сжатии, чистом изгибе действуют только нормаль­ные напряжения (σ),

при сдвиге, кручении — только касательные напряжения (τ).

***

Список использованных источников

1. Атаров Н.М. Сопротивление материалов в примерах и задачах. М.: Инфра-М, 2010.

2. Ксендзов В.А. Техническая механика. М.: КолосПресс, 2010.

3. Эрдеди А.А. и др. Теоретическая механика. Сопротивление материалов: /А.А.Эрдеди, Ю.А.Медведев, Н.А.Эрдеди. – М.: Высш. шк., 2001.