Справочник к учебнику геометрии 7-9

Тема:

«Справочник по геометрии к учебнику 7-9 класса».

Секция: математика, информатика

Адресация проекта:

Учащимся 7-11 классов, учителям –предметникам

Руководитель проекта:

Петросова Светлана Михайловна. учитель математики МОУ СОШ № 16 города-курорта Кисловодска

Участники проекта, возраст участников:

Маилова Лиана, Джерештиева Марина,

учащиеся 9А класса.

1

Начальные геометрические сведения

2

Треугольники

3

Параллельные прямые

4

Соотношение между сторонами и углами треугольника

5

6

Четырехугольник

Площадь

7

Подобие треугольника

8

Векторы

9

Метод координат

10

Окружность

11

Движение

Глава 1. Начальные геометрические сведения

Глава 2. Треугольники

Глава 3. Параллельные прямые

Глава 4. Соотношение между сторонами и углами треугольника

Глава 5. Четырёхугольники

Глава 6. Площадь

Глава 7. Подобные треугольники

Глава 8. Окружность

Глава 9. Векторы

Глава 10. Метод координат

Глава 11. Скалярное произведение векторов

Глава 11. Скалярное произведение векторов

Глава 11. Скалярное произведение векторов

Глава 11. Скалярное произведение векторов

Глава 12. Длина окружности и площадь круга

Глава 13. Движение

Обратите внимание! Это интересно знать…

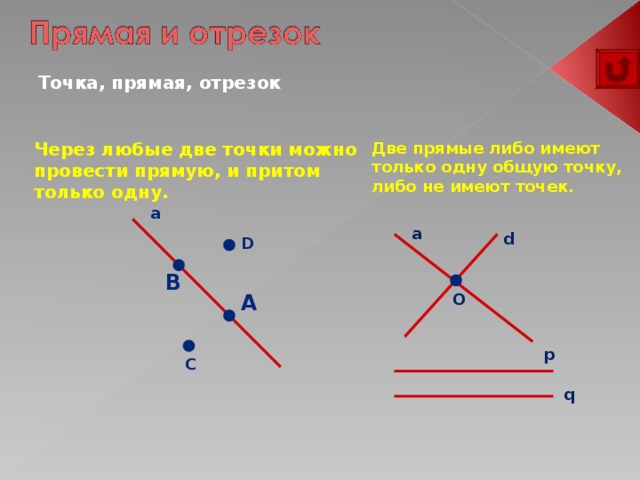
Точка, прямая, отрезок

Две прямые либо имеют только одну общую точку, либо не имеют точек.

Через любые две точки можно провести прямую, и притом только одну.

a

a

d

D

B

A

O

p

C

q

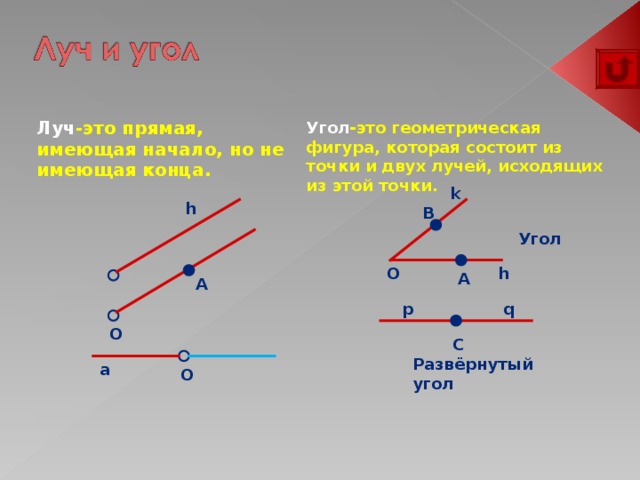
Угол -это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Луч -это прямая, имеющая начало, но не имеющая конца.

k

h

B

Угол

h

O

A

A

q

p

O

C

Развёрнутый угол

a

O

11

Равенство геометрических фигур

Две геометрические фигуры называются равными , если их можно совместить наложением .

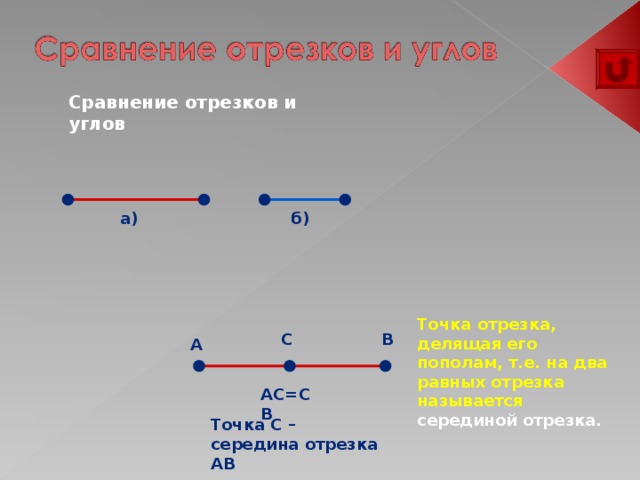
Сравнение отрезков и углов

а)

б)

Точка отрезка, делящая его пополам, т.е. на два равных отрезка называется серединой отрезка.

C

B

A

AC=CB

Точка C – середина отрезка AB

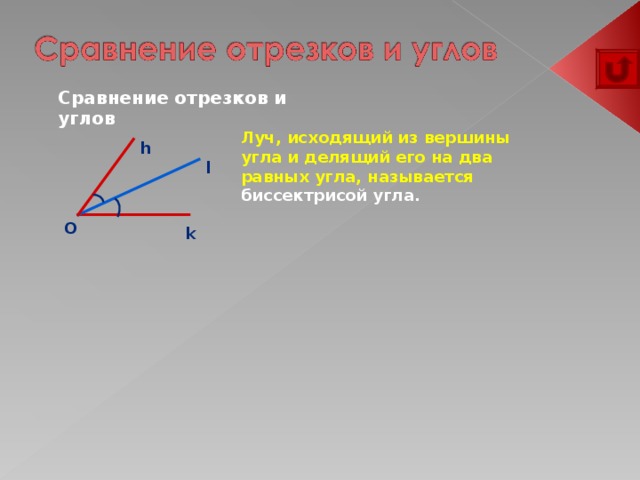
Сравнение отрезков и углов

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

h

l

O

k

1см

Длина отрезка

Единица измерения (также называют масштабным отрезком ).

Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторыми положительным числом.

Равные отрезки имеют равные длины.

Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих отрезков.

Длина отрезка называется также расстоянием между концами этого отрезка.

Градусная мера угла

Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла.

Обычно за единицу измерения углов принимают градус -угол, равный части развёрнутого угла.

1

180

Равные углы имеют равные градусные меры.

Меньший угол имеет меньшую градусную меру.

Когда луч делит угол на два угла, градусная мере всего угла равна сумме градусных мер этих углов.

Транспортир

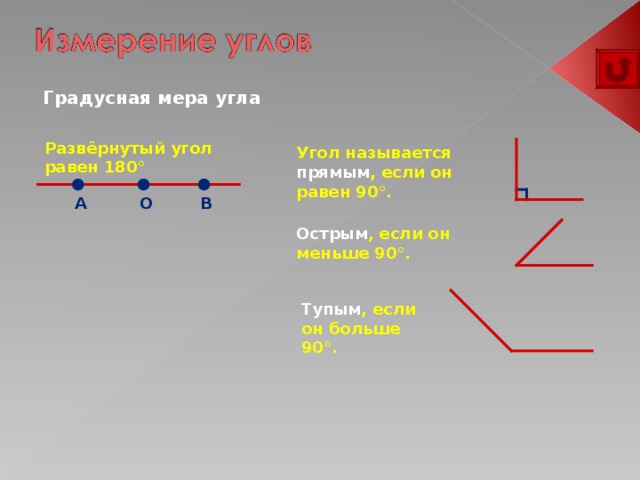
Градусная мера угла

Развёрнутый угол равен 180°

Угол называется прямым , если он равен 90°.

B

A

O

Острым , если он меньше 90°.

Тупым , если он больше 90°.

Смежные и вертикальные углы.

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называется смежными.

B

O

C

A

Сумма смежных углов равна 180°.

2

3

1

Вертикальные углы равны.

4

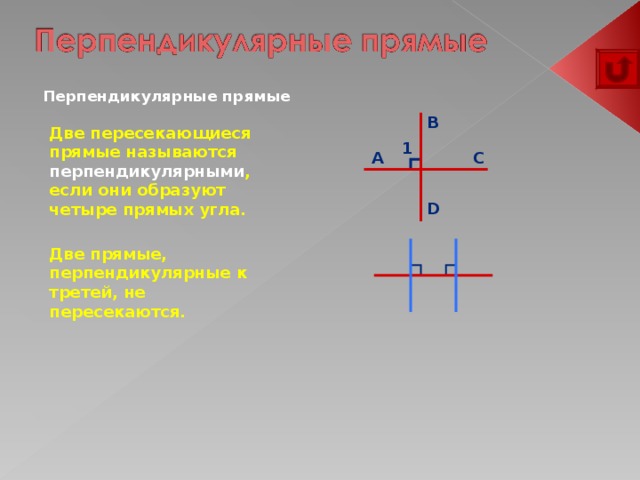
Перпендикулярные прямые

B

Две пересекающиеся прямые называются перпендикулярными , если они образуют четыре прямых угла.

1

A

C

D

Две прямые, перпендикулярные к третей, не пересекаются.

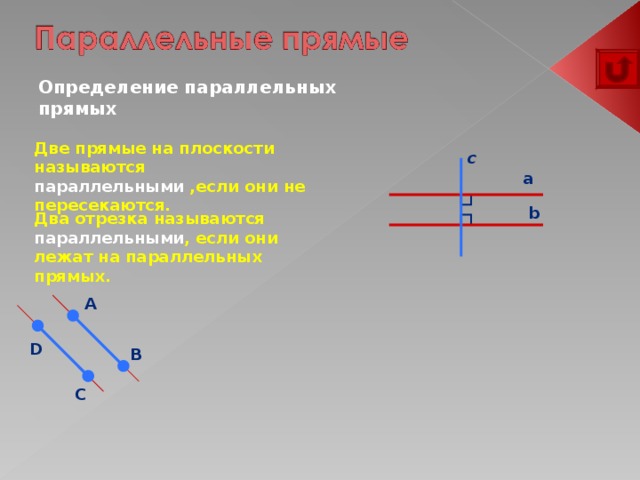
Определение параллельных прямых

Две прямые на плоскости называются параллельными ,если они не пересекаются.

c

a

b

Два отрезка называются параллельными , если они лежат на параллельных прямых.

A

D

B

C

Признаки параллельности двух прямых

• Накрест лежащие углы равны
• Соответственные углы равны
• Односторонние углы равны

Если при пересечении двух прямых секущей накрест лежащие углы раны, то прямые параллельны.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.

Аксиома параллельных прямых

Через любые две точки проходит прямая, и притом только одна

На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

c

Аксиома параллельных прямых

M

a

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

b

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей прямой, то они параллельны.

Теоремы об углах, образованных двумя параллельными прямыми и секущей

Если две параллельные прямые пересечены секущей, то накрест лежащие углы раны.

a

Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

b

c

Теоремы об углах, образованных двумя параллельными прямыми и секущей

Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180º.

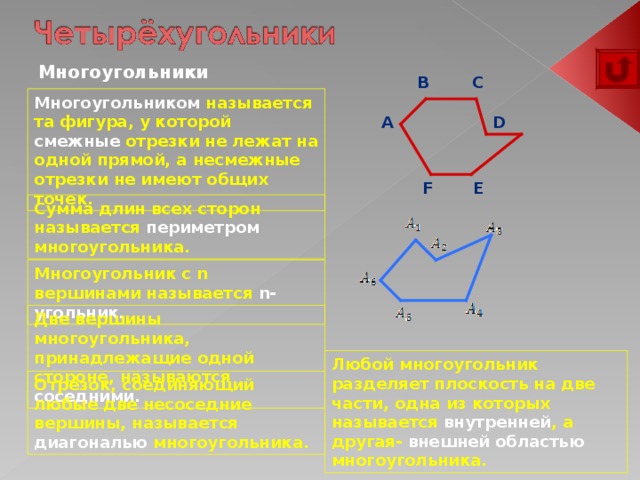
Многоугольники

B

C

Многоугольником называется та фигура, у которой смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

A

D

E

F

Сумма длин всех сторон называется периметром многоугольника.

Многоугольник с n вершинами называется n-угольник.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней , а другая- внешней областью многоугольника.

Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

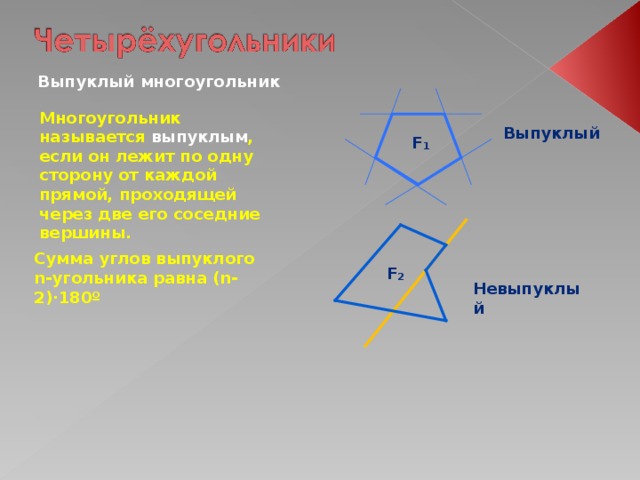
Выпуклый многоугольник

Многоугольник называется выпуклым , если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Выпуклый

F₁

Сумма углов выпуклого n-угольника равна (n-2)∙180º

F₂

Невыпуклый

Четырёхугольник

Две несмежные стороны четырёхугольника называются противоположными.

Две вершины, не являющиеся соседними, также называются противоположными.

Сумма углов выпуклого четырёхугольника равна 360º

Параллелограмм

C

B

Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

D

A

B

C

В параллелограмме противоположные стороны равны и противолежащие углы равны.

D

A

C

B

Диагонали параллелограмма точкой пересечения делятся пополам.

A

D

Признаки параллелограмма

Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.

Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

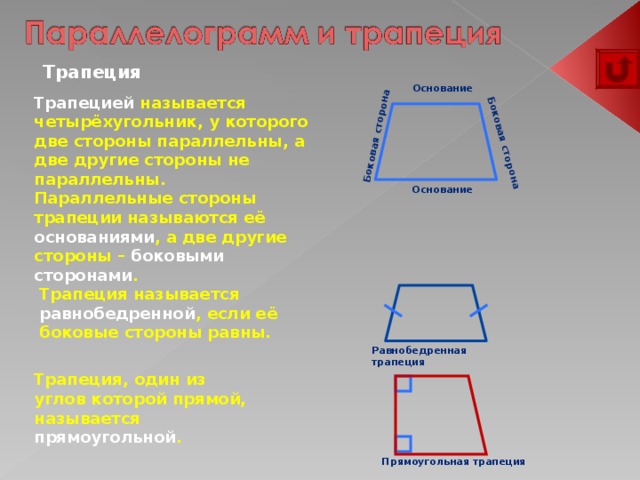
Боковая сторона

Боковая сторона

Трапеция

Основание

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основание

Параллельные стороны трапеции называются её основаниями , а две другие стороны – боковыми сторонами .

Трапеция называется равнобедренной , если её боковые стороны равны.

Равнобедренная трапеция

Трапеция, один из углов которой прямой, называется прямоугольной .

Прямоугольная трапеция

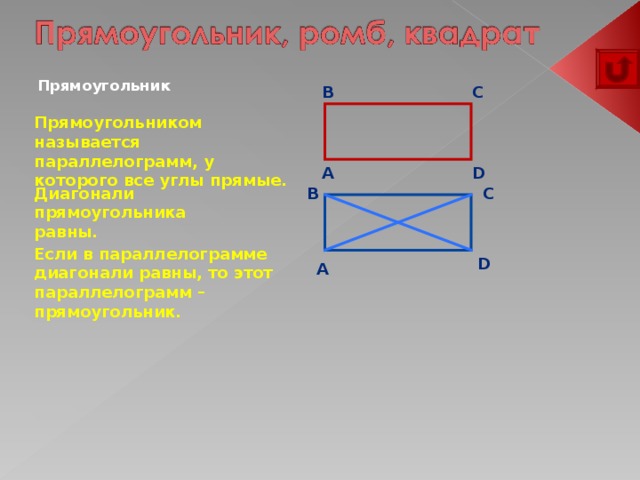
Прямоугольник

B

C

Прямоугольником называется параллелограмм, у которого все углы прямые.

A

D

C

Диагонали прямоугольника равны.

B

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

D

A

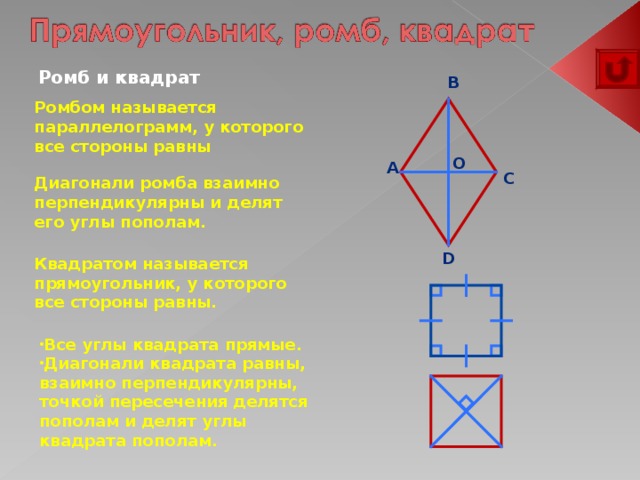
Ромб и квадрат

B

Ромбом называется параллелограмм, у которого все стороны равны

O

A

C

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

D

Квадратом называется прямоугольник, у которого все стороны равны.

• Все углы квадрата прямые.
• Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Осевая и центральная симметрии

A

Две точки называются симметричными относительно прямой a, если эта прямая проходит через середину отрезка AA₁

и перпендикулярна к нему.

a

A₁

Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричной ей точка относительно прямой a также принадлежит симметрии фигуры.

N

M₁

M

Фигура называется симметричной относительно точки O, если для каждой точки фигуры симметричной ей точка относительно точки O также принадлежит этой фигуре. Точка O называется центром симметрии фигуры.

O

N₁

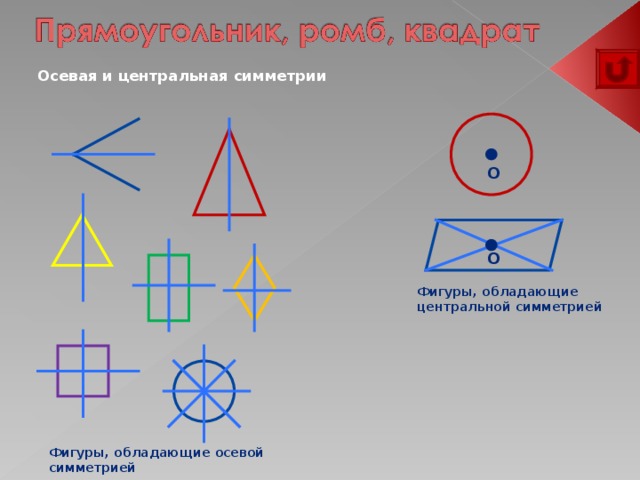
Осевая и центральная симметрии

O

O

Фигуры, обладающие центральной симметрией

Фигуры, обладающие осевой симметрией

Пропорциональные отрезки

Отношением отрезков AB и CD называется

отношение их длин, т. е.

Говорят, что отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D₁

B

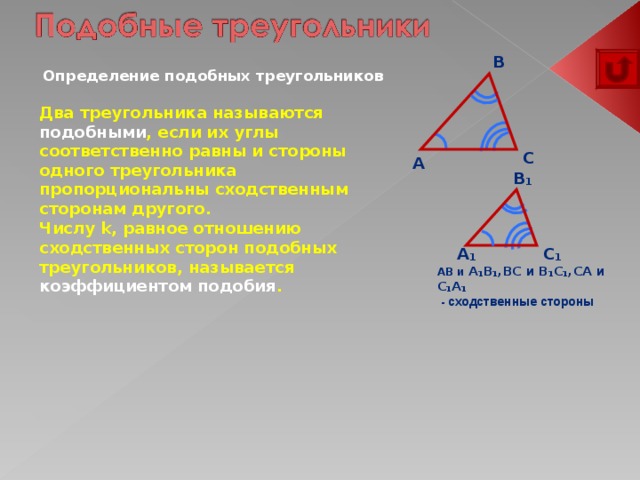
Определение подобных треугольников

Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

C

A

B₁

Числу k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия .

A₁

C₁

AB и A ₁B₁,BC и B₁C₁,CA и C₁A₁

- сходственные стороны

Отношение площадей подобных треугольников

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Первый признак подобия треугольников

C

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

A

B

C₁

B₁

A₁

Второй признак подобия треугольников

C₁

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

B₁

A₁

C

A

B

Третий признак подобия треугольников

C₁

Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

B₁

A₁

C

A

B

Средняя линия треугольника

B

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

N

M

C

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

A

C

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

B₁

A₁

O

A

B

Пропорциональные отрезки в прямоугольном треугольнике

C

Отрезок XY называется средним пропорциональным (или средним геометрическим ) для отрезков AB и CD, если

D

B

A

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведённой из вершины прямого угла.

О подобии произвольных фигур

Фигуры F и F ₁ называются подобными , если каждой точке F можно сопоставить точку фигуры F₁ так, что для любых двух точек M и N фигуры F и сопоставленных им точек M₁ и N₁ фигуры F₁ выполняется равенство , где k одно и тоже положительное число для всех точек.

M

M₁

O

F

F₁

Число k называется коэффициентом подобия фигур F и F ₁.

Фигуры F и F ₁ называются центрально - подобными.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Обозначение:

sin α, cos α, tg α

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Тангенс угла равен отношению синуса к косинусу этого угла.

Основное тригонометрическое тождество:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

Значение синуса, косинуса и тангенса для углов 30 º , 45 º и 60 º

Вектор AB

Конец вектора

Понятие вектора

B

Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором .

Начало вектора

A

Любая точка плоскости также является вектором. В этом случае вектор называется нулевым .

Длина вектора обозначается

так:AB (|а|).Длина нулевого вектора считается равной нулю:

|0|=0

Равенство векторов

Векторы

Неколлинеарные

Коллинеарные

Векторы называются неколлинеарными, если они либо не лежат на одной прямой, либо на параллельных прямых.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.

Сонаправленные

Противоположно направленные

Векторы называются равными , если они сонаправлены и их длины равны.

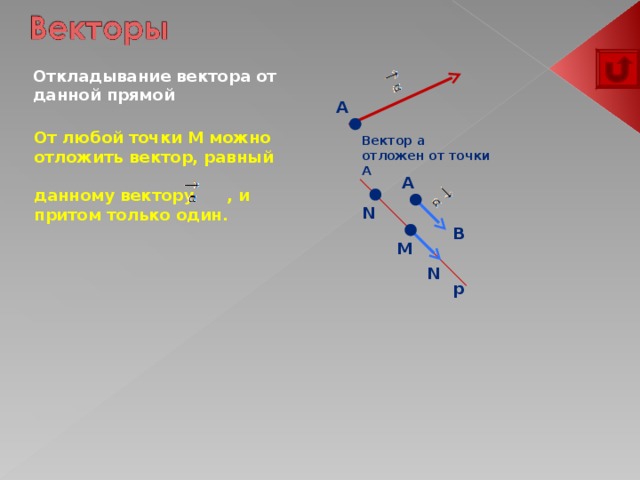
Откладывание вектора от данной прямой

A

От любой точки M можно отложить вектор, равный

данному вектору , и притом только один.

Вектор a отложен от точки A

A

N

B

M

N

p

Сумма двух векторов

Правило треугольника

Для любого вектора справедливо равенство

Законы сложения векторов. Правило параллелограмма.

Для любых векторов , и справедливы равенства:

• (переместительный закон).
• (сочетательный закон).

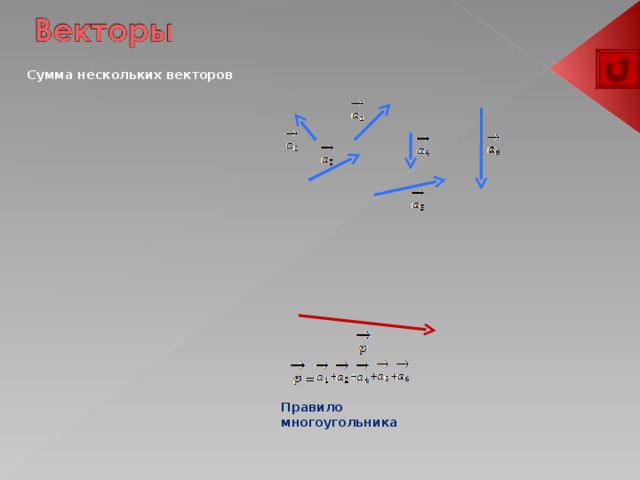
Сумма нескольких векторов

Правило многоугольника

Вычитание векторов

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Для любых векторов и справедливо равенство - = +(- ).

Произведение вектора на число

Произведением нулевого

вектора на число k называется

такой вектор , длина которого

равна |k|· | |, причём векторы

и сонаправлены при k≥0 и противоположно направлены при k

Для любых чисел k, l

и любых векторов , справедливы равенства:

• (kl) =k(l ) (сочетательный закон).
• (k+l) =k +l (Первый распределительный закон).
• K( + )=k +k (Второй распределительный закон).

Средняя линия трапеции

B

C

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

M

N

A

D

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Синус, косинус, тангенс

Для любого угла a

из промежутка 0º≤a≤180º синусом угла a называется

у

h

C

N

M

y

Тангенсом угла a (a=90º)

называется отношение , т.е.

a

x

Х

O

B

D

Основное тригонометрическое тождество. Формулы приведения

Основное тригонометрическое тождество

Формулы приведения

Формулы для вычисления координат точки

A(x ; y)

x =|OA|· sin a

y =|OA|· cos a

Соотношение между сторонами и углами треугольника

Теорема о площади треугольника

Площадь треугольника равна половине произведения двух его сторон на синус угла между этими сторонами.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

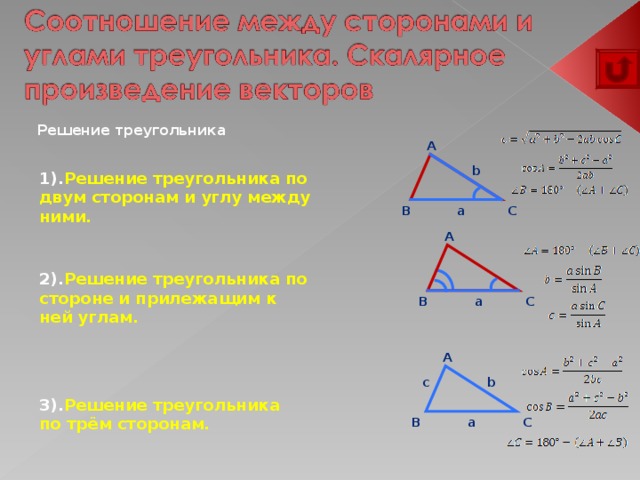
Решение треугольника

A

b

1). Решение треугольника по двум сторонам и углу между ними.

a

C

B

A

2). Решение треугольника по стороне и прилежащим к ней углам.

a

C

B

A

c

b

3). Решение треугольника по трём сторонам.

a

C

B

Угол между векторами

a

Градусную меру угла обозначим буквой a и будем говорить, что угол между

векторами и равен a.

Два вектора называются перпендикулярными, если угол между ними равен 90º.

Скалярное произведение векторов

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

·

=

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора равен квадрату его длины.

Скалярное произведение в координатах

Скалярное произведение векторов

{x₁;y₁} и {x₂;y₂} выражается формулой

·

Ненулевые векторы {x ₁;y₁} и {x₂;y₂} перпендикулярны тогда и только тогда, когда x₁x₂+y₁y₂=0

Косинус угла a между ненулевыми

векторами {x ₁;y₁} и {x₂;y₂} выражается формулой

·

Свойства скалярного произведения векторов

Для любых векторов , , и любого числа k справедливы соотношения:

• ²≥0 при ≠ .
• · = · (переместительный закон).
• ( + )· = · + · (распределительный закон).
• (k )· =k( · )(сочетательный закон).

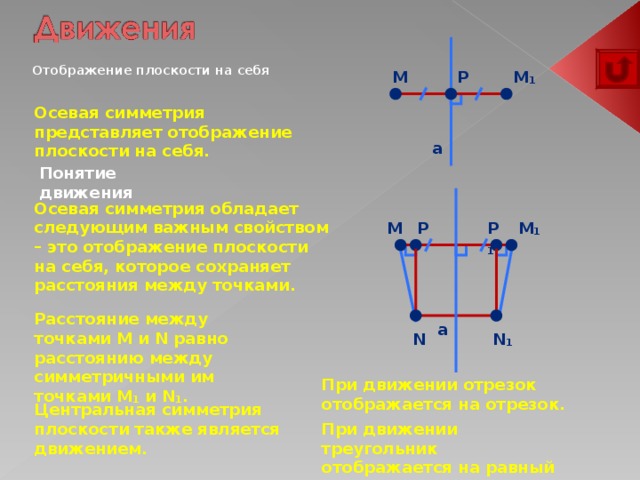
Отображение плоскости на себя

M

P

M ₁

Осевая симметрия представляет отображение плоскости на себя.

a

Понятие движения

Осевая симметрия обладает следующим важным свойством – это отображение плоскости на себя, которое сохраняет расстояния между точками.

M

P ₁

M ₁

P

Расстояние между точками M и N равно расстоянию между симметричными им точками M ₁ и N ₁.

a

N

N ₁

При движении отрезок отображается на отрезок.

Центральная симметрия плоскости также является движением.

При движении треугольник отображается на равный ему треугольник.

Наложения и движения

Наложение – это отображение плоскости на себя.

При наложении различные точки отображаются в различные точки.

Любое наложение является движением плоскости.

Любое движение является наложением.

При наложении любая фигура отображается на равную ей фигуру.

Параллельный перенос

M ₁

N ₁

Пусть - данный вектор. Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M ₁, что вектор равен вектору .

M

N

Параллельный перенос является движением.

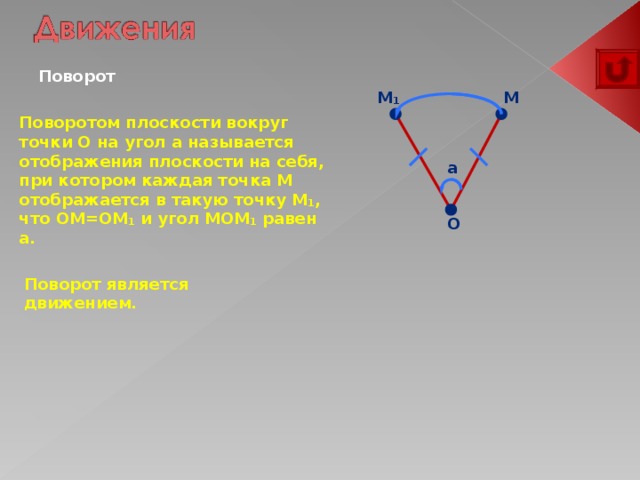
Поворот

M ₁

M

Поворотом плоскости вокруг точки O на угол a называется отображения плоскости на себя, при котором каждая точка M отображается в такую точку M ₁, что OM=OM₁ и угол MOM₁ равен a.

a

O

Поворот является движением.

• Параллельные прямые

• Четырёхугольники

• Подобные треугольники

• Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.

• Если при пересечении двух прямых a и b секущей накрест лежащие углы не равны, то прямые a и b пересекаются.

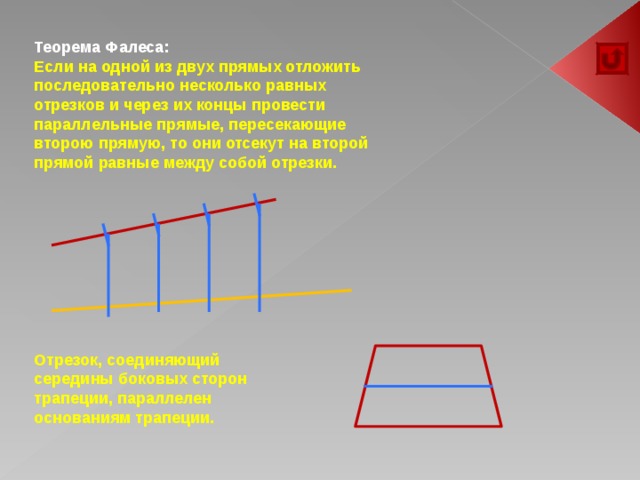
Теорема Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие второю прямую, то они отсекут на второй прямой равные между собой отрезки.

Отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.

Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Отношение сходственных сторон подобных треугольников равно отношению высот, проведённых к этим сторонам.