Становление математической функциональной грамотности младшего школьника
«Задачами развития математического
образования в Российской Федерации являются: модернизация содержания учебных программ математического образования на всех уровнях (с обеспечением их преемственности) исходя из потребностей обучающихся и потребностей общества во всеобщей математической грамотности...; обеспечение отсутствия пробелов в базовых знаниях для каждого обучающегося...»
Концепция развития математического образования в Российской Федерации (утв. распоряжением
Правительства РФ от 24 декабря 2013 г. N 2506-р)

Предметные результаты освоения основной образовательной программы начального общего образования должны отражать:
математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценки их количественных и пространственных отношений;
приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно- практических задач».
ФГОС НОО, с.11

Цель изучения математики
 (для обучающегося):
(для обучающегося):


получать научиться
информацию размышлять
успешно продолжить обучение в 5 классе
5

 Благодаря электричеству, подаренному солнцем, можно ежедневно проезжать
Благодаря электричеству, подаренному солнцем, можно ежедневно проезжать
30 километров. Некоторые авто способны разгоняться до 89 км/ч. Этот автомобиль
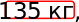
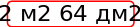 победил в гонке 2017. Солнечная батарея авто
победил в гонке 2017. Солнечная батарея авто
весит её площадь
«Функциональная математическая грамотность включает в себя математические компетентности, которые можно формировать через специально разработанную систему задач:
группа – задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления;
группа – задачи, в которых требуется установить
связи и интегрировать материал из разных областей математики;
группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую
средствами математики, построить модель решения»
Математическая грамотность младшего школьника
как компонент функциональной грамотности трактуется как:
и повседневной жизни;
потребность и умение применять математику в повседневных (житейских) ситуациях: находить, анализировать математическую информацию об объектах окружающей действительности, рассчитывать стоимость (протяженность, массу);
способность различать математические объекты (числа,
величины, фигуры), устанавливать математические отношения (длиннее-короче, быстрее-медленнее), зависимости (увеличивается, расходуется), сравнивать, классифицировать;
(алгоритму), решать учебные задачи, связанные с измерением, вычислениями, упорядочиванием, формулировать суждения с использованием математических терминов, знаков.
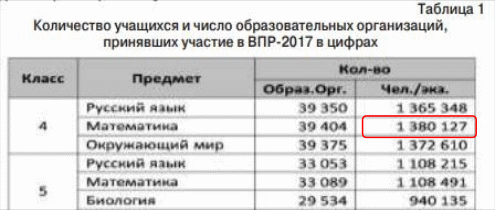

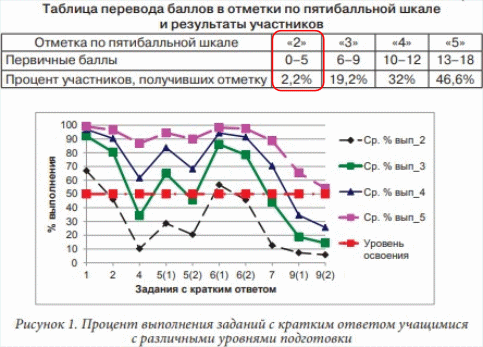
1 380 000 : 100 2,2 = 30 360 (учащихся)


 Содержание
Содержание
Что будет знать и уметь Ваш ребёнок:
выделять и анализировать отдельные признаки и свойства объектов, осмысливать увиденное, активно включать в процесс восприятия мыслительную деятельность;
понимать значение слов и учиться самому формулировать ответы, используя новые слова и словосочетания:
одинаковые по размеру (по цвету, по форме) и др.
рассказывать о последовательности при поиске фрагментов картинки;
объяснять свои действия по ходу выполнения задания.
Виноградова, Н. Ф. Концепция начального образования : «Начальная
школа XXI века» / Н. Ф. Виноградова. — М. : Вентана-Граф,
ISBN 978-5-360-08690-1

2017. — 64 с. : ил.
Обязательные виды деятельности младшего школьника

 (научная школа Н.Ф. Виноградовой) сенсорная деятельность поисково-исследовательская
(научная школа Н.Ф. Виноградовой) сенсорная деятельность поисково-исследовательская
 коммуникативная
коммуникативная

контрольно-оценочная
14
В чем проявляется направленность обучения на
формирование универсальных учебных действий для повышения качества математической грамотности младшего школьника?
Универсальные учебные действия как результат
 обучения в начальной школе: содержание и методика
обучения в начальной школе: содержание и методика
формирования универсальных учебных действий младшего школьника; под ред.
Н.Ф.Виноградовой /
[авт. Н.Ф. Виноградова,
Е.Э. Кочурова, М.И. Кузнецова, В.Ю. Романова, О.А. Рыдзе,
И.С. Хомякова]. – ФГБНУ
«Институт стратегии развития образования РАО», 2016. – 224 с.
Операциональная характеристика регулятивных универсальных учебных действий,
связанных с контролем и коррекцией
| Универсальное учебное действие | Операции, входящие в данное действие (осуществляет обучающийся) |
|
|
| Контроль конечного результата собственной/чужой деятельности и его корректировка | сопоставляю (сравниваю) с правильным ответом; (свою и/или чужую); - исправляю ошибку; – делаю вывод, как избежать такой ошибки в будущем. |
В чем проявляется особое значение педагогической диагностики в повышении качества математической грамотности младшего школьника?
ПЕДАГОГИЧЕСКАЯ ДИАГНОСТИКА ГОТОВНОСТИ К
ШКОЛЬНОМУ ОБУЧЕНИЮ: ПОДХОДЫ И РЕЗУЛЬТАТЫ
Кочурова Е.Э., Кузнецова М.И.
Начальное образование. 2016. № 1. С. 17-23.
ПЕДАГОГИЧЕСКАЯ ДИАГНОСТИКА
Журова Л.Е., Кочурова Е.Э., Евдокимова А.О., Кузнецова М.И.
Русский язык. Математика: 1 класс. Москва. 2013.

Предлагаемая система
диагностических работ позволит определить:
универсальных учебных действий;
педагогических решений о дальнейшем ходе обучения.
Педагогическая диагностика

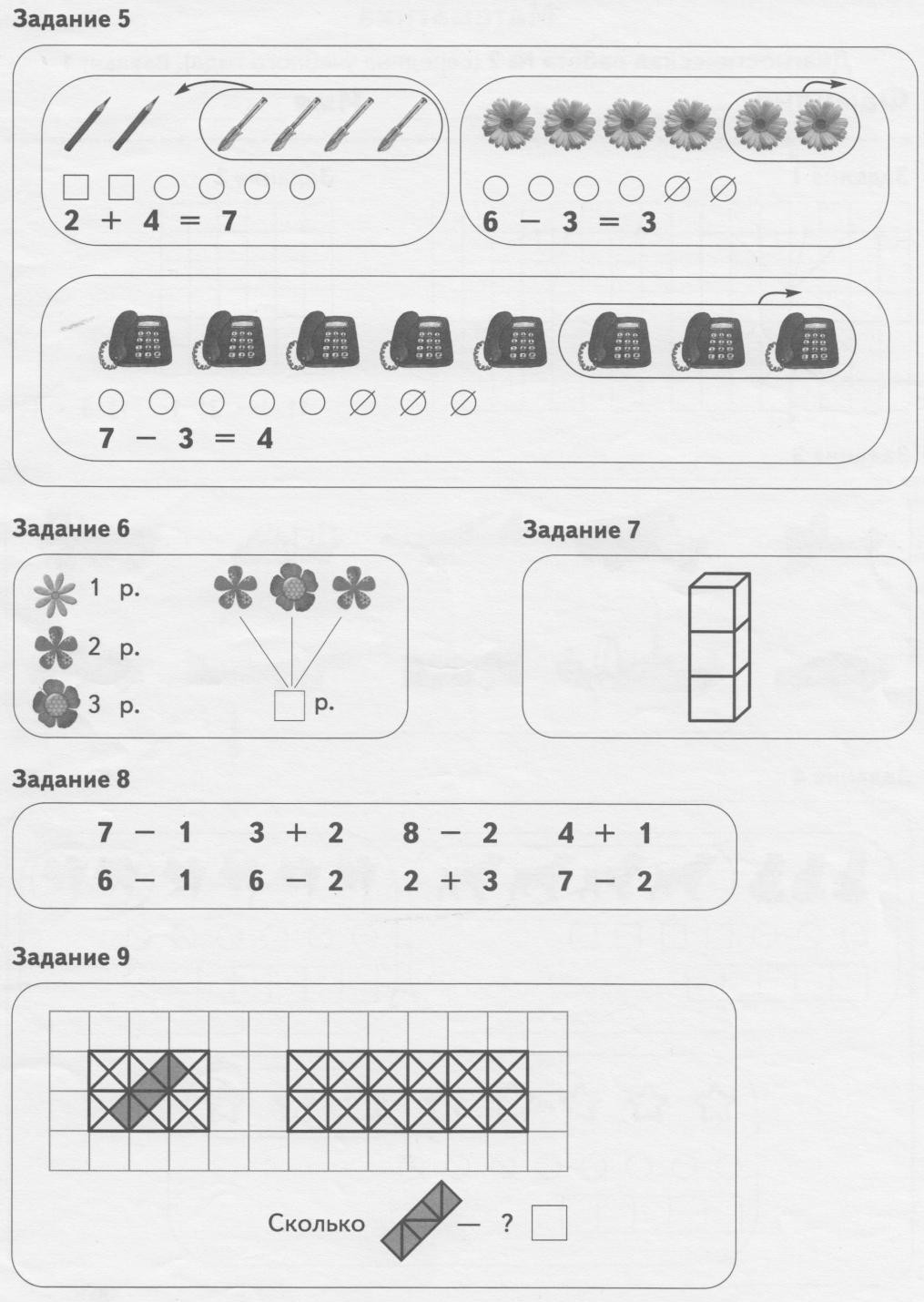 1 класс середина года (математика)
1 класс середина года (математика)
| 4 класс Школа 17 декабря |
|
| 1 Сравне ние многоз начных чисел Нестан дартная ситуаци я. | 2 Поиск ошибок в алгорит ме умноже ния | 3 Примен ение алгорит ма умноже ния для восстан овления пример а. | 4 Первы й «шаг» алгори тма делени я | 5 Примене ние алгоритм а деления | 6 Оценка частного в примера х на деление с остатком | 7 Определ ение «шагов» алгоритм а выполне ния действий в числово м выражен иии | 8 Примен ение математ ич термин ологии: делимо е, делител ь, и др. | 9 – 10 – 11 Анализ текста задачи и готового решения. Выбор двух верных решений из трёх возможных. Восстановление недостающих действий в решении задачи ( 11 ) | 12-13 Анализ геометрическ ой фигуры: длина стороны, периметр, площадь | 14 Констру ктивные умения, примене ние знаний о площади и перимет ре. | Все го Мах 42 |
| Ш. А. | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 41 |
Результаты выполнения диагностической работы по математике 4 класс (середина учебного года) 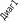


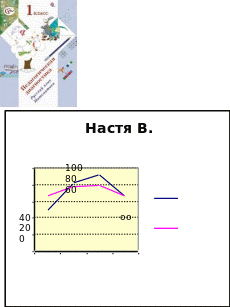
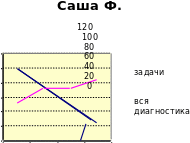 Способы представления результатов педагогической диагностики
Способы представления результатов педагогической диагностики


Какое влияние оказывает осуществление коррекционно-развивающей работы в рамках
«Начальная школа ХХI века» для повышения качества математической грамотности младшего школьника?
 Цель: выявить умение анализировать условие задачи, в которой есть избыточное данное.
Цель: выявить умение анализировать условие задачи, в которой есть избыточное данное.
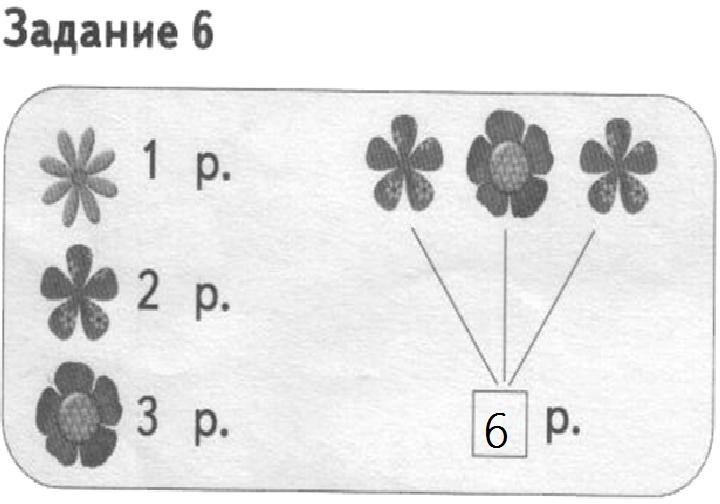
предполагает
вариативность темпа изучения материала,
разнообразие и адресность учебных заданий,
выбор разных видов деятельности,
определение характера и степени дозировки помощи со стороны учителя
с учетом результатов предварительной
педагогической диагностики учащихся.
 Виды педагогической поддержки: показ способа решения, образца рассуждения и оформления:
Виды педагогической поддержки: показ способа решения, образца рассуждения и оформления:
памятки, планы, алгоритмы, способы работы;
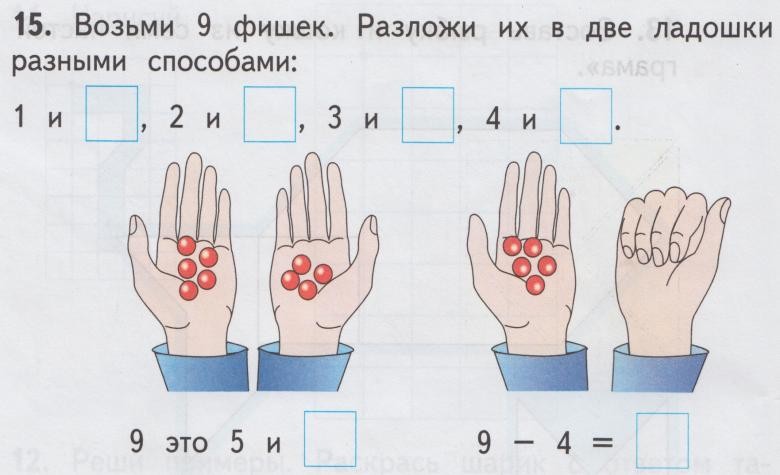 наглядные опоры, иллюстрации,
наглядные опоры, иллюстрации,
модели;


 «Дружим с математикой» 2, 3, 4 класс
«Дружим с математикой» 2, 3, 4 класс
|
| №16 | №17 | №18 |
|
|
| Ученик |

|

|

|
| Учитель |

|

|

|
Формирование самоконтроля и самооценки:
Закрасьте: Ученик:
красным – задание выполнил
правильно;
желтым – сомневаюсь в
правильности решения.
Учитель: красным – задание выполнил верно;
желтым – допущена ошибка
(ошибки), постарайся её найти.
28
 Программа «Занимательная математика»
Программа «Занимательная математика»
// Сборник программ внеурочной деятельности: 1—4 классы /
под ред. Н. Ф. Виноградовой. — М.:
Вентана-Граф, 2016.
МЕТОДИКА ВНЕУРОЧНОЙ РАБОТЫ Кочурова Е.Э.
Начальная школа. 2016. № 4. С. 72-83.

 Центры деятельности:
Центры деятельности:
«Математические «Конструкторы» игры»
«Математические
«Занимательные
задачи»
 головоломки» Задания на компьютере»
головоломки» Задания на компьютере»
30






Универсальные учебные действия
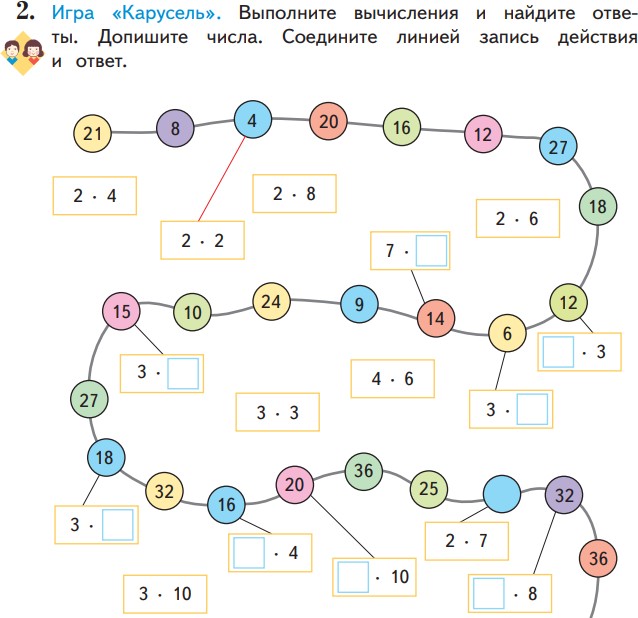
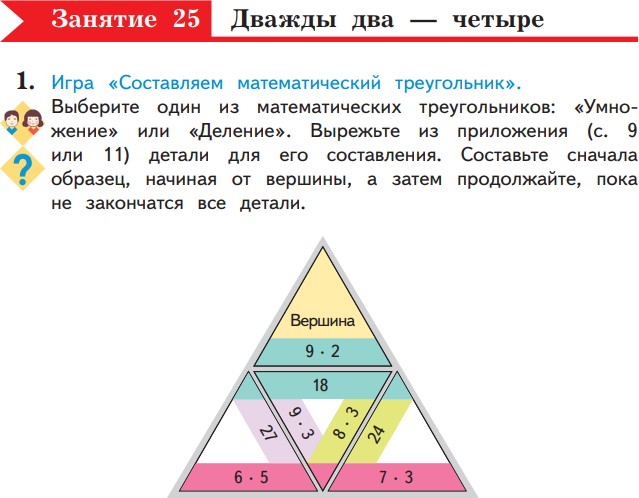
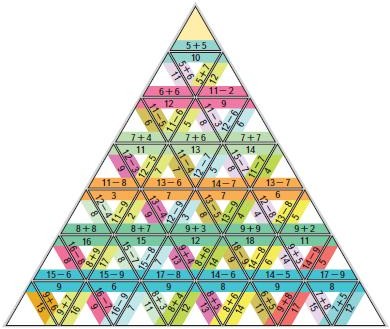
Сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания.
Моделировать в процессе совместного обсуждения алгоритм решения числового кроссворда; использовать его в ходе
самостоятельной работы.
Применять изученные способы учебной работы и приёмы вычислений для работы с числовыми головоломками.





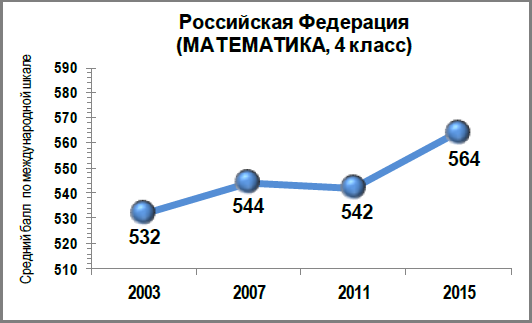
РЕЗУЛЬТАТЫ МЕЖДУНАРОДНОГО ИССЛЕДОВАНИЯ TIMSS 2015 4 КЛАСС

В соответствии с международными стандартами исследования TIMSS 2015 результаты российских учащихся 4 классов по математике (564 балла) существенно превышают среднее значение международной шкалы TIMSS (500 баллов) .
Международное исследование TIMSS подтвердило позитивные эффекты реализации ФГОС начального образования: российские четвероклассники показали в 2015 году подъем уровня подготовки по математике на 21 балл.
Проверочные тестовые работы: русский язык, математика, чтение

 Предлагаемые тесты позволяют выяснять уровень математической грамотности младших
Предлагаемые тесты позволяют выяснять уровень математической грамотности младших
школьников, оканчивающих соответствующий класс (общие для всех программ начальной школы).

 Тестовые задания составлены таким образом, чтобы одновременно выяснялась и сформированность учебных умений – умения воспринимать учебную задачу, контролировать и корректировать собственные действия по ходу выполнения задания, использовать свои знания в новой, нестандартной ситуации.
Тестовые задания составлены таким образом, чтобы одновременно выяснялась и сформированность учебных умений – умения воспринимать учебную задачу, контролировать и корректировать собственные действия по ходу выполнения задания, использовать свои знания в новой, нестандартной ситуации.
Концепция развития математического образования в Российской Федерации (утв. распоряжением Правительства РФ от 24 декабря 2013 г. N 2506-р)
I. Значение математики в современном мире и в России
«Математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса. Изучение математики играет системообразующую роль в образовании, развивая познавательные способности человека, в том числе к логическому мышлению, влияя на преподавание других дисциплин. Качественное математическое образование необходимо каждому для его успешной жизни в современном обществе. Успех нашей страны в XXI веке, эффективность использования природных ресурсов, развитие экономики, обороноспособность, создание современных технологий зависят от уровня математической науки, математического образования и математической грамотности всего населения, от эффективного использования современных математических методов».







 Предметные результаты освоения основной образовательной программы начального общего образования должны отражать:
Предметные результаты освоения основной образовательной программы начального общего образования должны отражать: 
 (для обучающегося):
(для обучающегося):


 Благодаря электричеству, подаренному солнцем, можно ежедневно проезжать
Благодаря электричеству, подаренному солнцем, можно ежедневно проезжать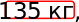
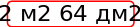 победил в гонке 2017. Солнечная батарея авто
победил в гонке 2017. Солнечная батарея авто



 Содержание
Содержание 2017. — 64 с. : ил.
2017. — 64 с. : ил.  (научная школа Н.Ф. Виноградовой) сенсорная деятельность поисково-исследовательская
(научная школа Н.Ф. Виноградовой) сенсорная деятельность поисково-исследовательская обучения в начальной школе: содержание и методика
обучения в начальной школе: содержание и методика

 1 класс середина года (математика)
1 класс середина года (математика)



 Способы представления результатов педагогической диагностики
Способы представления результатов педагогической диагностики

 Цель: выявить умение анализировать условие задачи, в которой есть избыточное данное.
Цель: выявить умение анализировать условие задачи, в которой есть избыточное данное.
 Виды педагогической поддержки: показ способа решения, образца рассуждения и оформления:
Виды педагогической поддержки: показ способа решения, образца рассуждения и оформления: наглядные опоры, иллюстрации,
наглядные опоры, иллюстрации,

 «Дружим с математикой» 2, 3, 4 класс
«Дружим с математикой» 2, 3, 4 класс

 Программа «Занимательная математика»
Программа «Занимательная математика»
 Центры деятельности:
Центры деятельности: головоломки» Задания на компьютере»
головоломки» Задания на компьютере»















 Предлагаемые тесты позволяют выяснять уровень математической грамотности младших
Предлагаемые тесты позволяют выяснять уровень математической грамотности младших
 Тестовые задания составлены таким образом, чтобы одновременно выяснялась и сформированность учебных умений – умения воспринимать учебную задачу, контролировать и корректировать собственные действия по ходу выполнения задания, использовать свои знания в новой, нестандартной ситуации.
Тестовые задания составлены таким образом, чтобы одновременно выяснялась и сформированность учебных умений – умения воспринимать учебную задачу, контролировать и корректировать собственные действия по ходу выполнения задания, использовать свои знания в новой, нестандартной ситуации.









