Հայաստան, Գյումրի
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 25.07.2020 19:09
Պողոսյան Արմինե Ռազմիկի
Մաթեմատիկայի ուսուցչուհի
56 лет
349
123 204 
Местоположение
Специализация
Թվային ֆունկցիաների հատկությունները
Категория:
Алгебра
28.06.2020 16:55
Просмотр содержимого документа
«Թվային ֆունկցիաների հատկությունները»
1. у = f(-x) ֆունկցիայի գրաֆիկը
у=f(−x) ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=f(−x) և у=f(x) ֆունկցիաների գրաֆիկները համաչափ են օրդինատների առանցքի նկատմամբ:
Այս նկարում կետագծով նշված է \(у = f(x)\) ֆունկցիայի գրաֆիկը, իսկ հոծ գծով՝ նրան օրդինատների առանցքի նկատմամբ համաչափ \(у = f(-x)\) ֆունկցիայի գրաֆիկը:
2. у = - f(x) ֆունկցիայի գրաֆիկը
у=−f(x) ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=−f(x) և у=f(x) ֆունկցիաների գրաֆիկները համաչափ են աբսցիսների առանցքի նկատմամբ:
Այս նկարում կետագծով նշված է \(у = f(x)\) ֆունկցիայի գրաֆիկը, իսկ հոծ գծով՝ նրան աբսցիսների առանցքի նկատմամբ համաչափ \(у = - f(x)\) ֆունկցիայի գրաֆիկը:
3. у = |f(x)| ֆունկցիայի գրաֆիկը
у=|f(x)| ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=|f(x)| ֆունկցիայի գրաֆիկը у=f(x) ֆունկցիայի գրաֆիկի միջոցով կառուցելիս պետք է՝
1) վերցնել у=f(x) ֆունկցիայի գրաֆիկի այն մասը, որը աբսցիսների առանցքի վրա է կամ գտնվում է դրանից վեր,
2) աբսցիսների առանցքից ցած գտնվող մասը համաչափ արտապատկերել աբսցիսների առանցքի նկատմամբ:
Դիցուք, այս նկարում պատկերված է у=f(x) ֆունկցիայի գրաֆիկը:
у=f(x) ֆունկցիայի գրաֆիկի այն մասը, որը աբսցիսների առանցքի վրա է կամ դրանից վեր է չենք փոփոխում, ցած գտնվող մասը՝ համաչափ արտապատկերում ենք աբսցիսների առանցքի նկատմամբ:
Ստանում ենք у=|f(x)| ֆունկցիայի գրաֆիկը՝
4. у = f(|x|) ֆունկցիայի գրաֆիկը
у=f(|x|) ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=f(|x|) ֆունկցիայի գրաֆիկը у=f(x) ֆունկցիայի գրաֆիկի միջոցով կառուցելիս պետք է՝
1) ոչ բացասական x-երի համար կառուցել у=f(x) ֆունկցիայի գրաֆիկը,
2) ստացված գրաֆիկը համաչափ արտապատկերել օրդինատների առանցքի նկատմամբ:
Դիցուք, այս նկարում պատկերված է у=f(x) ֆունկցիայի գրաֆիկը:
Ոչ բացասական x-երի համար գրաֆիկը չենք փոփոխում, իսկ բացասական x-երի համար կառուցում ենք դրա համաչափ պատկերը օրդինատների առանցքի նկատմամբ:
Ստանում ենք у=f(|x|) ֆունկցիայի գրաֆիկը՝
у=f(|x|) ֆունկցիայի գրաֆիկը համաչափ է օրդինատների առանցքի նկատմամբ:
5. у = f(ax) ֆունկցիայի գրաֆիկը
у=f(ax) ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=f(ax) ֆունկցիայի գրաֆիկը, որտեղ a-ն դրական թիվ է, у=f(x) ֆունկցիայի գրաֆիկի միջոցով կառուցելիս տեղի է ունենում գրաֆիկի սեղմում կամ ձգում աբսցիսների առանցքի երկայնքով:
Գրաֆիկի սեղմումը կամ ձգումը տեղի է ունենում a թվի արժեքից կախված:
Եթե a1, ապա գրաֆիկը սեղմվում է աբսցիսների առանցքի երկայնքով՝ դեպի օրդինատների առանցքը: Եթե 0a, ապա գրաֆիկը ձգվում է աբսցիսների առանցքի երկայնքով՝ հեռանալով օրդինատների առանցքից:
Մասնավորապես՝
1) y=f(2x) ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը 2 անգամ սեղմել աբսցիսների առանցքի երկայնքով՝ դեպի օրդինատների առանցքը:
2) y=f(x/2) ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը 2 անգամ ձգել աբսցիսների առանցքի երկայնքով՝ հեռացնելով այն օրդինատների առանցքից:
6. у = af(x) ֆունկցիայի գրաֆիկը
у=af(x) ֆունկցիայի գրաֆիկի կառուցումը у=f(x) ֆունկցիայի գրաֆիկի միջոցով
у=af(x) ֆունկցիայի գրաֆիկը, որտեղ a-ն դրական թիվ է, у=f(x) ֆունկցիայի գրաֆիկի միջոցով կառուցելիս տեղի է ունենում գրաֆիկի սեղմում կամ ձգում օրդինատների առանցքի երկայնքով:
Գրաֆիկի սեղմումը կամ ձգումը տեղի է ունենում a թվի արժեքից կախված:
Եթե a1, ապա գրաֆիկը ձգվում է օրդինատների առանցքի երկայնքով՝ հեռացնելով այն աբսցիսների առանցքից: Եթե 0a, ապա գրաֆիկը սեղմվում է օրդինատների առանցքի երկայնքով՝ դեպի աբսցիսների առանցքը:
Մասնավորապես՝
1) y=3f(x) ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը 3 անգամ ձգել օրդինատների առանցքի երկայնքով՝ հեռացնելով այն աբսցիսների առանցքից:
2) y=f(x)/3 ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը 3 անգամ սեղմել օրդինատների առանցքի երկայնքով՝ դեպի աբսցիսների առանցքը:
7. у = f(x + a) ֆունկցիայի գրաֆիկի կառուցումը у = f(x) ֆունկցիայի գրաֆիկի միջոցով
у=f(x+a) ֆունկցիայի գրաֆիկի կառուցումը у=f(x)-ի գրաֆիկի միջոցով
Նույն կոորդինատային համակարգում կառուցենք y=x2 և y=(x+3)2: Առաջին ֆունկցիայի գրաֆիկը պարաբոլն է՝
| x | −3 | −2 | −4 | −5 | −1 | −6 | 0 |
| y | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
y=(x+3)2 ֆունկցիայի համար լրացնենք արժեքների աղյուսակը՝
Կոորդինատային հարթության վրա նշենք գտնված (−3;0), (−2;1), (−4;1), (−5;4), (−1;4), (−6;9), (0;9) կետերը և միացնենք դրանք կորով:
Կստանանք հետևյալ պարաբոլը՝
Համեմատենք y=x2 և y=(x+3)2 ֆունկցիաների գրաֆիկները:
Սա նույն y=x2 պարաբոլն է, որը x-երի առանցքով տեղաշարժված է 3 միավորով դեպի ձախ: Պարաբոլի գագաթը հիմա գտնվում է (−3;0) կետում, ոչ թե՝ (0;0) կետում, ինչպես y=x2 պարաբոլի դեպքում: Համաչափության առանցքը x=−3 ուղիղն է, ոչ թե y=x2 պարաբոլի x=0 առանցքը:
Իսկ եթե նույն կոորդինատային համակարգում կառուցենք y=x2 և y=(x−2)2 ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ երկրորդ գրաֆիկը ստացվում է առաջինի տեղաշարժով x-երի առանցքի ուղղությամբ՝ 2 միավորով դեպի աջ:
Նույն կերպ գրաֆիկները կառուցվում են նաև մյուս դեպքերում: Օրինակ՝ y=−2(x−4)2 ֆունկցիայի գրաֆիկը ստացվում է y=−2x2 պարաբոլի տեղաշարժով x-երի առանցքի ուղղությամբ՝ 4 միավորով դեպի աջ:
Ընդհանուր դեպքում ճիշտ է հետևյալ պնդումը՝
1) y=f(x+a), որտեղ a-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y=f(x) ֆունկցիայի գրաֆիկը x-երի առանցքի ուղղությամբ՝a միավորով դեպի ձախ:
2) y=f(x−a), որտեղa-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y=f(x) ֆունկցիայի գրաֆիկը x-երի առանցքի ուղղությամբ՝ a միավորով դեպի աջ:
9. у = f(x) + m ֆունկցիայի գրաֆիկի կառուցումը у = f(x) ֆունկցիայի գրաֆիկի միջոցով
Ինչպե՞ս կառուցել у=f(x)+m ֆունկցիայի գրաֆիկը, եթե տրված է у=f(x)-ի գրաֆիկը
Նույն կոորդինատային համակարգում կառուցենք y=x2 և y=x2+4 ֆունկցիաների գրաֆիկները: Կազմենք y=x2+4 ֆունկցիայի արժեքների աղյուսակը՝
| x | 0 | 1 | −1 | 2 | −2 |
| y | 4 | 5 | 5 | 8 | 8 |
Կոորդինատային հարթության վրա նշենք գտնված (0;4), (1;5), (−1;5), (2;8), (−2;8) կետերը և միացնենք դրանք կորով: Կստանանք պարաբոլ՝
Սա նույն y=x2 պարաբոլն է, որը y-երի առանցքով տեղաշարժված է 4 միավորով դեպի վերև: Պարաբոլի գագաթը հիմա գտնվում է (0;4) կետում, ոչ թե՝ (0;0) կետում, ինչպես y=x2 պարաբոլի դեպքում: Համաչափության առանցքը մնում է x=0 առանցքը, ինչպես և y=x2 դեպքում:
Իսկ եթե նույն կոորդինատային համակարգում կառուցենք y=x2 և y=x2−2 ֆունկցիաների գրաֆիկները, ապա կնկատենք, որ երկրորդ գրաֆիկը ստացվում է առաջինի տեղաշարժով y-երի առանցքի ուղղությամբ՝ 2 միավորով դեպի ներքև:
Նույն կերպ գրաֆիկները կառուցվում են նաև մյուս դեպքերում: Օրինակ՝ y=2x2−3 ֆունկցիայի գրաֆիկը ստացվում է y=2x2 պարաբոլի տեղաշարժով y-երի առանցքի ուղղությամբ՝ 3 միավորով դեպի ներքև:
Ընդհանուր դեպքում ճիշտ է հետևյալ պնդումը՝
1) y=f(x)+m, որտեղ m-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y=f(x) ֆունկցիայի գրաֆիկը y-երի առանցքի ուղղությամբ՝ m միավորով դեպի վերև:
2) y=f(x)−m, որտեղ m-ը տրված դրական թիվ է, ֆունկցիայի գրաֆիկը կառուցելու համար պետք է տեղաշարժել y=f(x) ֆունկցիայի գրաֆիկը y-երի առանցքի ուղղությամբ՝ m միավորով դեպի ներքև:
10. y=f(x+a)+m ֆունկցիայի գրաֆիկի կառուցումը
у=f(x+a)+m ֆունկցիայի գրաֆիկի կառուցումը у=f(x)-ի գրաֆիկի միջոցով
Կա у=f(x+a)+m ֆունկցիայի գրաֆիկը կառուցելու երկու եղանակ:
Առաջին եղանակ
1. Կառուցել y=f(x) ֆունկցիայի գրաֆիկը:
2. Տեղաշարժել y=f(x) ֆունկցիայի գրաֆիկը x-երի առանցքի ուղղությամբ |l| միավորով՝ դեպի ձախ, եթե l0 և դեպի աջ, եթե l:
3. Տեղաշարժել ստացված գրաֆիկը y-երի առանցքի ուղղությամբ |m| միավորով՝ դեպի վերև, եթե m0 և դեպի ներքև, եթե m:
Օրինակ
Կառուցենք y=(x−2)2−3 ֆունկցիայի գրաֆիկը:
Կառուցենք y=x2 ֆունկցիայի գրաֆիկը և այն տեղաշարժենք 2 միավորով դեպի աջ:
Կստանանք y=(x−2)2 ֆունկցիայի գրաֆիկը:
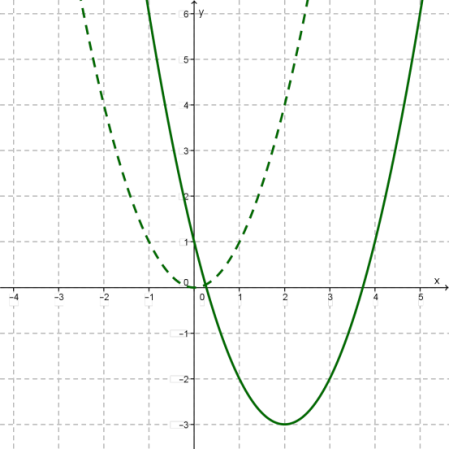
Տեղաշարժելով y=(x−2)2 պարաբոլը 3 միավորով դեպի ներքև` ստանում ենք y=(x−2)2−3 ֆունկցիայի գրաֆիկը:
Երկրորդ եղանակ
1. Տրված կոորդինատային համակարգում կառուցել նոր համակագ, որի առանցքներն են x=−a և y=m ուղիղները, իսկ սկզբնակետը (−l;m) կետն է:
2. Նոր համակարգում կառուցել y=f(x) ֆունկցիայի գրաֆիկը:
Օրինակ
Կառուցենք y=(x−2)2−3 ֆունկցիայի գրաֆիկը:
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
