(«Математика 6 класс» авторы: Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбург)
- применить формулу длины окружности для решения задач.
- воспитывать доброжелательное отношение друг к другу, развивать умение выслушать, понять.
циркуль, линейка, карандаш, ножницы, нитка, предметы круглой формы, карточки с заданиями.
- Практические (упражнения, практическая работа).
- воспитание качеств личности: толерантности, ответственности.
- развитие умений искать и выделять информацию в соответствии с поставленной целью;
- способствовать обогащению словарного запаса учащихся.
- формирование познавательной деятельности через практическую работу.
| № | Этапы урока Методы, реализуемые на этапе | Деятельность учителя | Деятельность ученика | УУД (с указанием вида: личностные, регулятивные, познавательные, коммуникативные) |
| 1 | Организационный момент. (1-2 мин.)
| Я рада вас всех видеть. | Класс готовится для работы, включаются в деловой ритм. | Оценивать ситуации взаимодействия в соответствии с правилами поведения и этики. (коммуникативные) |
| 2. | Целеполагание и мотивация. (3-5 мин)
Метод самоопределения в целях по аналогии с уже известным и усвоенным учащимися | Математика – наука древняя, интересная и полезная. Сегодня мы с вами в очередной раз убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие. А как сказал великий ученый, математик Лейбниц: “Кто хочет ограничиться настоящим, без знания прошлого, тот его никогда не поймёт…”, то и нам с вами для успешной работы нужно немного повторить. Вычислите: 2 ∙ 3,1; (6,2) 4 ∙ 3,12; (12,48) 6 ∙ 6,24 (37,44) Название нашей темы урока состоит из двух слов. Отгадайте загадку, и вы узнаете одно слово темы. Если видишь солнце в небе, или чашку с молоком, Видишь бублик или обруч, слышишь сказку с колобком, В круглом зеркале увидел ты сейчас свою наружность. И вдруг понял, что фигура называется окружность. А другое слово вы узнаете, выполнив самостоятельно первое задания на ваших карточках: Округлите число до заданного разряда, из предложенных вариантов выберете правильный ответ, каждому числу поставлена в соответствие буква, из букв вы составите слово. | ответ | буква |
| ответ | буква | | 3,142 | н | 3,2 | е | | 4 | м | 3,1415 | р | | 3,141 | т | 3,1416 | а | | 3 | д | 3,14 | и | | 3,15 | к | 3,1 | л | Округлите число 3,1415926 1 ЗАДАНИЕ: 1) до целых - _______ 2) до десятых - _______ 3) до сотых - _______ 4) до тысячных - _______ 5) до десятитысячных - _______ (длина) Итак, какая тема нашего урока? Правильно, тема нашего урока «Длина окружности» Откройте тетради, запишите число и тему урока: «Длина окружности» А сейчас мы с вами сформулируем цели нашего урока. Закончите предложения: Сегодня мы должны: Повторить…. (основные понятия темы «Окружность»). Узнать …… (как найти длину окружности). Закрепить ……. (применять новые знания при решении задач). | Слушают учителя.
Устно считают Отгадывают загадку
Индивидуально выполняют 1задание.
Формулируют тему урока. Записывают число и тему урока. Формулируют цели урока. | Осознание осваиваемого на уроке приема учебной деятельности, как ценности. (личностные)
Самооценка соответствия имеющихся знаний и умений заявленным требованиям (регулятивные)
Самоопределение в целях учебной деятельности (регулятивные) |
| 3. | Актуализация. (10 мин.)
Беседа с элементами игры
| Великий немецкий художник Альбрехт Дюрер мог одним движением руки нарисовать окружность почти идеально. Попробуйте нарисовать окружность подобно Дюреру. Что у вас получилось? А как правильно нарисовать окружность? (с помощью циркуля). Начертите окружность радиусом 2см. Мы увидели, как она выглядит, теперь вспомним понятия, связанные с окружностью, их изображение. Назовите как можно больше понятий, связанных с окружностью. Дети называют понятия, учитель вывешивает таблички на доску. Теперь посмотрите на таблицу и по группам заполните её. Здесь даны рисунки, к ним нужно подобрать и прикрепить понятия и определения, которые вывешены на другой доске. | Рисунок | Понятие | Определения | |  | Окружность- 1группа | «Все точки одинаково удалены от центра». 5 группа | | 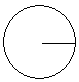 | Радиус- 2 группа | «Отрезок соединяет центр с точкой на окружности». 6 группа | | 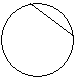 | Хорда- 3 группа | «Отрезок соединяет две точки окружности». 7 группа | | 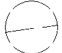 | Диаметр- 4 группа | «Отрезок соединяет две точки окружности и проходит через центр окружности». 8 группа | «Хорда, проходящая через центр окружности», «Замкнутая линия, все точки которой одинаково удалены от центра». Ребята, посмотрите на доске остались два определения, как вы думаете: к какому понятию можно отнести эти определения? | Рисуют окружность от руки. Делают вывод, что она нарисована неправильно. Рисуют окружность с помощью циркуля. Фронтальная работа. Называют понятия.
Читают понятия и определения. Заполняют таблицу. Работа в группах.
Фронтальная работа
Дополняют таблицу |
Знают понятия: - окружность - круг - радиус - хорда - диаметр Могут определить элементы окружности (предметные)
Самооценка соответствия имеющихся знаний и умений заявленным требованиям (регулятивные) |
| 4. | Изучение нового материала. (10 мин) Создание проблемной ситуации.
Исследовательское обучение (эксперимент), работа в группах
Репродуктивный метод
| А сейчас нам предстоит решить задачу нахождения длины окружности.
- Вспомните единицы измерения длины.
- С помощью какого инструмента можно измерять длину, например, длину отрезка? - Можно ли измерить длину нового забору вокруг нашей школы? - С помощью какого инструмента? - А можно ли измерить линейкой длину окружности? - Давайте подумаем, как можно измерить длину окружности?
(Испытывают затруднение, недостаточно знаний). Что именно вызывает затруднения? Не умеете находить длину окружности? Давайте научимся этому? - Выполним с вами следующую практическую работу. 2 ЗАДАНИЕ: Работать вы будете группами. На парте находятся модели окружности, вы берете модель, обвязываете её ниткой, распрямляете и измеряете длину нитки (т.е. измерьте длину окружности.) Затем вносите результат в таблицу в столбик длина окружности, затем линейкой измеряете диаметр и вносите значение в таблицу. Внимательно посмотрите на последнюю колонку и сделайте вывод: во сколько раз длина окружности больше диаметра с помощью калькулятора.
| Предмет | Длина окружности (С) | Длина диаметра (d) | С/d | | Стакан | | | | |
| | | |
Что у нас получилось? (Учитель выписывает несколько результатов на доске. Все они примерно одинаковы: С/d≈3,14.) Посмотрите, ребята, какие окружности у вас были разные, а отношения длин окружностей к их диаметрам какими получились? (получились одинаковые). Это характерно для всех окружностей? Какой вывод можно сделать?
Сейчас мы с вами пришли к такому же выводу, что и наши далекие предки много веков назад. Они заметили, что для того, чтобы сплести корзину нужной ширины, или, как мы теперь говорим диаметра, нужно было брать прутья примерно в три раза длиннее. Это было первое открытие, с тех пор прошло немало веков, прежде чем ученые доказали, что результат деления длины окружности на её диаметр постоянен и выражается не натуральным числом. А каким же? (бесконечным)
В 1706 году английский математик Уильямс Джонс для него ввел специальное обозначение  =3, 1415926... - это первая буква слова “периферия”, в переводе с греческого “окружность”. Необычность и удивительность этого числа в том, что его можно вычислять бесконечно и у него будет бесконечно знаков после запятой. Это, однако, не удерживает математиков от попыток вычислить как можно больше десятичных знаков числа пи. О нём говорят, как о неуловимом числе. =3, 1415926... - это первая буква слова “периферия”, в переводе с греческого “окружность”. Необычность и удивительность этого числа в том, что его можно вычислять бесконечно и у него будет бесконечно знаков после запятой. Это, однако, не удерживает математиков от попыток вычислить как можно больше десятичных знаков числа пи. О нём говорят, как о неуловимом числе. Для запоминания этих знаков есть стишок: Нужно только постараться И запомнить все как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Для обычных вычислений с числом π вполне достаточно запомнить два знака после запятой (3,14). Число π используется не только в математике, но и в физике. С этим предметом вам предстоит познакомиться на следующий год.
Если вы, ребята, округлили ваш результат, то ваш товарищ Даня, выполнял следующее задание: попробовал выполнить деление С=22 на d=7 до конца. И что же у тебя получилось, ученик записывает свой результат. Да, действительно, получается бесконечная десятичная дробь. К такому выводу пришел древнегреческий ученый Архимед. Это число называют архимедовым числом. |
Фронтальная работа. Отвечают на вопросы учителя.
Работа в группах. Выполняют практическую работу, заполняют таблицу в рабочих листах.
Фронтальная работа с классом. Отвечают на вопросы учителя. Формулирование вывода учащимися. (Какими бы различными ни были окружности, отношения их длин к диаметрам будут постоянно одинаковыми. Длина больше диаметра приблизительно в 3 раза.)
Происходит первичное осознание полученных результатов, а именно: отношение длины окружности к ее диаметру есть число постоянное. Первое знакомство с числом Пи. | Планирование своей деятельности для решения поставленной задачи (регулятивные). Анализ и синтез объектов, структурирование знаний, подведение под понятие, поиск и выделение необходимой информации на основе наблюдения и оценки выявленных закономерностей. (познавательные). Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог (коммуникативные). Проявление терпения и проявление доброжелательности и доверия к собеседнику, смыслообразование (личностные)
Число π. (предметные) |
| 4. | Физкультминутка. (1-2 минуты) | Ребята, сделаем разминку. Встаньте ровно. Покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим, что окружность превратилась в воздушный шарик и отпускаем ее. Молодцы! | Выполняют физкультминутку. | Контроль двигательной активности и эмоций (регулятивные) |
| 5. | Вывод формулы. (5 мин)
Аналитический метод | Вернемся к нашей проблеме нахождения длины окружности. - Можно ли измерить длину нового забору вокруг нашей школы? - С помощью какого инструмента? - Удобно ли делать такие большие измерения? - Как проще вычислить длину забора? (с помощью формулы) А сможете ли с помощью всё той же нитки найти длину любой окружности, например, круглой клумбы на даче или экватора Земли?
- Конечно же нет. Что же нужно сделать? (вывести формулу) А сможете ли с помощью всё той же нитки найти длину любой окружности. Конечно же нет.
Запишем в тетрадь: С – длина окружности, d – длина диаметра. Итак, мы имеем следующее соотношение: π = С / d Выведем из этой формулы формулу длины окружности С = d π или С = 2 Rπ. Эта формула называется формулой длины окружности. Чтобы найти длину окружности, надо знать её радиус или диаметр.
Решим задачу про вашу нарисованную в тетрадке окружность. r = 2см С = 2πr π = 3,14 С = 2*3,14*2= 12,56(см) С =? Ответ: длина окружности 12,56 см. | Находят решение для поставленного проблемного вопроса (с помощью формулы)
Делают записи в тетрадях | Совокупность умений по использованию математических знаний (познавательные)
Формулы длины окружности. (предметные) |
| 6. | Закрепление. (7 мин.)
Самостоятельная работа в группах с последующей проверкой у доски
Самостоятельная работа с взаимопроверкой по эталону
| Ребята, задачи по данной теме часто встречаются в экзаменах 9 и 11 класса. Сейчас мы с вами порешаем такие задачи по группам. Когда вы решите задачу, представитель группы выходит к доске и рассказывает это решение. 3 ЗАДАНИЕ: 3. задача: Диаметр долгоиграющей пластинки равен 50 см. Найдите длину окружности этой пластинки. Число π округлите до целого. (см. 1 задание) (С=3*50=150(см)=1,5(м)) 2. задача: Детская карусель, установленная в парке, имеет диаметр 3 м. за один сеанс карусель делает 2 оборота. Какое расстояние (в метрах) проезжает ребенок за один сеанс? (1) 3*3,14=9,42(м) –за 1 сеанс, 2) 9,42*2=18,84(м). Ответ 18,84 метра за 1 сеанс.) 1. задача: Военная машина ГАЗ 56 забуксовала, командир решил установить на колесо цепь в два ряда, чтобы машина могла выбраться из канавы. Хватит ли куска цепи длиною 5 метров, если известно, что диаметр колеса равен 70 см. (1) С= 3,14*0,7=2,198(м), 2) 2,198*2=4,396 (м). Ответ: Да)
А теперь для закрепления каждый самостоятельно решит тест в рабочем листе. 4 ЗАДАНИЕ: ТЕСТ Отрезок, соединяющий две точки окружности и проходящий через центр. А) радиус; Б) сторона; В) хорда; Г) диаметр. Число π равно А) 3,14; Б) 1,34; В) 3,91; Г) 4,13. Формула длины окружности А) С=πr Б) С=πd В) C=2πd Г) C=2r Чему равен диаметр окружности, радиус которой 3,8 см? А) 6,28 Б) 1,57 В) 7,6 Г) 3,14 5. Чему равен диаметр окружности, радиус которой 3,8 см? А) 6,28 Б) 1,57 В) 7,6 Г) 3,14 |
Работа в группах. Решают задачи. Один ученик из группы рассказывает свое решение у доски.
Индивидуально выполняют тест.
Взаимопроверка. ГАБВ | Моральная ответственность перед собой, коллективом и учителем (личностные)
Планирование своей деятельности для решения поставленной задачи, саморегуляция, самоконтроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив. (регулятивные) |
| 7.
| Задание на дом. (1 мин)
| Поскольку математика тесно связана с жизнью, с окружающей нас средой, в чем вы сегодня убедились, то и задание у вас будет творческое. Может вы увидите окружность в колесе, может в цирке, а у кого-то есть велосипед, у мамы на кухне кастрюли, кто-то крутит обруч, а кто-то любит искать города на глобусе. Придумайте практическую задачу на вычисление длины окружности и творчески оформите её для стенда интересных математических задач. |
|
|
| 8. | Подведение итогов. Рефлексия. (3 мин.) | Подведение итогов. А сейчас давайте вспомним, что сегодня на уроке мы: Повторили… (Что такое окружность, радиус, диаметр, как они связаны друг с другом). Узнали… (Формулы, по которым вычисляется длина окружности). Закрепили… (Научились применять эти формулы при решении задач)
Рефлексия. С помощью нарисованного вами смайлика оцените по пятибалльной системе | Отвечают на вопросы, поставленные на уроке. Учащиеся рисуют смайлики и высказывают свое мнение, ассоциации, мысли. | Умение слушать и вступать в диалог (коммуникативные) Уметь осуществлять самооценку на основе критерия успешности учебной деятельности. (личностные) |
















