Конспект урока математики по теме «Множество»
Класс:6
Технология: кейс-стади
Вид кейса – научно-исследовательский кейс
Урок по теме: «Множества. Решение задач».№3
Цели:
Образовательная: научить учащихся оперировать понятиями «множество», «элемент множества », «конечное, бесконечное, пустое множество», «круги Эйлера»
Деятельностная: научить учащихся решать задачи с помощью кругов Эйлера.
Цели
Повторить знания обучающихся о множестве;
Повторить понятие круги Эйлера;
Научить Формировать умения решать задачи на пересечение и объединение множеств.
Развивать умения анализировать, систематизировать, интерпретировать полученные результаты;
Планируемые результаты:
Предметные:
Базовый уровень:
А1. Знать определение понятия «множество»
А2. Знать понятия «пересечение» и «объединение», «круги Эйлера»
А3. Уметь пользоваться математической терминологией и символикой для совершения операций над множествами: пересечение, объединение.
А4. Уметь решать простейшие задачи с помощью кругов Эйлера.
Повышенный уровень
В1.Уметь решать задачи практической направленности.
В3. Уметь представлять решенную задачу по действиям в виде наглядной схемы.
Метапредметные результаты
Личностные: развитие познавательного интереса как основы мотивации учебной деятельности, осознавать важность и необходимость знаний для человека.
Универсальные учебные действия:
Регулятивные: осуществлять деятельность по реализации плана, соотносить результат своей деятельности с целью и оценивать свой результат, вносить коррективы и дополнения в способ своих действий.
Коммуникативные: уметь строить продуктивное взаимодействие, умение вступать в диалоги, участвовать в коллективном обсуждении проблемы.
Познавательные: преобразовать информацию и выбирать наиболее удобную для себя форму, представления информации; создавать и преобразовывать модели и схемы для решения задач; осуществлять выбор наиболее эффективных способов решения задач, в зависимости от конкретных условий; давать определения понятия. Тип урока: урок рефликсии, 3 урок.
ХОД УРОКА:
1.Этап мотивации (самоопределения).
Задача №1
Дан отрезок АВ длиной 4 см. Как найти множество точек, которые удалены от точки А на 3,2 см, а от точки В на 2,5 см.
-Где они будут находиться?
-Какой рисунок у вас получился?
-Ответ сформулируйте, используя понятие множество, пересечение множеств.
2.Этап актуализации и пробного учебного действия.
Ч
В
то показано на рис? Как называются такие круги?


А
•
4
•
•
•
3
2

•

•
•
С
Что обозначает эта схема?
- Леонард Эйлер предложил изображать множество кругами, а элементы множеств- точками внутри этих кругов.
Задача: Используя рис., ответьте на вопросы. Сколько элементов в множестве:
А,В,С;
А∩В
В∩С;
А∩С;
А∩В∩С;
А 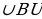 С ?
С ?
3.Этап локализации индивидуальных затруднений.
- Соедините концы отрезка АВ с полученными точками в задаче №1.
-Какие геометрические фигуры у вас получились, кроме окружностей?
-Чем являются отрезки, соединяющие концы отрезка АВ с полученными точками?(сторонами треугольника)
Учащиеся дополняют в тетради чертеж в задаче №1.
4.Этап построения проекта коррекции выявленных затруднений.
-Как построить треугольник с заданными сторонами?
-Чтобы найти ответ на поставленный вопрос, предлагаю перейти к работе с кейсом.
5. Этап реализации построенного проекта.
Парам предлагается рассмотреть решение готовой задачи, по аналогии с рассмотренной задачей решить еще одну задачу на построение, а затем решить ряд задач.
Для решения проблемы подготовлен кейс, в котором предложены информация по теме. Учащиеся должны ознакомиться с предложенной информацией и, опираясь на нее, решить данные задачи.
Учащимся выдается кейс.
Кейс
Содержание кейса
Обучающая задача.
К поиску пересечения множеств сводится решение некоторых геометрических задач. Рассмотрим, например, как построить треугольник АВС со сторонами АВ= 2,5 см, ВС= 3см, АС=2 см. Начертим сначала сторону АС (рис), а затем будем искать третью вершину треугольника- точку В.
Точка В должна находиться на расстоянии 2,5 см от точки А, т.е. быть элементом множества точек, удаленных на 2,5 см от точки А. Множество таких точек- это окружность с центром в точке А и радиуса 2,5 см.(см.рис.а).
С другой стороны, точка В должна отстоять на 3 см от точки С, т.е. принадлежать окружности с центром в точке С и радиусом 3 см (рис. б). Таким образом, точка В оказывается элементом сразу двух множеств точек окружностей. А значит она принадлежит их пересечению. Пересечение в данном случае содержит два элемента- точка В1 и В2 (см. рис.). Любую из этих точек можно взять за третью вершину треугольника. Остается соединить выбранную точку с точками А и С.
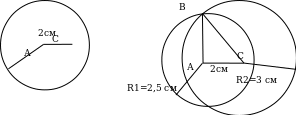
R1=2,5 см
а
б
Составьте алгоритм решения данной задачи.
Решите задачу самостоятельно по составленному алгоритму:
Задача(на построение треугольника по заданным сторонам)
Постройте треугольник со сторонами 3 см, 4см и 5 см на отдельных листах формата А-4 и объясните свое решение, используя термины «множество», «элементы множеств», «пересечение множеств».
Решите задачи, используя понятие объединение и пересечения множеств. При решении используйте круги Эйлера и символическую запись.
Задача 2. В математическом кружке занимается 17учеников класса (множество М), а в кружке «Умелые руки» занимается 18 учеников (множество К). Известно. Что каждый из учеников класса занимается хотя бы в одном из этих кружков, а 6 учеников посещают занятия обоих кружков.
Чем является объединение множеств М и К?
Сколько учеников в классе?
Задача 3. В 6 «В» классе учится 28 школьников. На родительское собрание пришли 24 мамы и 18 пап. Зная, что на собрание пришли родители всех учеников, определите, у скольких учеников на собрание пришли оба родителя.
Задача 4. Изобразите множества А, В и С кругами Эйлера и расставьте в них 7 точек так, чтобы:
В каждом множестве было по 4 элемента;
В каждом множестве было по 5элементов;
В множестве А и в множестве С было по 4 элемента, а в множестве В – 6 элементов.
Затем организуется работа в парах по поиску решения поставленной проблемы. Учитель консультирует учеников.
6.Этап обобщения затруднений во внешней речи.
Организуется обсуждение вариантов решений в парах.(обучающая задача из кейса)
7.Этап самостоятельной работы с самопроверкой по эталону.
Сравнение результатов работы с образцом, предложенном на слайде.(задача на построение треугольника по заданным сторонам)
8.Этап включения в систему знаний и повторения
Решение задач №2,3,4, из кейса. Выполняем проверку решения задач.
Задачи 3 и 4 проверяют, изображая решение кругами Эйлера на доске.
После работы с кейсом учащиеся сдают тетради на проверку.
9.Этап рефлексии учебной деятельности на уроке.
|
| ДА | НЕТ | Испытывал затруднения |
| Знаю как построить треугольник по трем сторонам |
|
|
|
| Могу построить треугольник по трем сторонам |
|
|
|
| Умею решать задачи на применение объединение и пересечение множеств |
|
|
|
| Умею применять символическую запись при решении задач |
|
|
|
Домашнее задание:
№ 356,357 (Г.К. Муравин, О.В. Муравина)









 С ?
С ?










