Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
| Тестовый балл | Школьная отметка |
| 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 1
Часть I
В1. Найдите значение выражения  log
log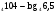
В2. Найдите остаток от деления многочлена  13
13  + 67
+ 67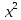 - 3x + 4 на многочлен P(x) =
- 3x + 4 на многочлен P(x) =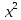 +5 x +1.
+5 x +1.
В3. На рисунке изображен график первообразной y = F (x) некоторой функции y = f(x), определенной на интервале ( - 16; - 2). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-15; -8]. 
В4. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
В5. Решите уравнение = 0,04.
= 0,04.
В6 Высота конуса равна 30, а длина образующей - 34. Найдите диаметр основания конуса.
В7. Коэффициент полезного действия некоторого двигателя определяется формулой  . При каком наименьшем значении температура нагревателя
. При каком наименьшем значении температура нагревателя  ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника
( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника  = 200 К?
= 200 К?
В8. Объем цилиндра равен 12см . Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
В9. Два автомобиля отправляются в 420 – километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найти скорость автомобиля, пришедшего к финишу вторым.
В10. Найдите наименьшее значение функции y = ( на отрезке [6; 8].
на отрезке [6; 8].
Часть II
С1. Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.
С2. Решите систему неравенств

.
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10 заданий. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
| Тестовый балл | Школьная отметка |
| 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 2
Часть I
В1. 
В2. Найдите остаток от деления многочлена 
 - 11
- 11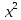 + x + 7 на многочлен P(x) =
+ x + 7 на многочлен P(x) = +3.
+3.
В3. На рисунке изображен график первообразной
некоторой функции y = f(x). Одна из первообразных этой функции равна F( x) =  . Найдите площадь заштрихованной фигуры.
. Найдите площадь заштрихованной фигуры.

В4. В фирме такси в данный момент свободно 10 машин: 5 черных, 1 желтая и 4 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
В5. Решите уравнение = 0,25.
= 0,25.
В6. В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.) Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
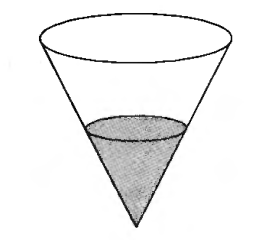 В7. Коэффициент полезного действия некоторого двигателя определяется формулой
В7. Коэффициент полезного действия некоторого двигателя определяется формулой  ,
,  - температура нагревателя ( в градусах Кельвина) ,
- температура нагревателя ( в градусах Кельвина) , - температура холодильника ( в градусах Кельвина) При какой температуре нагревателя
- температура холодильника ( в градусах Кельвина) При какой температуре нагревателя  КПД двигателя будет 45%, если температура холодильника
КПД двигателя будет 45%, если температура холодильника  = 275 К? Ответ выразите в градусах Кельвина.
= 275 К? Ответ выразите в градусах Кельвина.
В8. Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объем параллелепипеда.
В9. Из пункта А круговой трассы, длина которой равна 30 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого равна 92 км/ч, скорость второго — 77 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?
В10. Найдите набольшее значение функции y = ( на отрезке [19; 21].
на отрезке [19; 21].
Часть II
С1. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств
Итоговая контрольная работа
Структура контрольной работы
На выполнение контрольной работы по математике дается 2 часа. Работа состоит из двух частей. Первая часть содержит 10. К каждому заданию В1-В10 требуется дать краткий ответ. Задания С1, С2 выполняются на отдельном листе и ученик записывает подробное, обоснованное решение.
За выполнение каждого задания ученик получает определенное число баллов: задания В1 – В10 оцениваются в 1 балл, С1 – 2 балла, С2 – 3 балла.
Таблица перевода тестовых баллов в школьные отметки.
| Тестовый балл | Школьная отметка |
| 0-4 | 2 |
| 5-8 | 3 |
| 9-11 | 4 |
| 12-15 | 5 |
Вариант 3
Часть I
В1
В2. Найдите остаток от деления многочлена 
 + x на многочлен р(x) =
+ x на многочлен р(x) =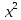 + x + 1
+ x + 1
В3. На рисунке изображен график некоторой функции у = Пользуясь рисунком, вычислите определенный интеграл
Пользуясь рисунком, вычислите определенный интеграл 
 dx
dx
В4. В сборнике билетов по биологии всего 25 билетов, в 12 из них встречается вопрос по круглым червям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику попадется вопрос по круглым червям.
В5. Решите уравнение  = 36.
= 36.
В6 Высота конуса равна 4, а длина образующей - 5. Найдите диаметр основания конуса.

В7. Температуру нагревательного элемента (в градусах Кельвина) в зависимости от времени (вминутах) можно вычислять по формуле Т(t) = Т0 + аt + b t2, где Т0 = 760 К, а = 34 К/мин, b = -0,2 К/мин2. Известно, что при температурах нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время (в минутах) после начала работы нужно отключать прибор.
В8. Площадь боковой поверхности цилиндра равна  , а высота — 8 . Найдите диаметр основания.
, а высота — 8 . Найдите диаметр основания.
В9. Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
В10. Найдите наимбольшее значение функции  на отрезке [-4,5; 0].
на отрезке [-4,5; 0].
Часть II
С1. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите угол между этой плоскостью и плоскостью основания цилиндра.
С2. Решите систему неравенств
.
ОТВЕТЫ
| Вариант | В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | В9 | В10 | С1 | С2 |
| 1 | 2 | -26х + 2 | 2 | 0,02 | -7 | 32 | 1000 | 4 | 60 | -5 | 15/4 | (0; 4) |
| 2 | 2 | - 0,5х+ 23,5 | 6 | 0,1 | 7 | 175 | 500 | 864 | 120 | -1 | 2 или 14 | (1; 3) |
| 3 | 2 | -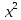 | 10 | 0,48 | 8 | 6 | 30 | 10 | 21 | 20 | arctg 3 или arctg 21/17 | 3 |







 log
log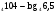
 13
13  + 67
+ 67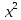 - 3x + 4 на многочлен P(x) =
- 3x + 4 на многочлен P(x) =
 = 0,04.
= 0,04.
 . При каком наименьшем значении температура нагревателя
. При каком наименьшем значении температура нагревателя  ( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника
( в градусах Кельвина) КПД этого двигателя будет не меньше 80%, если температура холодильника  = 200 К?
= 200 К? . Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр? на отрезке [6; 8].
на отрезке [6; 8].
 +3.
+3.  . Найдите площадь заштрихованной фигуры.
. Найдите площадь заштрихованной фигуры.
 = 0,25.
= 0,25.  В7. Коэффициент полезного действия некоторого двигателя определяется формулой
В7. Коэффициент полезного действия некоторого двигателя определяется формулой 









