Тесты и задания по теории вероятности
Вариант -1
| № | Задания | Варианты ответов |
|
| Задание на выбор единственного ответа заполните пропуск: |
|
|
1. | Если событие при заданных условиях может произойти или не произойти, то оно называется … | Случайным событием Результатом эксперимента Исходом Набором исходов |
| 2. | Если вероятность Р(А)=1, то событие называется… | Невозможным Достоверным Случайным Независимым |
| 3. | Если появление события В не изменяет вероятность события А, то события А и В называются… | Несовместными Независимыми Невозможными Достоверными |
| 4. | Случайная величина, которая может принять любое значение из заданного промежутка, называется… | Непрерывной Дискретной Счетной Измеряемой |
| 5. | Функция 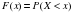 называется называется | Вероятностью Случайной функцией Функцией распределения Плотностью распределения |
| 6. | Дисперсия является характеристикой… | Расположения Рассеяния Формы распределения Симметрией |
| 7. | Все мыслимые объекты некоторого источника наблюдений называются… | Генеральной совокупностью Случайным коллективом Совокупностью объектов Множеством объектов |
| 8. | Выборка наблюдений, представленная в порядке возрастания, называется … | Упорядоченным рядом Вариационным рядом Упорядоченной выборкой Статистическим рядом |
| 9. | Количество наблюдений, попавших в заданный интервал интервальной таблицы, деленное на объем выборки, называется…
| Частотой Частостью Накопленной частостью Накопленной частотой |
| 10. | Оценка генерального параметра, полученная по выборке, является… величиной | Постоянной Случайной Независимой Определенной |
| 11. | Произведение всех натуральных чисел от 1 до n включительно называют…
| 1.медианой 2.дисперсией 3.факториалом 4.степень |
| 12. | Число размещений можно вычислить по формуле:
| 1. 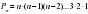 2. 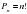 3. 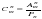 4. 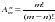
|
| 13. | Математическое ожидание вычисляется по формуле: | 1. 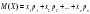 2. 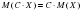 3. 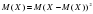 4. 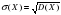 |
| 14. | Среднее квадратичное отклонение случайной величины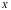 вычисляется по формуле: вычисляется по формуле: | 1. 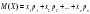 2. 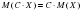 3. 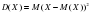 4. 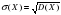 |
| 15. | Выбрать правильный ответ: Формула полной вероятности | 1. 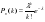 2. 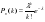 3.Р(А1)РА1(В)+ Р(А2)РА2(В)+…+ Р(Аn)РАn(В) 4. 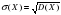 |
Задачи.
Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?
Задача 2. Найти математическое ожидание случайной величины X, если закон ее распределения задан таблицей:
| Х | 1 | 2 | 3 | 4 |
| р | 0,3 | 0,1 | 0,2 | 0,4 |
Задача 3. Задано распределение ДСВ Х
| 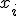
| -2 | -1 | 1 | 2 | 3 |
| 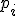
| 0,2 | 0,25 | 0,3 | 0,15 | 0,1 |
Построить ряд распределения случайных величин: 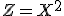
Задача 4. Найти математическое ожидание случайной величины 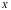 , зная закон ее распределения
, зная закон ее распределения
| 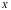
| -1 | 0 | 1 | 2 | 3 |
| 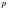
| 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Задача 5. Тест состоит из 10-ти вопросов, по 4 варианта ответа на каждый вопрос. Один ответ верный, остальные – нет. Какова вероятность случайно ответить верно ровно на 2 вопроса?
Тесты и задания по теории вероятности
Вариант -2
| № | Задания | Варианты ответов |
|
| Задание на выбор единственного ответа заполните пропуск: |
|
|
1. | Если случайные события А и В не могут появиться вместе, то они называются… | Независимыми Несовместными Противоположными Невозможными |
| 2. | Вероятность события А при условии, что произошло событие В называется… вероятностью | Безусловной Статистической Классической Условной |
| 3. | Случайная величина, которая принимает конечное или бесконечное счетное множество значений, называется… | Непрерывной Счетной Дискретной Бесконечной |
| 4. | Кривая, изображающая закон распределения для случайной переменной непрерывного типа, является графиком… | Вероятности Плотности распределения Функции распределения Распределения |
| 5. | Математическое ожидание является характеристикой… | Расположения Формы распределения Рассеяния Симметрией |
| 6. | Типичной характеристикой рассеяния случайной величины от ее математического ожидания является… | Размах Мода Стандартное отклонение Коэффициент асимметрии |
| 7. | Значения некоторого свойства, полученные на объектах выбранных из генеральной совокупности случайным образом, называются … | Выборкой Набором значений Совокупностью наблюдений Исходными данными |
| 8. | Количество наблюдений, попавших в заданный интервал интервальной таблицы, называется… | Частотой Частостью Относительной частотой Накопленной частотой |
| 9. | Наиболее часто встречающееся наблюдение в выборке называется … | Модой Медианой Коэффициентом асимметрии Средним арифметическим |
| 10. | Разделе математики, в котором решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств называется … | 1.Теорией вероятности 2.Комбинаторика 3.Математическая статистика 4.Стохастика
|
| 11. | Число перестановок можно вычислить по формуле:
| 1. 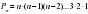 2.  3. 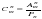 4. 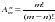
|
| 12 | Число сочетаний можно вычислить по формуле:
| 1. 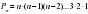 2.  3. 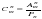 4. 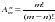
|
| 13. | Дисперсия дискретной случайной величины 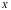 вычисляется по формуле: вычисляется по формуле: | 1.  2. 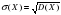 3. 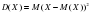 4.  |
| 14. | Выберите формулу Бернулли: | 1. 2. 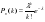 3.  4. 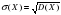 |
| 15. | Выбрать правильный ответ: 
| 1. 0 2. 1-P(A) 3. 1 4. P(A)+P(B)-P(AB) |
Задачи.
Задача 1. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?
Задача 2. Задано распределение ДСВ Х
| 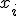
| -2 | -1 | 1 | 2 | 3 |
| 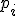
| 0,2 | 0,25 | 0,3 | 0,15 | 0,1 |
Построить ряд распределения случайных величин: 
Задача 3. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:
| X | 1 | 4 | 7 | 12 |
| р | 0,08 | 0,35 | 0,22 | 0,35 |
Задача 4. Найти дисперсию дискретной случайной величины X, заданной законом распределения:
| X | 3 | 5 | 8 | 11 |
| р | 0,16 | 0,18 | 0,51 | 0,15 |
Задача 5.Вероятность поразить мишень при одном выстреле равна 0,5. Найти вероятность поразить мишень ровно 50 раз, если сделано 100 выстрелов.
Тесты и задания по теории вероятности
Вариант -3
| № | Задания | Варианты ответов |
|
| Задание на выбор единственного ответа заполните пропуск: |
|
|
1. | Если случайные события А и В не могут появиться вместе, то они называются… | Независимыми Несовместными Противоположными Невозможными |
| 2. | Если вероятность Р(А)=1, то событие называется… | Невозможным Достоверным Случайным Независимым |
| 3. | Если появление события В не изменяет вероятность события А, то события А и В называются… | Несовместными Независимыми Невозможными Достоверными |
| 4. | Случайная величина, которая принимает конечное или бесконечное счетное множество значений, называется… | Непрерывной Счетной Дискретной Бесконечной |
| 5. | Кривая, изображающая закон распределения для случайной переменной непрерывного типа, является графиком… | Вероятности Плотности распределения Функции распределения Распределения |
| 6. | Функция 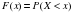 называется называется | Вероятностью Случайной функцией Функцией распределения Плотностью распределения |
| 7. | Дисперсия является характеристикой… | Расположения Рассеяния Формы распределения Симметрией |
| 8. | Типичной характеристикой рассеяния случайной величины от ее математического ожидания является… | Размах Мода Стандартное отклонение Коэффициент асимметрии |
| 9. | Значения некоторого свойства, полученные на объектах выбранных из генеральной совокупности случайным образом, называются … | Выборкой Набором значений Совокупностью наблюдений Исходными данными |
| 10. | Выборка наблюдений, представленная в порядке возрастания, называется … | Упорядоченным рядом Вариационным рядом Упорядоченной выборкой Статистическим рядом |
| 11. | Количество наблюдений, попавших в заданный интервал интервальной таблицы, деленное на объем выборки, называется…
| Частотой Частостью Накопленной частостью Накопленной частотой |
| 12. | Наиболее часто встречающееся наблюдение в выборке называется … | Модой Медианой Коэффициентом асимметрии Средним арифметическим |
| 13. | Разделе математики, в котором решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств называется … | 1.Теорией вероятности 2.Комбинаторика 3.Математическая статистика 4.Стохастика
|
| 14. | Произведение всех натуральных чисел от 1 до n включительно называют…
| 1.медианой 2.дисперсией 3.факториалом 4.степень |
| 15. | Число размещений можно вычислить по формуле:
| 1. 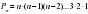 2. 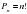 3. 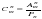 4. 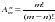
|
Задачи.
Задача 1. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?
Задача 2. Разыгрываются две вещи стоимостью по 5000 руб и одна вещь стоимостью 30000 руб. Составить закон распределения выигрышей для человека, купившего один билет из 50.
Задача 3. Заданы распределения двух независимых случайных величин X и Y:
| 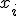
| 0 | 1 | 2 |
| 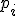
| 0,2 | 0,4 | 0,4 |
| 
| 2 | 3 | 4 |
| 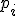
| 0,3 | 0,3 | 0,4 |
Найти: ряд распределения случайных величин  ;
;
Задача 4. Вычислить дисперсии и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения.
| Х | 4,3 | 5,1 | 10,6 |
| р | 0,2 | 0,3 | 0,5 |
Задача 5. В среднем 80 % студентов группы сдают зачет с первого раза. Тогда вероятность того, что из 6 человек, сдавших зачет, с первого раза сдадут ровно 4 студента.
Тесты и задания по теории вероятности
Вариант -4
| № | Задания | Варианты ответов |
|
| Задание на выбор единственного ответа заполните пропуск: |
|
|
1. | Если событие при заданных условиях может произойти или не произойти, то оно называется … | Случайным событием Результатом эксперимента Исходом Набором исходов |
| 2. | Вероятность события А при условии, что произошло событие В называется… вероятностью | Безусловной Статистической Классической Условной |
| 3. | Если появление события В не изменяет вероятность события А, то события А и В называются… | Несовместными Независимыми Невозможными Достоверными |
| 4. | Случайная величина, которая принимает конечное или бесконечное счетное множество значений, называется… | Непрерывной Счетной Дискретной Бесконечной |
| 5. | Случайная величина, которая может принять любое значение из заданного промежутка, называется… | Непрерывной Дискретной Счетной Измеряемой |
| 6. | Кривая, изображающая закон распределения для случайной переменной непрерывного типа, является графиком… | Вероятности Плотности распределения Функции распределения Распределения |
| 7. | Функция 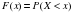 называется называется | Вероятностью Случайной функцией Функцией распределения Плотностью распределения |
| 8. | Математическое ожидание является характеристикой… | Расположения Формы распределения Рассеяния Симметрией |
| 9. | Типичной характеристикой рассеяния случайной величины от ее математического ожидания является… | Размах Мода Стандартное отклонение Коэффициент асимметрии |
| 10. | Все мыслимые объекты некоторого источника наблюдений называются… | Генеральной совокупностью Случайным коллективом Совокупностью объектов Множеством объектов |
| 11. | Выборка наблюдений, представленная в порядке возрастания, называется … | Упорядоченным рядом Вариационным рядом Упорядоченной выборкой Статистическим рядом |
| 12. | Оценка генерального параметра, полученная по выборке, является… величиной | Постоянной Случайной Независимой Определенной |
| 13. | Разделе математики, в котором решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств называется … | 1.Теорией вероятности 2.Комбинаторика 3.Математическая статистика 4.Стохастика
|
| 14. | Математическое ожидание вычисляется по формуле: | 1. 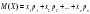 2. 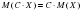 3. 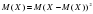 4. 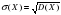 |
| 15. | Выберите формулу Бернулли: | 1. 2. 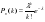 3.  4. 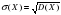 |
Задачи.
Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.
Задача 2. Даны вероятности значений случайной величины 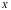 : значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины
: значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины 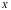 .
.
Задача 3. Заданы распределения двух независимых случайных величин X и Y:
| 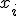
| 0 | 1 | 2 |
| 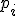
| 0,2 | 0,4 | 0,4 |
| 
| 2 | 3 | 4 |
| 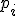
| 0,3 | 0,3 | 0,4 |
Найти: ряд распределения случайных величин  ;
;
Задача 4. Дискретные независимые случайные величины заданы законами распределения:
| Х | 1 | 3 | 7 | 9 |
| р | 0,3 | 0,1 | 0,2 | 0,4 |
Найти математическое ожидание и дисперсию.
Задача 5. Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна?







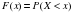 называется
называется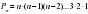
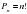
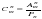
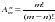
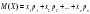
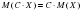
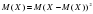
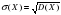
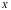 вычисляется по формуле:
вычисляется по формуле: