Упрощение логических функций двух переменных методом карт карно

Н.Н. Моисеева

Государственное бюджетное образовательное учреждение «Школа № 1432»

УПРОЩЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ МЕТОДОМ КАРТ КАРНО

Аннотация

Предлагаемая авторская разработка может дополнить чебный материал при изучении темы «Основы математической логики» по предмету информатика, математика, а также в проектной и исследовательской деятельности обучающихся.

Актуальность данной работы состоит в понимании механизмов преобразования логических выражений, представления сложных логических функций (штрих Шеффера, стрелка Пирса, импликации и т.п.) через базовые логические функции И, ИЛИ, НЕ методом карт Карно.

Ключевые слова: логика, логические выражения, логические функции, инверсия, конъюнкция, дизъюнкция, методы минимизации, метод карт Карно.

Контактная информация

Моисеева Надежда Николаевна, учитель информатики и ИКТ, Государственное бюджетное образовательное учреждение «Школа № 1432», 119634 г. Москва ул. Шолохова д. 19, телефон 8(495)7327460, e-mail: [email protected]

N.N. Moiseevа

State educational institution "School № 1432"

SIMPLIFYING BOOLEAN FUNCTIONS OF TWO VARIABLES BY METHOD OF CARDS OF KARNO

Abstract

The proposed authoring can complement the learning material under the topic "foundations of mathematical logic" on the subject of computer science, mathematics, as well as in project and research activities of students.

The relevance of this work lies in understanding the mechanisms of transformation of logical expressions that represent complex logical functions (Sheffer's stroke, arrow Pier, implications, etc.) using basic logic functions AND, OR, NOT by a method of cards of Carnot.

Keywords: logic, logical expression, logical functions, inverse, conjunction, disjunction, methods of minimization, a method of cards of Carnot.

Обучаем по-новому

В соответствии с требованиями ФГОС для развития потенциала одаренных и талантливых детей с участием самих обучающихся формируется индивидуальная траектория развития обучающегося. Предлагаемая авторская разработка может дополнить учебный материал при изучении темы «Основы математической логики» по предмету информатика, математика, а также в проектной и исследовательской деятельности обучающихся.

В настоящее время очевидна роль информатики в формировании современной научной картины мира, фундаментальный характер ее основных понятий, законов, всеобщность ее методологии.

Современные направления создания и использования информационной образовательной среды (ИОС) школы предоставляют множество новых возможностей в развитии авторских методик обучения.

Развитие ИКТ компетентности ребёнка - это приобретение опыта создания, преобразования, представления, хранения информационных объектов, умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.

Изучение основ логики имеет прикладное значение и используется для более полного представления о принципах действия современной компьютерной техники, а также при изучении программирования.

Почему надо научить ребят пониманию основ логики?

Развитие мышления школьников всегда было одной из задач обучения. Истина и логика взаимосвязаны, поэтому теоретическое и практическое значение логики невозможно переоценить. Научиться правильно, рассуждать, мыслить и познавать окружающий мир помогает одна из величайших наук – Логика. Наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью языка. Так как мышление оформляется на языке в виде рассуждения, то можно сказать, что логика - это наука о способах доказательств и опровержений.

Исторически логика изучалась как часть философии. Сейчас логика изучается как часть математики и информатики.

Предметом авторской разработки является представление логических функций двух переменных через набор базовых логических функций, практическая проверка тезиса о представимости любой логической функции через базовые.

Актуальность данной работы состоит в понимании механизмов преобразования логических выражений, представления сложных логических функций (штрих Шеффера, стрелка Пирса, импликации и т.п.) через базовые логические функции И, ИЛИ, НЕ. Приобретённые навыки позволяют глубже понять логические основы устройства компьютера и успешно освоить программирование.

В результате применения описанного метода упрощения (минимизации) можно проследить классификацию всех логических функций одной и двух переменных. Для каждой функции может быть получено их оптимальное представление через базовые функции И, ИЛИ, НЕ с помощью карт Карно.

Основоположники логики

«Воспитание нуждается в трех вещах: в даровании, науке, упражнении.»

Аристотель

Древнегреческий философ и учёный Аристотель является и основоположником логики. Познание у Аристотеля имеет своим предметом бытие. Основа опыта — в ощущениях, памяти и привычке. Любое знание начинается с ощущений: оно есть то, что способно принимать форму чувственно воспринимаемых предметов без их материи; разум же усматривает общее в единичном.

Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике, который сохраняет своё непреходящее значение и поныне. Он разработал теорию мышления и его формы, понятия, суждения и умозаключения.

В 1666 в Лейпциге Лейбниц пишет габилитационную работу по философии «О комбинаторном искусстве», в которой высказывается идея создания математической логики. Из божественного попечительства над миром философ выводит универсальную, неразрывную связь всего со всем. Одно тело не отделено от остальных. Оно – кирпичик в едином здании мира. «Я стою на том, что плохая голова, обладая вспомогательными преимуществами и упражняя их, может перещеголять самую лучшую, подобно тому, как ребенок может провести по линейке линию лучше, чем величайший мастер от руки».

Английский математик и логик. Буль был, обратившимся к логической проблематике. Идеи применения символического метода к логике впервые высказаны им в статье «Математический анализ логики».

Буль высказывал пожелание, чтобы о его взглядах судили по обширному трактату «Исследование законов мышления, на которых основываются математические теории логики и вероятностей». Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. 

Единицей Буль обозначал универсум мыслимых объектов, буквенными символами — выборки из него, связанные с обычными прилагательными и существительными. Буль показал, что символика такого рода подчиняется тем же законам, что и алгебраическая, из чего следовало, что их можно складывать, вычитать, умножать и даже делить. Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций. 

Аристотель, Джордж Буль и Лейбниц познакомили нас с наукой о формах, методах и законах интеллектуальной познавательной деятельности - с логикой.

Логические функции

В логике известны три базовые логические операции, выражаемые с помощью логических связок И, ИЛИ, НЕ (конъюнкция, дизъюнкция и отрицание).

Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

  Логический элемент — это устройство, реализующее ту или иную логическую функцию. Y=f(X1,X2,X3,...,Xn) — логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

Логические функции одной переменной

Таблица истинности функции одной переменной Y=f(X) содержит всего 2 строки, а число функций одной переменной равно 4.

Функция константа 0, Y=0. Техническая реализация этой функции — соединение вывода Y с общей шиной с нулевым потенциалом. Таблица истинности функции константа 0 имеет вид:

 

Функция Y=f(X)=X — функция повторения. Техническая реализация этой функции - соединение между собой выводов X и Y.

Таблица истинности функции повторения имеет вид:

 

Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X). Техническая реализация этой функции - инвертор на любом транзисторе или логическом элементе, или транзисторный ключ.

Таблица истинности функции отрицания имеет вид:

 

Функция константа 1, Y=1. Техническая реализация этой функции — соединение вывода Y с источником питания.

Таблица истинности функции константа 1 имеет вид:

 

Важнейшей функцией одной переменной является отрицание НЕ, остальные функции являются тривиальными.

Логические функции двух переменных

Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4 строки, а число функций двух переменных равно 16.

Рассмотрим только несколько основных функций двух переменных.

Логическое ИЛИ (логическое сложение, дизъюнкция):

Y= X1 + X2 = X1VX2

Техническая реализация этой функции — два параллельно соединенных ключа:

 

Таблица истинности логического ИЛИ имеет вид:

 

Логический элемент ИЛИ обозначается на схемах следующим образом:

 

Логическое И (логическое умножение, конъюнкция, схема совпадений): Y = X1X2 = X1&X2

Техническая реализация этой функции — два последовательно соединенных ключа:

 

Таблица истинности логического И имеет вид:

 

Логический элемент И обозначается на схемах следующим образом:

 

Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид:

 

Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:

 

Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)

Таблица истинности функции И-НЕ имеет вид:

 

Логический элемент И-НЕ обозначается на схемах следующим образом:

 

Есть ещё три логические функции двух переменных, имеющие специальные названия: импликация, эквивалентность, неравнозначность (исключающее ИЛИ, сложение по модулю 2). Последние две функции являются взаимно обратными, также как, например, функция И и функция штрих Шеффера.

Число строк в таблице — это число возможных наборов значений аргументов. Оно равно 2n, где n — число переменных. Число различных функций n переменных равно 2^2n.

Представление логических функций через И, ИЛИ, НЕ

Теорема 1

Любая функция двух переменных может быть представлена в виде комбинации функций И, ИЛИ, НЕ.

Доказательство

Таблица истинности любой функции имеет вид:

Где Y0, Y1, Y2, Y3 принимают значения 0 или 1. Составим конъюнкцию (ИЛИ) из всех строк, где Yi равно 1. Каждый элемент конъюнкции это дизъюнкция (И) переменных, если Xi = 1 в соответствующей строке или их отрицание, если Xi = 0 в соответствующей строке. Очевидно, что данный элемент конъюнкции равен 1 только для этой строки и 0 для всех остальных.

Тогда, конъюнкция будет равна 1 только для Yi = 1 и 0 во всех остальных случаях. То есть данная конъюнкция будет равна исходной функции. Таким образом, исходная функция представляется через И, ИЛИ, НЕ, что и требовалось доказать.

Пример

Представим через И, ИЛИ, НЕ функцию эквивалентности. Таблица истинности функции имеет вид

Y = X1X2  X1X2

Через функции И, ИЛИ, НЕ логические функции могут быть представлены несколькими способами. Поэтому целесообразно минимизировать представление функций с использованием наименьшего количества базовых функций. Для этого служат карты Карно.

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 ... XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 ... XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

Упрощение представления функций

Карты Карно

Через функции И, ИЛИ, НЕ логические функции могут быть представлены несколькими способами. Поэтому целесообразно оптимизировать представление функций с использованием наименьшего количества базовых функций. Для минимизации функций алгебры логики был разработан ряд методов:

1. метод непосредственных преобразований логических функций;

2. метод минимизации логических функций при помощи карт Карно;

3. метод Квайна-Мак-Класки;

4. метод Блейка-Порецкого;

5. метод Петрика и другие.

Метод непосредственных преобразований логических функций с использованием законов логики обычно подробно разбирается в процессе изучения темы. Поэтому, остановимся более подробно на методе минимизации логических функций при помощи карт Карно.

Карта Карно – это графический способ минимизации (упрощения) логических функций и представляет собой операции попарного склеивание и элементарного поглощения. Карта Карно рассматривается как перестроенная соответствующим образом таблица истинности функции.

Карты Карно были изобретены в 1952 году Эдвардом В. Вейчем и усовершенствованы в 1953 году физиком Морисом Карно.

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 ... XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 ... XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

Принципы склейки:

• Склейку клеток карты Карно можно осуществлять по единицам

• Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.

• Область, которая подвергается склейке, должна содержать только единицы (нули).

• Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники. Все единицы (нули) должны попасть в какую-либо область.

• С точки зрения минимальности число областей должно быть как можно меньше.

• Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:

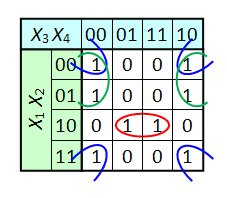
Минимизация логических функций двух переменных

1. Конъюнкция

X1 X2

1. Запрет по Х1

X1 X2

1. Повторение X1

X1

1. Запрет по Х2

X1 X2

1. Повторение X2

X2

1. Сложение по модулю 2

X1X2 или X2 X1

1. Дизъюнкция

X1 или X2

1. Стрелка Пирса

X1X2

Таким образом, соседние клетки карты Карно можно группировать для исключения переменной. Число группируемых клеток может быть и больше двух, но их число должно быть четным и они должны соприкасаться (являться соседними) друг с другом.

Допускается также иметь несколько групп перекрывающихся клеток, как в только что рассмотренном примере.

Группироваться могут также клетки первой и последней строк, первого и последнего столбцов, т. е. карту допускается сворачивать в цилиндр, как по вертикальной, так и по горизонтальной оси.

Рассмотрим несколько теорем, доказывающих что любая функция представима через И, ИЛИ, НЕ.

Представление логических функций через базовые функции

Функции И, ИЛИ, НЕ не являются единственным набором базовых функции. Существую ещё несколько наборов базовых функций, представляющих все другие функции.

Проверить является ли набор функций базовым можно на основе следующей теоремы.

Теорема 2

Для того, чтобы набор функций был базовым, то есть представлял все другие функции, достаточно чтобы через этот набор можно было представить функции И, ИЛИ, НЕ.

Доказательство

Любая функция представима через И, ИЛИ, НЕ. Заменим в этом представлении данные функции их эквивалентом через другой базовый набор. Тогда исходная функция представляется через данный базовый набор, что и требовалось доказать.

Представление логических функций через штрих Шеффера

Теорема 3

Через функцию штрих Шеффера Y = X1|X2 =  (X1X2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция штрих Шеффера была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =(Х11) = Х1|1

Конъюнкция Х1 Х2 = ((Х1 Х2)) = (X1|X2) = (X1|X2) |1

Дизъюнкция Х1Х2 = (Х1Х2) = Х1|Х2 = (Х1|1)|(Х2|1)

Теорема доказана.

Представление логических функций через стрелку Пирса

Теорема 4

Через функцию стрелка Пирса Y = X1X2 =  (X1X2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция стрелка Пирса была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =(Х10) = Х10

Конъюнкция Х1 Х2 = (Х1 Х2) = (X1X2)=(X10)(X20)

Дизъюнкция Х1Х2 = ((Х1Х2)) = (Х1Х2) = (Х1Х2)0

Теорема доказана.

Представление логических функций через импликацию

Теорема 5

Через функцию импликация Y = X1X2 =  X1X2 можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция импликации была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =Х11 = Х11

Конъюнкция Х1 Х2 = (Х1 Х2) =  (X1X2)=(X1X2) 1

=( X1(X21) 1

Дизъюнкция Х1Х2 = (Х1)Х2 = (Х1) Х2 = (Х11)Х2

Теорема доказана.

Позитивный заключительный аккорд

Теория логических функций прошла долгую историю от Аристотеля до наших дней. В современном виде её сформулировал Джорж Буль.

Логические функции являются математической основой современных вычислительных устройств. Для реализации логических функций в вычислительных устройствах важно унифицировать и минимизировать их представление.

Таким образом, набор функций, через которые можно выразить любые другие функции, называется полным набором базовых функций, т.е. конъюнкция, дизъюнкция и отрицание является полным набором. Упрощение логических выражений можно произвести с помощью методов минимизации. Для несложных функций используются алгебраические преобразования. Для более сложных с числом переменных от 2 до 6 применяют карты Карно.

Понимание методов преобразования позволяют глубже понять логические основы устройства компьютера и успешно освоить программирование.

Список литературных и интернет-источников:

1. А.А. Ивин Логика, учебное пособие издание 2 Москва, Знание 1998

2. Государственные образовательные стандарты общего образования http://www.edu.ru/db/portal/obschee/

3. Д.А. Владимиров Булевы алгебры Москва, Наука 1969

4. Википедия свободная энциклопедия, Логика http://ru.wikipedia.org/

5. Высказывания, цитаты и афоризмы великих людей
   Источник: http://www.wisdoms.ru/pavt/p123.html

6. Н.Н. Моисеева Методические разработки, учебный сайт http://www.schools.keldysh.ru/sch1019/

7. Н.Н. Моисеева Минимизация логических функций двух переменных http://www.rusnauka.com/1_NIO_2014/Matemathics.htm

17