Тема урока: Урок – практикум по решению задач ОГЭ модуля «Геометрия».
9класс
Тип урока: урок систематизации и обобщения знаний и умений.
Цели урока:
- повторить и обобщить знания по теории геометрии,
- продолжить работу по решению геометрических задач при подготовке к ГИА
Задачи урока:
Образовательные:
повторить теоретические знания по темам «Четырёхугольники», «Площадь»;
продолжить работу по подготовке к ГИА;
проверка знаний и их коррекция.
Развивающие:
развитие внимания, мышления, наблюдательности, активности;
развитие математической речи;
развитие умений анализировать свои ошибки;
развитие умений применять полученные знания на практике.
Воспитательные:
воспитывать дисциплинированность, высокую работоспособность и организованность;
воспитание познавательной активности, культуры общения, ответственности;
привить навыки самостоятельной работы;
воспитывать умение проводить оценку и самооценку знаний и умений.
Оборудование: компьютер, проектор, презентация для сопровождения урока, раздаточный материал.
Планируемые результаты:
Личностные:
- Осознание обучающимися ценности полученных знаний .
- Умение провести самооценку.
- Ценностное отношение к умению удерживать учебную задачу.
- Формирование этических норм поведения, уважение к труду.
Метапредметные:
- Умение принимать и сохранять цель урока.
- Умение находить способы решения поставленной цели.
- Умение планировать, контролировать и оценивать свои действия.
- Умение слушать собеседника и вести диалог, высказывать свою
точку зрения, правильно говорить.
- Умение провести рефлексию своих действий на уроке.
Предметные:
- Формирование навыка решения практических задач по геометрии.
- Применение знаний по теории геометрии к решению геометрических задач.
- Умение работать с математическим текстом, использовать понятийный аппарат, давать определения, выделять главное, систематизировать и обобщать, сравнивать.
Тип урока: урок совершенствования знаний, умений и навыков учащихся.
Технологии: ИКТ - технология, технология критического мышления, здоровьесберегающая технология. Методы: метод дифференцированного обучения, метод групповой работы, метод математического моделирования, метод научности Форма: урок - практикум
Оборудование: проектор, презентация, карточки, заготовки для рефлексии.
Структура урока
1. Организационный момент, мотивация учащихся. Определение темы урока -3 мин.
2. Актуализация знаний -15 мин.
1) устная работа по теории;
2) Тренировочные упражнения с последующей проверкой по слайду
3) работа в группах, с дальнейшей проверкой у доски .
3. Физкультминутка-1 мин.
4.Обобщение и систематизация знаний и умений учащихся.-5мин 5. Домашнее задание -1 мин.
6. Самостоятельная работа по вариантам с последующей проверкой и коррекционной работой -15 мин.
7. Итог урок. Оценка работы учащихся. Рефлексия -5 мин.
Ход урока.
Организационный этап.
Приветствие учащихся.
Здравствуйте, ребята! Улыбнулись друг другу. Присаживайтесь.
Восточная мудрость гласит:
«Приобретать знания – это храбрость, приумножать знания – это мудрость, а умело применять – великое искусство» (Слайд 1)
Подготовительная работа.
Сегодня нам на уроке будет необходимо трудолюбие и терпение, внимание, как, впрочем, и на каждом уроке. А знаете ли вы, какие разделы математики нам предлагается решать на экзамене ОГЭ? Учащиеся отвечают - модуль «Алгебра», модуль «Геометрия». А вот какому модулю мы сегодня посвятим наш урок, вы узнаете, отгадав ребус.
(слайд 2 )
 Ребус (геометрия)
Ребус (геометрия)
- Правильно, ребята! Геометрия. А вы мне можете сказать, почему именно «геометрия», и какие задания нам предлагается решить в модуле геометрия? (Учащиеся отвечают) (Нам надо научиться хорошо решать геометрические задачи… )
- А теперь давайте озвучим тему нашего урока: ( дети называют тему) (Слайд3)
III .Актуализация знаний учащихся
1) Повторение теоретического материала.
Выбрать верные утверждения из списка и отметить их. Такое задание № 19 в КИМах ОГЭ, если вы помните.
(Приложение 1)
Вертикальные углы равны.
Сумма двух смежных углов равна 180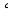 .
.
Сумма вертикальных углов равна 180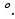
Если две стороны и угол одного треугольника соответсвенно равны двум сторонам и углу другого треугольника,то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответсвенно равны двум сторонам и углу между ними другого треугольника,то такие треугольники равны.
В треугольнике против меньшего угла лежит меньшая сторона.
Длина окружности радиуса 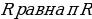 .
.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
Треугольник АВС, у которого АВ= 3,ВС=4, АС=5,является тупоугольным.
Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Проверка:
- Назовите выбранные утверждения. ( ученики называют по одному верному утверждению) Учитель выводит на слайд верные утверждения.
Верные утверждения: ( слайд 4 )
Вертикальные углы равны.
Сумма двух смежных углов равна 180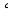 .
.
Если две стороны и угол между ними одного треугольника соответсвенно равны двум сторонам и углумежду ними другого треугольника,то такие треугольники равны.
В треугольнике против меньшего угла лежит меньшая сторона.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
10. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
11.В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Молодцы!
Оценочные листы:
4 утверждения – «3»;
5 утверждений – «4»
6 утверждений – «5»
2) Вспомнить и записать формулы площадей фигур на плоскости ( работают на листочках)
Приложение 2
| № | Название фигур | Формулы для вычисления площади фигур планиметрии | Фигуры планиметрии |
| 1 | Прямоугольник |
| 
|
| 2 | Квадрат |
| 
|
| 3 | Треугольник |
|  |
| 4 | Прямоугольный треугольник |
| 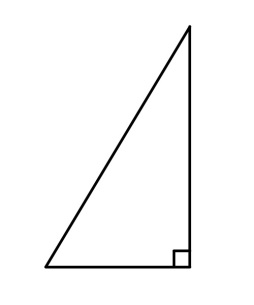
|
| 5 | Параллелограмм |
| 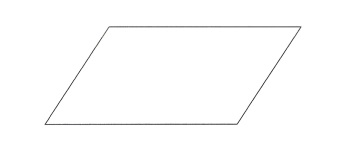
|
| 6 | Трапеция |
| 
|
| 7 | Ромб |
| 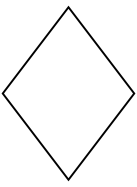
|
| 8 | Круг |
| 
|
Проверка:
Пройти и посмотреть, сколько формул записали учащиеся.
Вывести на слайд все формулы (слайд 5 )
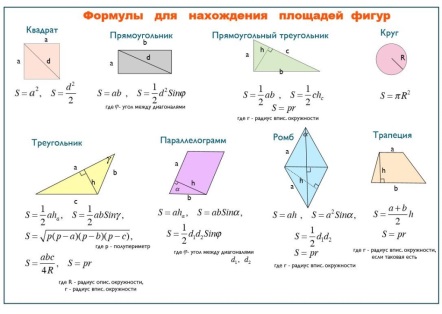
А теперь подумайте каждый, сколько он формул вспомнил и поставьте оценку в оценочный лист:
за 4-5 формул – «3»;
за 6-7 формул – «4»;
за 8 формул – «5»
3) Тренировочные упражнения с последующей проверкой по слайду.
Приложение 3.
- Вычислим, площади плоских фигур: 5 мин
По одному учащемуся выходят к доске записывают и комментируют решения и ответы.
(слайд 6 )
1. 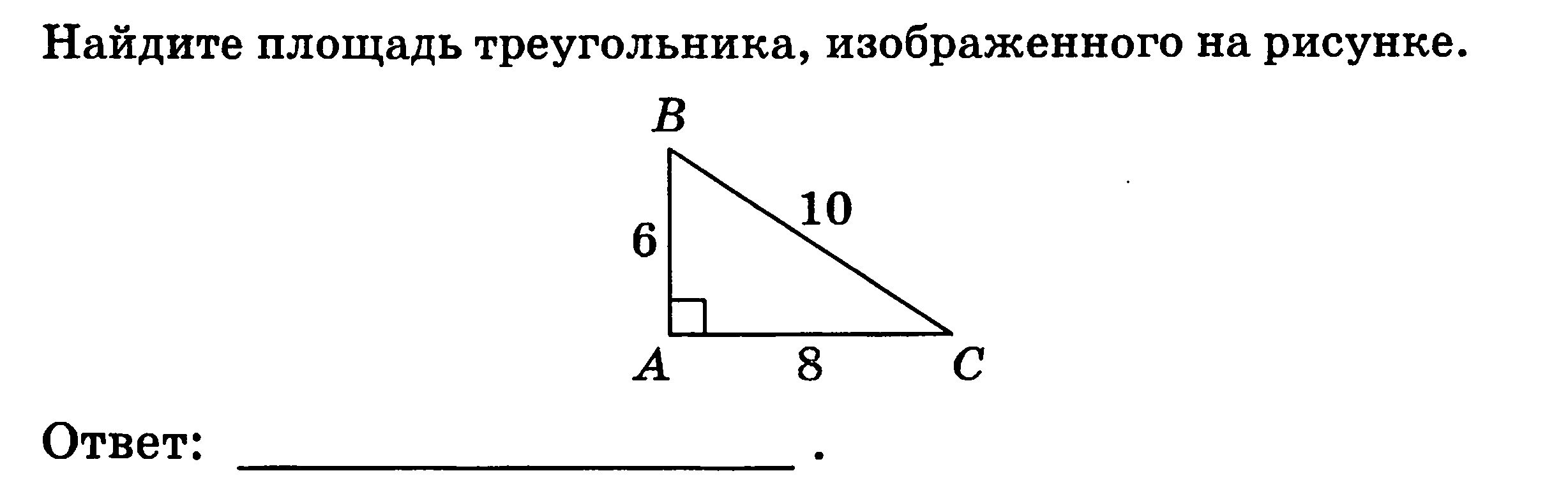 24 ( Ксения)
24 ( Ксения)
2. 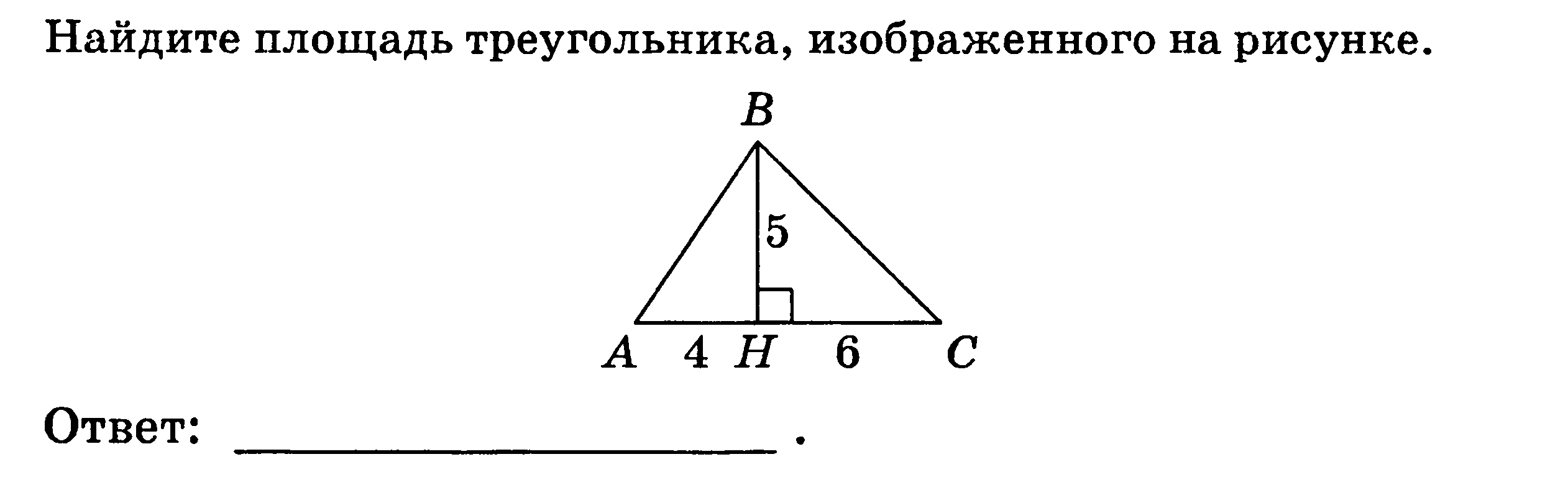 25 ( Максим)
25 ( Максим)
3. 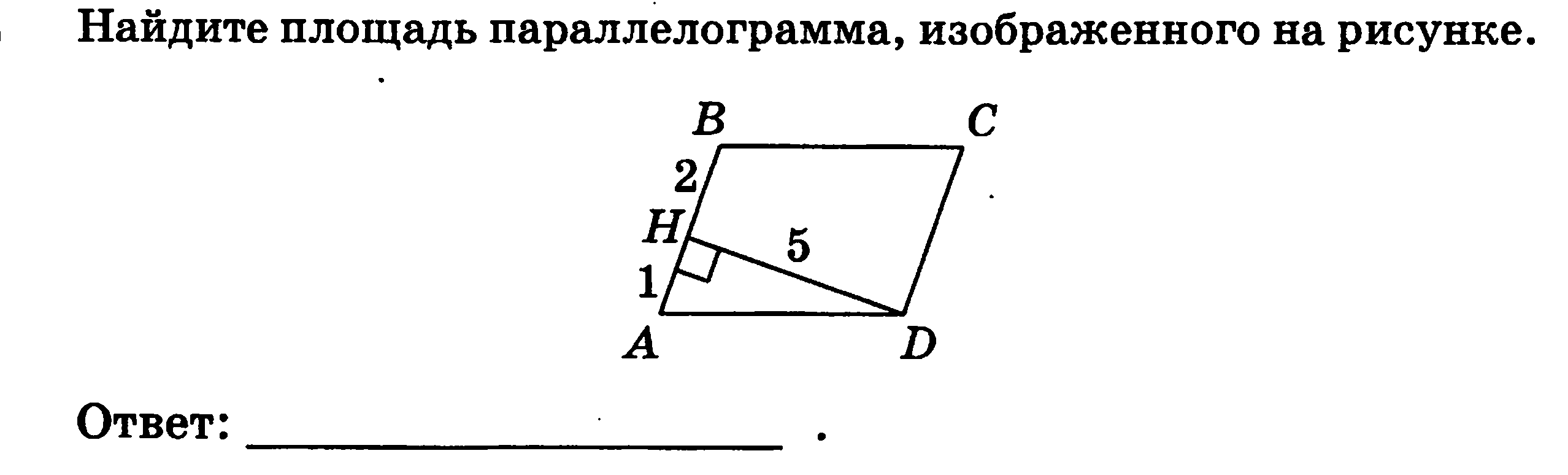 15 ( Игорь)
15 ( Игорь)
4. 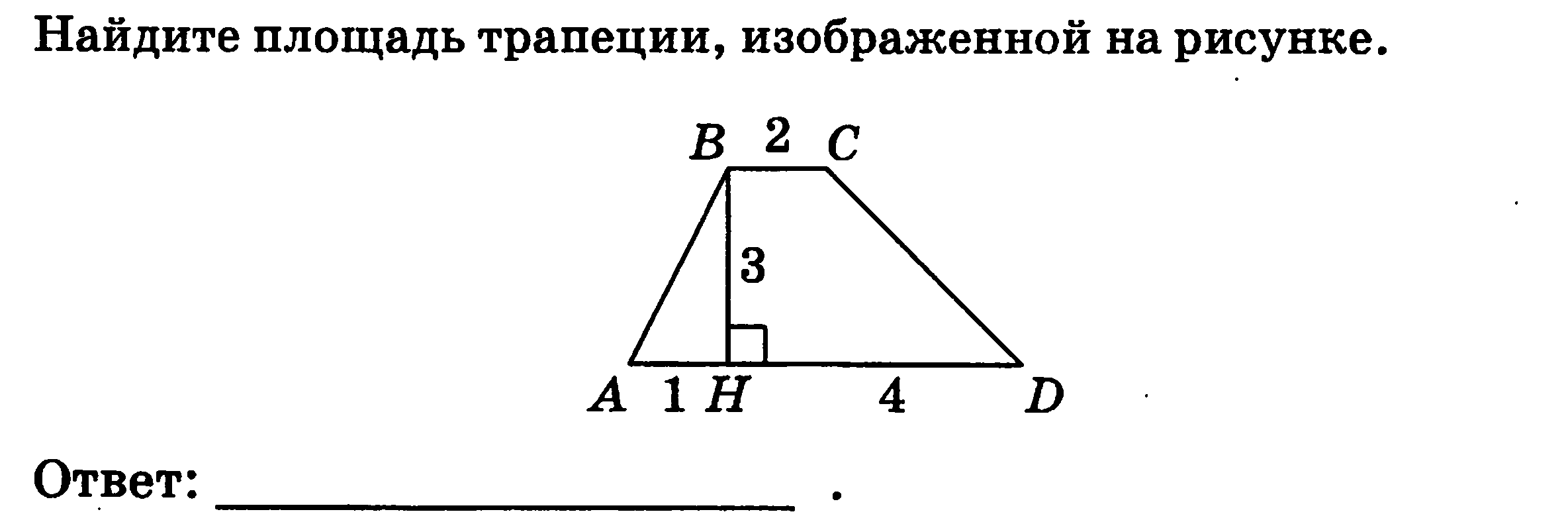 10,5 ( кто выполнил)
10,5 ( кто выполнил)
Вывод:
1. Определить вид многоугольника.
2. Вспомнить формулы, по которым вычисляются площади многоугольников.
3. Выделить для себя ту формулу, которая используется для нахождения площади данного вида многоугольника.
4. Найти площадь.
Выставление оценок в оценочный лист:
2 задания – «3»
3 задания – «4»
4 задания – «5»
IV. Физкультминутка
Упражнения для глаз (музыка)
V. Обобщение и систематизация знаний и умений учащихся.
Решение разноуровневых заданий.
(Учащиеся решают одну из задач самостоятельно) Приложение 3
Уровень А
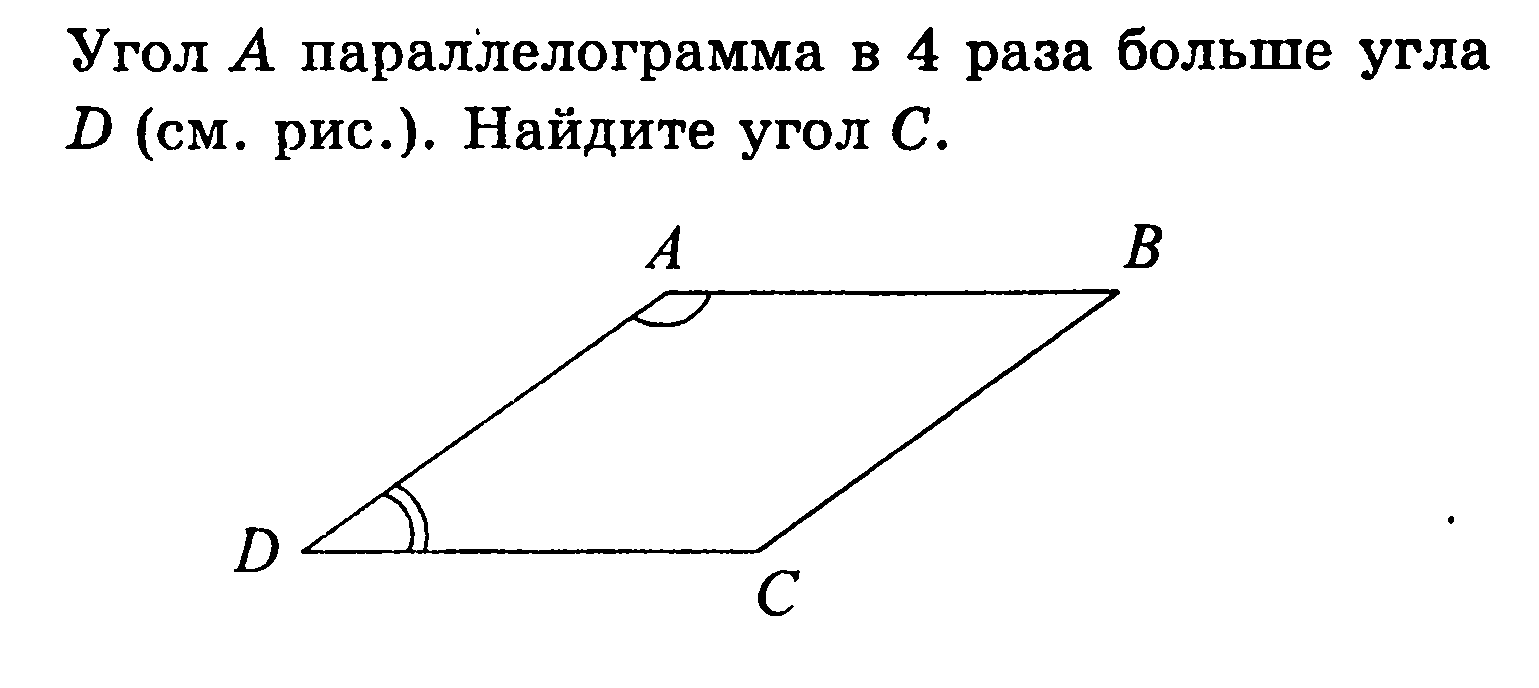 Ответ: 144°
Ответ: 144°
Уровень Б
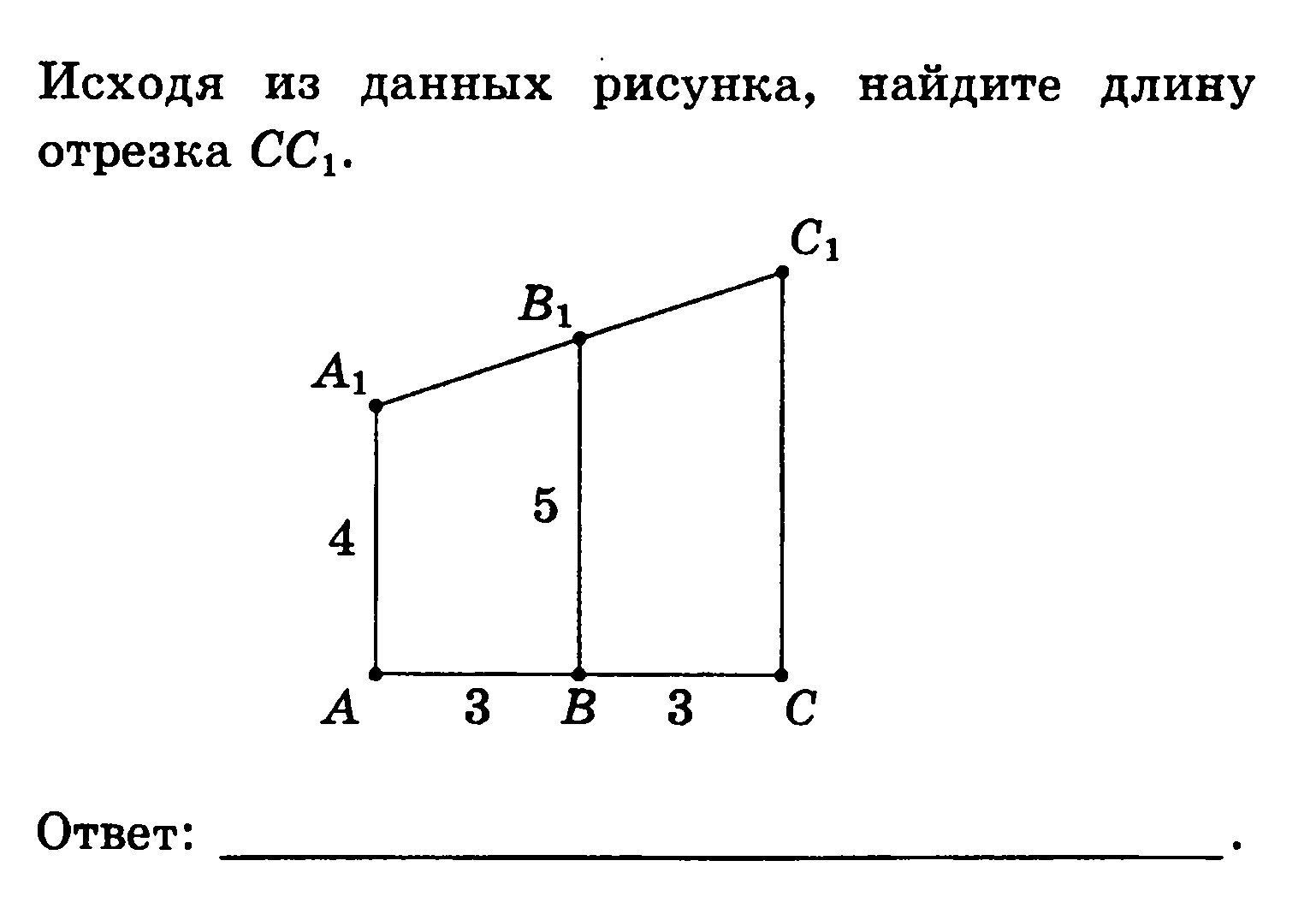 Ответ: 6
Ответ: 6
У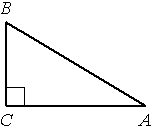 ровень В.
ровень В.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Ответ: 5
Оценки выставляют в оценочные листы.
А – «3»; В – «4»; С – «5».
2) Разбор решения задачи второй части модуля «Геометрия»
Учитель предлагает задание из второй части модуля геометрии.
Стоимость – 2балла. Условие: полное описание решения. (Слайд 7)

VI. Домашнее задание. (Слайд 8)
Выполнить задания № 15-20 и 24-26 Варианта 10 Сайт Гущина
VII. Индивидуальная работа.
Каждый ученик работает на индивидуальных опросных листах. К листу прикреплён бланк ответов, который по окончании заполняют и сдают учителю на проверку. А потом идёт самопроверка по слайду презентации.
Так как по требованию проведения экзамена необходимо, чтобы учащиеся из модуля « геометрия» выполнили не менее 2-х заданий, то удовлетворительная оценка может быть выставлена, если выполнено верно не менее 2-х заданий.
Вариант 15 (Ященко)
1 часть: Модуль «Геометрия».
Задание 15
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 73, сторона ВС равна 31, сторона АС равна 42. Найдите MN.
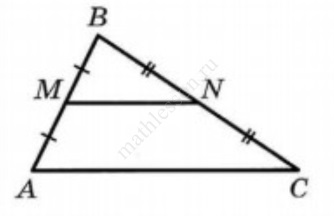
Ответ: 21
Задание 16
Угол А трапеции ABCD с основаниями AD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах.
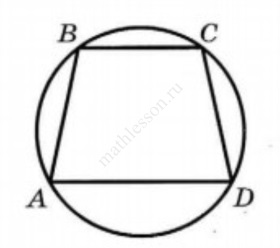
Ответ: 103
Задание 17
В ромбе ABCD угол АВС равен 68°. Найдите угол ACD. Ответ дайте в градусах.
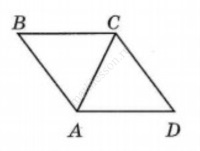
Ответ: 56
Задание 18
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник. Найдите его площадь.
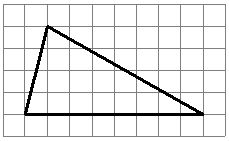
Ответ: 16
Задание 19
Какие из следующих утверждений верны?
Диагональ параллелограмма делит его на два равных треугольника.
Все углы ромба равны.
Площадь квадрата равна произведению двух его смежных сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: 13
2 часть: Модуль «Геометрия»
Задание 23. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если BK=10, СK=18.
Ответ: 76
Задание 24. Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что CD ⊥EF.
Задание 25. В треугольнике АВС биссектриса BE и медиана AD перпендикулярны и имеют
одинаковую длину, равную 96. Найдите стороны треугольника АВС.
Ответ: 24√13; 48√13; 72√5.
VIII. Этап подведения итогов занятия. Рефлексия. Оценить работу каждого учащегося. -Чем данный урок был полезен для Вас? -Какие пробелы в знаниях помог восполнить? -Что нового для себя Вы открыли на уроке?
(Листочки) Продолжите фразу:
У меня хорошо получается решать способом……………………………………………………………
Мне нужно ещё поработать над ………………….……………………………………………………….
На следующих уроках мне бы хотелось………….……………………………………………………….
……………………………………………………………………………………………………………….
Сдаём оценочные листы и листы рефлексии.
Спасибо за урок.
1 задание: Установить – истинное или ложное утверждение.
Вертикальные углы равны.
Сумма двух смежных углов равна 180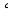 .
.
Сумма вертикальных углов равна 180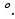
Если две стороны и угол одного треугольника соответсвенно равны двум сторонам и углу другого треугольника,то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответсвенно равны двум сторонам и углумежду ними другого треугольника,то такие треугольники равны.
В треугольнике против меньшего угла лежит меньшая сторона.
Длина окружности радиуса 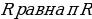 .
.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
Треугольник АВС, у которого АВ= 3,ВС=4, АС=5,является тупоугольным.
Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
Задание:
Вычислить площадь фигур
1)

2)

3)

4)

3 задание:
Решить задачи:
Уровень А

Уровень Б

У ровень В
ровень В
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
РЕФЛЕКСИЯ
Продолжите фразу:
У меня хорошо получается решать способом………………………………………………………………………………………..
Мне нужно ещё поработать над ………………….………………………………………………………………………………
На следующих уроках мне бы хотелось………….…………………………………………………………………………….
………………………………………………………………………………………………………………………………………………………………………………………………….
Оценочный лист
ФИ______________________________________________________
| Этап урока | Задание | Оценка ученика | Оценка учителя |
| I | Выбрать верные утверждения |
|
|
| Записать формулы |
|
|
| II | Вычислить площадь фигур по готовым чертежам |
|
|
| Выполнить разноуровневое задание |
|
|
| III | Индивидуальная работа |
|
|
|
| Средняя оценка за урок |
|
|
|
| Итоговая оценка за урок |
|
Вариант 15 (Ященко) ФИ _____________________________
1 часть: Модуль «Геометрия».
Задание 15
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 73, сторона ВС равна 31, сторона АС равна 42. Найдите MN.

Ответ: _____
Задание 16
Угол А трапеции ABCD с основаниями AD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах.

Ответ: _____
Задание 17
В ромбе ABCD угол АВС равен 68°. Найдите угол ACD. Ответ дайте в градусах.

Ответ: ___
Задание 18
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник. Найдите его площадь.

Ответ: ____
Задание 19
Какие из следующих утверждений верны?
Диагональ параллелограмма делит его на два равных треугольника.
Все углы ромба равны.
Площадь квадрата равна произведению двух его смежных сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ____
2 часть: Модуль «Геометрия»
Задание 23. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если BK=10, СK=18.
Задание 24. Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что CD ⊥EF.
Задание 25. В треугольнике АВС биссектриса BE и медиана AD перпендикулярны и имеют
одинаковую длину, равную 96. Найдите стороны треугольника АВС.






 Ребус (геометрия)
Ребус (геометрия) .
.
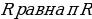 .
.








 24 ( Ксения)
24 ( Ксения) 25 ( Максим)
25 ( Максим) 15 ( Игорь)
15 ( Игорь) 10,5 ( кто выполнил)
10,5 ( кто выполнил) Ответ: 144°
Ответ: 144° Ответ: 6
Ответ: 6  ровень В.
ровень В. 














