Внеклассное мероприятие по математике на тему: «Теория Вероятностей и Статистики» для 9 класса

Муниципальное казенное образовательное учреждение

«Калукская средняя общеобразовательная школа»

Внеклассное мероприятие

по математике на тему:

«Теория Вероятностей и Статистики»

для 9 класса

Разработала: учитель математики

МКОУ «Калукская СОШ»

Макатова Медине Мустафаевна

Цель: Развивать интерес к изучению математики, повышать познавательную активность учащихся.

Задачи:

• Обучающая: Выработка навыков нешаблонного и логического мышления при решении нестандартных задач.

• Воспитательная: Воспитание коллективизма, уважения, чуткости и тактичности по отношению к окружающим, формирование способности к позитивному сотрудничеству.

• Развивающая: Развитие внимания, мышления, речи, памяти, умения анализировать, сравнивать, делать выводы.

Правила игры: из учащихся 9 классов заранее выбираются представители команд (по 5-6 человек в одной команде из 9 классов). Выбирают капитанов, которые будут отвечать на вопросы и задания. Жюри можно выбрать из старшеклассников. За каждый правильный ответ командам начисляется по 1 баллу. Зрителям тоже можно принять участие в игре (см. далее в описании). Все задания командам должны быть представлены не только через ММУ, но и в печатном виде. Вступительное слово учителя.

Вы, наверное, не раз слышали или сами говорили “это возможно”, “это не возможно”, это обязательно

случиться”, “это маловероятно”

Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти.

Случай, случайность – с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная ошибка. Этот ряд можно продолжать до бесконечности. Казалось бы, тут нет места для математики – какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности – они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями

Слово “событие” в быту применяют к значительным явлениям (день рождение, экзамен, свадьба), а в математике – ко всем возможным исходам рассматриваемой ситуации. Например, при бросании игральной кости событие- это выпадение той или иной грани.

Ход мероприятия.

1. Разминка

Какими буквами обозначаются события? Приведите примеры достоверных событий (смена дня и ночи); невозможных событий (2010 год наступит 1 июля 2009 года); возможных или случайных (в мае выпадет снег); равновозможных или равновероятных (подкидывание монеты).

Вопросы для команд (поднимают карточку с соответствующей буквой, за правильный ответ - 1 балл): какие из следующих событий – возможные (случайные), достоверные, невозможные

• Черепаха научится говорить

• Вода в чайнике, стоящем на горячей плите закипит

• День рождения вашего друга – 30 февраля

• Вы выиграете, участвуя в лотерее

• Вы не выиграете, участвуя в беспроигрышной лотерее

• На следующей неделе испортится погода

• Вы нажали звонок, а он не зазвонил

• После четверга будет пятница

• Летом у школьников будут каникулы

• По окончанию 9 класса учащиеся будут сдавать экзамен по алгебре

• Зимой выпадет снег

• При включении света, лампочка перегорит

• Вы выходите на улицу, а вам навстречу идёт слон

• Завтра пойдёт дождь

Ответы:

Событие	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Достоверное		+						+	+	+	+
возможное (Случайное)				+		+	+					+		+
Невозможное	+		+		+								+

Зрителям тоже можно предложить заполнить такие таблицы.

1. Придумки

Задача команд: придумать по одному достоверному, возможному, невозможному событию. Предложить их команде-противнику, чтобы они определили вид события.

1. Вычислялки

Впервые вероятность случайных событий в играх вычислили в XVII веке французские математики Блез Паскаль и Пьер Ферма. Они подсчитали число шансов события из общего возможного числа равновероятных исходов. Они вывели классическое определение вероятности (повторить перед решением задач).

Классическое определение вероятности: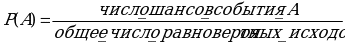

m – число шансов события А, n – общее число равновероятных исходов.

Команде 1:

1.Хорошо перетасуем колоду из 36 карт, случайно вынем 1 карту. Какова вероятность того, что вытянут туз?

2.В лотерее 100 билетов, из них 5 выигрышных. Какова вероятность проигрыша?

3. В ящике лежат 8 красных,2 синих, 20 зеленых карандашей. Вы наугад вынимаете карандаш. Какова вероятность того, что это красный карандаш? Чёрный карандаш?

Решение задач команды 1.

1.

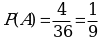
2.

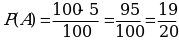
3.А={вынут красный карандаш},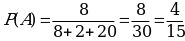

В={вынут чёрный карандаш},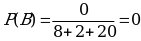

Команде 2:

1.На экзамене -24 билета. Андрей не разобрался в одном билете и очень боится его вытянуть. Какова вероятность, что Андрею достанется несчастный билет?

2.В лотерее 10 выигрышных билетов и 240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?

3. В ящике лежат 8 красных,2 синих, 20 зеленых карандашей. Вы наугад вынимаете карандаш. Какова вероятность того, что это зелёный карандаш? Не желтый карандаш?

Решение задач команды 2.

1.

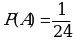
2.

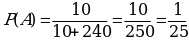
3. А={вынут зелёный карандаш},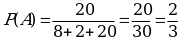

В={вынут не жёлтый карандаш},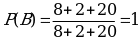

Пока команды работают, то зрителям можно предложить составить слова из букв слова ВЕРОЯТНОСТЬ или КОМБИНАТОРИКА и записать их на отдельные листы.

1. Статистика

Статистика - наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово “статистика” происходит от латинского слова status, которое означает “состояние, положение вещей”. Результаты статистических исследований широко используют для практических и научных выводов.

У трех друзей Петра, Артёма– к концу четверти по алгебре оказались следующие отметки:

Петр: 5;4;4;3;5;4;5;5;4;3;5;5;

Артём: 3;3;2;3;4;4;4;3;3;2;4;4.

Запишите упорядоченный ряд данных для каждого ученика и ответьте на вопросы:

а) Какой средний балл имеет к концу четверти каждый ученик?

б) Какова наиболее типичная, характерная отметка каждого из них?

в) Какова средняя отметка каждого ряда?

г) Чему равна разность между наибольшей и наименьшей отметками?

д) Сколько раз в четверти был опрошен ученик?

Какую отметку вероятнее всего получит каждый из друзей за четверть?

1. Подведение итогов

Жюри подсчитывает баллы, заработанные командами. Если их количество равное, то можно дополнительно предложить ответить на дополнительные вопросы (по очереди). Если одна команда не отвечает, то есть шанс у другой команды заработать очки.

Вопросы:

- Какой статистической характеристикой можно назвать средний балл (среднее арифметическое)?

- Какой статистической характеристикой можно назвать наиболее типичную отметку (частота)?

- Какой статистической характеристикой можно назвать среднюю отметку каждого ряда (медиана)?

- Какой статистической характеристикой можно назвать разность между наибольшей и наименьшей отметкой (размах)?

- Какой статистической характеристикой можно назвать число, которое показывает, сколько раз был спрошен ученик (объём)?

Командам вручить дипломы и призы, наиболее активных зрителей можно отметить оценками в журнал.