Задание 10
Задание 10 № 520199 
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 5 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 8 апреля в Волшебной стране будет отличная погода.
Спрятать решение
Решение.
Для погоды на 6, 7 и 8 апреля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды:
P(XXO) = 0,9·0,9·0,1 = 0,081;
P(XOO) = 0,9·0,1·0,9 = 0,081;
P(OXO) = 0,1·0,1·0,1 = 0,001;
P(OOO) = 0,1·0,9·0,9 = 0,081.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,081 + 0,081 + 0,001 + 0,081 = 0,244.
Ответ: 0,244.
Задание 10
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение.
6 июля погода может быть отличной при следующих исходах:
| 4 июля | 5 июля | 6 июля |
| Погода | Вероятность | Погода | Вероятность | Погода | Вероятность |
| Хорошая | 0,8 | Хорошая | 0,8 | Отличная | 0,2 |
| Хорошая | 0,8 | Отличная | 0,2 | Отличная | 0,8 |
| Отличная | 0,2 | Хорошая | 0,2 | Отличная | 0,2 |
| Отличная | 0,2 | Отличная | 0,8 | Отличная | 0,8 |
Вероятности в таблице проставлены из следующих соображений. Текущая погода 3 июля хорошая, тогда, с вероятностью 0,8 она будет такой же в следующий день (то есть 4 июля), а с вероятностью 1-0,8=0,2 изменится на отличную. Аналогично для всех последующих дней. Так как события изменения погоды независимы друг от друга, то получаем вероятности исходов для каждой строки таблицы:
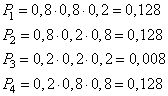
Таким образом, погода 6 июля будет отличной или при первом исходе, или при втором, или при третьем, или при четвертом:
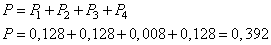
(Здесь учтено, что исходы несовместны между собой, то есть не могут произойти одновременно).
Ответ: 0,392.