"Золотое сечение и реклама"

11

Министерство образования и науки Российской Федерации

МКОУ Верхнехавская СОШ №1

Исследовательская работа

ЗОЛОТОЕ СЕЧЕНИЕ И РЕКЛАМА

Выполнил: Чулков Егор,

ученик МКОУ Верхнехавская СОШ №1 6 А класса

Руководитель: Буковшина О.Н., учитель математики

с.Верхняяя Хава

2016

Содержание

1.Введение ---------------------------------------------------------------------3 стр

2. История золотого сечения -----------------------------------------------4 стр

3. Математическая сущность золотого сечения -----------------------7 стр

4. Золотое сечение в окружающей действительности ---------------10 стр

5. Золотое сечение и реклама ---------------------------------------------- 12 стр

5. Заключение -----------------------------------------------------------------17 стр

Список литературы------------------------------------------------------------19 стр

Приложение

Введение

Посещая различные торговые центры, проходя по улицам, я обращаю внимание на рекламные вывески и витрины. Меня заинтересовал тот факт, что мимо одних проходишь, и ничего не запоминается, а некоторые рекламные банеры и оформленные витрины практически завораживают своим дизайном. На уроке математики мы узнали знаменитый пифагорейский лозунг «Числа правят миром». И тогда я задумался, а вдруг в этом и есть разгадка. Мне захотелось узнать, нет ли в математике какого-либо правила, закона, благодаря которому различные изображения становятся притягательными для нашего зрения. При изучении темы «Пропорции» я узнал, что есть особенная пропорция, называемая «золотым сечением», но в школе на уроках мы этот материал не изучаем. Как оказалось, «классическая» наука и педагогика его игнорируют, а «официальная» математика не признаёт. Хотя четыре столетия назад немецкий астроном и математик Иоганн Кеплер сравнил это соотношение «с драгоценным камнем».

Цель данной работы провести краткий обзор истории и математической сущности золотого сечения, и попытаться осмыслить его роль в окружающей действительности и в дизайне рекламной продукции..

1. История золотого сечения

В математике принцип «золотого сечения» впервые был сформулирован в «Началах» Евклида, самом известном математическом сочинении античной науки, написанном в III веке до н.э. Переводчик Дж. Kампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

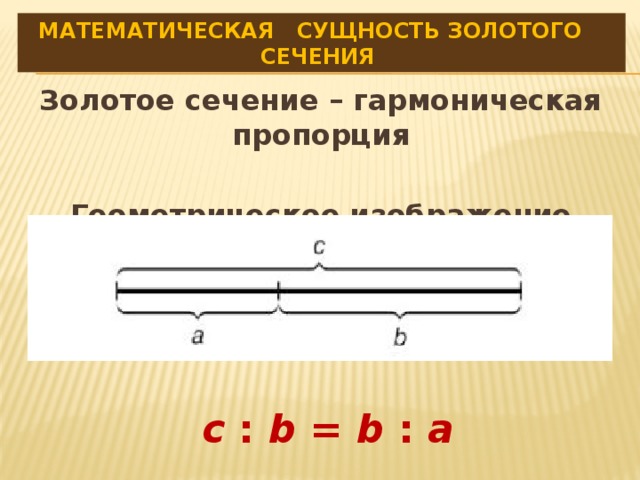
Если упростить задачу Эвклида, то отрезок линии АВ будет считаться разделенным точкой С (которая ближе к точке А) в «золотой пропорции», если отношение большей части СВ к меньшей АВ равно отношению всего отрезка АВ к большей части СВ, т.е. СВ: АС=АВ: СВ. Результатом решения этой задачи является иррациональное число, приблизительно равняющееся 1,618, которое и называют золотым сечением, золотым числом или золотой пропорцией. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.

В целом все первые геометрические системы – эвклидова геометрия, теорема Пифагора – свидетельствуют о том, насколько волновали древних греков проблемы гармонии, поиск идеальных пропорций и форм. Однако есть предположение, что первыми к принципу золотого сечения пришли все же египтяне. Наиболее известная пирамида Хеопса построена с использованием золотого треугольника, в котором соотношение гипотенузы к меньшему катету равно золотому сечению. Храмы, барельефы, предметы быта и украшения из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения. Эстетическим каноном древнегреческой культуры этот принцип стал благодаря Пифагору, который изучал в стране пирамид тайные науки египетских жрецов. Их результат воплощен в фасаде древнегреческого храма Парфенона, где присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. Также с использованием золотого сечения созданы Афродита Праксителя и театр Диониса в Афинах. Последовательно отсекая от «золотых прямоугольников» квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, можно получить довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали. Платон (427-347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

Во времена средневекового Ренессанса гениальный итальянский математик Лука Пачоли написал первую книгу о золотом сечении, назвав ее «Божественной пропорцией». По его мнению, даже Бог использовал принцип золотого сечения для создания Вселенной. Эта идея была позже использована Кеплером, последняя книга которого так и называлась – «Гармония Вселенной». В то же самое время Леонардо да Винчи, другом которого был Пачоли, использовал для композиционного построения своей знаменитой Джоконды «золотой равнобедренный треугольник», в котором отношение бедра к основе равно золотому сечению. Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название «золотое сечение». В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил «золотому сечению».

2. Математическая сущность золотого сечения

Отрезок прямой АВ можно разделить точкой C на две части следующими способами:

· на две равные части АВ: АC = АВ: ВC;

· на две неравные части в таком отношении, когда АВ: АC = АC: ВC.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение можно построить. (Приложение 1)

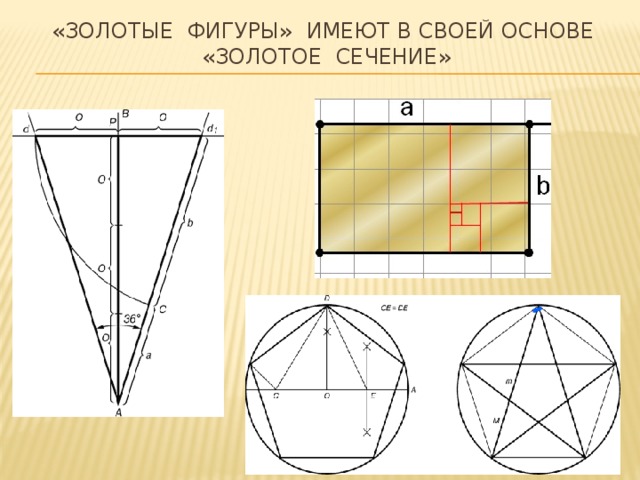
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении. Широкое распространение получили «золотые фигуры», имеющие в своей основе «золотое сечение».

Золотой прямоугольник

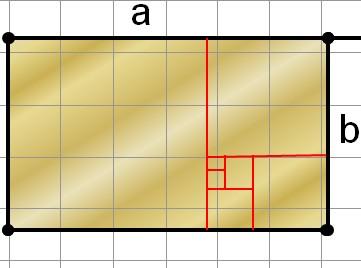
Прямоугольник с «золотым» отношением сторон стали называть «золотым прямоугольником». Он также обладает интересными свойствами. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности. А если провести диагональ первого и второго прямоугольника, то точка их пересечения будет принадлежать всем получаемым золотым прямоугольникам

«Золотой треугольник» – это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1.618.

В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются «золотыми треугольниками». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться. Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

3. Золотое сечение в окружающей действительности

В поисках ответа на свой вопрос я узнал, что «золотая пропорция» буквально пронизывает всю нашу действительность. Судите сами. Одним из первых проявлений золотого сечения в природе подметил разносторонний наблюдатель, автор многих смелых гипотез немецкий математик и астроном Иоганн Кеплер (1571 – 1630). С XVII в. наблюдения математических закономерностей в ботанике и зоологии стали быстро накапливаться. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция. Интерес человека к природе привёл к открытию её физических и математических закономерностей. Красота природных форм рождается во взаимодействии двух физических сил – тяготении и инерции. Золотая пропорция – это математический символ этого взаимодействия, поскольку выражает основные моменты живого роста: стремительный взлёт юных побегов сменяется замедленным ростом «по инерции» до момента цветения. Рассматривая расположение листьев на общем стебле многих растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте «золотого сечения».

Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом.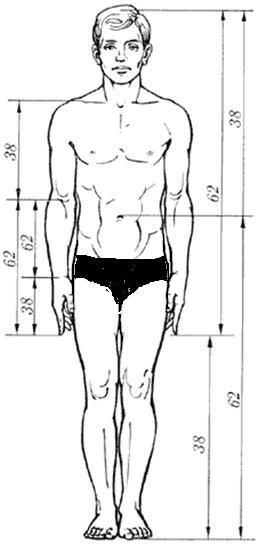

В настоящее время «спираль Архимеда» широко используется в технике. В гидротехнике по «золотой спирали» изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.

«Золотую спираль» также можно заметить в созданиях природы. Например, расположение семечек в корзине подсолнечника. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнечника закручено 13 спиралей, в другую – 21. Отношение 13: 21 – «золотая пропорция». Похожее спиральное расположение наблюдается у чешуек сосновых шишек или ячеек ананаса. По золотой спирали свёрнуты раковины многих моллюсков, некоторые пауки, сплетая паутину, закручивают нити вокруг центра по золотым спиралям. Рога архаров закручиваются по золотым спиралям. Природа повторяет свои находки, как в малом, так и в большом. По золотым спиралям закручиваются многие галактики, в частности и галактика Солнечной системы.

4. Золотое сечение и реклама

Еще в эпоху Возрождения художники открыли, что существуют правила, которым подчиняется человеческое восприятие. К примеру, независимо от размера и формата холста картины имеют определенные точки, приковывающие взгляд, — это так называемые зрительные центры. Психофизическое восприятие человека таково, что изображение, размещенное с учетом данных точек, выглядит законченным, гармоничным. 

Таких точек всего четыре, и находятся они на расстоянии 3/8 и 5/8 от соответствующих краев холста
Если нужно обратить внимание зрителя на тот или иной элемент изображения, достаточно совместить его с одним из зрительных центров. Современные фотокамеры, например цифровая зеркальная камера Canon EOS 20D, упрощают задачу построения правильной композиции, автоматически фокусируя кадр в соответствии с правилом золотого сечения. 
Правило золотого сечения, или правило Леонардо, наверняка известно всем без исключения современным дизайнерам, фотографам, иллюстраторам. 

Графическая иллюстрация правила золотого сечения.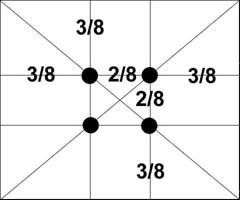 

Более того, чаще всего они даже не задумываются о том, что применяют в своей работе правила классической композиции.
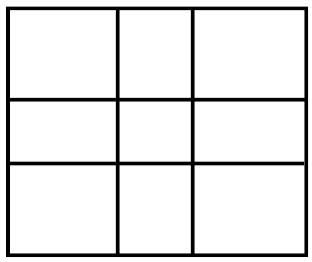
Некоторые рекламисты ошибочно полагают, что в рекламе правила классической композиции неприменимы, что реклама — индустрия современная и дерзкая, где не место шаблонам, стандартам и правилам, что реклама — это бизнес: ее задача — не радовать глаз, а продавать. Однако, если мы посмотрим на образцы самой удачной с коммерческой точки зрения, самой «продающей» рекламы, то увидим то же золотое сечение, то же равновесие, тот же ритм, тот же контраст… Правила классической композиции — это признак грамотности и хорошего вкуса в рекламе. В мировой практике предостаточно примеров как удачной, так и ничем не примечательной, заурядной, бесполезной рекламы. Тот, кто ценит собственное время и силы, наверняка предпочтет учиться на ошибках, а лучше – на успехах других. Правило золотого сечения со временем было упрощено в крайне популярное сегодня правило «одной трети». Согласно этому правилу формат картины, фотоснимка или любого другого изображения условно делится на девять равных частей, при чем точки пересечения – и есть четыре зрительных центра. Любуясь произведениями художников-классиков, задумывались ли вы о золотом сечении? Присмотревшись повнимательнее, вы увидите, что оно соблюдается в полотнах Репина, Левитана, Шишкина, Айвазовского и многих других мастеров
Соблюдение правила «одной трети» в полотнах выдающихся художников. 

Соблюдение правила «одной трети» в работах современных фотографов
Опытные рекламисты знают, как уловить мимолетный взгляд и использовать его по максимуму. Рассмотрим пример — образец рекламы бренда Marlboro

 
Успешность рекламных изображений этой торговой марки по большому счету обусловлена талантливо выполненными фотоснимками. Вспомним о золотом сечении. Соблюдено ли оно? Стадо лошадей на бескрайних просторах, символизирующее свободу, игра света и тени на траве, слоган и изображение пачки — все расположено в соответствии с золотым сечением, все вызывает ощущение спокойствия, гармонии, красоты. 
Расположение элементов рекламного изображения в соответствии с правилом золотого сечения позволяет рекламистам сделать акцент на первостепенные детали, вывести на передний план то, что должно доминировать. К тому же гармонично построенное изображение наверняка вызовет положительные эмоции у потребителя, чего и добивается рекламист. Присутствие в изображении четко выраженных горизонталей и вертикалей, делящих формат на равные части по правилу «третей», создают ощущение уравновешенности, покоя, стабильности.

Весьма часто встречаются узкие и очень длинные плакаты-транспаранты (например, перетяжки, с помощью которых оформляются улицы; транспаранты, устанавливаемые вдоль дорог, на фасадах зданий, в помещениях), в которых текст располагается в строку. Благоприятное для глаза соотношение высоты букв и ширины такого транспаранта также может быть обеспечено пропорцией золотое сечение. Если текст компонуется в две и более строки одинаковыми по высоте прописными буквами, то междустрочное расстояние тоже может соотноситься с высотой букв, как 0,618:1. Если глаз не воспринимает изображение как единое целое (безразлично, идет ли речь об отдельном плакате или перетяжке, или о комплексе), если он блуждает по разным элементам или его отвлекают частности, то это означает, что в композиции нет зрительного центра, особого акцента, который бы связал все в единое целое.
Вывеска сложной формы построена по принципу "золотого сечения". Размер консолей и расстояние между ними 350 х 350 мм. Формула, придуманная самим великим Микеланджело, нашла применение и в наружной рекламе. Вывеска, которая до последнего момента вызывала сомнения: как получится? будут ли читаться символы на консолях? - превзошла все ожидания. 

Многие рекламщики рекомендуют соблюдать пропорции золотого сечения, размещая образцы на витринах. Отношение целого отрезка к большей части должно равняться отношению большей части к меньшей. Если целое взять за 100 процентов, то больший отрезок составит 62 процента, меньший 38. Считается, что подобное расположение – самое гармоничное. 
Пример  
Глубина витрины – 65 см. Значит, товар должен находиться примерно в 40 см (65 см x 62%) от той части, что выходит на улицу. В 25 см (65 см x 38%) – от обращенной к магазину. Если мы, взяв три вещи, выложим их в цепочку, то опять-таки стоит посмотреть на пропорцию. При длине отрезка в метр первый товар находится в 62 см от второго. Второй от третьего – в 38. 

5. Заключение

Современные программы образования в таких странах, как США, Канада, Россия показывают, что в большинстве из них нет даже упоминания о «золотом сечении». То есть, имеет место сознательное игнорирование одного из важнейших открытий античной математики. Возможно, причину следует искать в негативном отношении современной «материалистической» науки и «материалистического» образования к астрологии и так называемым «эзотерическим» наукам. В них «золотое сечение» и связанные с ним геометрические фигуры – «пентаграмма», «Платоновы тела» – широко используются в качестве основных «сакральных» символов. И «материалистическое» образование не нашло ничего более разумного, как выбросить золотое сечение на свалку «сомнительных научных концепций» вместе с астрологией и «эзотерическими» науками. В результате большинство «образованных» людей хорошо знают «теорему Пифагора», но имеют весьма смутное представление о «золотом сечении». Несмотря на неприятие «золотого сечения» современными «официальными науками», оно повсеместно используется в технике, во многих странах мира, в том числе в России. Крупные учёные продолжают изучать и искать практическое применение одному из «золотых» математических принципов. В настоящее время исследуются математические теории связанные с принципами «золотого сечения». Математика гармонии применима и к современной экономике. Довольно известны, например, работы российского ученого Харитонова об экономическом развитии российских регионов и страны, в целом исходя из принципов золотого сечения. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. «Математика гармонии» существенно дополнит классическую математику.

В заключении сформулирую наиболее популярное и понятное определение «золотого сечения».

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Нами был проведен исторический экскурс и разобрана математическая сущность «золотого сечения», рассмотрено строение «золотых фигур».

Знакомство с принципами «золотого сечения» помогло мне получить ответ на мой вопрос, а также увидеть гармонию и целесообразность окружающих нас творений природы и человека.

Можно сделать выводы:

• золотое сечение – это один из основных основополагающих принципов природы;

• человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе;

• дизайн успешной «продающей» рекламы тесно связан с понятием золотого сечения;

• «Математика гармонии» повлечет в теории новые и наверняка очень интересные математические результаты.

Список литературы

1. Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс. – М.: Школа-пресс, 1998.

2. Васюткинский Н.Н. Золотая пропорция. – М., 1990.

3. Волошинов А.В. Математика и искусство. – М., 1992.

4. Гарднер М. Математические головоломки и развлечения. – М., 1994.

5. Кованцов Н.И. Математика и романтика. – Киев, 1976.

6. МСЭ // под редакцией Б.А. Введенского. – М. 1959.

7. Пидоу Д. Геометрия и искусство. – М.: Мир, 1989.

8. Прохоров А.И. Золотая спираль // Квант. 1984. № 9.

Золотое сечение и реклама

Выполнил: Чулков Егор, обучающийся 6А класса

МКОУ Верхнехавская СОШ №1

Руководитель: Буковшина О.Н., учитель математики

История золотого сечения

Немецкий астроном и математик Иоганн Кеплер сравнил это соотношение «с драгоценным камнем».

Впервые сформулирован принцип «золотого сечения»

Театр Диониса

Парфенон

Древнегреческий ученый Архимед первым обратил внимание на изящную кривую

Портретный деревянный рельеф «Зодчий Хесира» создан в начале III тысячелетия до н.э.

Основатели учения о золотом сечении

ПИФАГОР ВВЁЛ ПОНЯТИЕ О ЗОЛОТОМ ДЕЛЕНИИ

Леонардо да Винчи ввёл термин «золотое сечение»

Математическая сущность золотого сечения

Золотое сечение – гармоническая пропорция

Геометрическое изображение

с : b = b : а

Построение золотого сечения

«Золотые фигуры» имеют в своей основе «золотое сечение»

Золотое сечение и окружающая действительность

Золотое сечение и окружающая действительность

Золотое сечение и окружающая действительность

Золотое сечение и окружающая действительность

Золотое сечение и окружающая действительность

Золотое сечение и реклама

Работа с рекламными плакатами

Если на клетке слона написано «буйвол» – не верь глазам своим!

СПАСИБО