Çyzykly funksiýa

Ç yzykly funksiýa we onuň grafigi.

6 synp.

Jumaýew Abdylalym Amanmyradowiç

Öý işini soramak:

• Funksiýa y=2 x+5 formula bilen berlipdir.Tablisany dolduryň:

x

y

-4

-3

-2

-1

0

1

2

3

4

x

y

-4

-3

-3

-2

-1

-1

1

3

0

5

1

2

7

3

9

11

4

13

Jumaýew Abdylalym Amanmyradowiç

• Funksiýa y=2 x+5 formula bilen berlipdir.Tablisany dolduryň:

x

y

-4

-3

-2

-1

0

1

2

3

4

x

y

-4

-3

-3

-2

-1

-1

1

3

0

5

1

2

7

3

9

11

4

13

Jumaýew Abdylalym Amanmyradowiç

• Funksiýanyň grafigi berlipdir. Tablisany dolduryň:

x

x

y

-3

y

-3

0

0

6

1

1

5

2

2

5

3

3

4

4

4

2

5

5

0

-2

Geçilen temany jemlemek:

Jumaýew Abdylalym Amanmyradowiç

A wtomobil 70 km/sag hemişelik tizlik bilen hereket edýär.Geçilen ýoly tapmagy aňladýan funksiýany tapyň.

S = 70 · t

Eger t = 1 bolsa, onda

S = 70 · 1 = 70

E ger t = 1,5 bolsa, onda

S = 70 · 1,5 = 105

E ger t = 3 bolsa, onda

S = 70 · 3 = 210

S = 70 · t

Bagly üýtgeýän ululyk

FUNKSIÝA

Bagly däl üýtgeýän ululyk

ARGUMENT

Howanyň temperaturasy bilen wagtyň arasyndaky baglanyşyk

Т 0 ,С

4

2

t , s

0

14

10

8

12

20

18

6

4

16

22

2

24

-2

о

Т= -6 С

t = 4s

-4

о

Т= 2 С

t = 12s

о

-6

Т= 4 С

t = 14s

t - argument

T - funksiýa

о

Т= -4 С

t = 24s

7

K wadratyň meýdanynyň onuň tarapyna baglylyk funksiýasyny tapyň

S = a 2

a = 2

S = 4

a = 3

a = 4

S = 9

S = 16

FUNKSIÝA

ARGUMENT

Funksiýanyň grafigi.

F unksiýanyň grafigi – bu abssissalary argumentiň

bahasyna, ordinatalary funksiýanyň degişli bahalaryna

deň bolan kooordinata tekizliginiň ähli nokatlarynyň

köplügini.

Ýatla!

II

I

IV

III

Funksiýanyň grafigi.

F unksiýanyň grafigi – bu abssissalary argumentiň

bahasyna, ordinatalary funksiýanyň degişli bahalaryna

deň bolan kooordinata tekizliginiň ähli nokatlarynyň

köplügi.

Ýatla!

A (-4; 6)

D (0; -5)

B (5; -3)

C (2; 0)

H aýsy çyzgyda funksiýanyň grafigi görkezilen?

A rgumentiň her bir bahasyna funksiýanyň ýeke-täk bahasy degişli

у

у

Используется триггер. На овал «2» - надо нажать два раза. Переход на следующий слаыд – щелчком мышки по пустому полю слайда.

berekella!

pikirlen!

0

х

0

х

1.

2.

Täze temany düşündirmek:

Jumaýew Abdylalym Amanmyradowiç

y = kx +b görnüşli funksiýa çyzykly funksiýa diýilýär, bu ýerde k we b sanlar, x we y üýtgeýän ululyklar.

x – argument

y – funksiýa

Jumaýew Abdylalym Amanmyradowiç

у = 2 х + 3

= 0 +3 = 3

у = 2 · +3

х

х =

0

(0 ; 3)

= 4+3 =7

у = 2 · +3

х =

2

х

(2 ;7)

M aslahat:

k koeffisient položitel san bolsa, onda argumentiň položitel bahalaryny saýla; eger otrisatel san bolsa, onda argumentiň otrisatel bahasyny saýla.

15

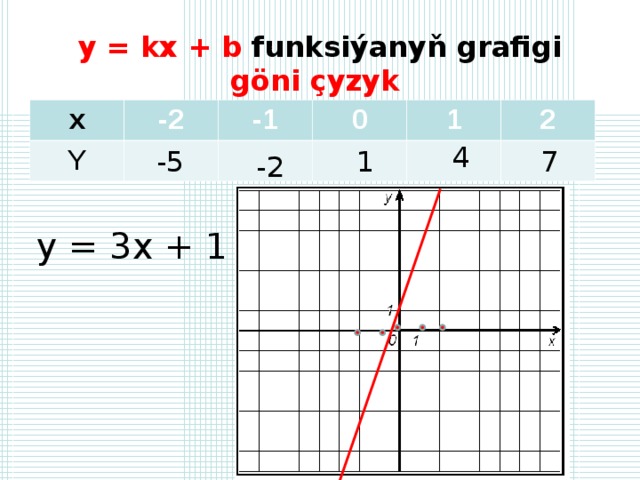
y = kx + b funksiýanyň grafigi göni çyzyk

x

-2

Y

-1

0

1

2

4

1

-5

7

-2

y = 3x + 1

I slendik iki nokadyň üsyünden bir we diňe bir göni çyzyk geçirip bolar.

Ç yzykly funksiýanyň grafigini gurmak üçin diňe iki nokat ýeterlikdir!

у = -2х +1

0

-2

х

у

5

1

у = 2х - 5

0

3

х

у

-5

1

k

koeffisiente

burç koeffisienti diýilýär.

y = 0,5 х +2

k = 1

0

4

х

у

k = 4

2

4

k = 0,5

y = 4 х +2

1

0

х

у

6

2

y = х +2

3

0

х

у

2

5

k burç koeffisientiniň ulalmagy bilen funksiýanyň Ox ok bilen emele getirýän burçy hem ulalýar .

0 bolsa, onda funksi ý any ň Ох ok bilen emele getriýän burçy ýiti burç . y х E ger sag el çep elden ýokarda bolsa, onda k0 " width="640"

k 0 bolsa, onda funksi ý any ň Ох ok bilen emele getriýän burçy ýiti burç .

y

х

E ger sag el çep elden ýokarda bolsa, onda

k0

k bolsa, onda emele gelen burç kütek burç.

y

x

E ger sag el çep elden aşakda bolsa, onda

k

k = 0 - funksiýanyň grafigi Ох oka parallel

y

x

k = 0

B urç koeffisientleri deň bolan birnäçe funksiýalaryň grafiklerini guralyň.

26

у = -х + 4

-2

0

х

у

4

6

у = -х

-3

0

х

у

3

0

у = -х - 5

-6

0

х

у

-5

1

Eger funksiýalaryň bu rç koeffisientleri deň bolsalar, onda olar paralleldirler.

Jumaýew Abdylalym Amanmyradowiç

у = -3х + 4

0

-1

х

у

4

7

4

у = х + 4

0

2

х

у

4

6

у = 2х + 4

0

1

х

у

6

4

29

Ç yzykly funksiýanyň grafigi Oy oky (0;b) nokatda kesýär.

х = 0 , y = k · x + b = k · 0 + b = 0 + b = b .

Jumaýew Abdylalym Amanmyradowiç

29

Täze temany berkitmek:

Jumaýew Abdylalym Amanmyradowiç

29

634-nji gönükme

y=4 x formula bilen berlen funksiýanyň grafigini guruň.

Grafik boýunça:

• argumentiň; 0,5; 1; 1,5; 2 ; 2,5; 3 bahalryna funksiýanyň haýsy bahalarynyň degişlidigini;
• funksiýanyň 4-; 0; 4 bahalaryna argumentiň haýsy bahalarynyň degişlidigini;
• argumentiň haýsy bahalarynda funksiýanyň položitel bahalara we argumentiňň haýsy bahalaryna fukssiýanyň otrisatel bahalara eýe bolýandygyny görkeziň.

Jumaýew Abdylalym Amanmyradowiç

29

29

29

29

Otrisatel baha eýe

Položitel baha eýe

29

Öý işi:

636-njy gönükme

Jumaýew Abdylalym Amanmyradowiç

29