Деревья. Цикломатическое число. Остов

Дискретная математика

Деревья. Цикломатическое число. Остов

План:

• Циклические и ацеклические ребра
• Понятие дерева и его элементов
• Представление деревьев
• Лес, остов, бинарное дерево

Циклические и ацеклические ребра

А

Ребро произвольного графа называется циклическим , если оно принадлежит хотя бы одному элементарному циклу в графе.

В противном случае – ацеклическим .

F

B

H

I

E

C

D

K

FE, FH, HK, KE - циклические

Цикломатическое число -

это число равное (G)=m(G)+c(G)-n(G)

где

m(G) - число ребер графа

c(G) - число связных компонент графа

n(G) - число вершин графа

Если неориентированный граф связный, то c(G)=1.

Если граф не связный, то разбить его на связные компоненты и посчитать их.

Понятие дерева и его элементов

Деревом называется конечный связный граф, с выделенной вершиной (корневой) и не имеющий циклов.

Дерево – это граф, предназначенный для отображения таких связей между объектами как вложенность, подчинённость, наследование.

Вершины в дереве называют узлами.

Расстояние до корневой вершины называют ярусом.

Теорема : Дерево с n – вершинами содержит (n-1) - ребро

Цикломатическое число любого дерева равно 0. Цикломатическое число леса равно сумме цикломатических чисел деревьев, то есть равно 0.

Для всех остальных графов цикломатическое число всегда положительное.

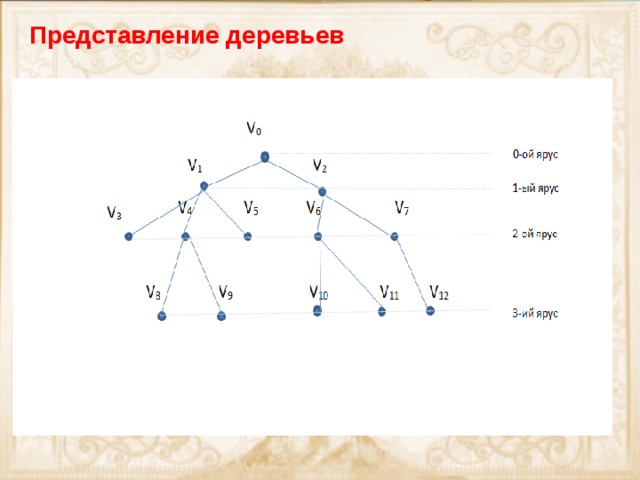
Представление деревьев

Принцип построения : 1. Рисуем «главную» вершину, которая не зависит ни от одной другой вершины (корень дерева или вершина «0 яруса») 2. Добавляем вершины второго яруса (их может быть сколько угодно, все связаны с вершиной 0-го яруса, но не связаны между собой. 3. И.т.д.

Каждая вершина дерева принадлежит ровно одному ярусу.

Номер яруса совпадает с расстоянием между его вершинами и корнем дерева.

Каждая вершина i–го яруса связана ребром ровно с одной вершиной (i-1)-го яруса и не связана ребром ни с какой вершиной i-го яруса.

В дереве любые две вершины соединены единственной цепью (единственный маршрут)

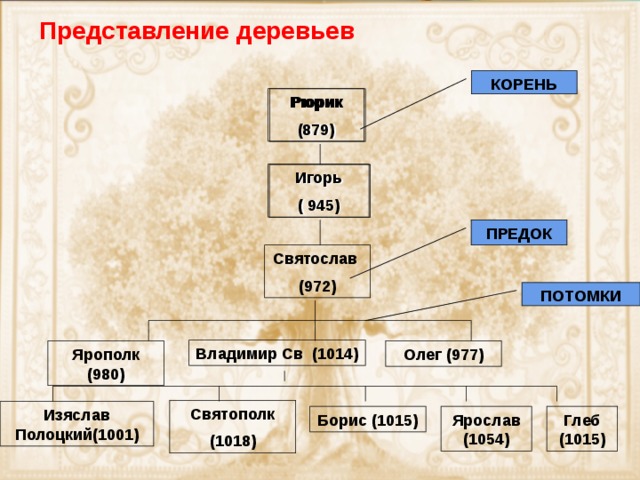
Представление деревьев

КОРЕНЬ

Рюрик

(879)

Рюрик

(879)

Игорь

( 945)

Игорь

( 945)

ПРЕДОК

Святослав

(972)

ПОТОМКИ

Владимир Св (1014)

Олег (977)

Ярополк (980)

Святополк

(1018)

Изяслав Полоцкий(1001)

Глеб (1015)

Ярослав (1054)

Борис (1015)

Дерево

География: население и народное хозяйство России

Введение

Часть1. Общий обзор России

Россия на карте мира

Заселение территории

Сфера влияния России

Экономическое влияние России

Человек и природа

Природные условия и человек

Часть 2. Районы России

Подходы к районированию

Заключение

Иерархическая структура разделов книги

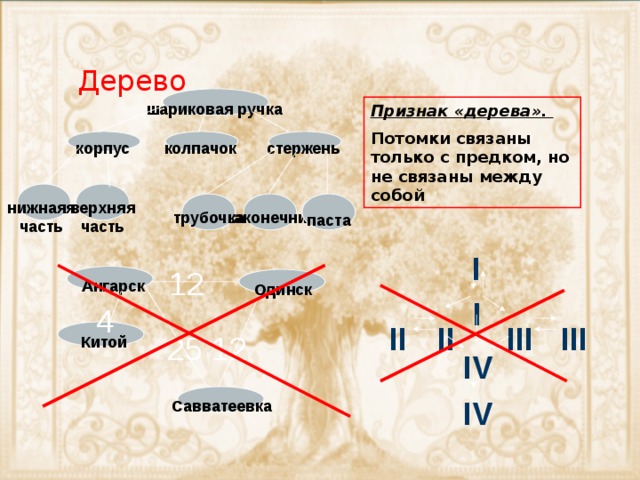
Дерево

шариковая ручка

Признак «дерева».

Потомки связаны только с предком, но не связаны между собой

стержень

корпус

колпачок

нижнаяя

верхняя

часть

часть

наконечник

трубочка

паста

I

12

Ангарск

Одинск

I

4

III

III

II

II

25

12

Китой

IV

IV

Савватеевка

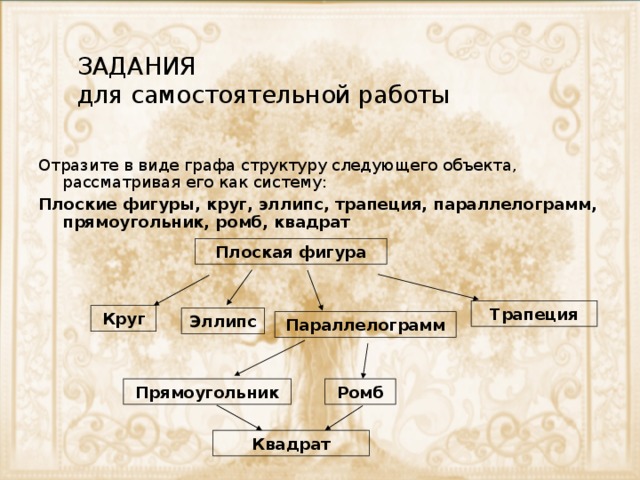
ЗАДАНИЯ для самостоятельной работы

Отразите в виде графа структуру следующего объекта, рассматривая его как систему:

Плоские фигуры, круг, эллипс, трапеция, параллелограмм, прямоугольник, ромб, квадрат

Плоская фигура

Трапеция

Круг

Эллипс

Параллелограмм

Прямоугольник

Ромб

Квадрат

Творческое домашнее задание

А) Представьте в виде графа свою родословную по отцовской линии

Б) Представьте в виде графа свою родословную по материнской линии

УДАЧИ!!!

Лес, остов, бинарное дерево

Упорядоченное объединение непересекающихся деревьев D 1 , D 2 , … , D n представляет собой несвязный граф, называемый ЛЕСом.

Лес, остов, бинарное дерево

Рассмотрим граф G.

1. Будем последовательно удалять циклические ребра до тех пор, пока это будет возможно.

2. В результате получим связный подграф с тем же множеством вершин, но без циклов, то есть получим граф, который называется ОСТОВ данного графа .

ОСТОВ – это любой подграф связного графа, содержащий все вершины графа и являющийся деревом (покрывающим деревом). Ребра остова называются хордами

Остов оформляется в виде таблицы:

ЦИКЛ

[ 1, 9, 14]

УДАЛЯЕМОЕ РЕБРО

[6, 7, 10]

1

6

[5, 13, 14]

5

Спасибо за внимание