2-mavzu. Determinantlar nazariyasi
Reja
Ikkinchi tartibli determinantlar.
Uchinchi tartibli determinantlar.
O’rin almashtirishlar va oʻrinlashtirish.
n-tartibli determinantning ta’rifi va ba’zi bir xossalari.
Tayanch soʻz va iboralar. matritsa, determinant, kvadrat matritsa, aniqlovchi, ikkinchi tartibli determinant, uchinchi tartibli determinant, Sarrius qoidasi, oʻrin almashtirish, oʻrinlashtirish, n-tartibli determinant.
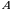 kvadrat matritsaning skalyar (sonli) miqdorini aniqlovchi determinant tushunchasining kiritilishi chiziqli tenglamalar sistemasini yechish bilan chambarchas bogʻliq.
kvadrat matritsaning skalyar (sonli) miqdorini aniqlovchi determinant tushunchasining kiritilishi chiziqli tenglamalar sistemasini yechish bilan chambarchas bogʻliq.
Ikkinchi tartibli determinantlar.
1-ta’rif. Ikkinchi tartibli determinant deb 
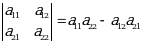 (1)
(1)
tenglik bilan aniqlanadigan songa aytiladi. Qisqacha, Δ deb belgilanadi. Bu yerda 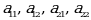 -determinantning elementlari deyiladi.
-determinantning elementlari deyiladi.
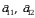 va
va 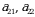 mos ravishda determinantning 1- va 2-satrlari,
mos ravishda determinantning 1- va 2-satrlari, 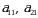 va
va 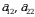 mos ravishda determinantning 1- va 2-ustunlari deyiladi. Ya’ni
mos ravishda determinantning 1- va 2-ustunlari deyiladi. Ya’ni

Determinantning ixtiyoriy satri yoki ustuni determinantning qatori deb ataladi. 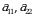 -elementlar joylashgan diagonal bosh diagonal deyiladi.
-elementlar joylashgan diagonal bosh diagonal deyiladi. 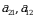 -elementlar joylashgan diagonal yordamchi diagonal deyiladi.
-elementlar joylashgan diagonal yordamchi diagonal deyiladi.
1-misol. Hisoblang: 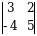
► (1.1.1) formulani qo‘llaymiz:
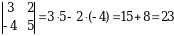 .◄
.◄
Eslatma. Determinantning elementlari funksiyalar bo‘lishi ham mumkin, shuning uchun determinantning qiymati, umuman olganda, funksiyadir.
2-misol.
Hisoblang: 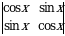 .
.
► 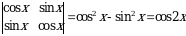 . ◄
. ◄
Uchinchi tartibli determinantlar.
2-ta’rif. Uchinchi tartibli determinant deb
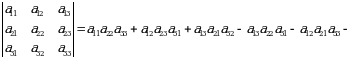
 (2)
(2)
tenglik bilan aniqlanadigan songa aytiladi. Ko‘pincha, determinant tartibiga mos ravishda 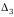 deb ham belgilanadi.
deb ham belgilanadi.
3-misol.
Hisoblang:  .
.
► (1.1.2) formulani qo‘llaymiz:
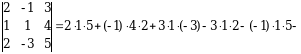
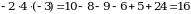 . ◄
. ◄
O’rin almashtirish va oʻrinlashtirish.
Endi biz n-tartibli determinant yoki n-tartibli kvadrat matritsaning determinanti tushunchasini kiritamiz. Bu uchun avval quyidagi yordamchi faktlarni kiritamiz.
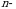 tartibli oʻrin almashtirish tushunchasini kiritamiz.
tartibli oʻrin almashtirish tushunchasini kiritamiz. 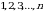 sonlarning biror bir tartibda yozilishi
sonlarning biror bir tartibda yozilishi 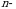 tartibli oʻrin almashtirish deb ataladi.
tartibli oʻrin almashtirish deb ataladi.
3-misol. 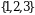 toʻplam uchun barcha oʻrin almashtirishlarni yozing.
toʻplam uchun barcha oʻrin almashtirishlarni yozing.
►
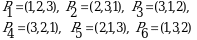
◄
Umuman olganda har qanday  ta elementdan tuzilgan toʻplamda oʻrin almashtirish tushunchasini kiritish mumkin. Bu jarayonni toʻplam elementlarini 1 dan boshlab ketma-ket natural sonlar bilan nomerlaymiz va
ta elementdan tuzilgan toʻplamda oʻrin almashtirish tushunchasini kiritish mumkin. Bu jarayonni toʻplam elementlarini 1 dan boshlab ketma-ket natural sonlar bilan nomerlaymiz va  sonlar ustida oʻrin almashtirishga keltiramiz. Ya’ni,
sonlar ustida oʻrin almashtirishga keltiramiz. Ya’ni,  sonlar ustida oʻrin almashtirish tushunchasini qarash umumiylikni buzmaydi.
sonlar ustida oʻrin almashtirish tushunchasini qarash umumiylikni buzmaydi.
3-ta’rif. Agar 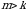 boʻlib,
boʻlib, 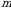 soni
soni 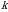 dan chaproqda joylashgan boʻlsa, u holda
dan chaproqda joylashgan boʻlsa, u holda 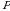 oʻrin almashtirishda
oʻrin almashtirishda 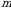 va
va 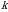 sonlar inversiyani tashkil qiladi deyiladi.
sonlar inversiyani tashkil qiladi deyiladi.
4-ta’rif. 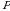 oʻrin almashtirishdagi barcha elementlar tashkil etgan umumiy inversiyalar soni
oʻrin almashtirishdagi barcha elementlar tashkil etgan umumiy inversiyalar soni 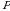 oʻrin almashtirishning inversiyalar soni, deb ataladi va
oʻrin almashtirishning inversiyalar soni, deb ataladi va 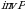 kabi belgilanadi.
kabi belgilanadi.
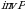 sonning juft yoki toq boʻlishiga qarab, mos ravishda,
sonning juft yoki toq boʻlishiga qarab, mos ravishda, 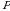 oʻrin almashtirish juft yoki toq deb ataladi.
oʻrin almashtirish juft yoki toq deb ataladi.
Masalan, 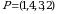 oʻrin almashtirishda 1 va 4 sonlari inversiya tashkil qilmaydi. 3 soniga mos inversiyalar 1 ta, 2 soniga mos inversiyalar 2 ta. Demak,
oʻrin almashtirishda 1 va 4 sonlari inversiya tashkil qilmaydi. 3 soniga mos inversiyalar 1 ta, 2 soniga mos inversiyalar 2 ta. Demak, 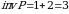 .
. 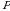 oʻrin almashtirish toq.
oʻrin almashtirish toq.
Oʻrin almashtirish quyidagi xossalarga ega:
1. 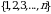 toʻplamdagi barcha oʻrin almashtirishlar soni
toʻplamdagi barcha oʻrin almashtirishlar soni 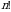 ga teng;
ga teng;
2. Juft va toq oʻrin almashtirishlar soni oʻzaro teng, ya’ni har biri 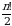 tadan;
tadan;
3. Oʻrin almashtirishda ikkita elementning oʻrni almashtirilsa uning juft-toqligi oʻzgaradi.
5-ta’rif. 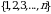 sonlar toʻplamini oʻziga akslantiruvchi, oʻzaro bir qiymatli akslantirish oʻrinlashtirish deb ataladi.
sonlar toʻplamini oʻziga akslantiruvchi, oʻzaro bir qiymatli akslantirish oʻrinlashtirish deb ataladi.
Oʻrinlashtirishni ikkita oʻrin almashtirish bilan berishimiz mumkin. Ikkita 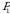 va
va 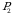
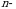 tartibli oʻrin almashtirishlardan tuzilgan
tartibli oʻrin almashtirishlardan tuzilgan 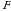 oʻrinlashtirish quyidagicha belgilanadi:
oʻrinlashtirish quyidagicha belgilanadi: 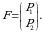
Masalan, 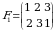 va
va 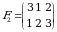 oʻrinlashtirishlar oʻzaro teng. Chunki bu oʻrinlashtirishlarning har biri 1 ga 2 ni, 2 ga 3 ni va 3 ga 1 ni mos qoʻyadi.
oʻrinlashtirishlar oʻzaro teng. Chunki bu oʻrinlashtirishlarning har biri 1 ga 2 ni, 2 ga 3 ni va 3 ga 1 ni mos qoʻyadi.
Shu sababli oʻrinlashtirishni har doim 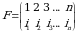 koʻrinishga keltirish mumkin. Bunda
koʻrinishga keltirish mumkin. Bunda 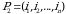 biror
biror 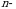 tartibli oʻrin almashtirish.
tartibli oʻrin almashtirish. 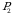 almashtirish juft boʻlsa,
almashtirish juft boʻlsa, 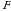 o‘rinlashtirish juft,
o‘rinlashtirish juft, 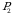 toq boʻlsa,
toq boʻlsa, 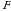 ham toq deyiladi.
ham toq deyiladi. 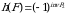 miqdorga
miqdorga 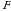 oʻrinlashtirishning signaturasi deyiladi. Demak aniqlanishiga koʻra
oʻrinlashtirishning signaturasi deyiladi. Demak aniqlanishiga koʻra
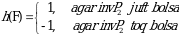
4-misol. Quyidagi orinlashtirishning signaturasini toping.
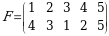
►4 soni soni 3, 1 va 2 sonidan chapda joylashganligi sababli 3 ta inversiya tashkil qiladi, 3 soni soni 1 va 2 sonidan chapda joylashganligi sababli 2 ta inversiya tashkil qiladi, 1, 2 va 5 sonlari inversiya tashkil qilmaydi. Demak 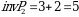 boʻladi. Bundan
boʻladi. Bundan 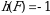 .◄
.◄
5-misol. Quyidagi orinlashtirishning signaturasini toping.
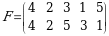
►Birinchi qatorda sonlarni oʻsish tartibida joylashtirib chiqamiz, ya’ni ustunlarning orinlarini almashtiramiz:
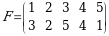
U holda 3 soni soni 1 va 2 sonidan chapda joylashganligi sababli 2 ta inversiya tashkil qiladi, 2 soni soni 1 sonidan chapda joylashganligi sababli 1 ta inversiya tashkil qiladi, 5 soni soni 1 va 4 sonidan chapda joylashganligi sababli 2 ta inversiya tashkil qiladi, 4 soni soni 1 sonidan chapda joylashganligi sababli 1 ta inversiya tashkil qiladi, 1 soni inversiya tashkil qilmaydi. Demak 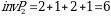 boʻladi. Bundan
boʻladi. Bundan 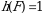 .◄
.◄
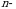 tartibli barcha oʻrinlashtirishlar toʻplamini
tartibli barcha oʻrinlashtirishlar toʻplamini 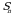 bilan belgilaymiz.
bilan belgilaymiz.
n-tartibli determinantning ta’rifi va ba’zi bir xossalari.
Endi 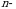 tartibli determinant tushunchasini kiritamiz. Bizga
tartibli determinant tushunchasini kiritamiz. Bizga 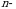 tartibli
tartibli
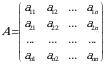
kvadrat matritsa berilgan boʻlsin.
6-ta’rif. Barcha mumkin boʻlgan turli 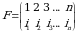 oʻrinlashtirishlarga mos
oʻrinlashtirishlarga mos 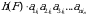 koʻrinishdagi n! ta koʻpaytmalarning yig‘indisidan iborat songa
koʻrinishdagi n! ta koʻpaytmalarning yig‘indisidan iborat songa 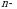 tartibli determinant deyiladi.
tartibli determinant deyiladi.
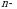 tartibli determinant
tartibli determinant 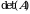 ,
, 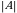 yoki
yoki 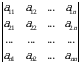
kabi belgilanadi.
Oʻrinlashtirish va oʻrin almashtirishlarning xossalariga asosan, bu ta’rifdan:
1) 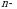 tartibli determinant
tartibli determinant 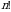 ta hadning yig‘indisidan iborat;
ta hadning yig‘indisidan iborat;
2) bu yig‘indining har bir hadi matritsaning turli satrlari va turli ustunlarida joylashgan  ta elementi koʻpaytmasidan iborat, ya’ni yig‘indining har bir hadida, har bir satrdan va har bir ustundan yagona element qatnashadi.
ta elementi koʻpaytmasidan iborat, ya’ni yig‘indining har bir hadida, har bir satrdan va har bir ustundan yagona element qatnashadi.
3) yuqorida aytilgan koʻpaytmalarning yarmi (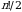 tasi) oʻz ishorasi bilan, qolgan yarmi qarama-qarshi ishora bilan olingan.
tasi) oʻz ishorasi bilan, qolgan yarmi qarama-qarshi ishora bilan olingan.
6-misol. Quyidagi koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasini aniqlaydimi, agar aniqlasa bu qoʻshiluvchining ishorasini toping.
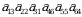
►Ta’rifga ko‘ra, yig‘indining har bir hadida, har bir satrdan va har bir ustundan yagona element qatnashadi. Birinchi indeksda qatnashayotgan sonlar har xil va 1 dan 6 gacha (1,2,3,4,5,6), ikkinchi indeksda qatnashayotgan sonlar ham har xil va 1 dan 6 gacha (1,2,3,4,5,6). Bundan bu ko‘paytma 6-tartibli determinantning biror hadini bildirishi kelib chiqadi. Bu handing ishorasini topish uchun quyidagi o‘rinlashtirishni tuzamiz:
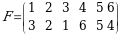
U holda 3 soni 1 va 2 sonidan chapda joylashganligi sababli 2 ta inversiya tashkil qiladi, 2 soni 1 sonidan chapda joylashganligi sababli 1 ta inversiya tashkil qiladi, 6 soni 5 va 4 sonidan chapda joylashganligi sababli 2 ta inversiya tashkil qiladi, 5 soni 4 sonidan chapda joylashganligi sababli 1 ta inversiya tashkil qiladi, 1 soni inversiya tashkil qilmaydi. Demak 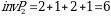 boʻladi. Bundan
boʻladi. Bundan 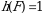 va bu handing ishorasi ko‘paytmaning ishorasi bilan bir xil bo‘ladi.◄
va bu handing ishorasi ko‘paytmaning ishorasi bilan bir xil bo‘ladi.◄
7-misol. Quyidagi koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasini aniqlaydimi, agar aniqlasa bu qoʻshiluvchining ishorasini toping.
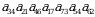
►Bu ko‘paytmadagi 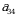 va
va 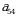 elementlar ikkalasi ham 4-ustunga tegishli, n-tartibli determinantning ta’rifiga ko‘ra yig‘indining har bir qo‘shiluvchisida, har bir satrdan va har bir ustundan yagona element qatnashishi kerak. Demak bu koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasi bo‘la olmaydi.◄
elementlar ikkalasi ham 4-ustunga tegishli, n-tartibli determinantning ta’rifiga ko‘ra yig‘indining har bir qo‘shiluvchisida, har bir satrdan va har bir ustundan yagona element qatnashishi kerak. Demak bu koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasi bo‘la olmaydi.◄
Biz yuqorida koʻrgan 2-tartibli kvadrat matritsaning determinantini n-tartibli determinantning t’rifidan foydalanib hisoblaymiz:
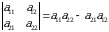 .
.
Haqiqatan, ikkinchi tartibli turli oʻrinlashtirishlar soni 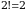 ta. Bular
ta. Bular
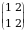 va
va 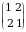 .
.
Bulardan birinchisi juft, ikkinchisi esa toq. Shu sababli determinant 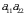 va
va 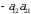 sonlarning yig‘indisidan iborat.
sonlarning yig‘indisidan iborat.
Endi uchinchi tartibli determinantni qaraymiz. Uchinchi tartibli turli oʻrinlashtirishlar soni 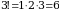 ta. Bular
ta. Bular
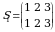 ,
, 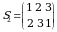 ,
, 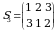 ,
,
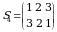 ,
, 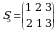 ,
, 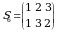 .
.
Bu oʻrinlashtirishlarning ikkinchi satridagi oʻrin almashtirishlarni qaraymiz. 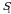 da
da 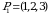 boʻlib,
boʻlib, 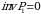 ,
, 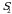 da
da 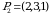 boʻlib,
boʻlib, 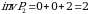 ,
, 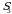 da
da 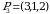 boʻlib,
boʻlib, 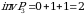 . Demak,
. Demak, 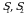 va
va 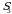 lar juft boʻlib, ularga mos signaturalar 1 ga teng. Shu sababli determinantni ifodalovchi yig‘indida bu uchta oʻrinlashtirishga mos
lar juft boʻlib, ularga mos signaturalar 1 ga teng. Shu sababli determinantni ifodalovchi yig‘indida bu uchta oʻrinlashtirishga mos 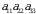 ,
, 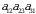 va
va 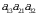 koʻpaytmalar oʻz ishorasi bilan olinadi. Juft va toq oʻrin almashtirishlar soni teng boʻlganligi sababli, qolgan uchta
koʻpaytmalar oʻz ishorasi bilan olinadi. Juft va toq oʻrin almashtirishlar soni teng boʻlganligi sababli, qolgan uchta 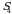 ,
, 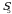 va
va 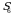 lar toq va ularga mos
lar toq va ularga mos 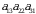 ,
, 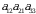 va
va 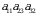 koʻpaytmalar qarama-qarshi ishora bilan olinishi kerak.
koʻpaytmalar qarama-qarshi ishora bilan olinishi kerak.
Yuqoridagilarni umumlashtirsak, uchinchi tartibli determinant uchun quyidagi ifodani olamiz:
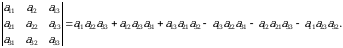
Bundan koʻrinib turibdiki, determinantni ta’rif boʻyicha hisoblash juda koʻp amallardan iborat boʻlib, ma’lum noqulayliklarga ega. Misol uchun 4-tartibli determinant 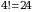 ta haddan iborat. Har bir hadi matritsaning turli satr va ustunlaridan olingan 4 ta elementi koʻpaytmasidan iborat. Bu hadlarning har birining ishorasini topish uchun 24 ta oʻrinlashtirishning juft-toqligi aniqlanishi talab qilinadi.
ta haddan iborat. Har bir hadi matritsaning turli satr va ustunlaridan olingan 4 ta elementi koʻpaytmasidan iborat. Bu hadlarning har birining ishorasini topish uchun 24 ta oʻrinlashtirishning juft-toqligi aniqlanishi talab qilinadi.
Shu sababdan determinantni uning ba’zi xossalaridan foydalanib hisoblash qulayroq.
Bugungi ma’ruzamizda determinantning ba’zi bir xossalarini koʻramiz.
1-xossa. Agar determinant biror satri (yoki ustuni) ning barcha elementlari nolga  teng boʻlsa, u holda uning qiymati nolga teng boʻladi.
teng boʻlsa, u holda uning qiymati nolga teng boʻladi.
Bu xossa bevosita ta’rifdan kelib chiqadi, chunki determunantni aniqlovchi yigindining har bir qoshiluvchisida bu qatorning (yoki ustunning) albatta bitta elementi kopaytuvchi sifatida qatnashadi.
Masalan,
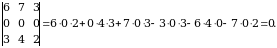
2-xossa. Diagonal matritsaning determinanti diagonal elementlarining koʻpaytmasiga teng, ya’ni:
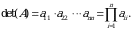
3-xossa. Yuqori (quyi) uchburchakli matritsalarning determinantlari uning bosh diagonal elementlari koʻpaytmasiga teng, ya’ni:
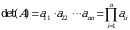 .
.
Masalan,
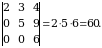
4-xossa. Determinantning biror satri (ustuni) elementlarini 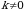 songa koʻpaytirish determinantni shu songa koʻpaytirishga teng kuchlidir yoki biror satr (ustun) elementlarining umumiy koʻpaytuvchisini determinant belgisidan tashqariga chiqarish mumkin, ya’ni:
songa koʻpaytirish determinantni shu songa koʻpaytirishga teng kuchlidir yoki biror satr (ustun) elementlarining umumiy koʻpaytuvchisini determinant belgisidan tashqariga chiqarish mumkin, ya’ni:
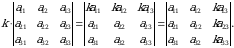
Masalan,
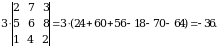
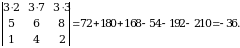
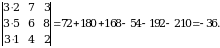
5-xossa. 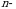 tartibli determinant uchun quyidagi tenglik oʻrinli:
tartibli determinant uchun quyidagi tenglik oʻrinli:
O‘z-o‘zini tekshirish uchun savollar
Uchinchi tartibli determinant deb nimaga aytiladi?
Uchinchi tartibli determinantni hisoblash Sarrus qoidasi nimadan iborat?
Uchinchi tartibli determinantni hisoblash uchburchak sxemasini yozing.
Transpozitsiyalash deganda nimani tushunasiz?
Juft yoki toq o’rin almashtirish tizimi deb, qanday o’rin almashtirishga aytiladi?
n-tartibli determinant deb nimaga aytiladi?
Asosiy adabiyotlar:
Gilbert Strang “Introduction to Linear Algebra”, USA, Cambridge press,  Edition, 2016.
Edition, 2016.
Grewal B.S. “Higher Engineering Mathematics”, Delhi, Khanna publishers,  Edition, 2012.
Edition, 2012.
Raxmatov R.R., Adizov A.A., Tadjibayeva Sh.E., Shoimardonov S.K. Chiziqli algebra va analitik geometriya. O‘quv qollanma. Toshkent 2020.
Rаxмаtоv R.R., Adizov A.A. “Chiziqli fazo va chiziqli operatorlar” O‘quv uslubiy qollanma. TATU, Toshkent 2019.
Соатов Ё.У. “Олий математика”, Т., Ўқитувчи нашриёти, 1- 5 қисмлар, 1995.
Рябушко А.П. и др. “Сборник индивидуальных заданий по высшей математике”, Минск, Высшая школа, 1-3 частях, 1991.
Asosiy adabiyotlar:
Мирзиёев Ш. Буюк келажагимизни мард ва олижаноб халқимиз билан бирга қурамиз. –Т.: Ўзбекистон, 2017. - 488 бет.
Мирзиёев Ш.М. Қонун устуворлиги ва инсон манфаатларини таъминлаш-юрт тараққиёти ва халқ фаровонлигининг гарови. –Т.: Ўзбекистон, 2017.
Мирзиёев Ш.М. Эркин ва фаровон, демократик Ўзбекистон давлатини биргаликда барпо этамиз. Т.: Ўзбекистон, 2017.
Adizov A.A., Xudoyberganov M.O‘. Amaliy matematika. O‘quv uslubiy qo‘llanma. Toshkent. 2014.
Шодиев Т.Ш. Аналитик геометрия ва чизиқли алгебра. Тошкент “Ўқитувчи” 1984.
Ильин В. А., Позняк Э. Г. Линейная алгебра. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004.
Задорожный В. Н. и др. Высшая математика для технических
университетов. Часть I. Линейная алгебра. - Томск: Изд-во ТПУ, 2009.
Данко П.С., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Седьмое издание. -М.: Высшая; школа, 2015.
Семёнова Т.В. Высшая математика: учебное пособие для студентов технических вузов. Часть 1. - Пенза: Пензенский гос. ун-т, 2008.
Макаров Е. В., Лунгу К. Н. Высшая математика: руководство к решению задач: учебное пособие, Часть 1, Физматлит. 2013.
Минорский В.И. Сборник задач по высшей математике. М: Наука, 1987.
Беклемишев Д.В., Петрович А.Ю., Чуберов И.А. Сборник задач по аналитической геометрии и линейной алгебре. -М.: Наука, 1987.
Бугров Я.С., Николский С.М. Сборник задач по высшей математике, - М.: Наука. 1997.







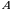 kvadrat matritsaning skalyar (sonli) miqdorini aniqlovchi determinant tushunchasining kiritilishi chiziqli tenglamalar sistemasini yechish bilan chambarchas bogʻliq.
kvadrat matritsaning skalyar (sonli) miqdorini aniqlovchi determinant tushunchasining kiritilishi chiziqli tenglamalar sistemasini yechish bilan chambarchas bogʻliq.
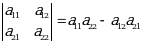 (1)
(1)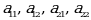 -determinantning elementlari deyiladi.
-determinantning elementlari deyiladi. 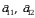 va
va 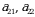 mos ravishda determinantning 1- va 2-satrlari,
mos ravishda determinantning 1- va 2-satrlari, 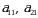 va
va 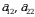 mos ravishda determinantning 1- va 2-ustunlari deyiladi. Ya’ni
mos ravishda determinantning 1- va 2-ustunlari deyiladi. Ya’ni
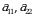 -elementlar joylashgan diagonal bosh diagonal deyiladi.
-elementlar joylashgan diagonal bosh diagonal deyiladi. 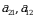 -elementlar joylashgan diagonal yordamchi diagonal deyiladi.
-elementlar joylashgan diagonal yordamchi diagonal deyiladi.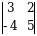
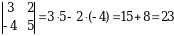 .◄
.◄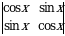 .
.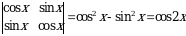 . ◄
. ◄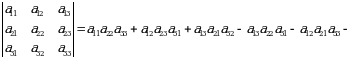
 (2)
(2)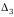 deb ham belgilanadi.
deb ham belgilanadi. .
.
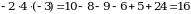 . ◄
. ◄ tartibli oʻrin almashtirish tushunchasini kiritamiz.
tartibli oʻrin almashtirish tushunchasini kiritamiz. 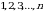 sonlarning biror bir tartibda yozilishi
sonlarning biror bir tartibda yozilishi 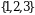 toʻplam uchun barcha oʻrin almashtirishlarni yozing.
toʻplam uchun barcha oʻrin almashtirishlarni yozing.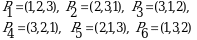
 ta elementdan tuzilgan toʻplamda oʻrin almashtirish tushunchasini kiritish mumkin. Bu jarayonni toʻplam elementlarini 1 dan boshlab ketma-ket natural sonlar bilan nomerlaymiz va
ta elementdan tuzilgan toʻplamda oʻrin almashtirish tushunchasini kiritish mumkin. Bu jarayonni toʻplam elementlarini 1 dan boshlab ketma-ket natural sonlar bilan nomerlaymiz va 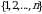 sonlar ustida oʻrin almashtirishga keltiramiz. Ya’ni,
sonlar ustida oʻrin almashtirishga keltiramiz. Ya’ni,  boʻlib,
boʻlib,  soni
soni 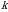 dan chaproqda joylashgan boʻlsa, u holda
dan chaproqda joylashgan boʻlsa, u holda 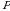 oʻrin almashtirishda
oʻrin almashtirishda 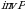 kabi belgilanadi.
kabi belgilanadi.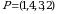 oʻrin almashtirishda 1 va 4 sonlari inversiya tashkil qilmaydi. 3 soniga mos inversiyalar 1 ta, 2 soniga mos inversiyalar 2 ta. Demak,
oʻrin almashtirishda 1 va 4 sonlari inversiya tashkil qilmaydi. 3 soniga mos inversiyalar 1 ta, 2 soniga mos inversiyalar 2 ta. Demak, 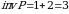 .
. 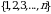 toʻplamdagi barcha oʻrin almashtirishlar soni
toʻplamdagi barcha oʻrin almashtirishlar soni 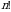 ga teng;
ga teng;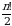 tadan;
tadan;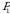 va
va 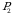
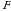 oʻrinlashtirish quyidagicha belgilanadi:
oʻrinlashtirish quyidagicha belgilanadi: 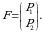
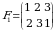 va
va 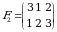 oʻrinlashtirishlar oʻzaro teng. Chunki bu oʻrinlashtirishlarning har biri 1 ga 2 ni, 2 ga 3 ni va 3 ga 1 ni mos qoʻyadi.
oʻrinlashtirishlar oʻzaro teng. Chunki bu oʻrinlashtirishlarning har biri 1 ga 2 ni, 2 ga 3 ni va 3 ga 1 ni mos qoʻyadi.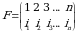 koʻrinishga keltirish mumkin. Bunda
koʻrinishga keltirish mumkin. Bunda 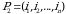 biror
biror 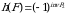 miqdorga
miqdorga 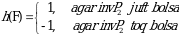
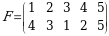
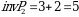 boʻladi. Bundan
boʻladi. Bundan 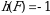 .◄
.◄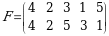
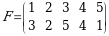
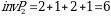 boʻladi. Bundan
boʻladi. Bundan 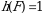 .◄
.◄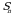 bilan belgilaymiz.
bilan belgilaymiz.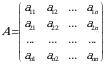
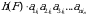 koʻrinishdagi n! ta koʻpaytmalarning yig‘indisidan iborat songa
koʻrinishdagi n! ta koʻpaytmalarning yig‘indisidan iborat songa 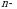 tartibli determinant deyiladi.
tartibli determinant deyiladi.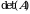 ,
, 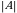 yoki
yoki 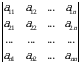
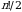 tasi) oʻz ishorasi bilan, qolgan yarmi qarama-qarshi ishora bilan olingan.
tasi) oʻz ishorasi bilan, qolgan yarmi qarama-qarshi ishora bilan olingan.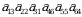
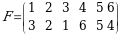
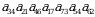
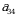 va
va 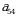 elementlar ikkalasi ham 4-ustunga tegishli, n-tartibli determinantning ta’rifiga ko‘ra yig‘indining har bir qo‘shiluvchisida, har bir satrdan va har bir ustundan yagona element qatnashishi kerak. Demak bu koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasi bo‘la olmaydi.◄
elementlar ikkalasi ham 4-ustunga tegishli, n-tartibli determinantning ta’rifiga ko‘ra yig‘indining har bir qo‘shiluvchisida, har bir satrdan va har bir ustundan yagona element qatnashishi kerak. Demak bu koʻpaytma birorta determinantni aniqlovchi yigʻindining qoʻshiluvchilaridan birortasi bo‘la olmaydi.◄ 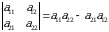 .
.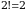 ta. Bular
ta. Bular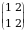 va
va 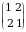 .
.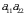 va
va 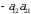 sonlarning yig‘indisidan iborat.
sonlarning yig‘indisidan iborat.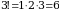 ta. Bular
ta. Bular 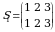 ,
, 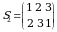 ,
, 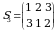 ,
,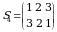 ,
, 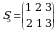 ,
, 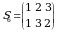 .
.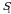 da
da 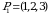 boʻlib,
boʻlib, 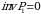 ,
, 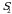 da
da 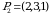 boʻlib,
boʻlib, 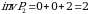 ,
, 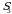 da
da 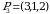 boʻlib,
boʻlib, 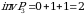 . Demak,
. Demak, 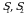 va
va 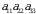 ,
, 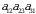 va
va 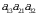 koʻpaytmalar oʻz ishorasi bilan olinadi. Juft va toq oʻrin almashtirishlar soni teng boʻlganligi sababli, qolgan uchta
koʻpaytmalar oʻz ishorasi bilan olinadi. Juft va toq oʻrin almashtirishlar soni teng boʻlganligi sababli, qolgan uchta 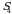 ,
, 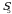 va
va 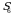 lar toq va ularga mos
lar toq va ularga mos 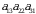 ,
, 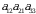 va
va 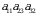 koʻpaytmalar qarama-qarshi ishora bilan olinishi kerak.
koʻpaytmalar qarama-qarshi ishora bilan olinishi kerak. 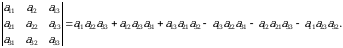
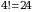 ta haddan iborat. Har bir hadi matritsaning turli satr va ustunlaridan olingan 4 ta elementi koʻpaytmasidan iborat. Bu hadlarning har birining ishorasini topish uchun 24 ta oʻrinlashtirishning juft-toqligi aniqlanishi talab qilinadi.
ta haddan iborat. Har bir hadi matritsaning turli satr va ustunlaridan olingan 4 ta elementi koʻpaytmasidan iborat. Bu hadlarning har birining ishorasini topish uchun 24 ta oʻrinlashtirishning juft-toqligi aniqlanishi talab qilinadi. teng boʻlsa, u holda uning qiymati nolga teng boʻladi.
teng boʻlsa, u holda uning qiymati nolga teng boʻladi. 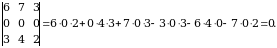
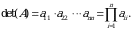
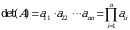 .
.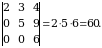
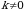 songa koʻpaytirish determinantni shu songa koʻpaytirishga teng kuchlidir yoki biror satr (ustun) elementlarining umumiy koʻpaytuvchisini determinant belgisidan tashqariga chiqarish mumkin, ya’ni:
songa koʻpaytirish determinantni shu songa koʻpaytirishga teng kuchlidir yoki biror satr (ustun) elementlarining umumiy koʻpaytuvchisini determinant belgisidan tashqariga chiqarish mumkin, ya’ni: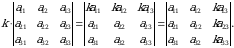
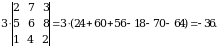
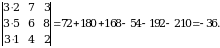
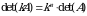
 Edition, 2016.
Edition, 2016.  Edition, 2012.
Edition, 2012. 









