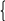| № | Содержание материала | Практические задания | Ответы |
|
1 |
Функция. Область определения и область значений функции | 1). Функция задана формулой 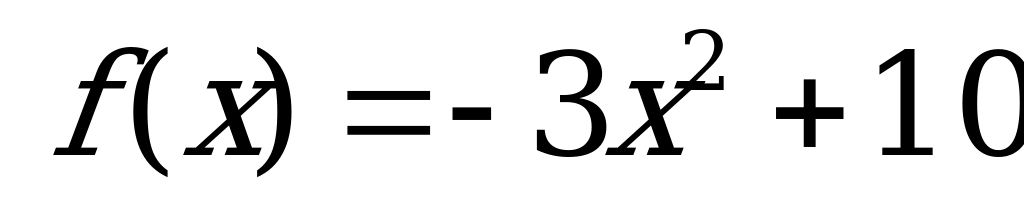 . Найди: . Найди: а) 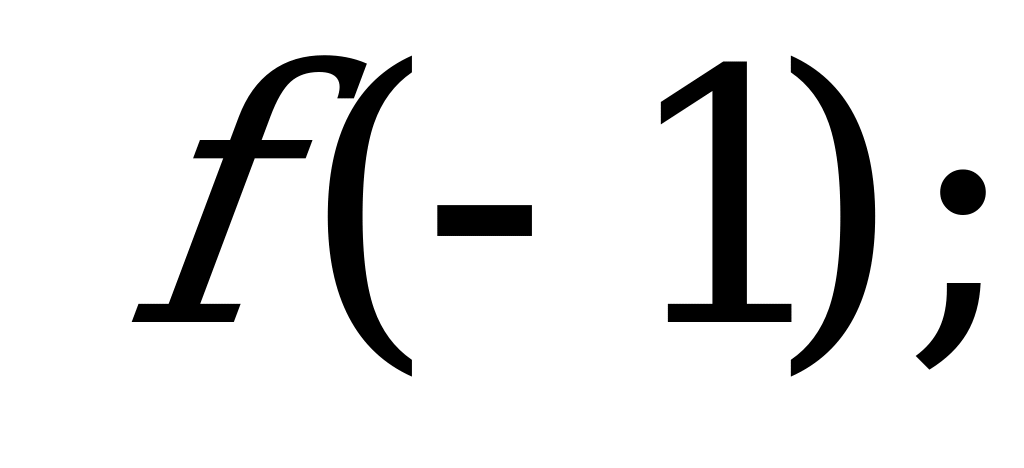 б) б) 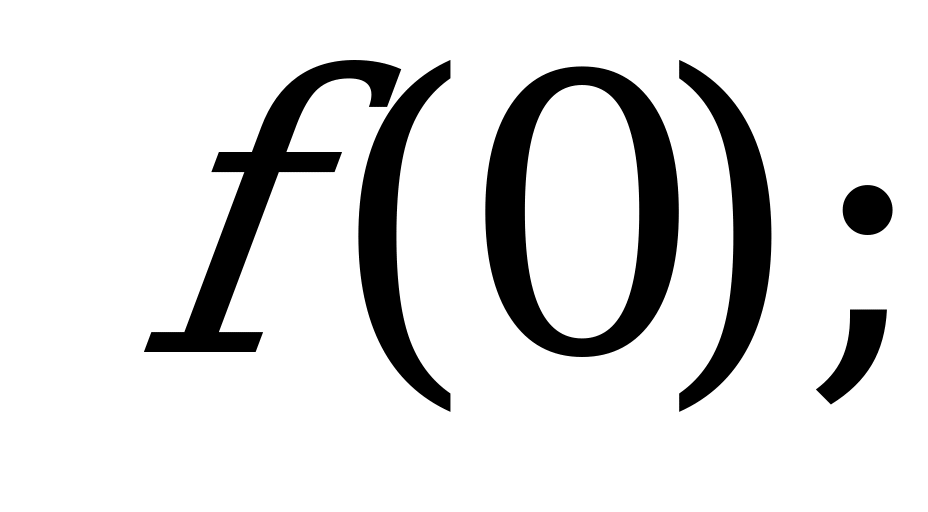 в) в) 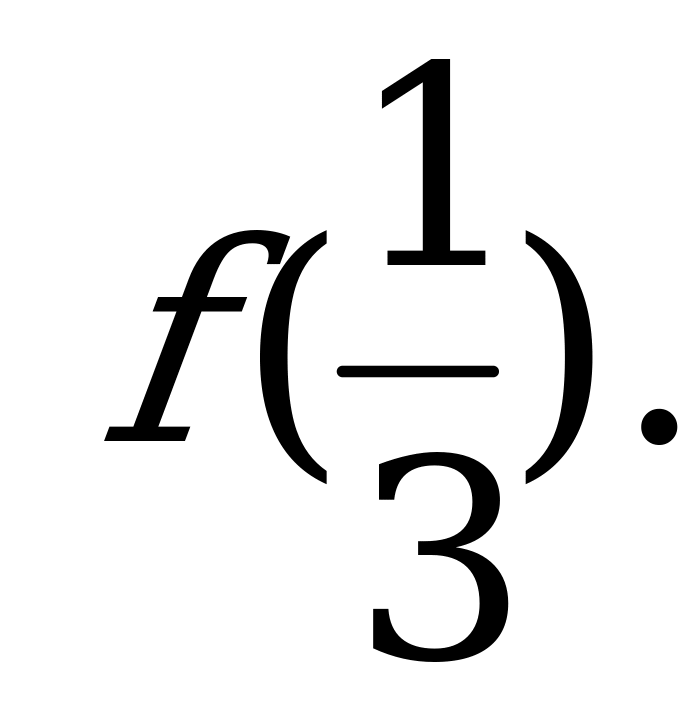 2). Найдите область определения функции, заданной формулой: а)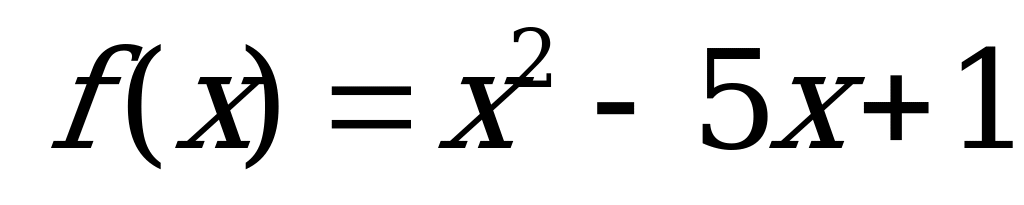 ; б) ; б)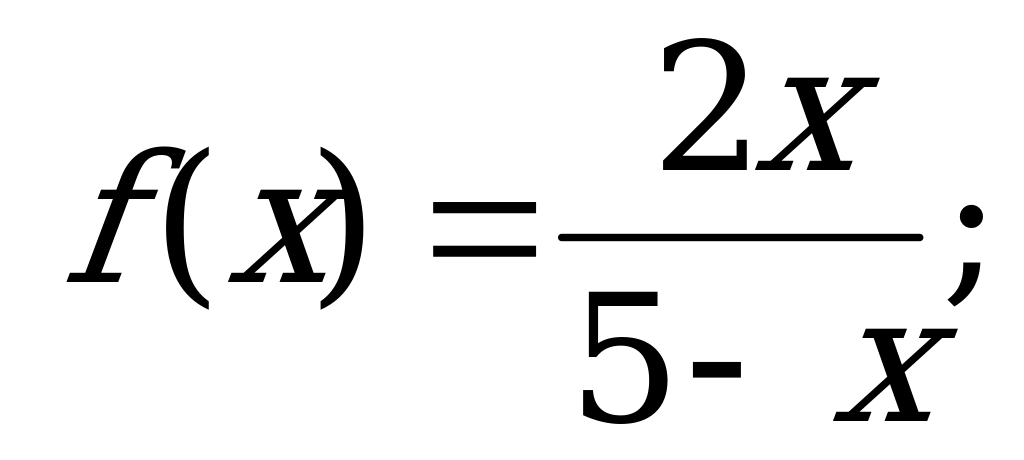 в) в)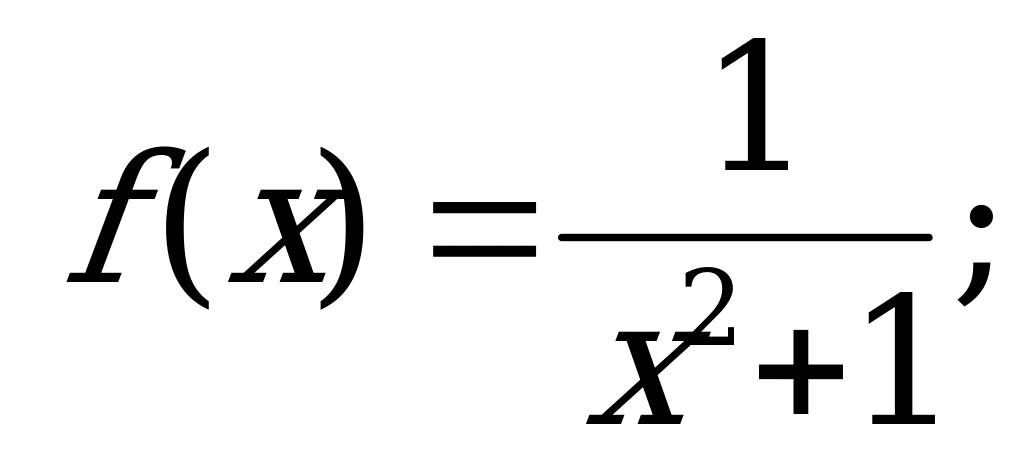 г) г) 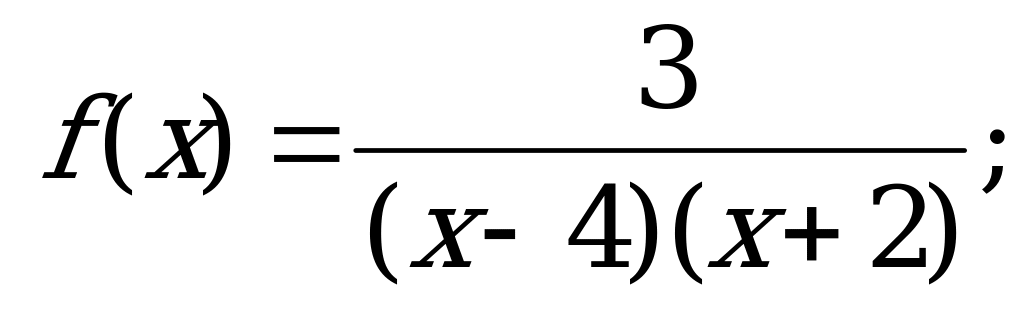 д) д) 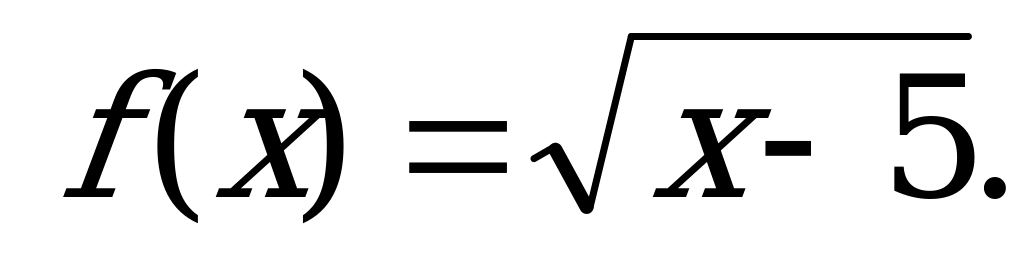 |
|
|
2 |
Свойства функции | 1). Найдите нули функции: а)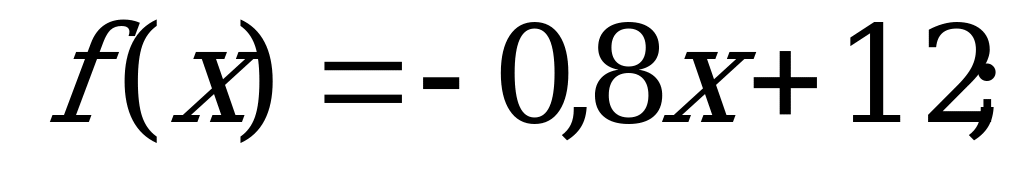 б) б) 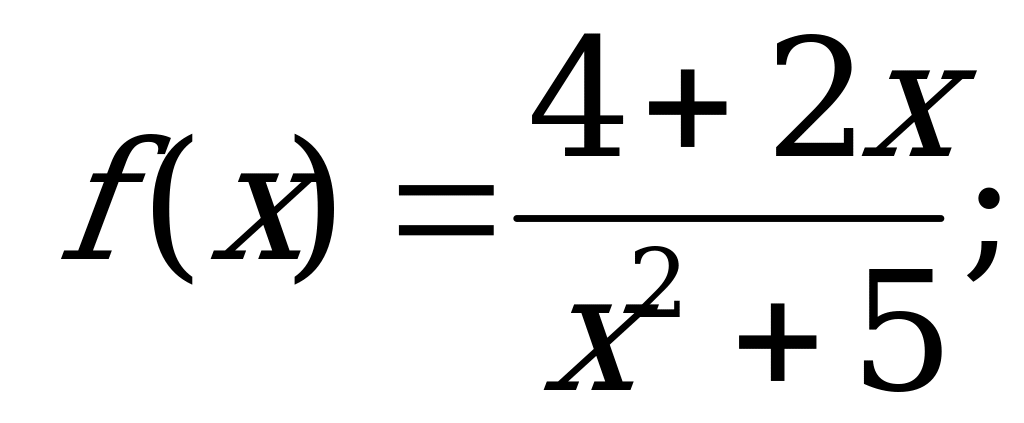 в) в) 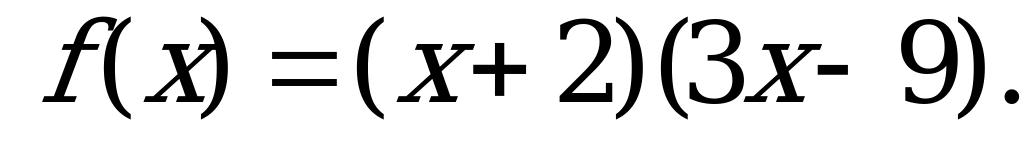 2). Функция заданна формулой 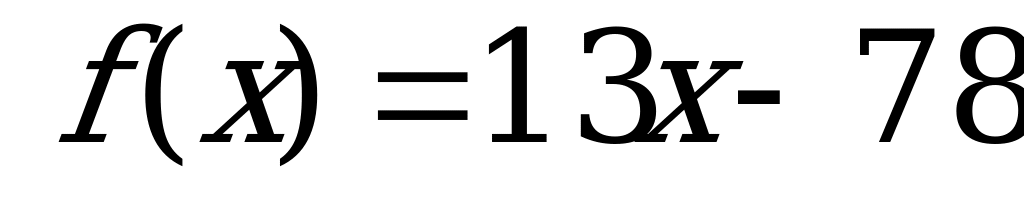 . При каких значениях х: а) . При каких значениях х: а) 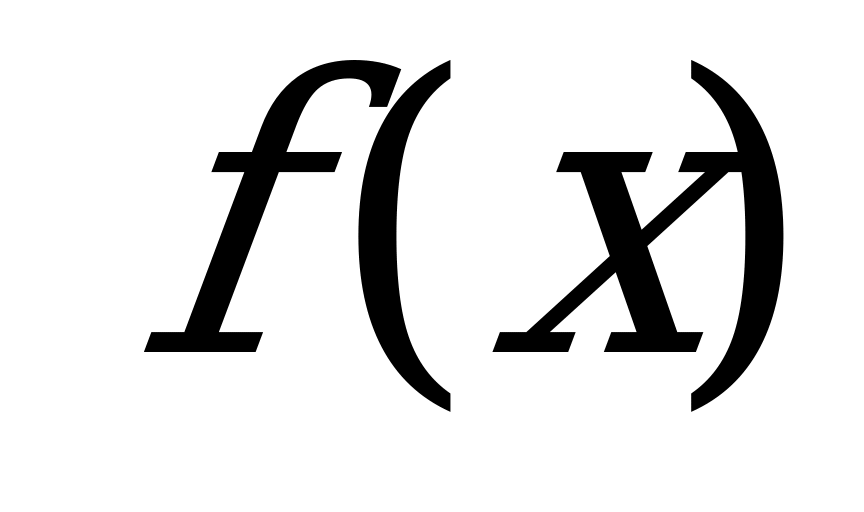 0; б) 0; б) 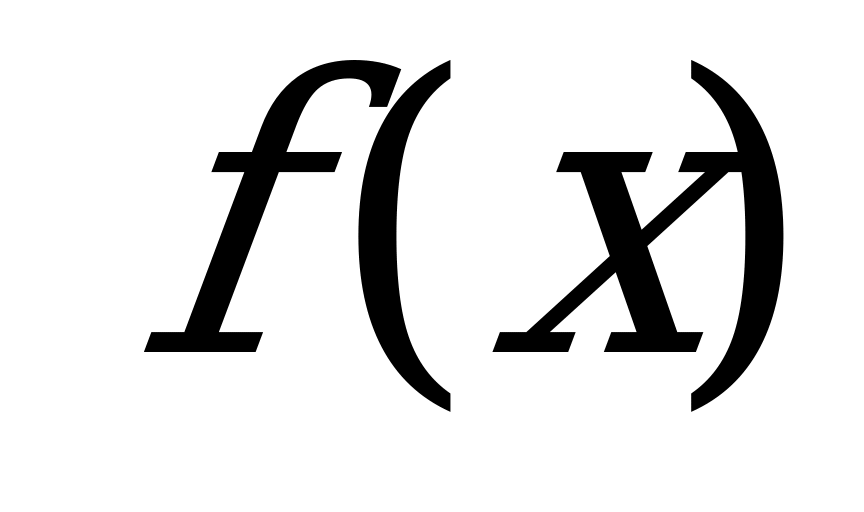 |
|
|
3 |
Квадратный трехчлен и его корни | Имеет ли квадратный трехчлен корни, и если имеет, то сколько: а) 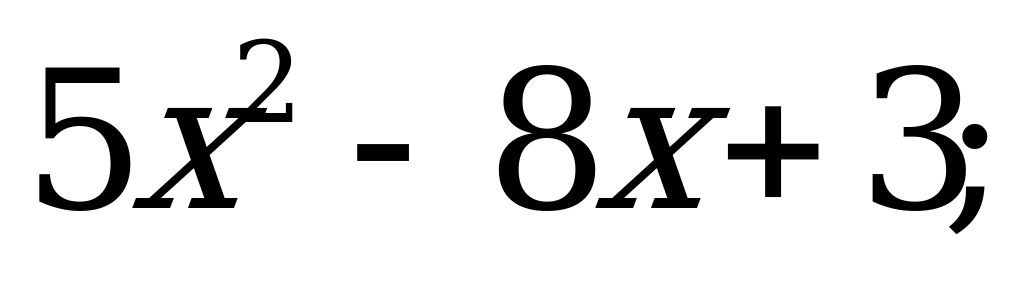 б) б) 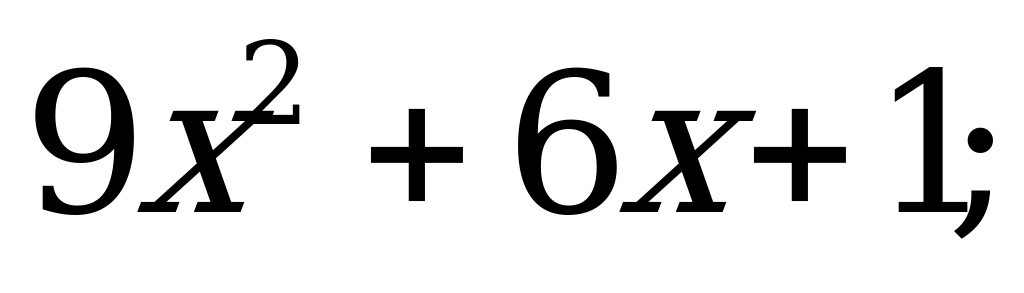 в) в) 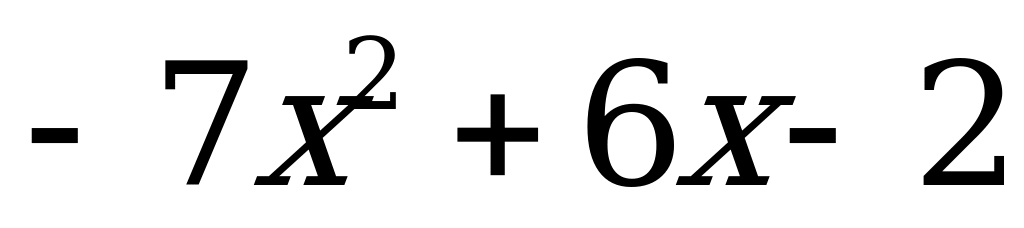 ? ?
|
|
|
4 |
Разложение квадратного трехчлена на множители | 1). Разложите на множители квадратный трехчлен: а) 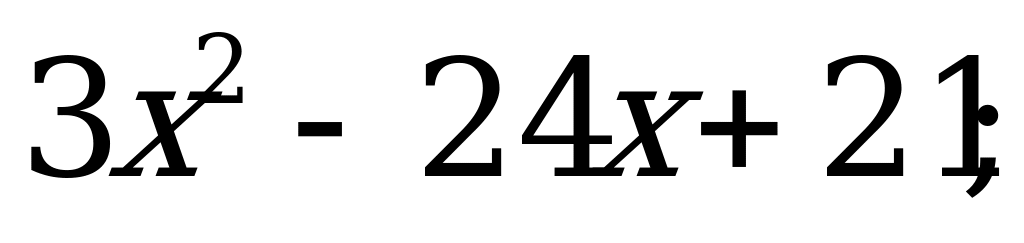 б) б) 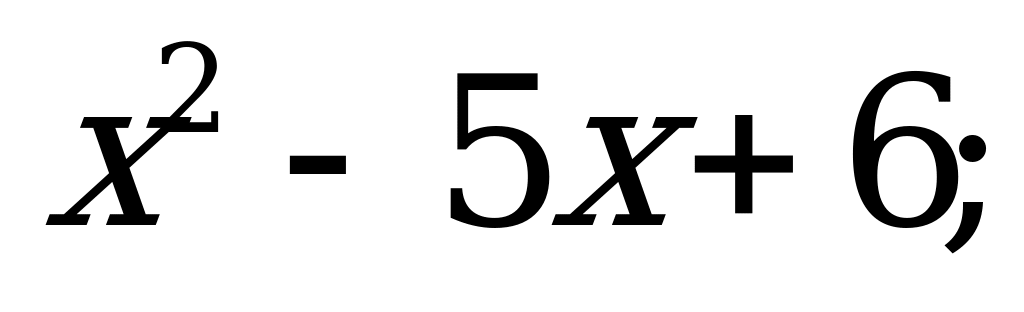 в) в) 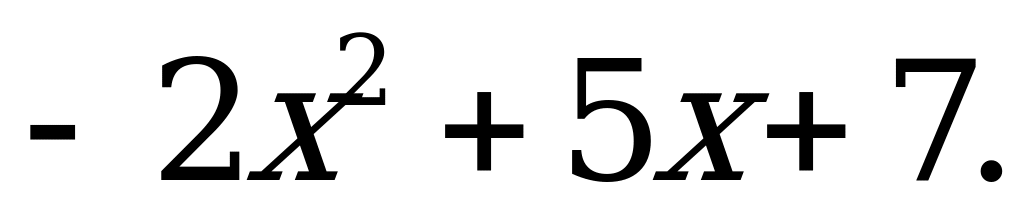 2). Сократите дробь: а) 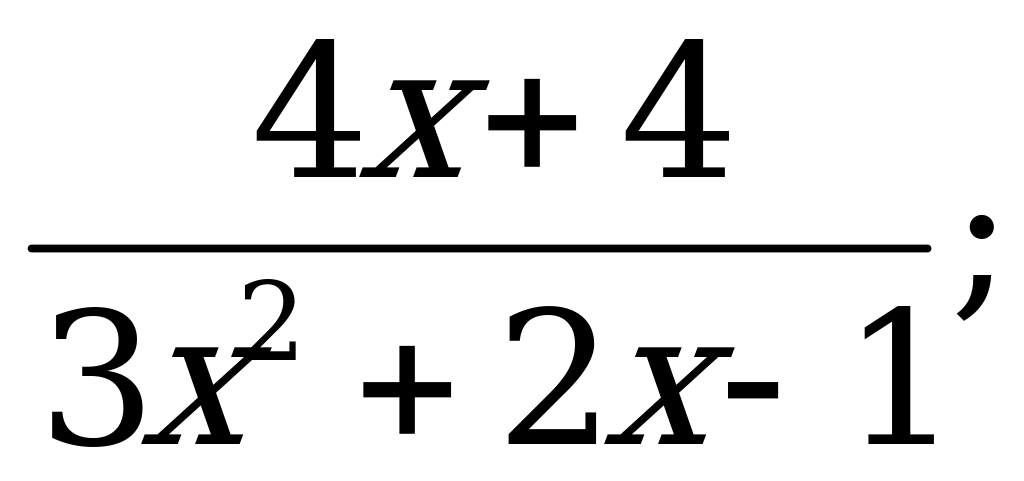 б) б) 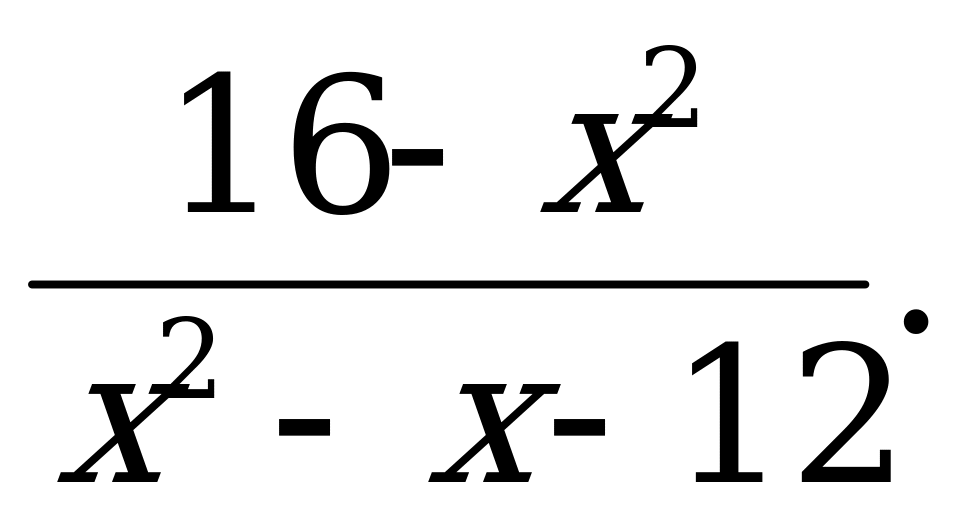
|
|
|
5 |
Построение графика квадратичной функции | Постройте график функции 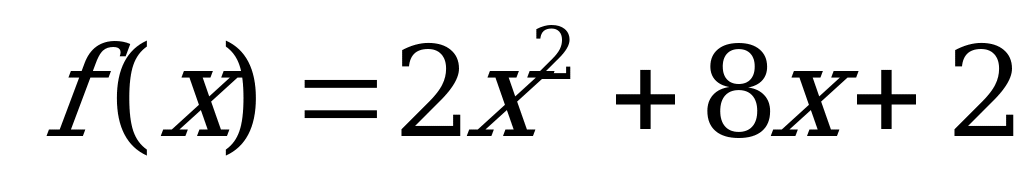 и найди, используя график : а) нули функции; б) промежутки, в которых и найди, используя график : а) нули функции; б) промежутки, в которых 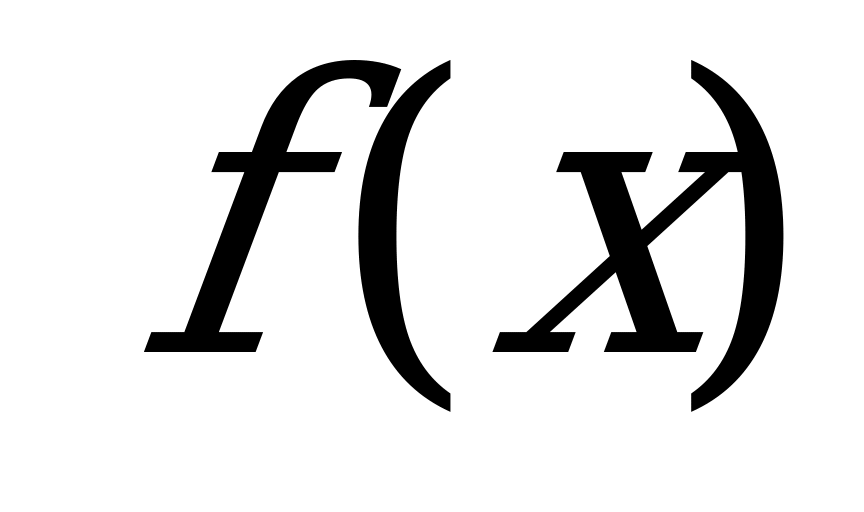 0, 0, 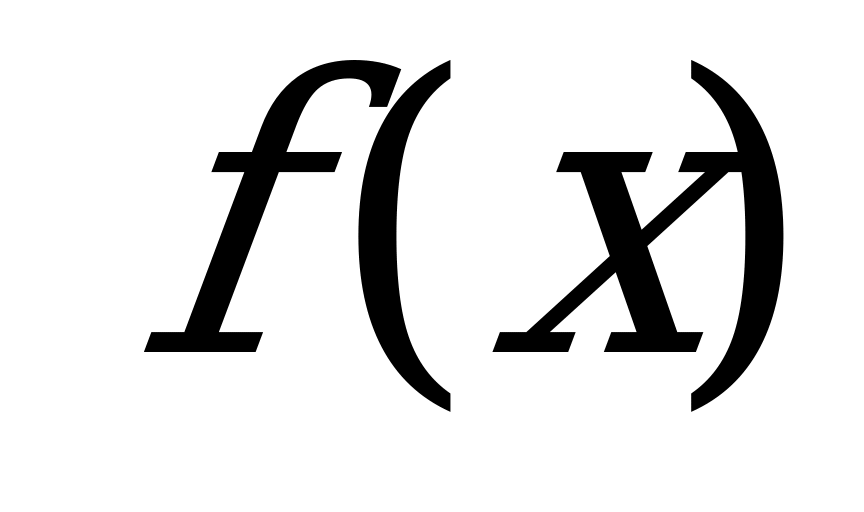 функции; г) наименьшее значение функции. функции; г) наименьшее значение функции. |
|
| № | Содержание материала | Практические задания |
|
|
6
|
Решение неравенств второй степени с одной переменной | Решите неравенство: а) 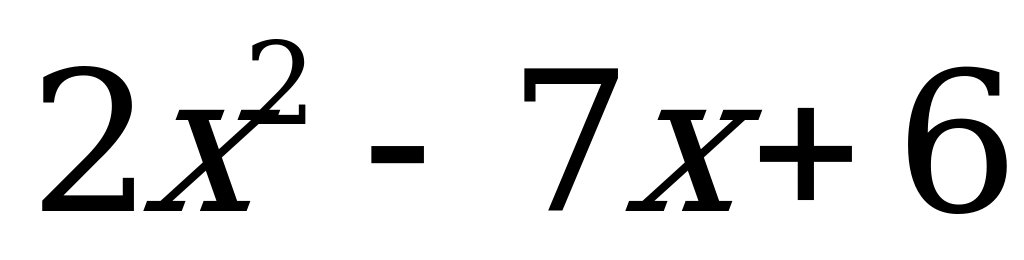 0; б) 0; б) 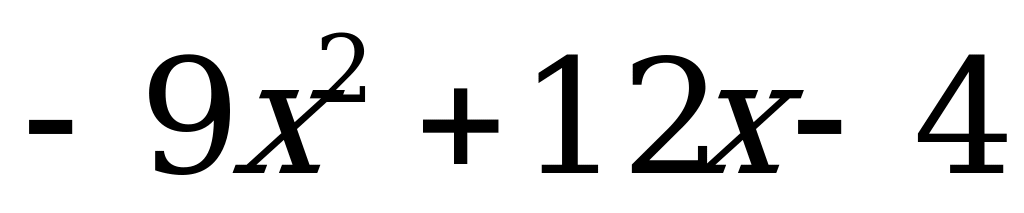 в) 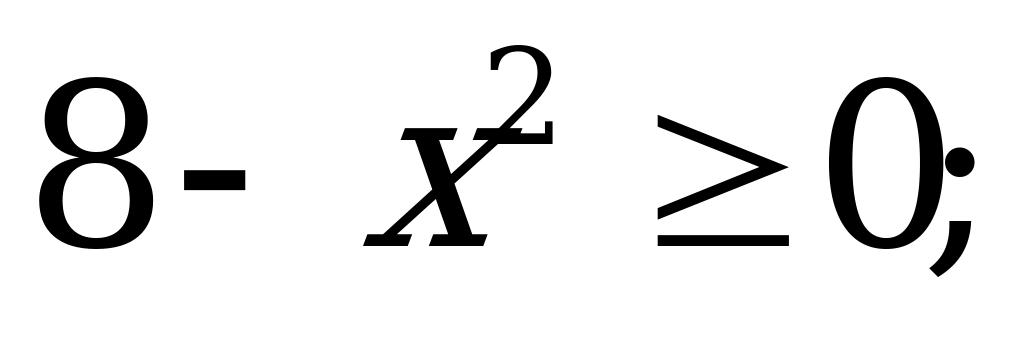 г) г) 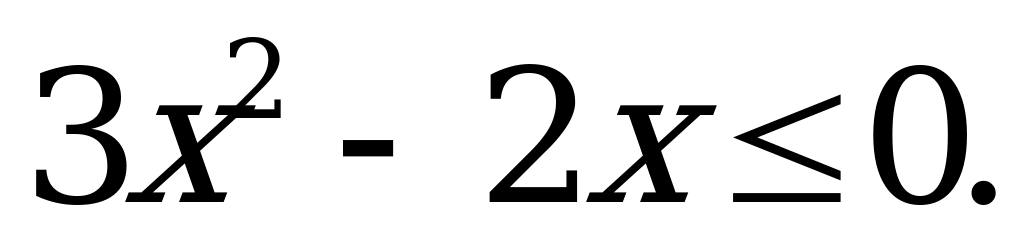 |
|
|
7 |
Решение неравенств методом интервалов | Решите неравенство методом интервалов: а)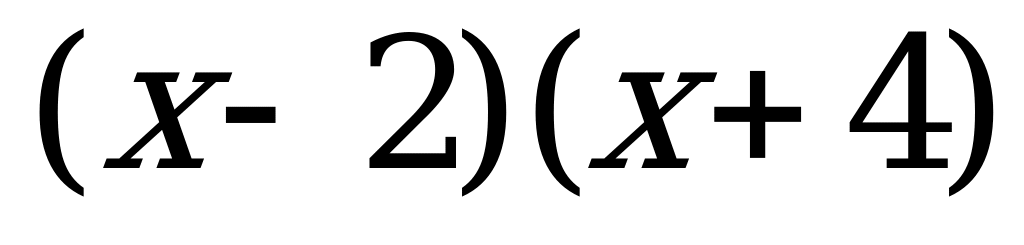 0; б) 0; б) 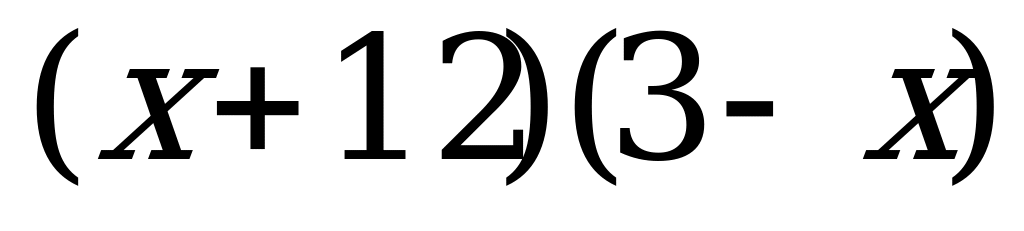 в) 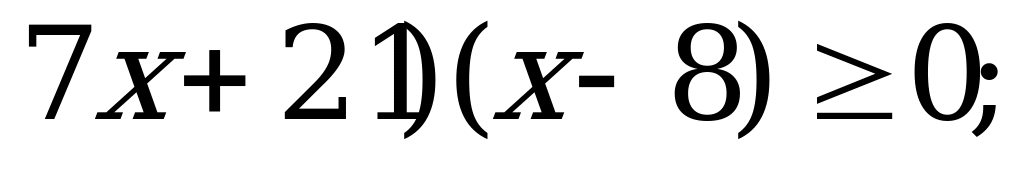 г) г) 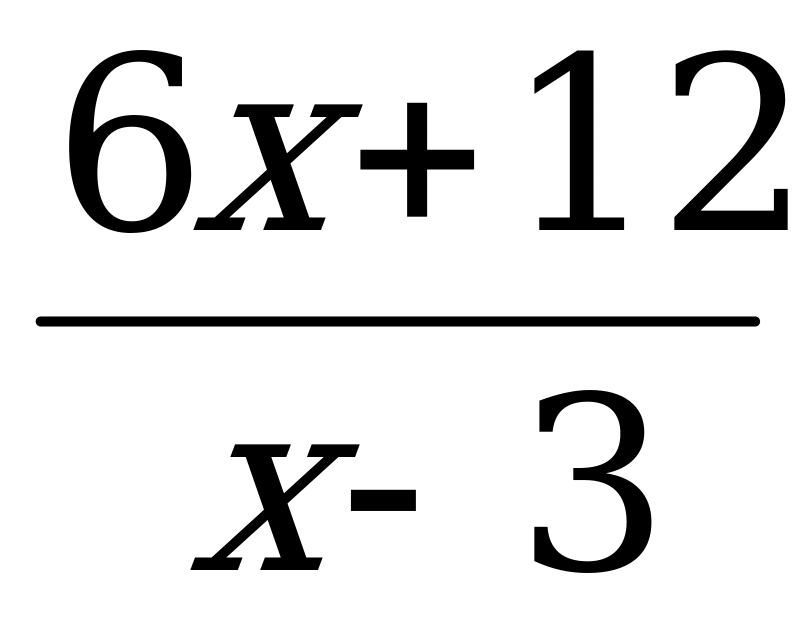 |
|
| 8 | Целое уравнение и его корни | Решите уравнение: а)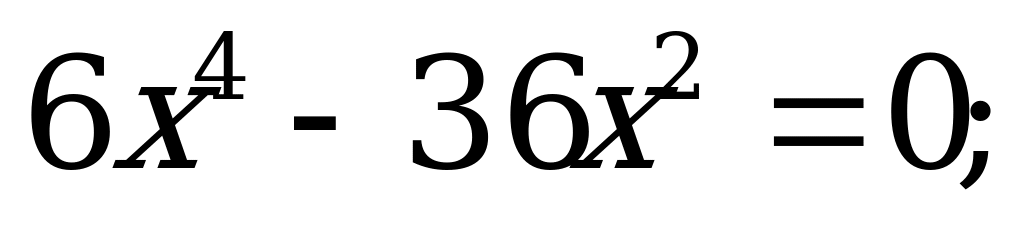 б) б)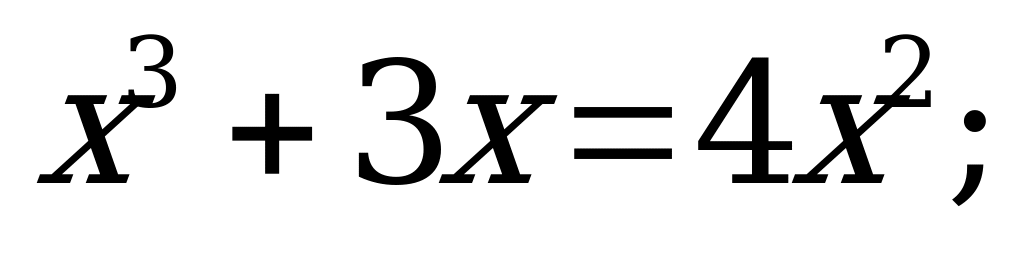 в) в)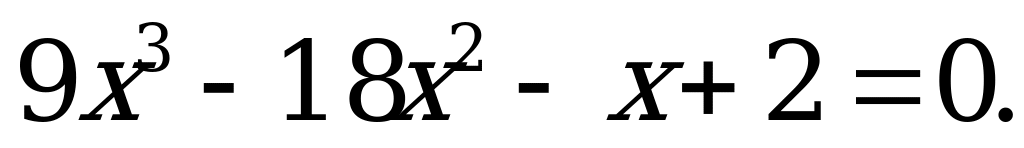 |
|
| 9 | Уравнения, приводимые к квадратным | Решите уравнение: а)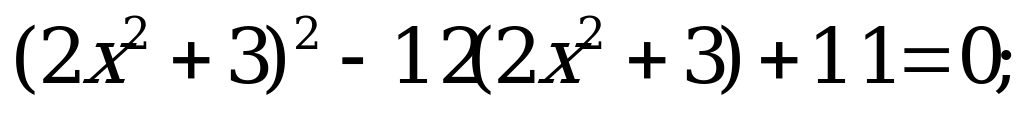 б) б)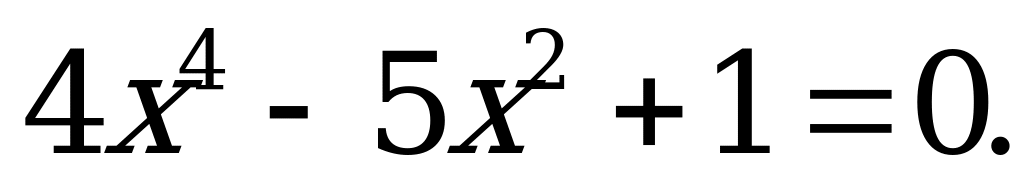 |
|
|
10 |
Решение систем уравнений второй степени с двумя неизвестными | Решите систему уравнений: а  ) х + у = 8, б) х² – у² = 16, ) х + у = 8, б) х² – у² = 16, х у = -20; х – у =2. |
|
| 11 | Решение задач с помощью систем уравнений второй степени | Диагональ прямоугольника равна 10см, а его периметр равен 28см. Найди стороны прямоугольника.
|
|
|
12 |
Определение арифметической прогрессии. Формула n – го члена арифметической прогрессии | 1). Найдите десятый член арифметической прогрессии: 6; 8;... 2). Найдите первый член арифметической прогрессии, если 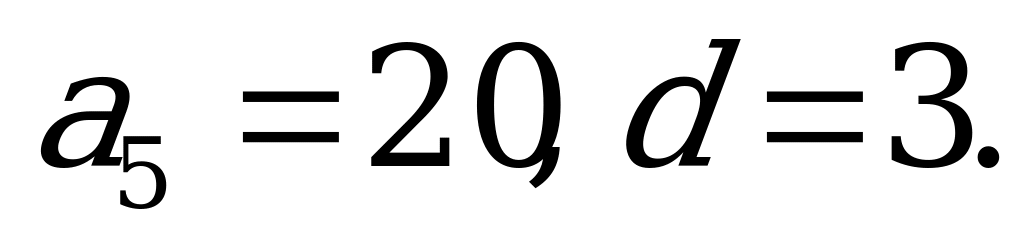
3). Найдите разность арифметической прогрессии, если 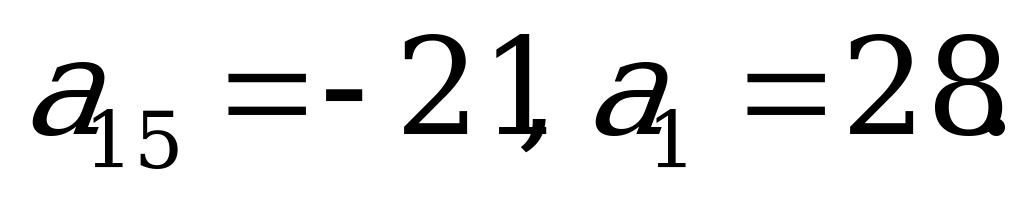
|
|
| 13 | Формула суммы n – первых членов арифметической прогрессии | Вычислите сумму девяти первых членов арифметической прогрессии, если 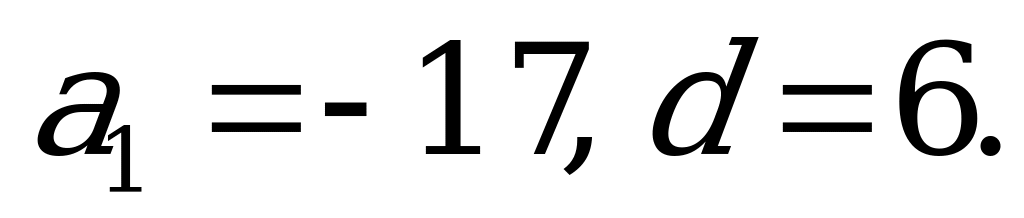
|
|
| 14 | Определение геометрической прогрессии. Формула n – го члена геометрической прогрессии | 1). Найдите седьмой член геометрической прогрессии: 2; -6;... 2). Найдите первый член геометрической прогрессии, если 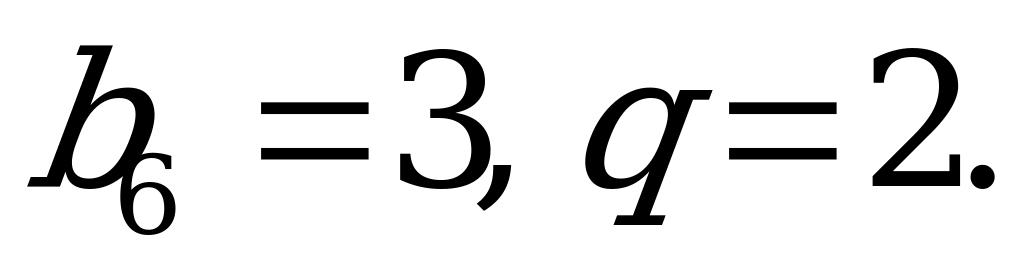
3). Найдите знаменатель геометрической прогрессии, если 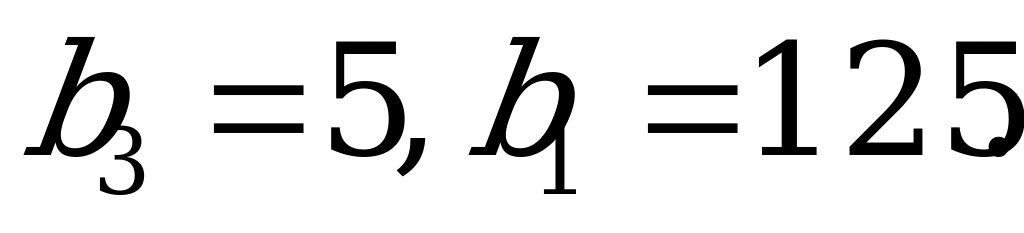
|
|
| № | Содержание материала | Практические задания |
|
| 15 | Формула суммы n – первых членов геометрической прогрессии | Вычислите сумму пяти первых членов геометрической прогрессии, если 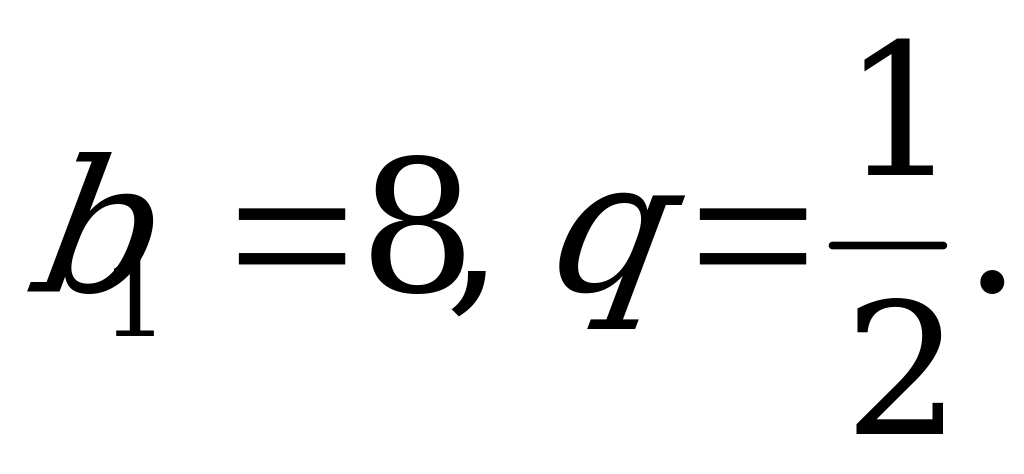 |
|
| 16 | Сумма бесконечной геометрической прогрессии при q | Найдите сумму бесконечной геометрической прогрессии: 9; 3; 1;... |
|
|
17 |
Четные и нечетные функции | Является ли четной или нечетной функция: а) 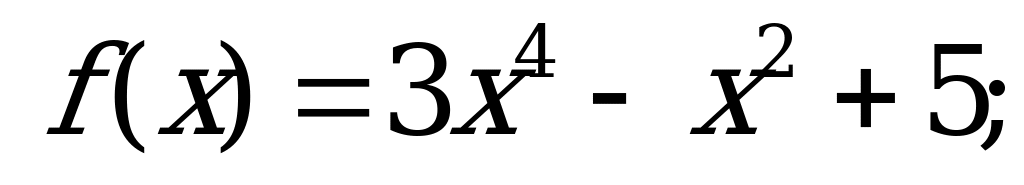 б) б) 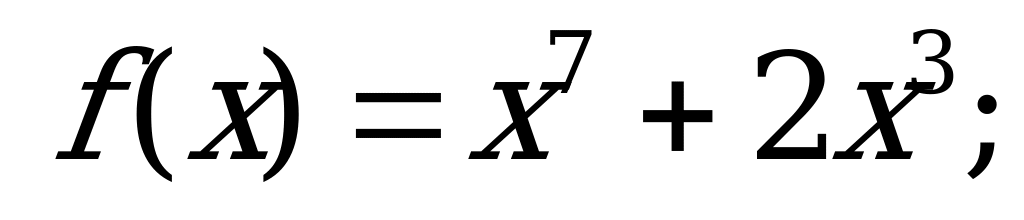 в) 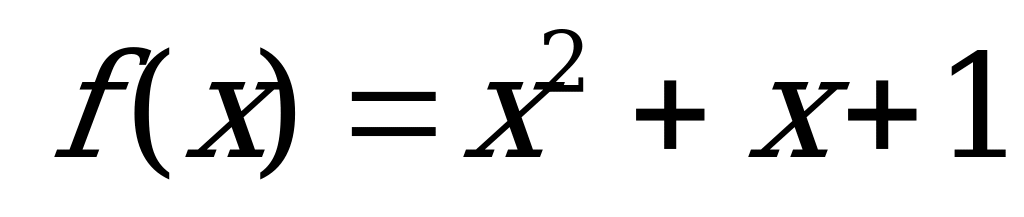 ? ? |
|
|
18 |
Определение корня п -степени его свойства. | 1).Вычислите: а) 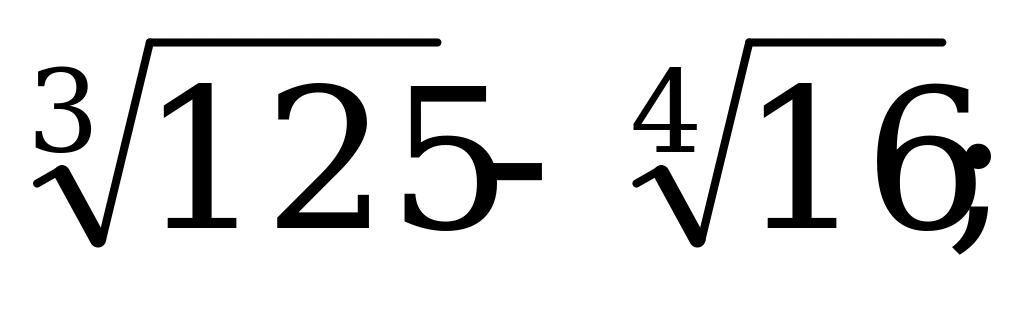 б) б) 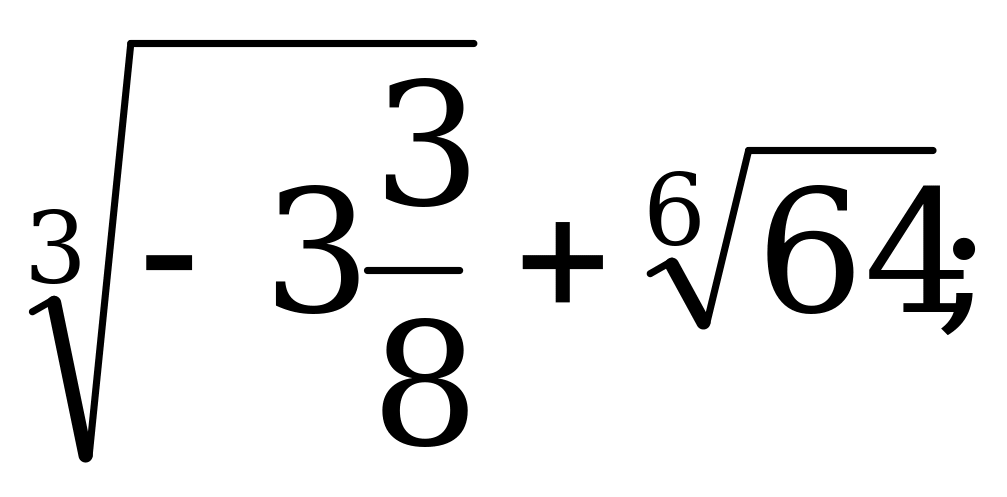 в) в) 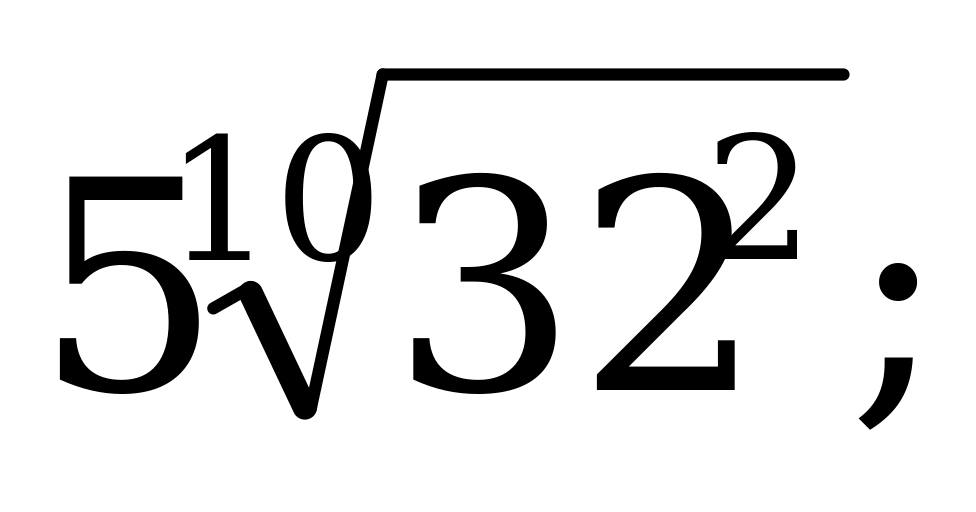 г) г) 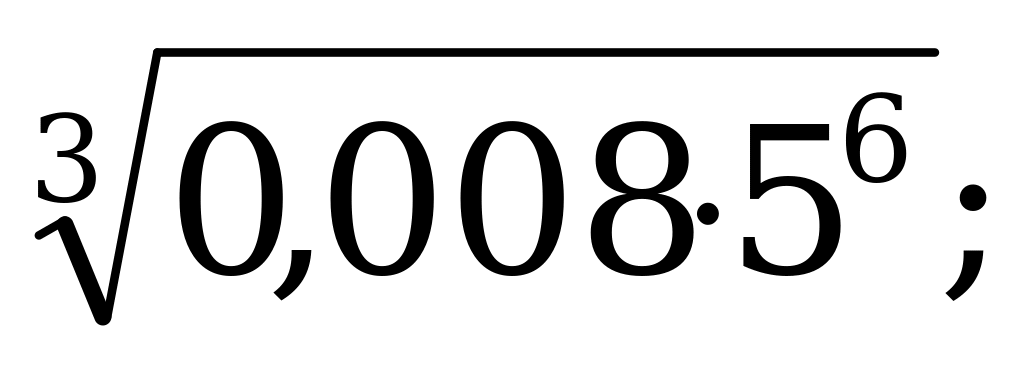 д) д) 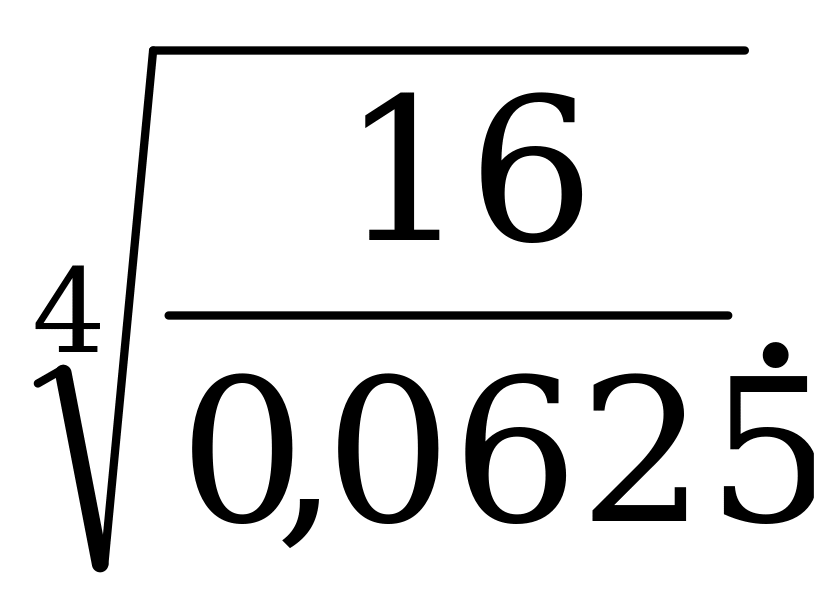 2). Решите уравнение: а)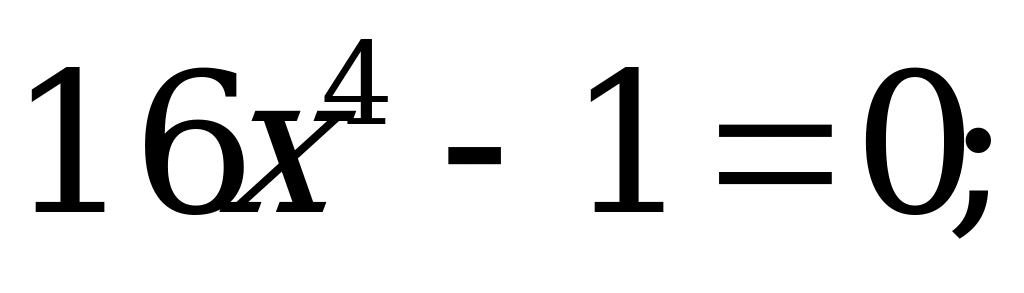 б) б)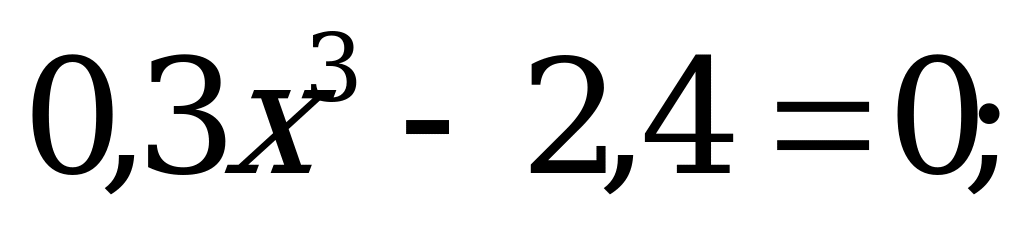 в) в)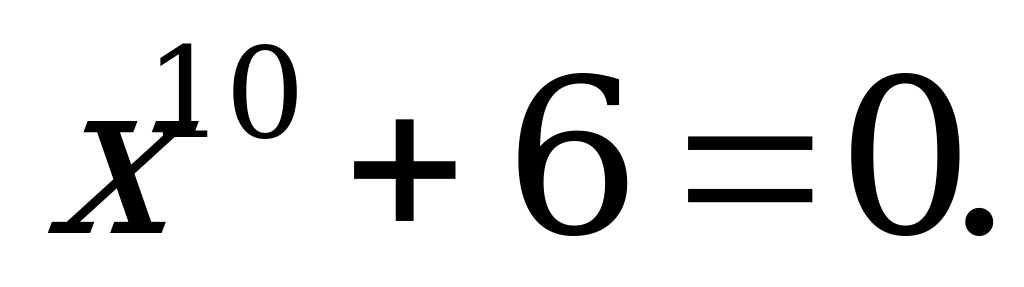 |
|
| 19 | Определение степени с дробным показателем и ее свойства | Найдите значение выражения: а) 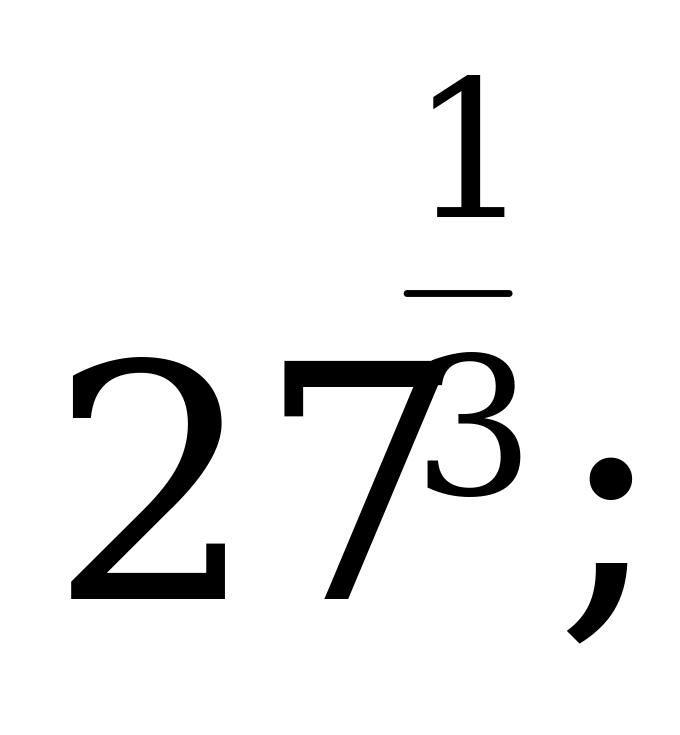 б) б) 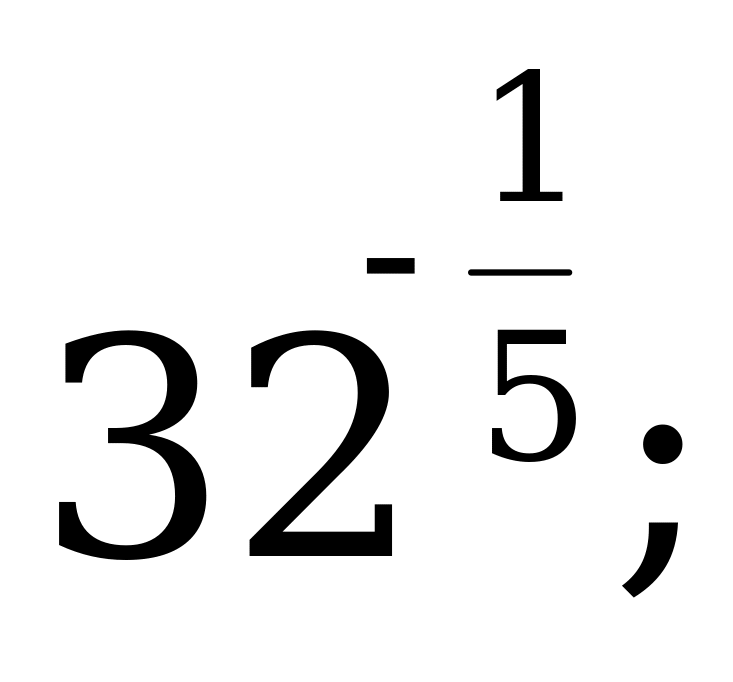 в) в) 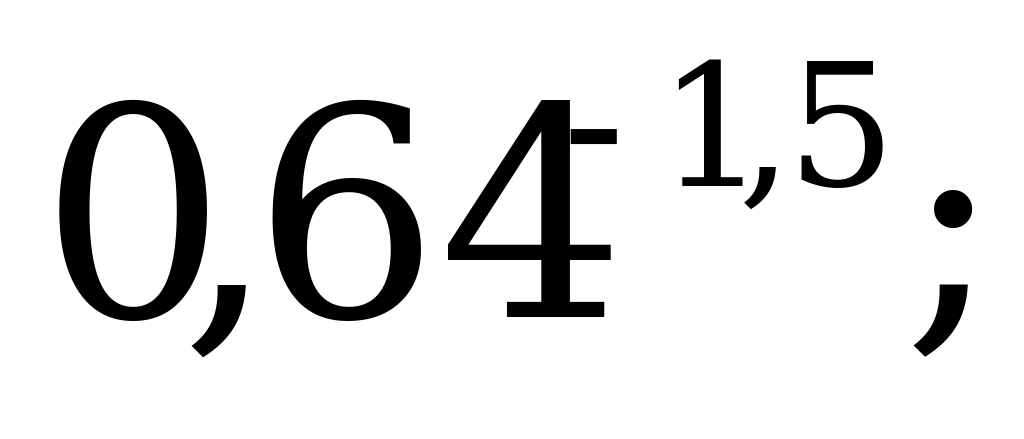 г) г) 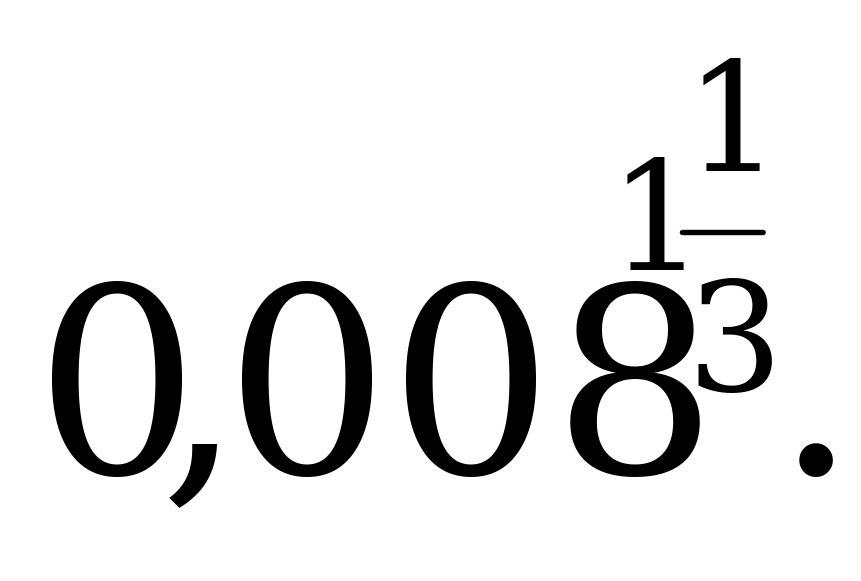 |
|
| 20 | Определение синуса, косинуса, тангенса и котангенса. Радианная мера угла | Вычислите: а) 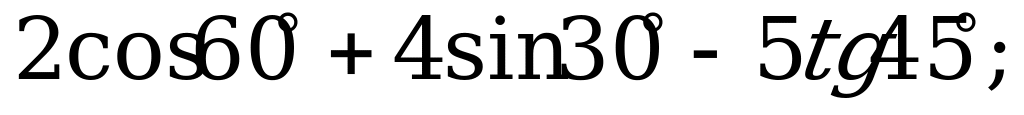 б) б) 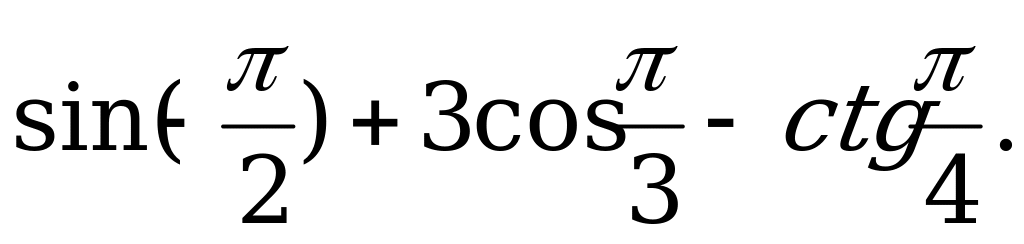
|
|
| 21 | Свойства синуса, косинуса, тангенса и котангенса | 1). Выясните, какой знак имеет: а) 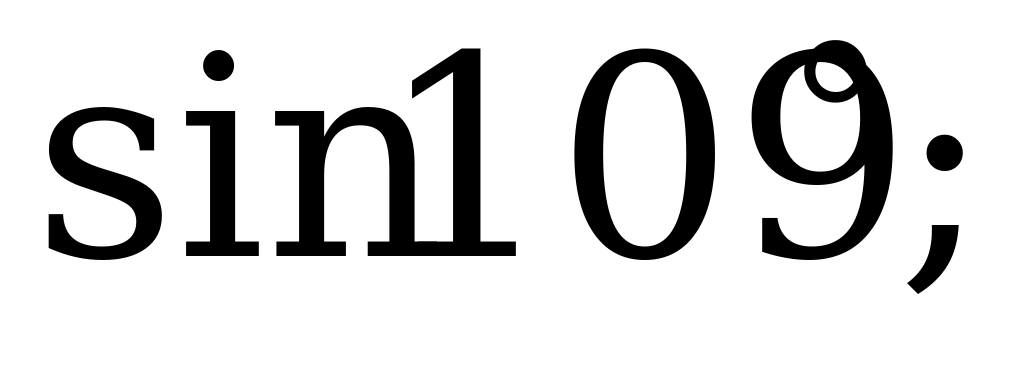 б) б)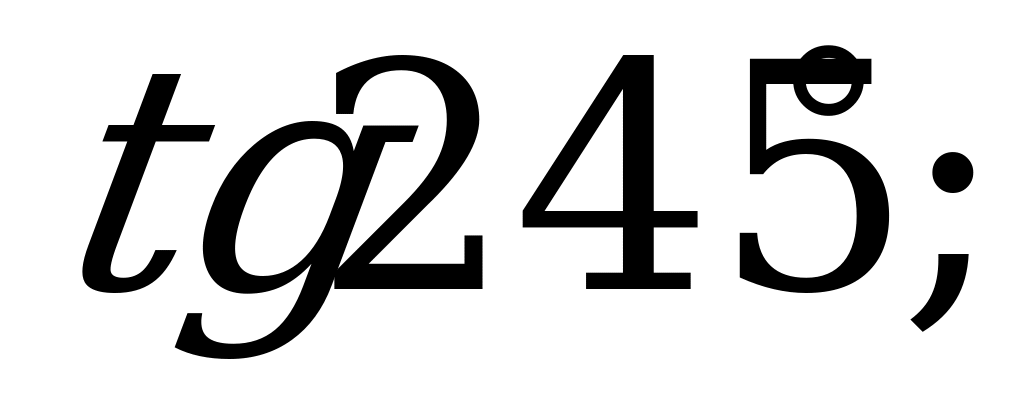 в) в)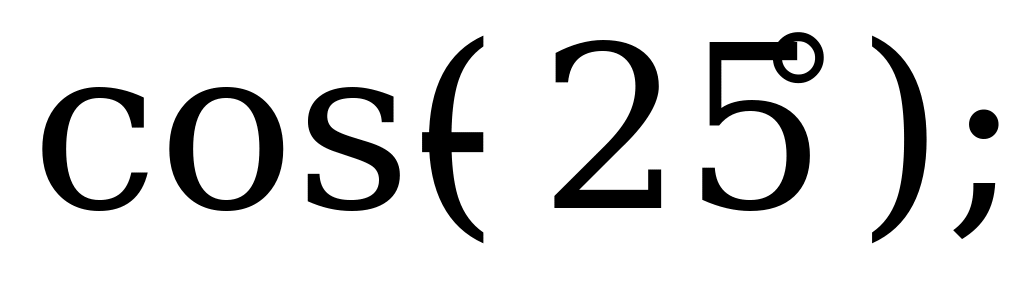 г) г)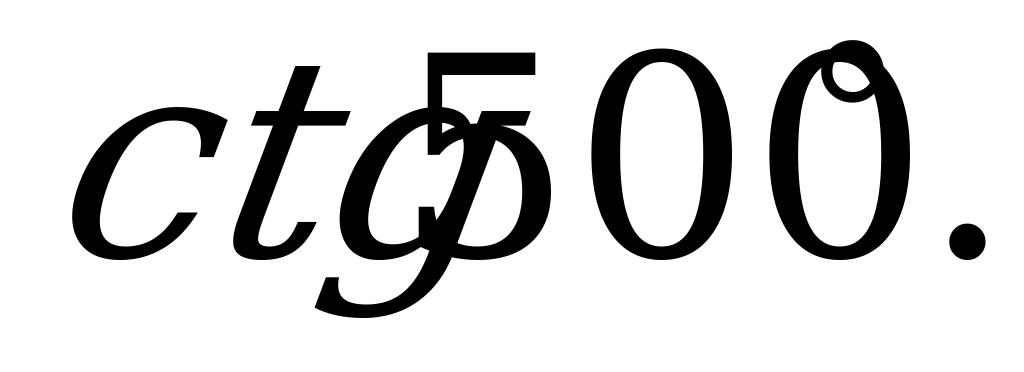 2). Вычислите: а) 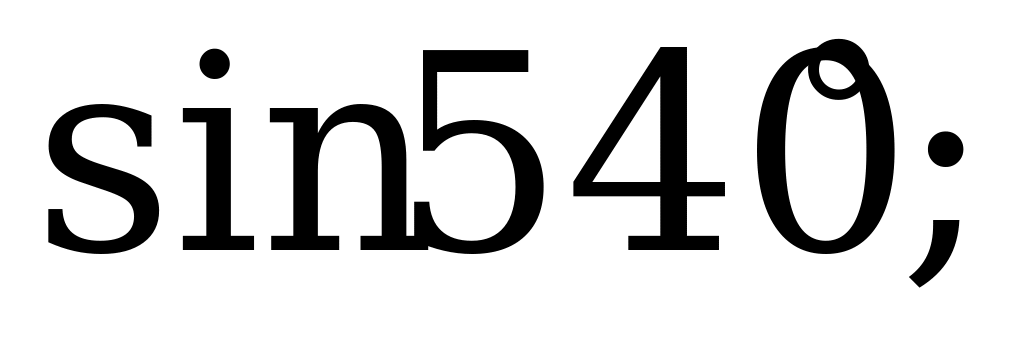 б) б)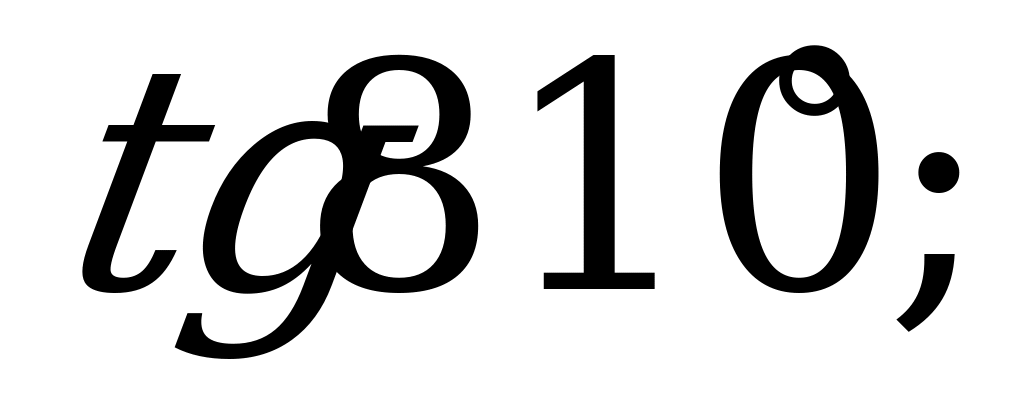 в) в)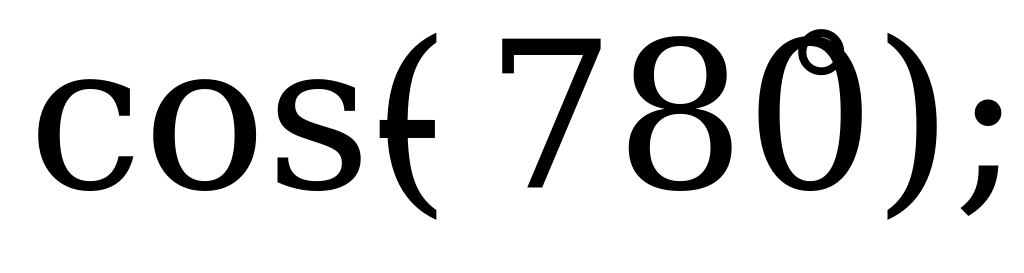 г) г)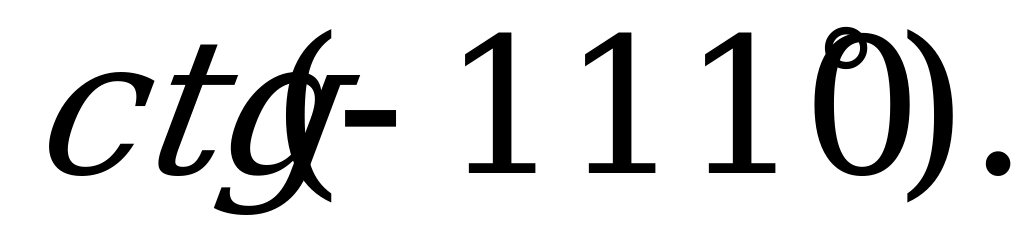
|
|
| 22 | Соотношения между тригонометрическими функциями одного и того же угла | Упростите выражение: а) 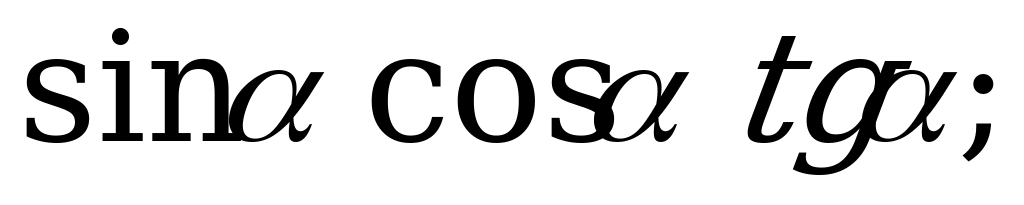 б) б) 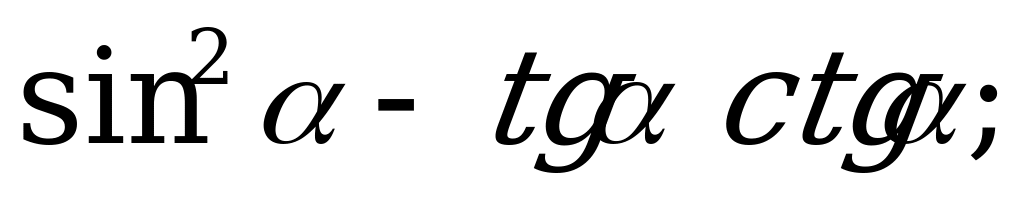 в) в) 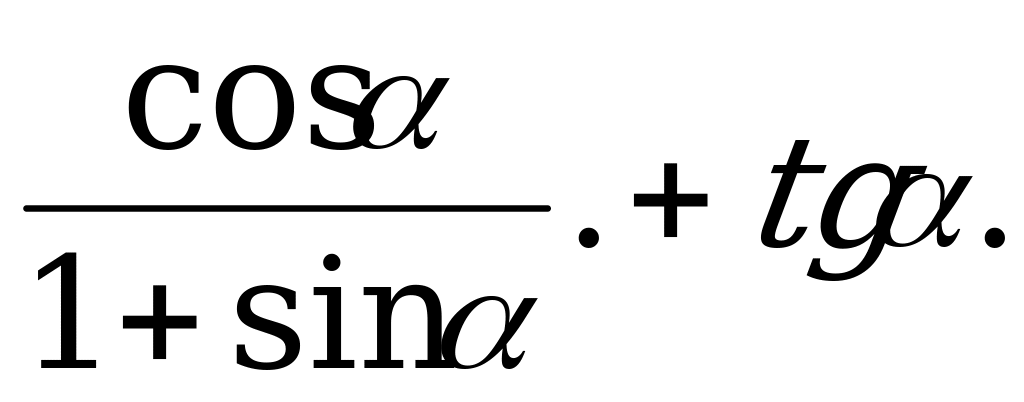
|
|
| № | Содержание материала | Практические задания |
|
|
23 |
Формулы приведения | Упростите выражение: а) 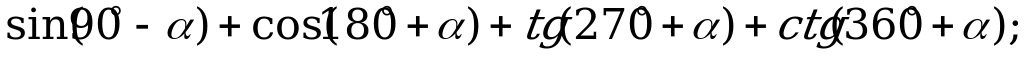 б) б) 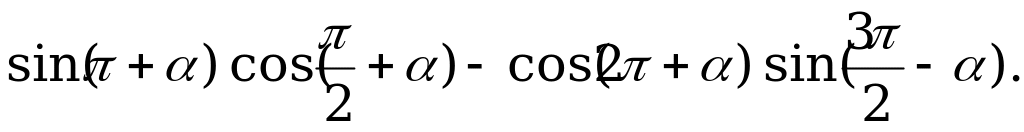 |
|
|
24 |
Формулы сложения | 1) Вычислите: а)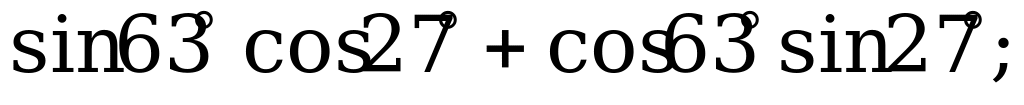 б) 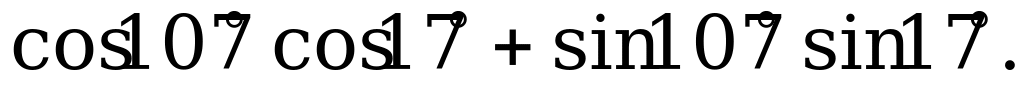 2). Упростите: 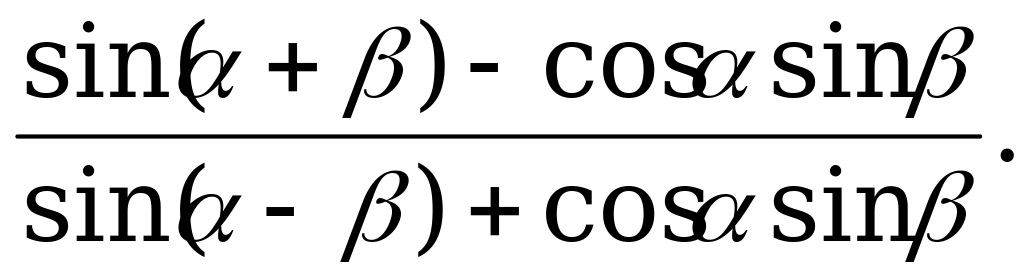
|
|
|
25 |
Формулы двойного угла | 1). Упростите выражение: а) 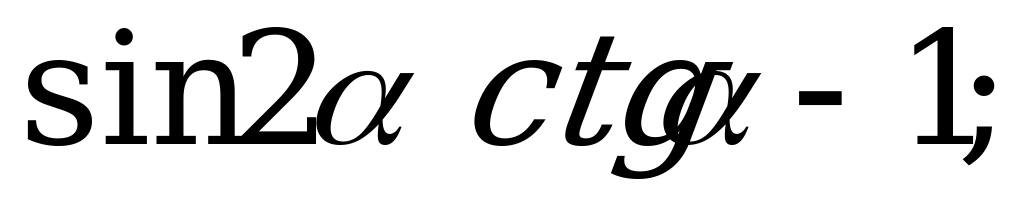 б) б)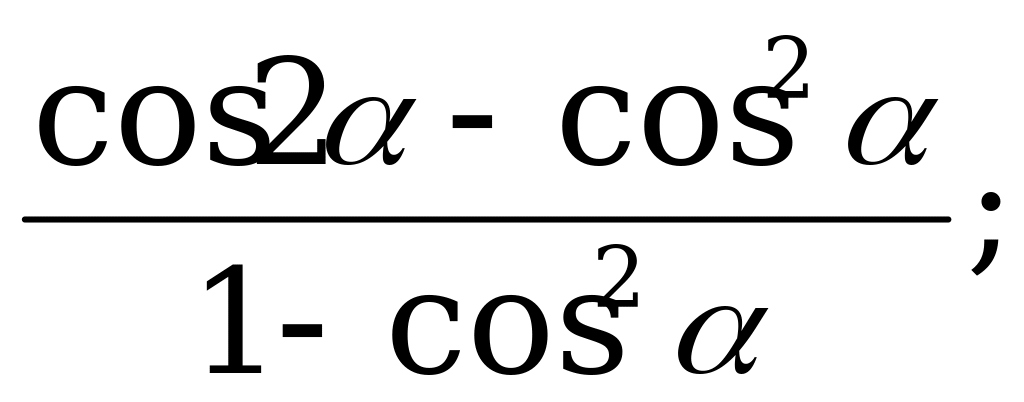 в) в) 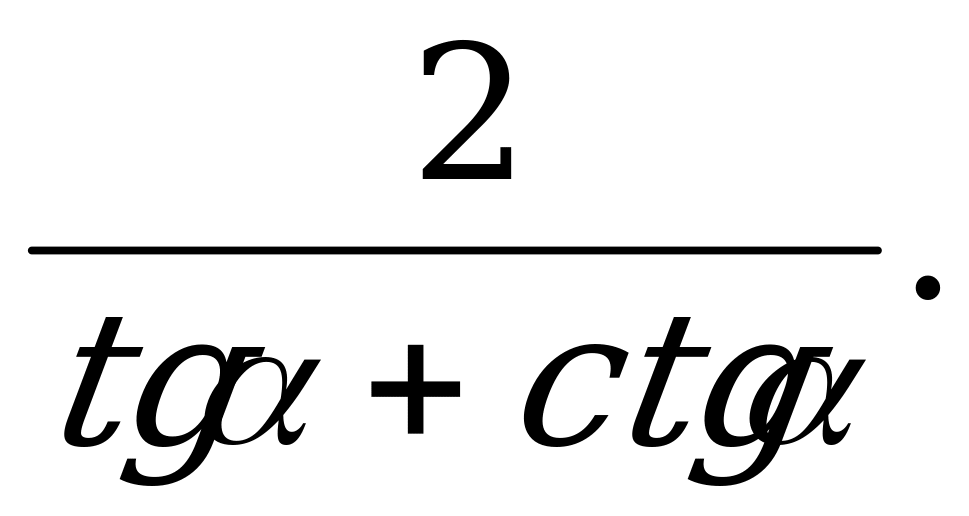 2) Вычислите: а) 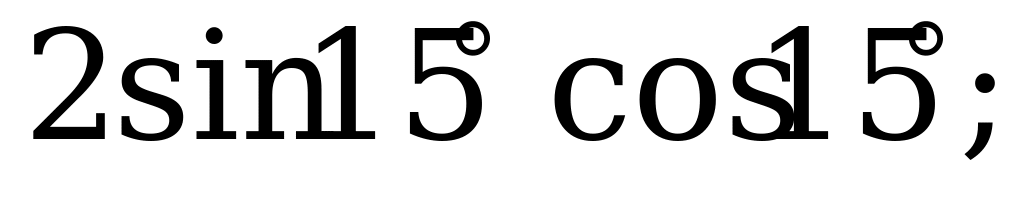 б) б)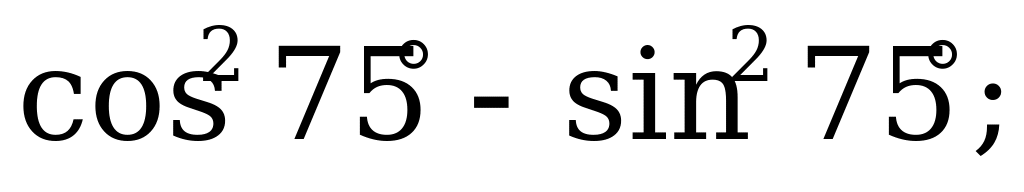 в) в) 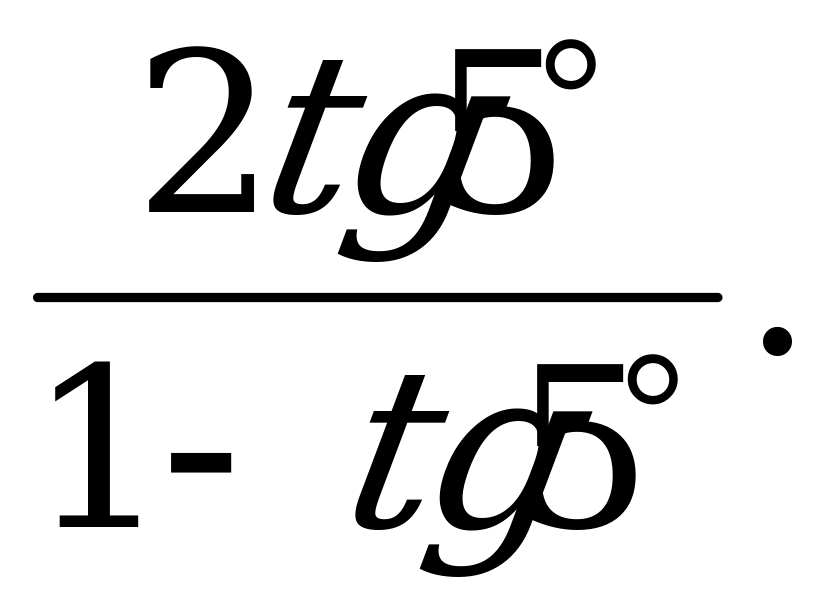 |
|
|
26 |
Формулы суммы и разности тригонометрических функций | 1). Упростите выражение: а) 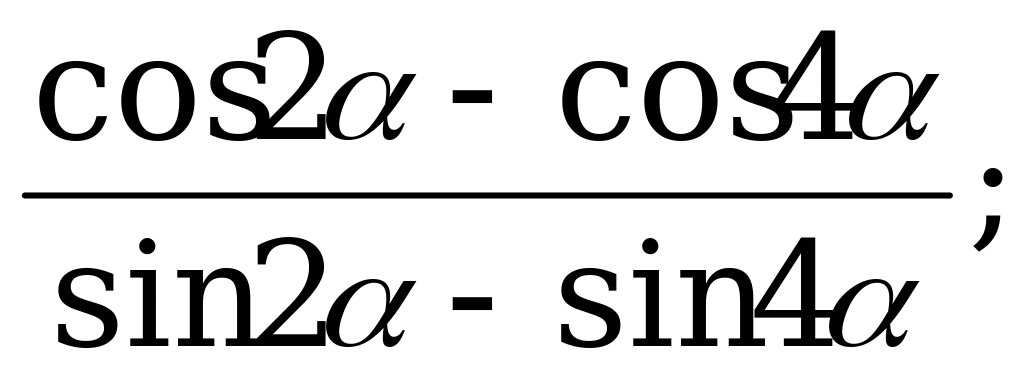 б) б) 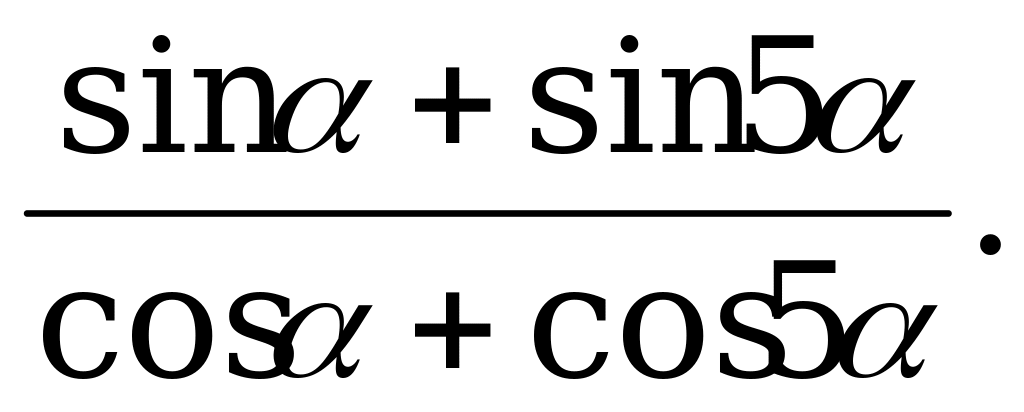 2). Найдите значение выражения: а) 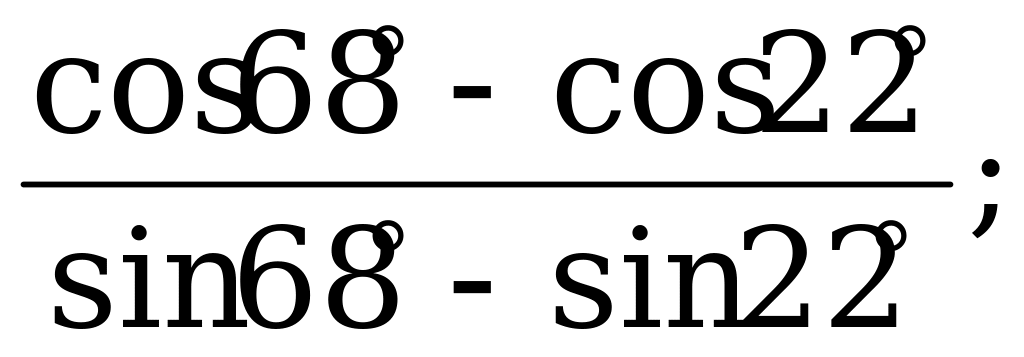 б) б) 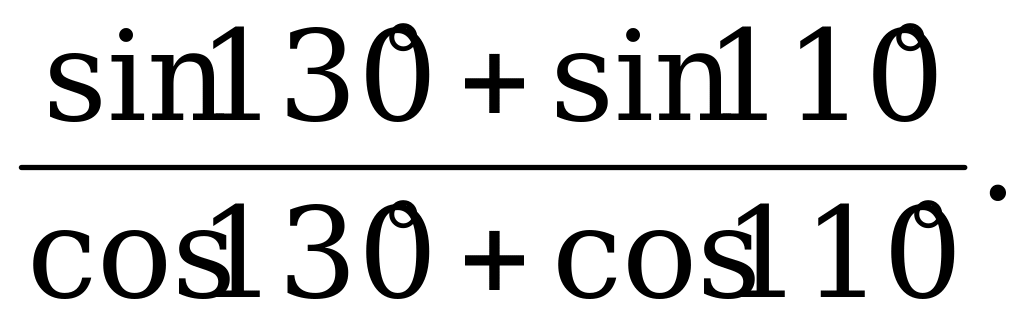 |
|