Вариант 3
1. Задание Запишите номера верных равенств.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
2. Задание Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
| Номер поезда | Отправление из Москвы | Прибытие в Санкт-Петербург |
| 038А | 00:43 | 08:45 |
| 020У | 00:53 | 09:02 |
| 016А | 01:00 | 08:38 |
| 116С | 01:00 | 09:06 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Петрову.
В ответе укажите номер правильного варианта.
1) 038А 2) 020У 3) 016А 4) 116С
3. Задание На координатной прямой изображены числа  и
и  . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?
В ответе укажите номер правильного варианта.

1)  2)
2)  3)
3)  4)
4) 
4. Задание Какое из данных ниже выражений при любых значениях  равно степени
равно степени  ?
?
1)  2)
2)  3)
3)  4)
4) 
5. Задание
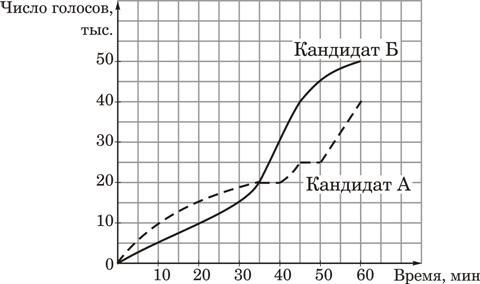 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
6. Задание Решите уравнение 
7. Задание Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
8.Задание
Вариант 3

На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какое из следующих утверждений неверно?
1) По площади территории Австралия занимает шестое место в мире.
2) Площадь территории Бразилии составляет 7,7 млн км2.
3) Площадь Индии меньше площади Китая.
4) Площадь Канады меньше площади России на 7,1 млн км2.
В ответе запишите номер выбранного утверждения.
9. Задание Какова вероятность того, что случайно выбранное натуральное число от 192 до 211 включительно делится на 5?
10. Задание На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках и
пересекает график в точках и
11. Задание Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
12. Задание Найдите значение выражения при
13 Задание.Закон всемирного тяготения можно записать в виде где  — сила притяжения между телами (в ньютонах),
— сила притяжения между телами (в ньютонах),  и
и  — массы тел (в килограммах),
— массы тел (в килограммах),  — расстояние между центрами масс (в метрах), а
— расстояние между центрами масс (в метрах), а  — гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела
— гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела  (в килограммах), если Н, кг, а
(в килограммах), если Н, кг, а  м.
м.
14. Задание Укажите решение системы неравенств
15. Задание Какой угол (в градусах) описывает минутная стрелка за 10 мин?
16. Задание Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
В ответе запишите величины различных углов в порядке возрастания без пробелов.
Вариант 3
17. Задание
В угол C величиной 57° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.
18. Задание
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 97. Найдите площадь четырёхугольника ABMN.
19. Задание
Найдите тангенс угла AOB.
20. Задание Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
21. Задание Решите систему неравенств
22. Задание Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
23. Задание Постройте график функции и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
24. Задание В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
25. Задание Окружности с центрами в точках  и
и  не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
26. Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Вариант 4
1. Задание Найдите значение выражения
2. Задание В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах.
| Магазин | Консервированый горошек (за банку) | Домашний творог (за кг) | Сыр (за кг) |
| «Караван» | 36 | 1000 | 256 |
| «Народный» | 30 | 930 | 258 |
| «Камея» | 32 | 950 | 260 |
Лидия Михайловна хочет купить 3 банки консервированного горошка, 1 кг домашнего творога и 0,5 кг сыра. В каком магазине стоимость такой покупки будет наименьшей, если в «Камее» у Лидии Михайловны скидка 8% на любые молочные продукты, а в «Караване» скидка 2% на весь ассортимент?
1) в «Караване» 2) в «Народном» 3) в «Камее» 4) во всех магазинах стоимость покупки будет одинаковой
3. Задание На координатной прямой отмечены числа a, b, и c.
В ответе укажите номер правильного варианта.

Укажите номер верного утверждения.
1) 2) 3) 4)
4. Задание Найдите значение выражения
1) 2) 3) 4)
3) 4)
5. Задание На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник.
6. Задание Решите уравнение Если корней больше одного, в ответе укажите бóльший корень.
7. Задание Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Пакет сока стоит в магазине 75 рублей, а пенсионер заплатил за него 61 рубль 50 копеек. Сколько процентов составляет скидка для пенсионера?
8. Задание
На диаграмме показано содержание питательных веществ в молочном шоколаде. Определите по диаграмме, содержание каких веществ превосходит 50%.
*-к прочему относятся вода, витамины и минеральные вещества.
1) жиры 2) белки 3) углеводы 4) прочее
9. Задание На экзамене по биологии школьнику достаётся один случайно выбранный вопрос из списка. Вероятность того, что этот вопрос на тему «Членистоногие», равна 0,15. Вероятность того, что это окажется вопрос на тему «Ботаника», равна 0,45. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Вариант 4
10. Задание
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Наибольшее значение функции равно 9
2) Функция убывает на промежутке ( −∞; 2 ]
3) f(x)x
11. Задание Выписано несколько последовательных членов геометрической прогрессии: … ; 150 ; x ; 6 ; 1,2 ; … Найдите член прогрессии, обозначенный буквой x.
12. Задание Найдите значение выражения при
13. Задание Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 27 Дж, I = 1,5 A, R = 2 Ом.
14. Задание На каком рисунке изображено множество решений неравенства ?
15 Задание.Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
16. Задание
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 38°, угол CADравен 54°. Найдите угол ABC. Ответ дайте в градусах.
17. Задание
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 9 , AO = 15 .
Вариант 4
18. Задание
На стороне BC прямоугольника ABCD, у которого AB = 5 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
19. Задание
На рисунке изображен параллелограмм  . Используя рисунок, найдите .
. Используя рисунок, найдите .
20. Задание Какие из следующих утверждений верны?
1) Две прямые, перпендикулярные третьей прямой, перпендикулярны.
2) В любой прямоугольной трапеции есть два равных угла.
3) Все диаметры окружности равны между собой.
21. Задание Найдите значение выражения если
22. Задание Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 100 км. Отдохнув, он отправился обратно в А, увеличив скорость на 15 км/ч. По пути он сделал остановку на 6 часов, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
23. Задание Парабола проходит через точки A(0; 4), B(1; 11), C(–5; –1). Найдите координаты её вершины.
24. Задание Точка H является основанием высоты BH, проведённой из вершины прямого угла Bпрямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 15.
25. Задание Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что отрезки AB и IJ перпендикулярны.
26. Задание Окружности радиусов 60 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.






 На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?
На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего телезрителей проголосовало к 40-й минуте дебатов?











