|
| Мальчики | Девочки |
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Количество раз | 58 | 56 | 54 | 66 | 64 | 62 |
2 вариант 1. Задание 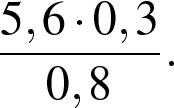
Найдите значение выражения
2. Задание 2 № 316601
В таблице приведены нормативы по прыжкам через скакалку за 30 сек. для 9 класса.
Какую оценку получит мальчик, прыгнувший 57 раз за 30 сек.?
В ответе укажите номер правильного варианта.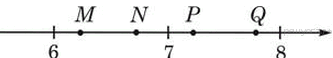
1) «5» 2) «4» 3) «3» 4) «Неудовлетворительно»
3. Задание
Одна из точек, отмеченных на координатной прямой, соответствует числу  Какая это точка?
Какая это точка?
1) точка M 2) точка N 3) точка P 4) точка Q
4. Задание
Найдите значение выражения 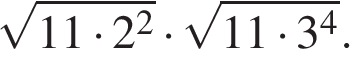 В ответе укажите номер правильного варианта.
В ответе укажите номер правильного варианта.
1) 198 2) 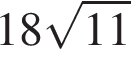 3) 3564 4) 2178
3) 3564 4) 2178
5. Задание
В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
| Вещество | Дети от 1 года до 14 лет | Мужчины | Женщины |
| Жиры | 40—97 | 70—154 | 60—102 |
| Белки | 36—87 | 65—117 | 58—87 |
| Углеводы | 170—420 | 257—586 |
Какой вывод о суточном потреблении жиров, белков и углеводов 7-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
6. Задание
Найдите корни уравнения 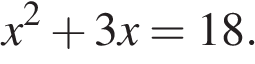
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
7. Задание
После уценки телевизора его новая цена составила 0,52 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?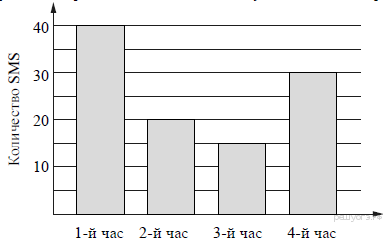
8. Задание
На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.
9. Задание
Из 1500 карт памяти, поступивших в продажу, в среднем 30 не работают. Какова вероятность того, что случайно выбранная в магазине карта работает?
10. Задание
На рисунке изображён график функции 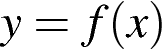 . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.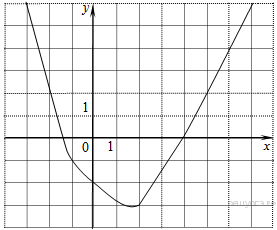
1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в
пересекает график в
точках 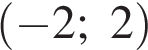 и
и 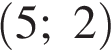
11. Задание 11
Дана арифметическая прогрессия (аn): −6; −2; 2; 6; 10… . Найдите a8.
12. Задание 12
Упростите выражение 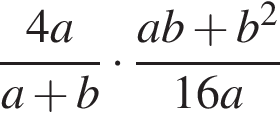 и найдите его значение при
и найдите его значение при 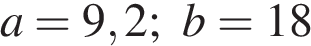 . В ответе запишите найденное значение.
. В ответе запишите найденное значение.
13. Задание
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n=1800 ? Ответ выразите в километрах.
14. Задание 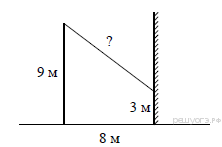
Укажите решение неравенства 
1)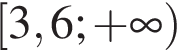 2)
2)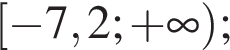 3)
3)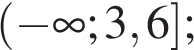 4)
4)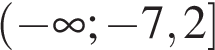
15. Задание
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
16. Задание 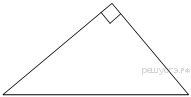
В прямоугольном треугольнике катет и гипотенуза равны 20 и 25 соответственно. Найдите другой катет этого треугольника.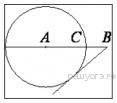
17. Задание
На отрезке  выбрана точка
выбрана точка  так, что и . Построена окружность с центром
так, что и . Построена окружность с центром  , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки  к этой окружности.
к этой окружности.
18. Задание
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
19. Задание
Найдите тангенс угла  треугольника
треугольника  , изображённого на рисунке.
, изображённого на рисунке.
20. Задание
Какие из следующих утверждений верны?
1. Один из углов треугольника всегда не превышает 60 градусов.
2. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3. Две прямые, параллельные третьей прямой, перпендикулярны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
| № п/п | Ответ |
| 1 | 2,1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 1 |
| 5 | 13|31 |
| 6 | -63 |
| 7 | 48 |
| 8 | 15 |
| 9 | 0,98 |
| 10 | 12 |
| 11 | 22 |
| 12 | 4,5 |
| 13 | 1,44 |
| 14 | 1 |
| 15 | 10 |
| 16 | 15 |
| 17 | 51 |
| 18 | 12 |
| 19 | 0,4 |
| 20 | 12|21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|































