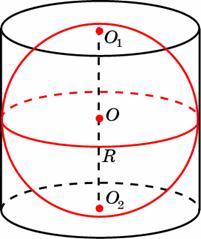
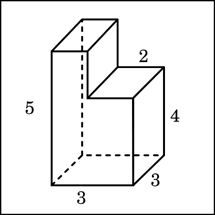
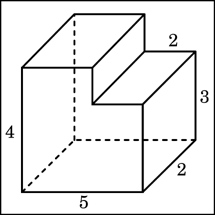
| Вариант I. 1.Радиус основания цилиндра равен 9,5, высота равна 4. Найдите площадь боковой поверхности цилиндра, деленную на 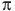 . . 2. Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса. 3. Шар вписан в цилиндр. Объем шара равен 24. Найдите объем цилиндра. 4. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые). 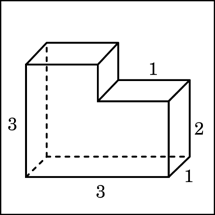
5. В сосуд, имеющий форму правильной треугольной призмы, налили 2300  воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в  . . 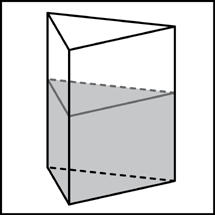
6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке O. Площадь треугольника ABC равна 16, объем пирамиды равен 80. Найдите длину отрезка SС. 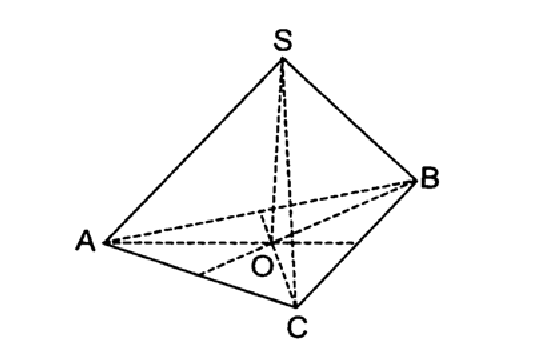
| Вариант II. 1. Высота конуса равна 24, а длина образующей — 25. Найдите диаметр основания конуса. 2. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра. 3. Шар вписан в цилиндр. Объем цилиндра равна 6. Найдите объем шара. 4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. 5. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.
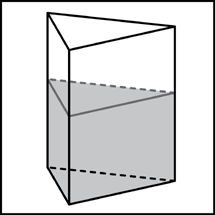
6. Во сколько раз объём конуса, описанного около правильной четырёхугольной пирамиды, больше объёма конуса, вписанного в эту пирамиду? 
|