Призма
| 1. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 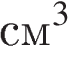 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ: 184 |
 |
| 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ: 5 |
| 3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10. Ответ: 300
| 
|
| 4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. Ответ: 248
| 
|
| 5. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. Ответ: 12
| 
|
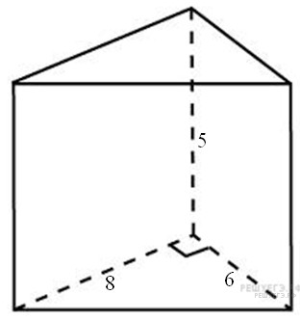
| 6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы. Ответ: 120
| 
|
| 7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60 . Одно из ребер параллелепипеда составляет с этой гранью угол в 60 . Одно из ребер параллелепипеда составляет с этой гранью угол в 60 и равно 2. Найдите объем параллелепипеда. и равно 2. Найдите объем параллелепипеда. Ответ: 1,5 | 
|
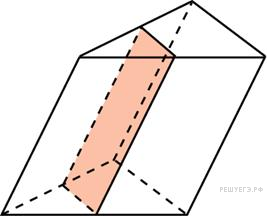
| 8. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы. Ответ: 8 |
|
| 9. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5. Ответ: 20 |
| 10. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. Ответ: 4 |
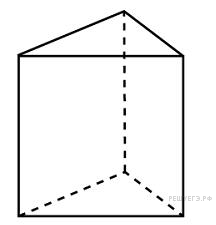
| 11. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности. Ответ: 288
| 
|
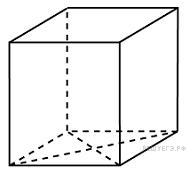
| 12. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы. Ответ: 10
| 
|
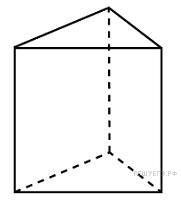
| 13. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. Ответ: 10
| 
|
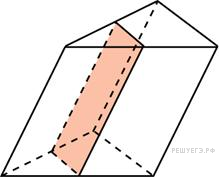
| 14. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы. Ответ: 16
| 
|
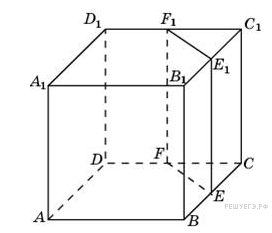
| 15. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины. Ответ: 1,5
| 
|
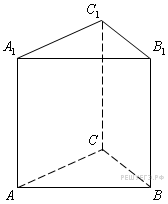
| 16. Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3. Ответ: 2 |
| 17. Найдите объем многогранника, вершинами которого являются точки 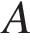 , , 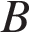 , , 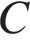 , ,  , ,  правильной треугольной призмы правильной треугольной призмы 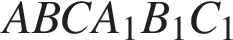 , площадь основания которой равна 3, а боковое ребро равно 2. , площадь основания которой равна 3, а боковое ребро равно 2. Ответ: 4
| 
|
| 18. Найдите объем многогранника, вершинами которого являются точки  , , 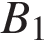 , , 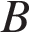 , , 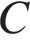 правильной треугольной призмы правильной треугольной призмы 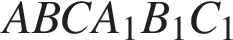 , площадь основания которой равна 4, а боковое ребро равно 3. , площадь основания которой равна 4, а боковое ребро равно 3. Ответ: 4
|
| 19. Найдите объем многогранника, вершинами которого являются точки 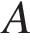 , , 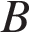 , , 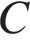 , ,  , ,  , ,  , ,  правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3. правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3. Ответ: 4 |
| 20. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3. Ответ: 3 |
| 21. Найдите объем многогранника, вершинами которого являются точки 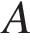 , , 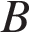 , ,  , ,  , ,  , , 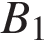 , ,  , ,  правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2. правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2. Ответ: 8
| |
| 22. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2. Ответ: 6
| |
| 23. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней? Ответ: 54 |
| 24. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3. Ответ: 50
| |
| 25. Найдите расстояние между вершинами А и D прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA = 3. = 3. Ответ: 5
| |
| 26. В правильной шестиугольной призме все ребра равны 1. Найдите расстояние между точками 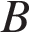 и и  . . Ответ: 2
| |
| 27. В правильной шестиугольной призме все ребра равны 1. Найдите угол Ответ дайте в градусах. Ответ: 60
| |
| 28. В правильной шестиугольной призме , все ребра которой равны 8, найдите угол между прямыми  и и  . Ответ дайте в градусах. . Ответ дайте в градусах. Ответ: 60 |
| 29. В кубе найдите угол между прямыми  и и  . Ответ дайте в градусах. . Ответ дайте в градусах. Ответ: 60 |
| 30. В правильной треугольной призме 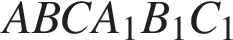 , все ребра которой равны 3, найдите угол между прямыми , все ребра которой равны 3, найдите угол между прямыми  и и  . Ответ дайте в градусах. . Ответ дайте в градусах. Ответ: 45 |
| 31. В правильной четырёхугольной призме известно, что . Найдите угол между диагоналями  и и  . Ответ дайте в градусах. . Ответ дайте в градусах. Ответ: 60 |
| 32. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1. Ответ: 5
| |
| 33. В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1 равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C. Ответ: 120
| |
| 34. Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 2. Найдите объём куба. Ответ: 16
| |
| 35. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 9, AD = 12 , AA1 = 18. Найдите синус угла между прямыми A1D1 и AC. Ответ: 0,6
| |
| 36. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 5, найдите угол между прямыми FA и D1E1. Ответ дайте в градусах. Ответ: 60
| |
| 37. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. Ответ: 4
| |
| 38. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны  . . Ответ: 4,5 |

|
| 39.Найдите объем правильной шестиугольной призмы, все ребра которой равны  . . Ответ: 13,5 |
| 40. В правильной шестиугольной призме все ребра равны 1. Найдите расстояние между точками 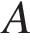 и и  . . Ответ: 2 |
| 41. В правильной шестиугольной призме все ребра равны  Найдите расстояние между точками Найдите расстояние между точками 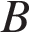 и и  Ответ: 5 |
| 42. В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла  Ответ: 2 |
| 43. В правильной шестиугольной призме все ребра равны 1. Найдите угол  . Ответ дайте в градусах. . Ответ дайте в градусах. Ответ: 60 |
| 44. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы. Ответ: 240 | |
| 45. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы. Ответ: 12 | |
| 46. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом 30 Ответ: 18 | |
Куб
1. Площадь поверхности куба равна 18. Найдите его диагональ. Ответ: 3
2. Объем куба равен 8. Найдите площадь его поверхности. Ответ: 24
3. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. Ответ: 4
4. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза? Ответ: 27
5. Диагональ куба равна  . Найдите его объем. Ответ: 8
. Найдите его объем. Ответ: 8
6. Объем куба равен . Найдите его диагональ. Ответ: 6
7. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. Ответ: 2
8. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза? Ответ: 9
9. Диагональ куба равна 1. Найдите площадь его поверхности. Ответ: 2
10. Площадь поверхности куба равна 24. Найдите его объем. Ответ: 8
11. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Ответ: 4
12. В кубе точка  — середина ребра
— середина ребра  , точка
, точка  — середина ребра
— середина ребра  , точка
, точка  — середина ребра
— середина ребра  . Найдите угол . Ответ дайте в градусах. Ответ: 60
. Найдите угол . Ответ дайте в градусах. Ответ: 60
Прямоугольный параллелепипед
1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Ответ: 5
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. Ответ: 3
3. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. Ответ: 24
4. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда. Ответ: 48
5. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру. Ответ: 8
6. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани. Ответ: 5
7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины. Ответ: 4
8. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. Ответ: 6
9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. Ответ: 32
10. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ. Ответ: 7
11. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна  и образует с плоскостью этой грани угол 45
и образует с плоскостью этой грани угол 45 . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
Ответ: 4
12. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности. Ответ: 22
13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Ответ: 64
14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности. Ответ: 22
15. Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды . Ответ: 1,5
16. Найдите объем многогранника, вершинами которого являются точки 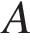 ,
,  ,
,  ,
, 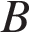 ,
,  ,
, 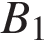 прямоугольного параллелепипеда , у которого ,
прямоугольного параллелепипеда , у которого ,  ,
,  . Ответ: 30
. Ответ: 30
17. Найдите объем многогранника, вершинами которого являются точки 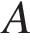 ,
, 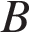 ,
,  ,
,  прямоугольного параллелепипеда , у которого
прямоугольного параллелепипеда , у которого  , ,
, ,  .
.
Ответ: 8
18.Найдите объем многогранника, вершинами которого являются точки  ,
, 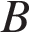 ,
, 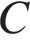 ,
,  ,
, 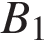 прямоугольного параллелепипеда , у которого
прямоугольного параллелепипеда , у которого  , ,
, ,  . Ответ: 16
. Ответ: 16
19. Найдите объем многогранника, вершинами которого являются точки 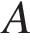 ,
, 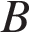 ,
, 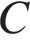 ,
, 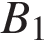 прямоугольного параллелепипеда , у которого , ,
прямоугольного параллелепипеда , у которого , ,  .
.
Ответ: 6
20. Найдите объем многогранника, вершинами которого являются точки 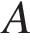 ,
, 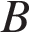 ,
, 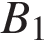 ,
,  прямоугольного параллелепипеда , у которого , ,
прямоугольного параллелепипеда , у которого , ,  .
.
Ответ: 10
21. Найдите угол прямоугольного параллелепипеда, для которого ,  ,
,  . Дайте ответ в градусах. Ответ: 45
. Дайте ответ в градусах. Ответ: 45
22. В прямоугольном параллелепипеде известно, что  = 4,
= 4,  = 3,
= 3,  = 5. Найдите угол DBD1. Ответ дайте в градусах. Ответ: 45
= 5. Найдите угол DBD1. Ответ дайте в градусах. Ответ: 45
23.В прямоугольном параллелепипеде известно, что , , . Найдите длину ребра  . Ответ: 1
. Ответ: 1
24. В прямоугольном параллелепипеде ребро , ребро , ребро  . Точка
. Точка  — середина ребра
— середина ребра  Найдите площадь сечения, проходящего через точки
Найдите площадь сечения, проходящего через точки 
 и
и  . Ответ: 5
. Ответ: 5
25. В прямоугольном параллелепипеде известны длины рёбер: , ,  . Найдите площадь сечения, проходящего через вершины
. Найдите площадь сечения, проходящего через вершины 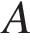 ,
,  и
и  . Ответ: 572
. Ответ: 572
26. В прямоугольном параллелепипеде известны длины рёбер , ,  . Найдите синус угла между прямыми
. Найдите синус угла между прямыми  и
и  .
.
Ответ: 0,6
27. В прямоугольном параллелепипеде известны длины рёбер:  = 3,
= 3,  = 5,
= 5,  = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
= 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Ответ: 39






































