Теория
Блок 1
| Неравенства 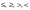 |
| Общее решение – множество всех частных решений неравенства |
Блок 2
| Равносильные неравенства  |
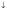
| 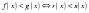
|
| Одинаковые решения или их отсутствие |
Блок 3
| Равносильные преобразования |
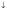
| Правило1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком (не меняя при этом знака неравенства). |
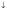
| Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не меняя при этом знака неравенства. |
| Правило 20. Если обе части неравенства с переменной  умножить или разделить на одно и то же выражение умножить или разделить на одно и то же выражение  , положительное при всех значениях , положительное при всех значениях  , и сохранить знак исходного неравенства, то получится неравенство, равносильное данному неравенству. , и сохранить знак исходного неравенства, то получится неравенство, равносильное данному неравенству. |
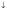
| Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный ( на на  , ,  на на  ). ). |
| Правило 30. Если обе части неравенства с переменной  умножить или разделить на одно и то же выражение умножить или разделить на одно и то же выражение  , отрицательное при всех значениях , отрицательное при всех значениях  , и изменить знак исходного неравенства на противоположный, то получится неравенство, равносильное данному. , и изменить знак исходного неравенства на противоположный, то получится неравенство, равносильное данному. |
Коррекционная карточка
Пример 1.

Пример 2
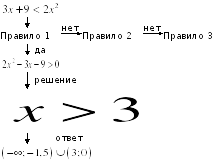
Пример 3. Метод интервалов
 .
.
Найдем корни  =0,
=0,  =0, (х-3)=0, (х+1)=0 , (х+4)=0
=0, (х-3)=0, (х+1)=0 , (х+4)=0
Отметим жирными точками нули числителя и прозрачными точками нули знаменателя, так как знак cравнения не строгий. Если бы знак сравнения был строгим, то все точки были бы прозрачные.


После этого справа налево ведем змейку по следующему правилу: она проходит сверху, меняя знак на нечетной степени и сохраняя знак на четной степени.
Теперь остается выписать ответ:  . Важно не забыть
. Важно не забыть  .
.
Самостоятельная работа.
1вар.-1часть
1. Решите неравенство  .
.
В ответе укажите номер правильного варианта.
1)  2)
2)  3)
3)  4)
4) 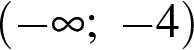
2. Решите неравенство  и определите, на каком рисунке изображено множество его решений.
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
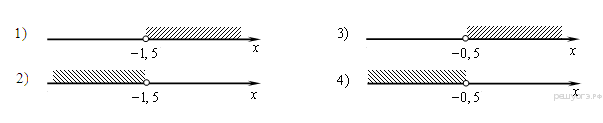
3. Решите неравенство: 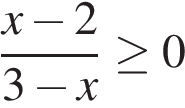
На каком из рисунков изображено множество его решений?
В ответе укажите номер правильного варианта.
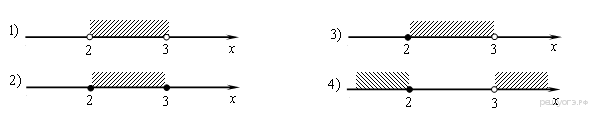
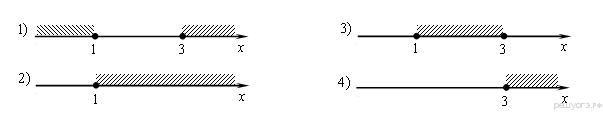
4. На каком рисунке изображено множество решений неравенства 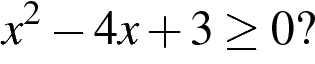
В ответе укажите номер правильного варианта.
5. На каком рисунке изображено множество решений системы неравенств
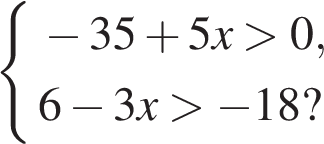
2 вар. –1 часть
1. Решите неравенство  и определите, на каком рисунке изображено множество его решений.
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
2. Решите неравенство
В ответе укажите номер правильного варианта.
1) (−4; +∞) 2) (−12; +∞) 3) (−∞; −4) 4) (−∞; −12)
3. На каком рисунке изображено множество решений неравенства В ответе укажите номер правильного варианта.
4. На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
5. Решите систему неравенств
На каком рисунке изображено множество её решений?
В ответе укажите номер правильного варианта.
1вар- 2 часть
Решите неравенство
Решите неравенство
3. Решите неравенство
4. Решите систему неравенств
5. Решите систему неравенств
2вар.-2часть
Решите неравенство
2. Решите неравенство
3. Решите неравенство
4. Решите систему неравенств
5. Решите систему неравенств
Ответы к самостоятельной :
1в-1ч 2в-1ч 1в -2ч 2в-2ч
4 2 (-∞;-0,75]U[3;+ ∞) (2/3;2)
1 1 (-∞;-3]U[- 1/3;+ ∞) [0,4;4]
3 4 [-1;1] (-∞;-8]U[8;+ ∞)
1 4 (-8;4) [-3;8] 1 2 [-3;5] (-9;-5)





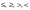
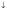



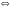
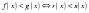
 умножить или разделить на одно и то же выражение
умножить или разделить на одно и то же выражение  , положительное при всех значениях
, положительное при всех значениях  на
на  ,
,  на
на  ).
).
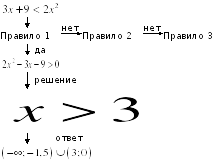
 .
. =0,
=0,  =0, (х-3)=0, (х+1)=0 , (х+4)=0
=0, (х-3)=0, (х+1)=0 , (х+4)=0

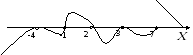
 . Важно не забыть
. Важно не забыть  .
.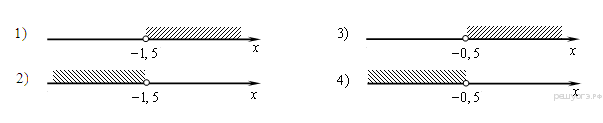
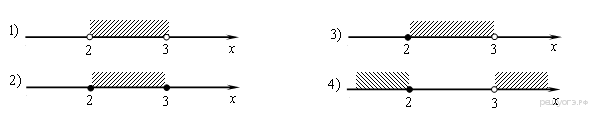

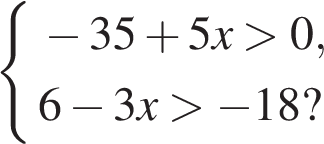
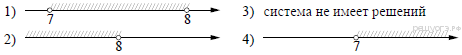
 0 9 8 7 6 5 4 3 2 1 № 2. х 2 – х – 6 0 о х 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 № 3. х 2 – х – 6 -1 -2 -3 -4 -5 -6 № 4. х 2 – х – 6 0" width="640"
0 9 8 7 6 5 4 3 2 1 № 2. х 2 – х – 6 0 о х 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 № 3. х 2 – х – 6 -1 -2 -3 -4 -5 -6 № 4. х 2 – х – 6 0" width="640"
 0 № 1 0. Решите неравенство – х 2 +5 х– 9,6х у = – х 2 + 5 х – 9,6" width="640"
0 № 1 0. Решите неравенство – х 2 +5 х– 9,6х у = – х 2 + 5 х – 9,6" width="640"
 0 3 х № 1 4. Решите неравенство х 2 – 6 х + 9 0" width="640"
0 3 х № 1 4. Решите неравенство х 2 – 6 х + 9 0" width="640"
![Маленький тест ПОДУМАЙ! Решите неравенство х 2 + 4х 7 6 5 4 3 2 1 ВЕРНО! 1 [- 4 ; 0 ] ПОДУМАЙ! ( - 4 ; 0 ) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 4 ПОДУМАЙ!](https://fhd.multiurok.ru/3/c/d/3cd0fd7d3a93ef819449009b52124f82385779a8/img_phpUFKLy9_neravenstva_1_3.jpg)
![Маленький тест ПОДУМАЙ! Решите неравенство х 2 + 4х 0 7 6 5 4 3 2 1 ВЕРНО! ПОДУМАЙ! 1 [- 4 ; 0 ] ( - 4 ; 0 ) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 4 ПОДУМАЙ!](https://fhd.multiurok.ru/3/c/d/3cd0fd7d3a93ef819449009b52124f82385779a8/img_phpUFKLy9_neravenstva_1_4.jpg)










