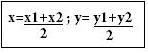Декартові координати на площині
Тема: Відстань між двома точками із заданими координатами. Координати середини відрізка.
Мета: узагальнити та систематизувати знання учнів з теми «Прямокутна система координат»; сформувати поняття відстані між двома точками та середини відрізка в декартових координатах, формувати уміння застосовувати відповідні формули до розв’язування задач; розвивати логічне мислення учнів, виховувати свідоме ставлення до навчання.
Тип уроку: комбінований
Хід уроку
І. Організаційний етап
Перевірка готовності учнів до уроку, налаштування на роботу. (Слайд1)
ІІ. Перевірка домашнього завдання
Зошити по закінченню уроку я зберу та перевірю домашнє завдання.
ІІІ. Мотивація навчання (Формування мети і завдань уроку)
На попередньому уроці ми познайомилися з вами з великим відкриттям у математиці, яке здійснене найвидатнішим мислителем Франції Рене Декартом. (Слайд 2)
Основна його ідея полягає в тому, щоб примусити алгебру, якщо так можна висловитись, працювати на геометрію. (Слайд 3)Як вам відомо, алгебра має справу з числами та рівняннями, а геометрія – з лініями, точками, фігурами. Декарт знайшов спосіб зіставити з геометричними образами, образи алгебри, а потім,виконуючи над ними певні дії, уміти пояснити геометрично їх результати. Можна сказати, що Декарт «перекинув міст», яким з’єднав алгебру з геометрією.
Щоб навчитись описувати геометричні фігури алгебраїчними виразами, потрібно сприйняти й усвідомити матеріал теми «Декартові координати на площині».
Частково з цією темою ви вже знайомі з попереднього уроку та уроків алгебри минулих років. Люди іноді навіть не помічають, як два числа допомагають правильно і швидко орієнтуватися: квиток до театру містить інформацію про певний ряд і номер місця. Залізничний квиток – про номер вагона і номер місця. На полі шахівниці місце будь-якої фігури вказується також двома числами, наприклад, b4.(Слайд 4) Це саме ми бачимо коли граємо в гру «Морський бій».
Отже, тема нашого сьогоднішнього уроку: .(Слайд 5) «Прямокутна система координат на площині. Відстань між двома точками з заданими координатами. Координати середини відрізка». (Записати в зошиті)
Мета уроку: (діти формулюють самостійно) узагальнити та систематизувати відомості про систему координат, дослідити можливість визначення відстані між двома точками та координат середини відрізка в прямокутній системі координат.
ІV. Актуалізація опорних знань учнів
На якому з наведених рисунків зображена координатна пряма? (слайд 6)


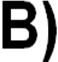

Відповідь:В.
- А чому малюнок А не є координатною прямою?
(На ньому не має одиничного відрізку)
(Не має напрямку)
(Початок променя, напрямок, та одиничний відрізок)
(Слайд 7)
Прочитайте запис:
М (5;3);
Р (-5; 0);
О (0; 0)
(Слайд 8)
Визначте координати точок:
(письмово з подальшою перевіркою
на екрані)
А (-2; 2), В (-1; -4), С (0; -2),
Д (3; 4), Е (0; 0), F (4; 2),
К (4; 0), М (-3;0), Р (3; -2)
(Слайд 9) (письмово з подальшою перевіркою
на екрані)
4. Визначте невідомі координати вершин прямокутника АВСД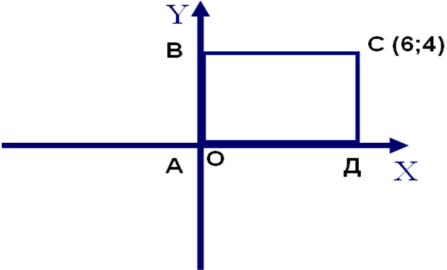
А) А (0;0)
В (0;4)
Д (6;0)

Б) В (-5;3)
Д (5;1)

В) В (2; 6)
Д (10; -2)
(Слайд 10) (усно з подальшою перевіркою
на екрані)
Знайдіть координати точки С
А) С(-1; -1)
Б) С(3;2)
А) Б)
(Слайд 11) (усно з подальшою перевіркою
на екрані)
Точка належить ІVчверті. Які вона має координати за знаком?
( х 0, у
А якщо в І -?
( х 0, у 0 )
В ІІ чверті?
(х 0 )
А в ІІІ чверті?
(х
(Слайд 12) (усно з подальшою перевіркою
на екрані)
Цю тему можна зустріти і на зовнішньому незалежному оцінюванні. Ось ви бачите деякі завдання.
-
1. В яких точках перетинаються графіки функцій? Виберіть правильну відповідь.
А (2;2)
Г (-2;-2)
2. Із запропонованих точок виберіть ті, через які проходить графік даної функції.
В (1;0)
Г (3; -2)
Д (-3;4)
Отже, підведемо підсумок. (Слайд 13)

(Перпендикулярно)
(Вісь абсцис)
(Вісь ординат)
(Початок координат)
(Абсциса та ордината)
(Це дві взаємно перпендикулярні прямі, на яких вибрано початок відліку, одиничний відрізок та додатній напрямок)
Задача (усно)
(Слайд 14) (усно з подальшою перевіркою
на екрані)
Зверніть увагу на ось це завдання. 
Яка фігура накреслена на малюнку?
6
8
Який трикутник?
Як називаються сторони даного трикутника?
Що нам відомо в задачі?
Що знайти?
?
Як можна знайти гіпотенузу?
Чому дорівнює гіпотенуза? (АС = 10)
Задача. (Слайд 15) (усно з подальшою перевіркою
на екрані)
А зараз знайдіть відстань між парами точок, зображених на рисунку:
А) СО - ? (3 од. від.) 
ВО - ? (4 од. від)
СВ - ? (7 од. від)
Б) СМ - ? (2 од. від)
СК - ? (4 од. від)
А як же знайти відстань СА або СВ із заданими координатами?
V. Вивчення нового матеріалу. (Слайд 16)
Отже, дослідимо можливість визначення відстані між двома точками через їхні координати в прямокутній системі координат.
Письмово в зошиті
Дано: А (х1; у1), В (х2; у2)
Знайти: АВ (виразимо відстань між точками через координати цих точок)
Розв’язання
(Слайд 17)

Розглянемо спочатку випадок, коли х1 ≠ х2 і у1 ≠ у2.
Проведемо через точки А і В прямі, паралельні осі координат і позначимо через точку С точку їх перетину.
- Яка фігура утворилася?
- Який трикутник?
- Як називаються сторони трикутника?
- Як знайти гіпотенузу?
Відстань між точками С і В дорівнює Іх1- х2І, а відстань між точками А і С дорівнює Іу1- у2І
За т. Піфагора АВ2= ВС2+АС2
Отже, АВ2 = (х1- х2)2 + (у1- у2)2
Хоча формула для відстані між точками виведена у припущенні х1≠х2 і у1≠у2, вона залишається правильною і для інших випадків. Справді, якщо х1 = х2 , у1≠ у2, то відстань між точками дорівнює Іу1- у2І. Такий самий результат дістанемо і за формулою. Аналогічно розглядається випадок, коли х1 ≠ х2 і у1 = у2. Якщо х1 = х2 і у1 = у2, то точки А і В збігаються і за формулою відстань між ними дорівнює 0.
(Слайд 18)
Відстань між точками позначають d2 = (х1- х2)2 + (у1- у2)2
Координати середини відрізка знаходять за формулами
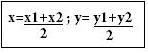
VІ. Засвоєння нових знань і вмінь. (Письмово в зошиті)
(Апостолова Геометрія 9)
Задача 1 (ст.20, завдання 2, № 1(а)
А) АВ = = = на дошці
Б) АВ = = = 10 самостійно
Задача 2 (ст.22, завдання 2, № 29)
х= =4; у = = 1 на дошці
Задача 3 (Слайд 19)
Знайдіть помилки.
Дано: А (3;4); В (2;-1)
Знайти: АВ

 Розв’язання
Розв’язання
АВ = (4 - 2)2 + (4 - 1)2 =
Правильний запис АВ = + =
VІІ. Сам. робота (Слайд 20)
Оберіть посильне для вас завдання
1.На координатній площині зобразіть точки А(3;-1); B(-2;4); C(1;1); D(-3;-2).
2. Знайти координати середини відрізка з кінцями в точках (3;-1) та (-2;-2)
3. Знади відстань від точки В(-2;1) до осі Оy.
4.Знайти відстань від т. А(-5;-2) до осі Ох.
VІІІ. Рефлексія
У якої з точок неправильно позначені координати?(Слайд 21)
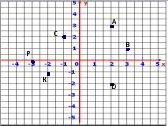
А (2;3); В (3;1); С (-1;2); D (-2;2); Р (0;-3); К (-2;-1)
( Це точки D та Р)
Знайди помилки. (Слайд 22)
А (-145;200) - ІI чверть
В (358;- 422) - ІII чверть
С (218;6203) - І чверть
D (- 139;- 247) - ІV чверть
Е (-371;2108) - ІI чверть
К (953;-712) - ІV чверть
М (-37401;- 40732) - ІII чверть
( Це точки В та D)
Яке з тверджень неправильне? (Слайд 23)
А) Якщо т. А лежить на осі ординат, то її абсциса дорівнює 0.
Б) Якщо т. А збігається з початком координат, то її обидві координати
дорівнюють 0.
В) Точки осі абсцис мають ординати, що дорівнюють 0.
Г) Точка В (-2;-2)належить ІІ чверті.
Відповідь: Г
Чи правильно заповнена таблиця? (Слайд 24)
| Координати точки | (2;3) | (-5;-1) | (-4;6) | (-3;5) |
| Відстань до осі абсцис | 2 | - 1 | 6 | 5 |
| Відстань до осі ординат | 3 | -5 | 4 | 3 |
ІХ Етап. Підсумок уроку. Домашнє завдання. Слайд 25)
Г.В. Апостолова «Геометрія 9» Розділ І. §1-2 вивчити. Ст.20 №1(в); №2(в); №4; №30