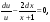Дифференциальные уравнения первого и второго порядков

Однородные уравнения первого порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Уравнение вида , где и – функции от , называется линейным дифференциальным уравнением первого порядка. В частном случае и могут быть постоянными величинами.

Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки , где и – новые функции от .

Пример 1: Найти общее решение уравнения .

Решение: Это линейное уравнение: , . Положим и продифференцируем это равенство по :

Подставив теперь выражения для и в данное уравнение, получим

Так как одну из вспомогательных функций или можно выбрать произвольно, то в качестве возьмем одно из частных решений уравнения . Разделив в этом уравнении переменные и интегрируя, имеем

,

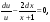
(произвольную постоянную С принимаем равной нулю, так как находим одно из частных решений).

Подставим теперь выражение для , получим уравнение:

или

Отсюда находим

.

Зная и , получаем общее решение данного уравнения:

Пример 2: Найти частное решение уравнения , если при .

Решение: Разделив все члены данного уравнения на , получим уравнение

которое является линейным. Положим и продифференцируем это равенство по :

Подставив теперь выражения для и в данное уравнение, получим

,

Для отыскания получаем уравнение , то есть , откуда

;

Подставляя выражение для , имеем

, или , то есть .

Следовательно, общее решение данного уравнения записывается так:

.

Используя начальные условия , , имеем , откуда. Таким образом, искомое частное решение имеет вид .

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

где и – постоянные величины.

Для отыскания общего решения уравнения составляется характеристическое уравнение

которое получается из уравнения заменой на соответствующие степени , причем сама функция заменяется единицей.

Тогда общее решение дифференциального уравнения строится в зависимости от корней и характеристического уравнения. Возможны три случая:

1. Корни и – действительные и различные. В этом случае общее решение уравнения имеет вид:

.

1. Корни и – действительные и равные: . В этом случае общее решение уравнения имеет вид:

.

1. Корни и – комплексно-сопряженные: , . В этом случае общее решение уравнения имеет вид:

.

Пример 3: Решить уравнение .

Решение: Составим характеристическое уравнение:

Общее решение данного дифференциального уравнения имеет вид:

.

Пример 4: Решить уравнение .

Решение: Составим характеристическое уравнение:

Общее решение данного дифференциального уравнения имеет вид:

.

Пример 5: Решить уравнение .

Решение: Составим характеристическое уравнение:

где – мнимая единица. Общее решение данного дифференциального уравнения имеет вид:

.

Пример 6: Решить уравнение .

Решение: Составим характеристическое уравнение:

Комплексно-сопряженные корни таковы: . Общее решение дифференциального уравнения имеет вид:

.

Пример 7: Найти частное решение уравнения , если и при .

Решение: Составим характеристическое уравнение , откуда , . Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид:

, то есть .

Для нахождения искомого частного решения нужно определить значения постоянных и . Подставив в общее решение значения , , получим .

Продифференцировав общее решение и подставив в полученное выражение значения , , имеем ; . Отсюда находим: . Таким образом, искомое частное решение имеет вид

Задания для самостоятельного решения

1. Найдите общие решения уравнений:

1. Найдите частные решения уравнений, удовлетворяющие укзанным начальным условиям:

1. при

2. при

1. Найдите общие решения уравнений:

1. Найдите частные решения уравнений, удовлетворяющие укзанным начальным условиям:

1. и при .

2. и при .