ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКОЙ ОБЛАСТИ
«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ТЕОРЕТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ
ДИСЦИПЛИНА «МАТЕМАТИКА»
Раздел 1. Математический анализ
Тема 1.4. Основы дифференциального исчисления
Специальность
060101 Лечебное дело
Курс – первый
2013
| Одобрена на заседании цикловой
методической комиссии _________________ Протокол №___от_______________________ Председатель___________________________
Разработчик: О.А. Потемкина ‑ преподаватель второй квалификационной категории
|
ОГЛАВЛЕНИЕ
Выписка из рабочей программы Методический лист | 4 4 |
Примерная хронокарта занятия | 5-6 |
Актуализация опорных знаний (Приложение 1) | 7-8 |
Информационно-справочный материал (Приложение 2) | 9-18 |
Первичное закрепление изученного материала (Приложение 3) | 19 |
Выписка из рабочей программы
дисциплины «Математика»
для специальности 060101 Лечебное дело
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект) | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Тема 1.4. Основы дифференциального исчисления | Содержание учебного материала | 2 |
|
|
| Основы дифференциального исчисления. Производная функции, её геометрический и механический смысл. Таблица производных. Правила вычисления производных функций. Приложение производной. |
| 1,2 |
| Лабораторные работы | ‑ |
|
| Практические занятия 2) Вычисление производных; 3) Геометрические и механические приложения производной; 4) Текстовые задачи на нахождение наибольших и наименьших значений и экстремумов |
2 2 2 |
| Контрольные работы | ‑ |
| Самостоятельная работа обучающихся Выполнение упражнений, решение прикладных задач, работа с обучающими тестами. Работа с учебником [1, стр. 49-74]; [1, стр. 78, задание №15, контрольные вопросы] | 4 |
Методический лист
Вид занятия –комбинированный урок
Продолжительность – 90 мин.
Требования к результатам освоения темы в соответствии с ФГОС по специальности среднего профессионального образования 060101 Лечебное дело:
В результате изучения темы обучающийся должен уметь:
В результате изучения темы обучающийся должен знать:
значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
основные математические методы решения прикладных задач;
основы интегрального и дифференциального исчисления.
Цели занятия:
1. Учебные цели:
рассмотреть понятие приращения функции, производной и мгновенной скорости движения, сложной функции;
рассмотреть правила дифференцирования и использовать их для вычисления производных;
усвоить основной смысл производной, как характеристики быстроты изменения функции;
уяснить возможность использования производной в решении физических, биологических и медицинских задач;
повторить и закрепить навык вычисления производных элементарных функций.
2. Развивающие цели:
способствовать
формированию умений применять приемы сравнения, обобщения, выделения главного;
развитию математического кругозора, мышления и речи, внимания и памяти.
3. Воспитательные цели: содействовать формированию культуры общения, внимания, интереса к предмету, способствовать пониманию студентом сущности и социальной значимости своей будущей профессии, проявления к ней устойчивого интереса.
Методы обучения: объяснительно-иллюстративный, репродуктивный.
Место проведения занятия: аудитория колледжа.
Интегративные связи: физика, геометрия и все предметы, где используется математический аппарат
Литература:
Гилярова М.Г. Математика для медицинских колледжей. – Ростов н/Д: Феникс, 2011. – 410, [1] с. – (Медицина)
Математика: учеб. пособие / В.С. Михеев [и др.]; под ред. Н.М. Демина. – Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).
Оснащение занятия:
Доска
Раздаточный материал
Проектор
Мультимедиа
Домашнее задание:
Конспект
Работа с учебником [1, стр. 49-74]
Примерная хронокарта занятия
| № п/п | Этап урока | Время (мин) | Методические указания |
| 1 | Организационная часть | 2 | Проверка посещаемости и внешнего вида студентов. Сообщение темы, цели и плана занятия. |
| 2 | Мотивация | 3 | «Дифференциальное исчисление» — один из важнейших разделов современной математики, основы которого были заложены во второй половине XVII века английским математиком — механиком Исааком Ньютоном (1643-1727) и немецким ученым Готфридом Вильгельмом Лейбницем (1646-1716). В развитие этого раздела внесли свой вклад многие выдающиеся математики мира. Среди них особое место занимает Леонард Эйлер (1707-1783). Швейцарец по происхождению, Эйлер более 20 лет прожил в России. Здесь он опубликовал более 800 работ по различным разделам математики, среди них около 200 работ — по дифференциальному исчислению. Неоценимый вклад в завершение такого раздела математики, как «Дифференциальное исчисление», внесли французский математик Огюстен Луи Коши, немецкий математик Карл Те́одор Вильге́льм Вейерштрасс и первая русская женщина-математик Соофья Васильевна Ковалевская. Сегодня уже не вызывает сомнения то, что современный врач должен понимать и владеть методами математического описания и обработки медико-биологических процессов и данных. Начальные знания, полученные при изучении данной темы, могут быть применены при составлении и решении дифференциальных уравнений первого порядка на примерах задач медико-биологического содержания (закон растворения лекарственных форм вещества из таблетки, закон размножения бактерий и др.), при определении ошибок (погрешностей) измерений и тд. |
| 3 | Актуализация опорных знаний | 10 | Фронтальный опрос (Приложение 1)
|
| 4 | Изложение нового материала | 35 | План изложения (Приложение 2)
1. Тайны планетных орбит (исторический экскурс) 2. Свойство «линейности в малом» 3. Приращение функции 4. Дифференцируемые функции 5. Определение производной. 6. Правила вычисления производных 7. Сложная функция 8. Производная сложной функции 9. Производная элементарных функций 10. Производная в физике и геометрии 11. Приложения производной к исследованию функции |
| 5 | Практическая часть
Выполнение упражнений для закрепления материала темы | 35 |
(Приложение 3)
Первичное закрепление полученных знаний и умений Осмысление полученных знаний и умений
|
| 6 | Домашнее задание | 2 | Подготовить теоретический материал к практическому занятию работая с конспектом лекции и учебником [1, стр. 49-74] |
| 7 | Подведение итогов занятия | 3 | Выставление оценок, комментируя ошибки, сделанные в ходе работы |
Приложение 1
Актуализация опорных знаний
КОНТРОЛЬНЫЕ ВОПРОСЫ
| Вопрос | Ответ |
Дайте определение предела функции. | Если разность между значениями некоторой функции у = f(x) и постоянным числом а, взятая по модулю, является бесконечно малой функцией, то число а является пределом функции у = f(x), что принято записывать так: 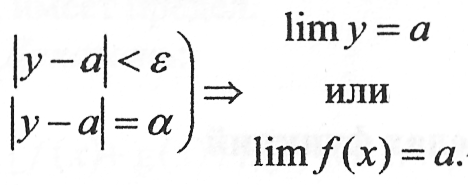
|
Перечислите основные свойства пределов функций. | Теорема 1 (об единственности предела). Если функция имеет предел, то он единственный. Теорема 2 (о пределе суммы n функций). Предел суммы конечного числа функций равен сумме пределов каждой функции в отдельности. Теорема 3. Предел разности двух функций равен разности пределов функций уменьшаемой и вычитаемой. Теорема 4. Предел произведения конечного числа функций равен произведению пределов от каждой функции в отдельности. Следствие 1. Постоянный множитель можно выносить за знак предела или вносить под знак. Следствие 2. Предел от степени некоторой функции равен степени предела этой функции. Следствие 3. Предел от корня n-го показателя некоторой функции равен корню этого показателя из предела этой функции. Теорема 5. Предел частного от деления двух функций равен частному пределов функций делимой и делителя. Следствие 1. Предел от логарифма некоторой функции равен логарифму от предела этой функции. |
Какие вам известны приёмы вычисления пределов функций? | Подстановка числа в функцию. Деление числителя и знаменателя на х в старшей степени. Умножение числителя и знаменателя на сопряжённое. Разложение числителя и знаменателя на множители. |
Какие известны способы раскрытия неопределённости вида ? | Для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на х в старшей степени. |
Какие известны способы раскрытия неопределённости вида ? | Если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители. |
Дайте определение бесконечно малой функции. | Функция f(x) называется бесконечно малой при хх0, если |
Дайте определение бесконечно большой функции. | Функция f(x) называется бесконечно большой при хх0, если |
Как используется теория пределов? | Теория пределов очень активно применяется в экономических расчетах, например, в доказательствах и расчетах, которые связаны с непрерывными процессами; в финансовых рентах. Пределы функции применяются для нахождения асимптот графика функции при ее исследовании. |
Приложение 2
Информационно-справочный материал
1. Тайны планетных орбит
Древнегреческие ученые умели решать лишь немногие задачи кинематики — они могли рассчитать либо равномерное прямолинейное движение, либо равномерное вращение вокруг оси. Но описать движение планет столь простыми способами не удавалось.
Планеты двигались по самым замысловатым кривым, иногда быстро продвигаясь вперед, а иногда замедляя свое движение и даже возвращаясь назад. Чтобы свести эти движения к круговым, александрийский астроном Птолемей, живший в III в. до н. э., придумал сложнейшую систему окружностей; центры малых окружностей равномерно вращались по большим, а планеты равномерно вращались по малым окружностям. Но и система Птолемея не согласовывалась с наблюдениями, и ее приходилось все время усложнять. Лишь в XVII веке немецкому ученому Иоганну Кеплеру удалось на основе созданной великим польским астрономом Николаем Коперником гелиоцентрической системы мира сформулировать законы движения планет.
Оказалось, что планеты движутся не по окружностям, а по эллипсам, и притом неравномерно. Объяснить, почему это так, Кеплер не смог — в то время не были известны ни общие законы механики, ни математические методы, позволявшие изучать криволинейное и неравномерное движение.
Лишь в конце XVII века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические методы, позволявшие сводить неравномерное к равномерному, неоднородное к однородному, криволинейное к прямолинейному. В основе лежала простая идея — движение любого тела за малый промежуток времени можно приближенно рассматривать как прямолинейное и равномерное.
Методы, развитые Ньютоном, дали возможность по заданному закону движения тела находить его скорость и ускорение в любой момент времени, а также решать обратную задачу — по заданному ускорению сначала находить скорость, а потом закон движения тела. А если вспомнить, что по второму закону Ньютона ускорение тела постоянной массы пропорционально действующей на него силе, то станет ясно, что новые методы устанавливали связь между движением тела и действующими на него силами, то есть решали основную задачу механики.
Одновременно с Ньютоном немецкий философ и математик Готтфрид Вильгельм Лейбниц изучал, как проводить касательные к произвольным кривым. Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введенные Лейбницем, оказались настолько удачными, что сохранились и по сей день.
Новая математика Ньютона и Лейбница состояла из двух больших частей — дифференциального и интегрального исчислений. В первом из них говорилось, как, изучая малую часть явления, сводить неравномерное к равномерному, а во втором — как из малых равномерных частей конструировать сложное неравномерное явление.
Дифференциальному и интегральному исчислениям и их дальнейшему развитию (вариационному исчислению, дифференциальным уравнениям, теории функций комплексного переменного и т. д.) посвящены многотомные монографии. Сегодня мы рассмотрим лишь основные понятиях дифференциального исчисления.
2. Свойство «линейности в малом»
Три линии на рисунке 1 являются частями одной и той же параболы у= х2, изображенной в разных масштабах. Рисунок а) сделан в мелком масштабе, рисунок б) — в масштабе покрупнее, рисунок в) ‑ еще крупнее. На всех рисунках взята одна и та же точка М(1; 1) параболы, чтобы можно было изучить поведение кривой в окрестности этой точки.
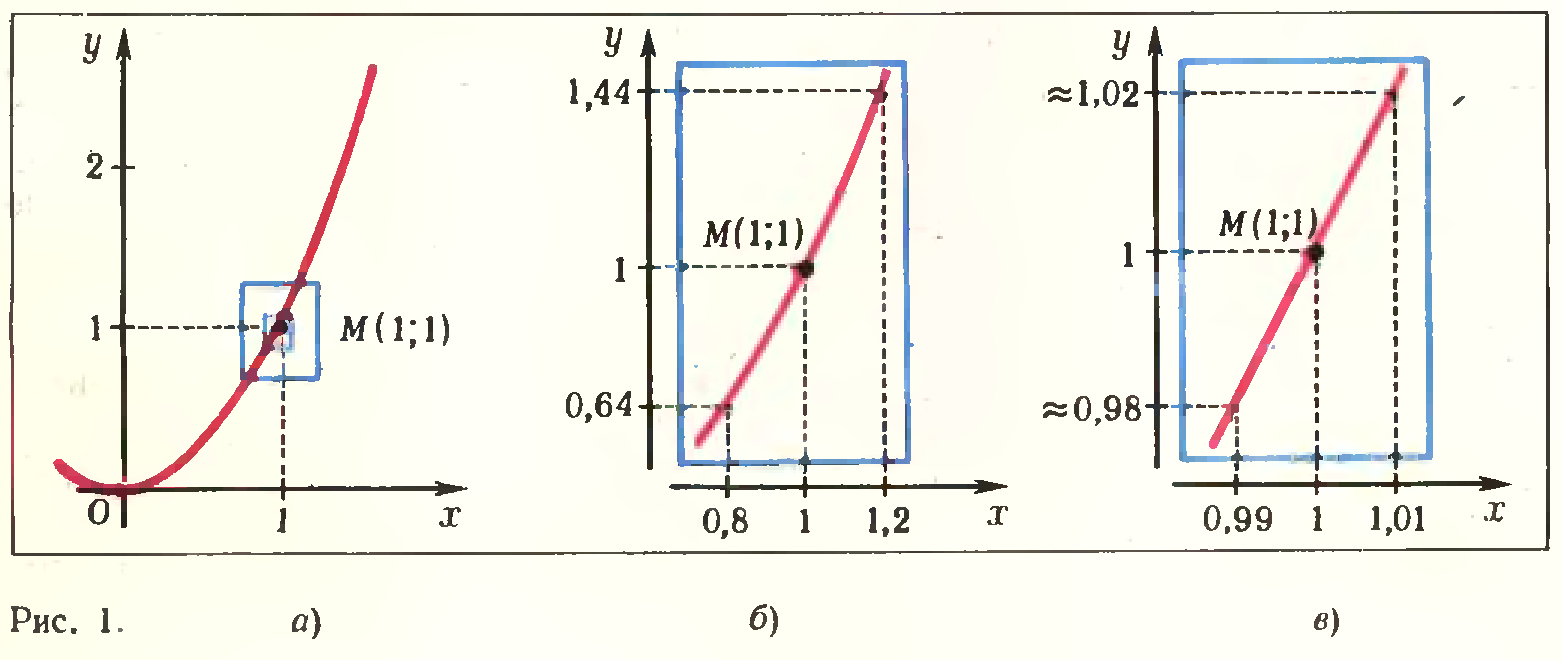
На рисунке 1,а) ясно видно, что парабола искривлена. На рисунке 1,б) это искривление уже менее заметно, а на рисунке 1,в) eго практически нет — график функции у= х2, сделанный в крупном масштабе, на глаз почти неотличим от прямой линии. Чем крупнее мы выберем масштаб, тем меньше график функции у= х2 будет отличаться от некоторой прямой линии, проходящей через точку М(1; 1). То же самое было бы, если бы мы стали строить во все увеличивающемся масштабе график функции у= х2 ‑ в окрестности любой другой точки.
Не только парабола «напоминает» вблизи любой своей точки прямую — этим свойством обладают окружность, гипербола, синусоида и т. д. Его можно назвать свойством «линейности в малом» (термин объясняется тем, что прямая — это график линейной функции у=kx+b).
3. Приращение функции
На рисунке 2 изображен квадрат со стороной длины а; площадь у такого квадрата равна а2. Если длину стороны квадрата увеличить на р, то и площадь увеличится — на величину площади фигуры, закрашенной на рисунке 2. Эту площадь называют приращением площади квадрата. Она равна (а+р)2 – a2, то есть 2ар+р2.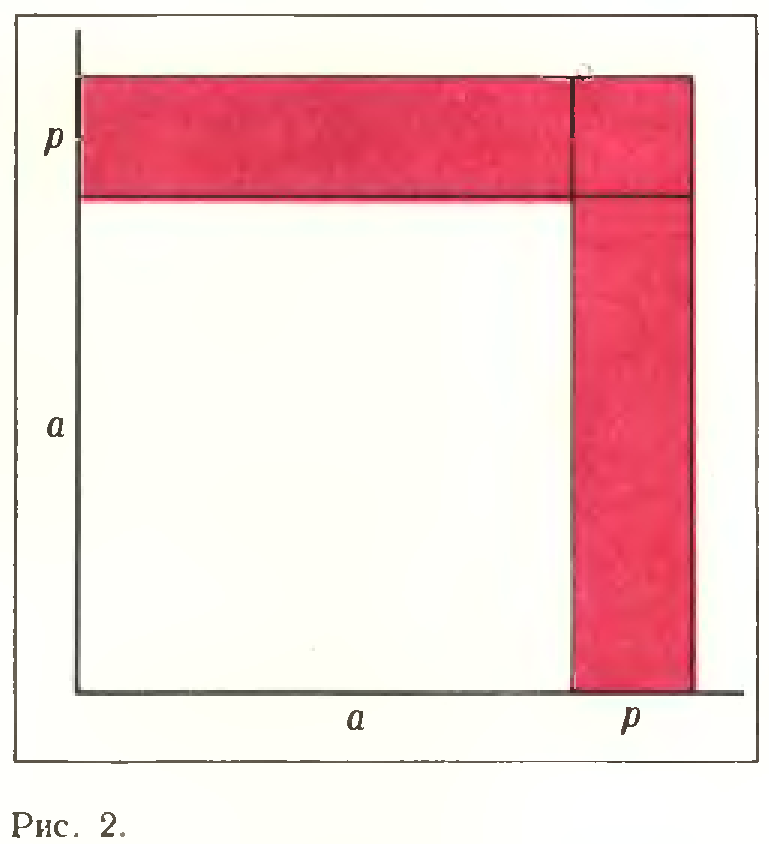
Положим р =х (читается «дельта икс), а приращение площади квадрата обозначим через у.
Получим у = 2ах+(х)2. (1)
Точно так же можно определить понятие приращения для любой функции y=f (х).
Пусть х и х0 — два значения независимой переменной из области определения функции f. Разность х — х0 называется приращeнием независимой переменной в точке х0 и обозначается х (читается: «дельта икс»). Таким образом,
х: = х — х0 ,
откуда следует, что
х = x0 +х.
Говорят, что первоначальное значение х0 независимой переменной «получило приращение х». Вследствие этого значение функции изменится на величину
f(x0) = f(x) – f(x0) = f(x0 +х) – f(x0).
Эта разность между новым значением функции f (х0 + х) и первоначальным ее значением f(х0) называется приращением функции f в точке х0 и обозначается символом f(х0) (читается: «дельта эф в точке x0»), т. е. по определению
f(x0) = f(x0 +х) – f(x0)
f(x0+ х) = f(x0 )+ f(x0).
f(х0) называют также приращением зависимой переменной у и обозначают через f или у.
Обратите внимание на то, что f зависит и от х0 , и от x; а при фиксированном х0 приращение f есть функция от x.
Следовательно, чтобы вычислить приращение функции при переходе от точки х0 к точке х0 +х, нужно:
а) найти значение f(х0) функции в точке х0;
б) найти значение f(х0 +х) функции в точке х0 +х;
в) из второго значения вычесть первое.
Слова «приращение аргумента», «приращение функции» обманчивы: может создаться впечатление, что и аргумент, и функция увеличиваются. На самом деле и x, и y могут быть отрицательными числами. Быть может, было бы лучше вместо «приращение» говорить «изменение», но мы будем придерживаться традиционной терминологии.
Пример 1. Найти x и у в точке ха, если x0 = 2, х = 1,9 и у = х2.
4. Дифференцируемые функции
Теперь уже можно точнее объяснить, почему график функции у=х2 «выпрямляется», когда мы увеличиваем масштаб. Поскольку все рисунки 1, а — в одного и того же размера, то с увеличением масштаба на них умещаются все меньшие и меньшие части кривой. Это означает, что мы рассматриваем нашу функцию при всё меньших и меньших значениях х. Таким образом, «выпрямление» графика функции связано с особым поведением приращения этой функции при уменьшении приращения аргумента.
Чтобы разобраться в этом, выразим приращение функции у=х2 в точке М(1,1) через приращение аргумента.
Мы получим: у =(1+х)2—1 = 2х + (х)2.
Мы видим, что приращение функции состоит из двух слагаемых: 2х и (х)2. Первое из них пропорционально х, а второе обладает следующей особенностью: если х 0, то оно стремится к нулю гораздо быстрее, чем х. Например, если х =0,1, то (х)2=0,01; если х =0,001, то (х)2= 0,000001 и т. д. Таким образом, у при малых х почти равно 2х. Так как у=у—1, х =х—1, то у—12 (х ‑ 1), то есть y2x ‑ 1. Но у=2х—1 — это уравнение прямой с угловым коэффициентом, равным 2. Значит, чем меньшую окрестность точки М (1; 1) мы берем, тем теснее в этой окрестности парабола примыкает к прямой у=2х—1. Говорят, что парабола у=х2 в точке М (1; 1) касается прямой у=2х—1.
Итак, «выпрямление» графика функции у=х2 при увеличении масштаба штаба оказалось связанным с возможностью разложения приращения функции на два слагаемых, из которых одно пропорционально приращению аргумента, а второе при малых значениях х пренебрежимо мало по сравнению с х. Но слова «пренебрежимо мало» еще нуждаются в уточнении.
Будем говорить, что величина пренебрежимо мала по сравнению с х при стремлении х к нулю, если ее отношение к х стремится к нулю: где
Теперь мы уже можем сформулировать основное определение.
Определение 1. Функция у = f(x) называется дифференцируемой в точке а, если ее приращение в этой точке можно представить в виде суммы двух слагаемых, первое из которых пропорционально приращению х аргумента, а второе пренебрежимо мало по сравнению с х.
Иными словами, у = А х +х, (3) где А — число, а стремится к нулю, когда х стремится к нулю.
Коэффициент А в равенстве (3) зависит от того, в какой точке мы его вычисляем. Например, для функции у=х3 в точке а= l имеем А = 3, а в точке а = 2 имеем А = 12. Если считать значение аргумента, для которого вычисляется коэффициент А, переменным, то удобно обозначить его буквой х. При изменении х коэффициент А является функцией от х. Эта функция называется производной от функции y=f (x) и обозначается f’(x), или у' (читается «эф штрих от икс», «игрек штрих»).
Слагаемое Ах, то есть f’(x) х называют дифференциалом функции у= f (x) и обозначают dy. Таким образом, dy = f’(x) х. Обычно х обозначают dx и пишут dy = f'(x) dx.
Из определения 1 следует, что при значениях х, близких к нулю, приращение дифференцируемой функции у почти пропорционально приращению аргумента. Точнее, для такой функции у =(А+) х, где слагаемое а, характеризующее отклонение от «точной» пропорциональности, стремится к нулю, когда х стремится к нулю. Эта «почти пропорциональность» приращения функции приращению аргумента и лежит в основе «выпрямления» графика при увеличении масштаба изображения. 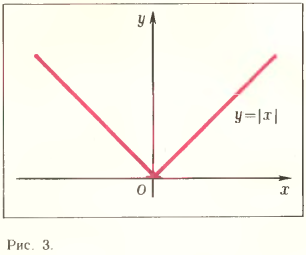
Не следует думать, что все функции дифференцируемы в любой точке. Дифференцируемость, говоря наглядно, означает возможность заменить график функции в окрестности точки прямой линией. Если же график функции имеет в некоторой точке излом, а тем более — разрыв, то функция не будет дифференцируемой в такой точке. Например, функция у= |х | не является дифференцируемой в точке О(0; 0) (рис. 3).
Точки, в которых данная функция у= f (x) не является дифференцируемой, не могут лежать слишком густо — не может же кривая иметь излом в каждой своей точке! Во многих учебниках математики XIX века это утверждение так и было сформулировано. Каково же было изумление ученых, когда во второй половине XIX века немецкий математик Карл Вейерштрасс опубликовал пример функции, непрерывной во всех точках, но нигде не дифференцируемой! График этой функции имел излом в каждой своей точке. Позже выяснилось, что за несколько лет до Вейерштрасса функцию с таким же свойством построил чешский математик Бернард Больцано; эта работа Больцано была опубликована лишь через много лет после его смерти.
5. Определение производной
С производными вы по существу уже встречались в курсе физики IX класса, где мгновенная скорость в момент времени t0 определялась как предел в точке t0 средней скорости за промежуток времени [t0; t0 + t]:
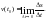
По аналогии со средней и мгновенной скоростью движущегося тела, средней скоростью изменения функции на промежутке [х0; х0 + х] называется отношение приращения функции к приращению независимого переменного:
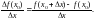
Предел средней скорости при стремящемся к нулю приращении независимого переменного, т. е.
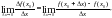
называется скоростью изменения функции в точке х0. Для скорости изменения функции в точке х0 принято название производная.
Определение. Производной функции f в точке х0 называется
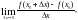
Производная функции f в точке х0 обозначается f ’(х0) (читается: «эф штрих в точке х0»). Таким образом, по определению: 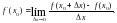
Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Эта функция называется производной функции f и обозначается f' или f'(x). Нахождение производной данной функции называется дифференцированием.
Пример 2. Найдем производную функции f(х) = х2.
По определению производной функции в точке имеем:
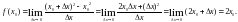
Этот результат принято записывать так:
(х2)’=2х.
6. Правила вычисления производных
Существует несколько полезных правил для нахождения производных, которые мы сформулируем в виде теорем. При этом предполагается, как и в теоремах о пределах, что рассматриваемые далее функции определены в некоторой окрестности точки х0.
Теорема 1. Если функции и и v дифференцируемы в точке х0, то их сумма дифференцируема в этой же точке и
(и + v)' = и' + v'.
Коротко говорят: производная суммы равна сумме производных.
Производная разности равна разности производных.
Теорема 2. Если функции и и v дифференцируемы в точке х0, то их произведение дифференцируемо в этой же точке и
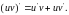
Следствие. Если функция и дифференцируема в точке х0, а С — постоянная, то функция Си дифференцируема в этой точке и
(Си)' = Си'.
Коротко говорят: постоянный множитель выносится за знак производной.
Теорема 3. Если функции и и v дифференцируемы в точке х0 и функция v не равна нулю в этой точке, то частное 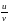 тоже дифференцируемо в этой точке и
тоже дифференцируемо в этой точке и
Теорема 4. Для любого целого п и любого x (х 0 при n1)
(xn)’=nxn-1.
Задание №1. Найдите производные функций используя правила вычисления производной
7. Сложная функция
Напомним, что числовая функция есть отображение одного числового множества (области определения функции) на другое числовое множество (область значений функции). В геометрии мы рассматривали композиции отображений. Теперь мы займемся применениями этого понятия к числовым функциям.
Пример 3. Пусть требуется вычислить по заданному х соответствующее значение z функции f заданной формулой: 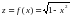
Для этого мы вычислим сначала по заданному х значение
y=g(x)=1 – x2,
а затем уже по этому у вычисляется 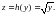
Итак, функция g отображает х в у, а функция h отображает у в z = f(х), т. е. отображение f есть композиция отображений g и h: f = h g, как это принято записывать в учебнике геометрии.
Говорят также, что f есть сложная функция, составленная из функций g и h, и пишут:
f(x)=h(g(x)).
Чтобы вычислить значение сложной функции, соответствующее какому-либо значению переменной х, сначала вычисляют соответствующее значение «промежуточной переменной»
у = g(х), а затем h (у).
8. Производная сложной функции
Представлять заданную функцию h в виде сложной, составленной из более простых и известных функций, удобно не только при вычислении значений функции, но и при нахождении производной.
Итак: если функция f(x)=h(g(x)) имеет производную в точке x0, то её производная находится по правилу:
Пример 4. Найдем производную функции f (х) = (2х + 3)100.
Функция h представима в виде сложной функции: g(x)= (2х + 3), где h (g) = g100. По формуле имеем:
f’(х) = 2 · 100 = = .
9. Производная элементарных функций
| № | Функция | Производная | № | Функция | Производная |
| 1 | C | C'=0 | 11 | sin u | (sin u)’= cos u · u’ |
| 2 | kx+b | (kx+b)’=k | 12 | cos u | (cos u)’ =- sin u · u’ |
| 3 | x | (x)’=1 | 13 | tg u | = |
| 4 |
|
| 14 | ctg u |
|
| 5 |
|
| 15 | arcsin u |
|
| 6 |
|
| 16 | arccos u |
|
| 7 |
|
| 17 | arctg u |
|
| 8 | ln u |
| 18 | arcctg u |
|
| 9 | lg u |
| 19 | au | (au)’= au·ln a·u’ |
| 10 | loga u |
| 20 | eu | (eu)’= eu · u’ |
10. Производная в физике и геометрии
Производные находят самое широкое применение при решении задач в физике и геометрии.
В основе задач, которые решаются с помощью производных (первой и второй), лежат положения, разработанные создателями раздела математики «Дифференциальное исчисление» английским механиком-математиком И. Ньютоном и немецким учёным Г. Лейбницем.
Производная в физике
В основе задач, которые решаются в физике с помощью производных (первой и второй), лежат следующие утверждения одного из создателей дифференциального исчисления И. Ньютона:
Находя первую производную от функции, мы решаем очень важную физическую задачу, а именно: определяем быстроту изменения функции, т.е., собственно, скорость!
Таким образом, по Ньютону: 
есть скорость функции.
Применительно к движению, если s = f(t) или х = f(t) — закон движения тела (точки), который позволяет найти положение тела (точки) или пройденный ими путь для любого момента времени, то их скорость:
2. Находя вторую производную от функции, мы определяем быстроту изменения её скорости, т.е. ускорение функции.
Применительно к движению, если известен закон движения тела(точки s = f(t) или x = f(t), то , где а — ускорение точки (тела)
Получаем:
Итак, по Ньютону: если s = f(t) — закон движения тела, то его скорость (скорость для любого момента времени):
V=S’(t) ; a= v’(t).
По существу, Ньютон ответил на вопросы, которые стояли перед механиками почти два тысячелетия — как рассчитывать скорость и ускорение движущихся тел в любой момент времени. Эти скорость и ускорение называются мгновенными.
Задание №2. Решите задачу.
Тело движется прямолинейно по закону s = (t в секундах, s в метрах). Найти скорость и ускорение тела через 5 секунд после начала движения.
Производные в геометрии
Выдающийся немецкий ученый Г.В. Лейбниц к понятию производной функции у = f(x) применил геометрический подход. Его интересовали два вопроса:
1. Как находить угол наклона касательной, проведенной к графику функции у = f(x) в точке графика с абсциссой х = х0 ?
2. Каким уравнением описывается эта касательная?
По существу, ответы на эти вопросы, которые дал Лейбниц, и легли в основу дифференциального исчисления.
Лейбниц доказал следующее. Пусть задана некоторая функция у = f(x) и она имеет график, изображенный на рис. 1,
Возьмем на нем произвольную точку М, абсцисса которой х = х0, а ордината f(x0) (см. рис. 2), и проведем через эту точку касательную к графику у = f(x), которая образует с осью абсцисс угол (его называют углом наклона касательной).
Тогда тангенс угла наклона касательной к графику функции у = f(x) в точке с абсциссой х = х0 есть , т.е. производная функции.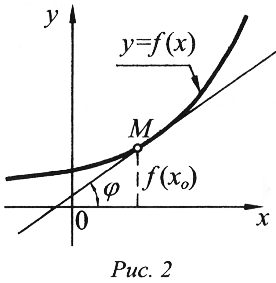
Таким образом: tg =f’(x0)
Следовательно, с точки зрения геометрии, производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику данной функции у = f(x) в данной точке.
В этом заключается геометрический смысл производной функции.
2. Уравнение касательной к графику функции у =f(х) в точке графика с абсциссой х = х0 имеет вид: y=f(x0) + f’(x0) · (x - x0)
Такая трактовка первой производной В. Лейбницем позволила сравнительно легко решать множество задач «чистой» математики, связанных с промежутками монотонности, экстремумами функции, графиками.
Задание №3. Решите задачи.
а) Найдите тангенс угла наклона касательной, проведённой к графику функции y = 1+ 2х – 3х2 в точке с абсциссой х0 = -1.
б) Написать уравнение касательной, проведённой к графику функции f(x) = x2 - 4x +3 в точке х0 = 1.
11. Приложения производной к исследованию функции
Монотонность функции. Исследование функций на монотонность с помощью производной
Прежде всего, вспомним, что функция у = f(x) называется монотонной на промежутке х(а;b), если она на этом промежутке или только возрастает, или только убывает.
Часто в математике приходится находить эти промежутки. Оказывается, что с помощью производной очень легко находить промежутки возрастания или убывания функции или, как принято говорить в математике, исследовать функцию на монотонность. Исследовать функцию на монотонность — это значит найти промежутки значений аргумента, на которых данная функция или возрастает, или убывает.
Если 1-я производная функции y = f(x) в промежутке значений аргумента х(а;b) существует и положительна, то эта функция в заданном промежутке возрастающая.
Это и есть, как говорят, необходимое и достаточное условие возрастания функции на промежутке, что кратко можно записать так:
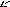 f '(x)0y = f(x) на соответственном промежутке.
f '(x)0y = f(x) на соответственном промежутке.
Отсюда следуют действия над функцией для определения её промежутков возрастания:
1. Найти 1-ю производную функции у = f(x);
2. Решить неравенство f '(x) 0.
Решение этого неравенства и есть промежуток возрастания данной функции.
Аналогично рассуждаем и для промежутков убывания.
В точках экстремума первая производная функции равна нулю.
Задание №4. Решите задачу.
Определите экстремумы и промежутки монотонности функции y= x3 - 6x2 +4
Приложение 3
Первичное закрепление изученного материала
|
|
| Задание №1. Найдите производные функций используя правила вычисления производной
|
|
|
|
| Задание №2. Решите задачу. Тело движется прямолинейно по закону s = (t в секундах, s в метрах). Найти скорость и ускорение тела через 5 секунд после начала движения.
|
| Задание №3. Решите задачи. а) Найдите тангенс угла наклона касательной, проведённой к графику функции y = 1+ 2х – 3х2 в точке с абсциссой х0 = -1. б) Написать уравнение касательной, проведённой к графику функции f(x) = x2 - 4x +3 в точке х0 = 1.
|
Эталоны ответов
| Задание №1 ; ; ; |
| Задание №2 v = 160 м/с а= 62 м/с2 |
| Задание №3 а) tg = 8 б) |






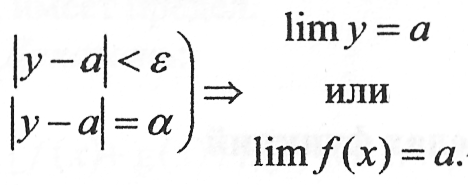



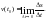
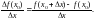
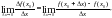
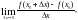
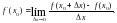
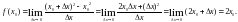
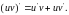
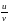 тоже дифференцируемо в этой точке и
тоже дифференцируемо в этой точке и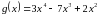
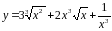
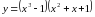
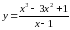

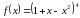
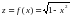
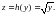



 f '(x)0y = f(x) на соответственном промежутке.
f '(x)0y = f(x) на соответственном промежутке.









