Департамент образования мэрии города Новосибирска
Дворец творчества детей и учащейся молодежи «Юниор»
Городская открытая научно-практическая
конференция НОУ «Сибирь»
Направление: математика
Диофантовы уравнения
Автор: Васильева Юлия Вячеславовна, 10в
МБОУ «Гимназия №13 имени Э. А. Быкова»
Центральный округ г. Новосибирска
Консультант проекта: Давыдова Татьяна
Николаевна, учитель математики,
Контактный телефон руководителя:
8-923-705-52-97
Новосибирск 2021
СОДЕРЖАНИЕ
Введение…………………………………………………………………………..3
Актуальность выбранной темы………………..………………………………...3
Теоретическая часть……………………………………………………...............4
Сведения из истории..…………………………………………………………4
Задачи, приводящие к диофантовым уравнениям…………..……………….5
Пример 1 «Фазаны и кролики»……………………………………………5
Пример 2 «Гвозди и ящики»………………………………………………5
Пример 3 «Марки и копейки»……..……………………………………….6
Пример 4 «Пифагоровы тройки»……….………………………………….7
Практическая часть...…………………………………………………………….9
Метод 1………………………………………………………………………...9
Метод 2………………………………………………………………………...9
Метод 3………………………………………………………………………..10
Метод 4………………………………………………………………………..11
Метод 5………………………………………………………………………..11
Метод 6………………………………………………………………………..11
Метод 7………………………………………………………………………..12
Заключение……………………………………………………………………….13
Список литературы………………………………………………………………14
ВВЕДЕНИЕ
Актуальность выбранной темы
Диофантовым уравнениям мало времени уделено в курсе школьной программы, хотя многие задачи можно решать, как раз с помощью них. Это значит, дополнительные знания о диофантовых уравнениях способны не только расширить кругозор ученика, но и быть очень полезными.
Уравнения в целых числах присутствуют в качестве заданий практически на каждой олимпиаде школьников по математике. Существует много методов их решения, которые не входят в школьную программу по математике, однако их полезно знать школьникам.
Цель моей работы - формирование знаний о типах диофантовых уравнений и основных методах решения в аспекте их реализации в школьной программе и при подготовке к олимпиадам.
Задачи:
1. Изучить историю возникновения диофантовых уравнений.
2. Подобрать задачи из школьного курса, которые могут быть решены при помощи диофантовых уравнений.
3. Познакомиться с различными типами диофантовых уравнений и методами их решения.
4. Выбрать диофантовы уравнения, которые наиболее приемлемы для применения на школьных уроках и дополнительных занятиях.
Гипотеза: Диофантовы уравнения могут быть применены для решения изучаемых в школе задач.
Так что же такое диофантовы уравнения?
Диофантовыми уравнениями принято называть уравнения с целыми коэффициентами, содержащие две или более неизвестных, которые требуют целочисленного решения. Своё название они получили в честь античного учёного Диофанта, который занимался решением подобных уравнений.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Сведения из истории
О жизни Диофанта известно достаточно мало, изначально промежуток времени, в котором мог жить Диофант шёл от середины II века до н. э до середины IV века н. э, но благодаря трудам французского историка Поля Таннери этот промежуток сузился до середины III века н. э. Жил Диофант в городе Александрия, а его возраст можно узнать из дошедшего до нашего времени стихотворения-загадки:
Прах Диофанта гробница покоит; дивись ей — и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребёнком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
По этому стихотворению можно составить уравнение с одной неизвестной: 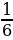 х+
х+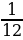 х+
х+ х+5+
х+5+ х+4=х решением данного уравнения будет число 84. Известным трудом Диофанта является «Арифметика», из которой до нас дошло лишь 6 из 13 книг, где он не только расписал методы решения 189 задач, но и придумал обозначения для неизвестных и некоторых математических знаков. Так же Диофант придумал такие приёмы решения уравнений, как: перенос неизвестных в одну сторону уравнения и приведение подобных членов. И, конечно, в его работах были приведены уравнения с двумя или более неизвестными, целыми коэффициентами и решением в целых числах.
х+4=х решением данного уравнения будет число 84. Известным трудом Диофанта является «Арифметика», из которой до нас дошло лишь 6 из 13 книг, где он не только расписал методы решения 189 задач, но и придумал обозначения для неизвестных и некоторых математических знаков. Так же Диофант придумал такие приёмы решения уравнений, как: перенос неизвестных в одну сторону уравнения и приведение подобных членов. И, конечно, в его работах были приведены уравнения с двумя или более неизвестными, целыми коэффициентами и решением в целых числах.
Решением подобных уравнений после Диофанта занималось ещё много людей. Индусские математики примерно с V века использовали такие уравнения для решения проблем возникающих в астрономии. У Брахмагупты – индийского мудреца V века, так же встречалось решение уравнений, подобных диофантовым.
В Европу диофантовы уравнения попали примерно в 16-17 веке. В работе Рафаэля Бомбелли, итальянского профессора университета, 1572 года - «Алгебра» было представлено 143 задачи из «Арифметики» Диофанта. «Арифметика» стала известна в Европе в XVI веке, а в 1621 году она была издана во Франции. И произвела впечатление на Пьер де Ферма – французского математика, одного из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. Свои открытия Ферма часто записывал на полях «Арифметики», а самым известным его трудом стала Великая Теорема Ферма, записанная на полях «Арифметики» в 1637 году, решение к ней Ферма опубликовано позже, но только, для n=4. Эта теорема по сей день интересует математиков, но её доказательство в 1994 году уже было разобрано Эндрю Уайлсом.
Помимо Ферма, разбором диофантовых уравнений занимались такие классики математики, как: Франсуа Виет, Леонард Эйлер, Жозеф Луи Лагранж и многие другие. По сей день решение диофантовых уравнений интересует многих людей.
Рассмотрим некоторые задачи, которые можно легко решить при помощи диофантовых уравнений.
Пример 1. «Фазаны и кролики»
В контактном зоопарке, в клетке, сидели фазаны и кролики, мальчик подошедший к клетке насчитал 18 голов и 50 ног. Сколько в клетке сидело фазанов и сколько кроликов?
Решение: Возьмём количество кроликов за x, а количество фазанов за y. Тогда по условию задачи x+y=18. Как известно, у кролика 4 ноги, а у фазана их 2, значит количество всех ног у кролика равно 4x, а у фазана 2y, мы получаем уравнение 4x+2y=50. Мы получаем систему уравнений, которую можно решить, выразив у через х. Получаем:
у = 18 – х
Подставим это уравнение вместо у во второе уравнение.
4х + 2(18 – х) = 50
4х + 36 – 2х = 50 – переносим 36 вправо.
4х – 2х = 50 – 36
2х = 14
х = 7
Подставим известное нам у в уравнение у от х.
у = 18 – х
у = 18 – 7
у = 11
Ответ: х = 7, у = 11.
Интересно, что из уравнения у =18 – х следует, что х может принять любые значения, но при этом две неизвестные не могут быть выражены ни дробными ни отрицательными числами, ведь это число фазанов и кроликов. Это только подразумевается в задаче, но не сказано в записи х + у = 18, а зная это дополнительное условие иногда можно обойтись и без второго уравнения, получив удовлетворяющий результат из одного уравнения с двумя неизвестными переменными.
Пример 2. «Гвозди и ящики»
На складе есть гвозди в ящиках по 16, 17 и 40кг. Может ли кладовщик выдать 100 кг. гвоздей, не вскрывая ящики?
Попробуем решить задачу составив уравнение, как в первой задаче, за х возьмём количество ящиков по 16 кг, за y количество ящиков по 17 кг, а за z количество ящиков по 40 кг., мы получим уравнение:
16х + 17у + 40z = 100
Что делать с этим уравнением, непонятно. Попробуем прибегнуть к методу подбора.
Взять 3 ящика по 40 не выйдет, это будет 120 кг, что больше 100. Если взять 2 ящика по 40 (80 кг) из 100 у нас останется 20 кг, а это невозможно взять ящиками по 17 или 16. Возьмем 1 ящик по 40 кг и 1 по 17 кг, останется 43 кг, а это число невозможно выдать ящиками по 16 кг, тогда возьмём 1 ящик по 40, 2 ящика по 17, останется 26 кг, а это невозможно взять ящиками по 16 кг. Если взять 1 ящик по 40 и 3 ящика по 17, останется всего 9 кг – это число кг нельзя взять ящиком по 16 кг. Выходит, ящики по 40 не нужны, а комбинировать остаётся ящики по 16 и 17 кг, получается уравнения 16х + 17у = 100, попробуем решить его методом подбора, будет брать ящики по 17 кг в числе от 1 до 5(17●5=85 – максимально близкое число к 100, делящиеся на 17 без остатка) если разность между 100 и числом кг в ящиках по 17 кг будет делиться на 16 – решение есть, если не будет – решения нет. 1 ящик по 17 кг – остаток 83, на 16 не делится, 2 ящика по 17 кг – остаток 66 на 16 не делится, 3 ящика по 17 кг – остаток 49, на 16 не делится, 4 ящика по 17 кг – остаток 32 делится на 16 и получается 2. Выходит 4 ящика по 17 кг и 2 ящика по 16 – единственный верный ответ (если взять 5 ящиков по 17 кг, остаток получится 15, что нам не подходит). Эту задачу можно было решить иными путями, например, как мы делали в первой или взять 6 ящиков по 16 кг, выходит число 96, что на 4 меньше 100, а значит вместо 4 ящиков по 16 кг, нам надо 4 ящика по 17 кг.
Пример 3. «Марки и копейки»
У мальчика было 50 копеек, на которые он хотел купить марки. В киоске были марки только по 4 и 3 копейки, но сдачи у кассира не было. Сколько марок по 4 и 3 копейки нужно взять мальчику, чтобы не осталось сдачи?
Эту задачу можно решить, как 2-ую – методом подбора, но в отличии от второй, у нас выходит несколько решений: 2 марки по 4 копейки и 14 марок по 3 копейки; 5 марок по 4 копейки и 10 марок по 3 копейки; 8 марок по 4 копейки и 6 марок по 3 копейки; 11 марок по 4 копейки и 2 марки по 3 копейки.
Все представленные выше задачи чем-то похожи, и подобные им часто встречаются в жизни. Так же каждая из этих задач имеет два или более неизвестных, целые коэффициенты, и требуют решения в целых числах (ведь у нас не может быть половина кролика в зоопарке, нельзя купить половину марки или вскрыть ящик по условию) значит, по определению, диофантово уравнение, оно было необходимо нам для решения всех этих задач. Все рассмотренные нами уравнения Диофант записал бы так:
аx + by = c
Где a, b и c – целые числа и ответ должен быть дан только в целых числах.
Вот мы и приходим к выводу, что диофантовы уравнения встречаются как в жизни, так и в школьной программе, но при этом нам не известны алгоритмы решения таких уравнений разных типов, только первую задачу мы смогли решить по алгоритму, остальные же, решены методом подбора, именно поэтому я занялась изучением разных типов диофантовых уравнений и их методов решения.
Пример 4. «Пифагоровы тройки»
 Если стороны треугольника пропорциональны числам 3,4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения прямых углов на местности в древнем Египте: на веревке на равном расстоянии друг от друга завязывали узлы. В точке C, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали второй колышек в точке B(CB=4) и натягивали веревку так, чтобы AC=3,AB=5.Треугольник с такими длинами сторон называют египетским.
Если стороны треугольника пропорциональны числам 3,4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения прямых углов на местности в древнем Египте: на веревке на равном расстоянии друг от друга завязывали узлы. В точке C, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали второй колышек в точке B(CB=4) и натягивали веревку так, чтобы AC=3,AB=5.Треугольник с такими длинами сторон называют египетским.
A
C
B
Безошибочность такого построения следует из теоремы, обратной теореме Пифагора: если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным. И действительно, 32+42=52. Говоря иначе, числа 3,4,5-корни уравнения:
х2+у2=z2,
где x – длина первого катета (АС);
y – длина второго катета (СВ);
z – длина гипотенузы (АВ).
На основе этого факта можно составить задачу: Есть ли у уравнения x2+y2=z2 другие целочисленные решения, помимо 3, 4, 5? Можно ли, взяв произвольно одно из чисел, указать остальные два? Какие числа нужно брать, что бы длина обоих катетов и гипотенузы выражалась в целых числах? Такие вопросы интересовали еще мудрецов Древнего Вавилона. Они нашли ответы на них. Знал это и Пифагор. Один из путей решения уравнения x2+y2=z2 в целых числах оказался довольно простым. Запишем подряд квадраты натуральных чисел, отделив друг от друга запятой. Под каждой запятой запишем разность между последовательными квадратами:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196,……576, 625 ……
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, ....49……
Но составлять такие последовательности квадратов долгое и трудоёмкое занятие, поэтому были придуманы формулы, по которым можно находить такие тройки чисел:
Если x-нечетное число, то y=(x2-1):2 и z=(x2+1):2. В этом случае равенство х2+у2=z2 выполняется. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровы тройки».
По этому правилу можно получить уже известные нам тройки: если X=3, то y=(9-1):2=4, z=(9=1):2=5, получилась первая пифагорова тройка; x=5, то y= (25-1):2=12, z=(25+1):2=13, вторая тройка; x=7, то y= (49-1):2=24, z= (49+1):2=25. Других мы пока не знаем, но следующее за 7 нечетное число 9, тогда y=40, z=41. Проверим наши вычисления:
92+402=412
81 + 1600 = 1681 - верно
Следующим шагом было установление правила вычисления всех, а не только некоторых пифагоровых троек. Перепишем уравнение Пифагора следующим образом:
x2=z2-y2;
x2=(z+y)(z-y);
Это и означает, что число x должно разлагаться на два неравных множителя z+y и z-y, которые мы обозначим так, что получится такая система:
z+y=2a2,
z+y=2b2;
Почему написаны коэффициенты 2 и почему написаны квадраты, а не просто числа a и b? Это сделано с целью получить аккуратные ответы. Решив эту систему, получим: (при этом надо иметь в виду, что a b)
z=a2+b2, y=a2-b2, x=2ab
Из этого следует, что наименьшим значением числа b может быть только единица, тогда наименьшим значением a будет 2. Вычислим x, y, z. Получается z=5, y=4, x=3, это уже известный нам «египетский треугольник». А теперь составим таблицу:
Таблица 1 - Длины сторон (целочисленные) прямоугольных треугольников
| b a | 2 | 3 | 4 | 5 | 6 |
| 1 | 3,4,5 | 6,8,10 | 8,15,17 | 10,24,36 | 12,35,37 |
| 2 | ------- | 5,12,13 | 12,16,20 | 20,21,29 | 24,32,40 |
| 3 | 5,12,13 | ------- | 7,24,25 | ------- | 27,36,45 |
| 4 | 12,16,20 | 7,24,25 | ------- | ------- | ------- |
Ясно, что таблицу можно расширить и вправо, и вниз. Подчеркнем главное - уравнение решено, мы знаем способ вычисления всех возможных целочисленных значений длин сторон прямоугольных треугольников.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Изучая источники литературы, я выяснила, что условно можно выделить следующие методы решения диофантовых уравнений: метод полного перебора всех возможных значений переменных, входящих в уравнение; метод разложения на множители; метод, основанный на выражении одной переменной через другую и выделении целой части дроби; методы, основанные на выделении полного квадрата; метод решения уравнения с двумя переменными как квадратного относительно одной из переменных; метод, основанный на оценке выражений, входящих в уравнение; метод, основанный на алгоритме Евклида; метод, основанный на теории цепных дробей; метод, основанный на теории сравнений; метод бесконечного спуска и др. Я познакомилась с некоторыми методами, которые можно применять в школьной практике, а также при подготовке к олимпиаде.
1. Метод полного перебора всех возможных значений переменных, входящих в уравнение
Пример 1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения: 49x + 51y = 602.
Решение. Выразим из уравнения переменную x через y, x = (602−51y)/49 , так как x и y – натуральные числа, то x = (602−51y)/49 ≥ 1, 602 − 51y ≥ 49, 51y ≤ 553, 1 ≤ 1043/51. Полный перебор вариантов показывает, что натуральными решениями уравнения являются x = 5, y = 7.
Ответ: (5; 7).
Пример 2. Решить уравнение 3x 4y 1 в целых числах.
Решение: Перепишем уравнение в виде 3x 4y 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть.
Рассмотрим три случая:
1) Если y 3m , где mZ , то 4y 1 12m 1 не кратно 3.
2) Если y 3m 1 , где mZ , то 4y 1 4(3m 1) 1 12m 5 не кратно 3.
3) Если y 3m 2 , где mZ , то 4y 1 4(3m 2) 112m 9 кратно 3, поэтому 3x 12m 9, x 4m 3 .
Ответ: x 4m 3, y 3m 2 , где mZ .
2. Метод разложения на множители
Пример 3. Найти все целочисленные решения уравнения: x2 − 3xy + 2y2 =3.
Решение. Разложим левую часть уравнения x2 − 3xy + 2y2= 3 на множители:
X2 − 3xy + 2y2 = (x − y)(x − 2y). Имеем: (x − y)(x − 2y) = 3. Поскольку число 3 можно представить в виде произведения целых чисел с учетом порядка четырьмя способами: 3 = 1 · 3 = 3 · 1 = (−1) · (−3) = (−3) · (−1), то получаем совокупность четырех систем для нахождения значений переменных.
целочисленными решениями которых являются соответственно пары (−1; −2), (5; 2), (1; 2), (−5; -2)
Ответ: (−1; −2), (5; 2), (1; 2), (−5; −2).
Пример 4. (Петербургские математические олимпиады) Решите уравнение с двумя неизвестными x и y в целых числах: 10x2 + 11xy + 3y2 = 7.
Решение. Левую часть уравнения можно представить в виде произведения двух сомножителей (5x+3y) и (2x+y), которые могут принимать только целые значения −7, −1, 1, 7, которые приводят к следующим парам целых корней (−4; 9), (14; −21), (4; −9), (−14; 21).
Ответ: (−4; 9), (14; −21), (4; −9), (−14; 21)
Пример 5. Решите уравнение относительно x, y и z в натуральных числах:
(x − y + z)(x2 + y2 + z2 ) = 2005.
Решение. Представим правую часть уравнения 2005 через произведение простых делителей 2005 = 5 · 401, где 401 можно записать как сумму трёх натуральных квадратов 256, 144 и единицы, что подходит по первому множителю. Для полноты решения необходимо рассмотреть и другие варианты представления правой части как 2005 = 1 · 2005, которые не дают новых решений. Ответ: (16; 12; 1).
3. Метод решения уравнения с двумя переменными как квадратного относительно одной из переменных
Пример 6. Решить уравнение в целых числах:5x2 + 5y2 + 8xy + 2y − 2x + 2 = 0.
Решение. Рассмотрим уравнение как квадратное относительно x:
5x2 + (8y − 2)x + 5y2 + 2y + 2,
D = (8y −2)2 −4●5(5y2 + 2y + 2) = 64y2−32y + 4 −100y2 −40y −40 = −36(y2 + 2y + 1) = −36(y + 1)2 .
Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.
−36(y + 1)2 = 0.
Это возможно при y = −1, тогда x = 1.
Ответ: (1;-1)
Пример 7. Решить уравнение в целых числах: x2 − xy + y2 = x + y.
Решение. Преобразуем уравнение x2 − x(y + 1) + y2 − y = 0. Рассмотрим его как квадратное относительно x:
D = (y + 1)2 − 4(y2 − y) = −3y2 + 6y + 1 ≥ 0
3(y − 1)2 ≤ 4, (y − 1)2 ≤ 2. Проверка для y = 0; 1; 2 дает искомые решения.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
4. Метод, основанный на выделении полного квадрата
Пример 8. Найдите все целочисленные решения уравнения:x2 − 6xy + 13y2= 9.
Решение. Преобразуем левую часть уравнения, выделив полные квадраты,
X2 − 6xy + 13y2 = (x2 − 6xy + 9y2) + 4y2 = (x − 3y)2 + (2)2 = 29, значит (2y)2 ≤ 29. Получаем, что y может быть равен 0; ±1; ±2.
1. y = 0. (x − 0)2 = 29. Не имеет решений в целых числах.
2. y = −1. (x + 3)2 + 4 = 29
(x + 3)2 = 25, x + 3 = 5 или x + 3 = −5 x = 2 или x = −8.
3. y = 1. (x + 3)2 + 4 = 29, (x − 3)2 = 25, x − 3 = 5 или x − 3 = −5 x = 8 или x = −2.
4. y = −2. (x + 6)2 + 16 = 29, (x + 6)2 = 13. Нет решений в целых числах.
5. y = 2. (x − 6)2 + 16 = 29, (x − 6)2 = 13. Нет решений в целых числах.
Ответ: (2; −1); (−8; −1); (8; 1); (−2; 1).
5. Метод, основанный на выражении одной переменной через другую и выделении целой части дроби
Пример 9. Решить в целых числах уравнение: 3x + 2y = 7.
Решение. Переписав уравнение в виде 2(x + y) = 7 − x, заключаем, что 7 − x кратно 2, т. е. 7 − x = 2k, k ∈ Z. Значит, x = 7 − 2k, и из исходного уравнения находим y = 3k −7. Следовательно, все пары вида (7 − 2k; 3k − 7), k ∈ Z являются решениями исходного уравнения.
Ответ: (7 − 2k; 3k − 7), k ∈ Z.
Пример 10. Решить в целых числах уравнение 3y − 2x = 8.
Решение. Выразим x через y, получим: x = (3y−8)/2 ∈ Z ⇒ y = 2n, n ∈ Z. Тогда x = (6n−8)/2 = 3n − 4, n ∈ Z. Следовательно, все пары вида (3n − 4; 2n), n ∈ Z являются решениями исходного уравнения.
Ответ: (3n − 4; 2n), n ∈ Z.
6. Применение алгоритма Евклида
Решить уравнение 4 х + 7 у = 16
Найдем НОД чисел 4 и 7 по алгоритму Евклида : НОД(4,7) = 1
Выразим число 1 через коэффициенты а = 4 и b =7, используя теорему о линейном разложении НОД: НОД ( а, b ) = au + bv .
Получим: 1 = 4 ∙ 2 + 7 ∙ (-1) u = 2, v = -1
Частное решение уравнения: х0 = 2 ∙ 16 = 32, у0 = -1 ∙ 16 = -16
7. Метод рассмотрения остатков от деления
Решить в целых числах уравнение 3х – 4у = 1; 3 х = 4 у + 1
Левая часть уравнения делится на 3, значит и правая должна делиться на 3. При делении на 3 могут получиться остатки 0, 1, и 2. Рассмотрим 3 случая.
1)y = 3p
3 x = 4 ∙ 3p + 1 = 12 p + 1, не делится на 3
2)y = 3p + 1, 3 x = 4 ∙ (3p + 1) +1 = 12 p + 5, не делится на 3
3) y = 3p + 2, 3 x = 4 ∙ (3p + 2) +1 = 12 p + 9, кратно 3
3 x = 3 (4 p + 3)
x = 4 p + 3
Ответ: x = 4 p + 3; y = 3p + 2
Заключение
В ходе работы над проектом:
Узнала историю возникновения диофантовых уравнений и биографию Диофанта;
Познакомилась с некоторыми типами диофантовых уравнений и научилась методам их решения;
Была доказана гипотеза о том, что некоторые задачи из школьного курса можно решить при помощи диофантовых уравнений;
Были рассмотрены и разобраны примеры некоторых задач, которые легко решаются при помощи диофантовых уравнений;
Значительно упростила работу с ними, поскольку альтернативным методом их решения выступал метод подбора, достаточно трудоёмкий и нецелесообразный, в случаях если на решение задачи даётся не так много времени;
Работа над проектом не только повысила мои знания в области математики, но и показала новые методы решения задач, которые я могу применять на практике;
Изучение истории развития и изучения диофантовых уравнений расширило мой кругозор;
Самое интересное, что каждое уравнение требует особого подхода, поскольку нет универсального метода для решения диофантовых уравнений.
Моя работа над диофантовыми уравнениями продолжается, предстоит ещё многие методы изучить, научиться их применять, а продуктом работы будет небольшой сборник-самоучитель.
Список литературы
1. Башмакова И.Г. «Диофант и диофантовы уравнения», М.:Наука,1972г.
2. Математика в понятиях, определениях и терминах. Ч.1. Пособие для учителей. Под ред. Л.В.Сабинина. М., «Просвещение», 1978. -320 с. (Библиотека учителя математики.) На обороте тит.л.авт.: О.В.Мантуров, Ю.К.Солнцев, Ю.И.Сорокин, Н.Г.Федин.
3. Е.П. Гринько, А.Г. Головач. Учебно-методическое пособие. Методы решения диофантовых уравнений при подготовке школьников к олимпиадам. Брест БрГУ имени А.С. Пушкина, 2013
4. http://elib.sfu-kras.ru/bitstream/handle/2311/68579/caoaz.pdf?sequence=1
5. Абакумова, С. И. Диофантовы уравнения / С. И. Абакумова, А. Н. Гусева // Фундаментальные и прикладные исследования в современном мире. – 2014. – Т. 1, №6. – С. 133–137.







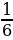 х+
х+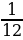 х+
х+ х+5+
х+5+ х+4=х решением данного уравнения будет число 84. Известным трудом Диофанта является «Арифметика», из которой до нас дошло лишь 6 из 13 книг, где он не только расписал методы решения 189 задач, но и придумал обозначения для неизвестных и некоторых математических знаков. Так же Диофант придумал такие приёмы решения уравнений, как: перенос неизвестных в одну сторону уравнения и приведение подобных членов. И, конечно, в его работах были приведены уравнения с двумя или более неизвестными, целыми коэффициентами и решением в целых числах.
х+4=х решением данного уравнения будет число 84. Известным трудом Диофанта является «Арифметика», из которой до нас дошло лишь 6 из 13 книг, где он не только расписал методы решения 189 задач, но и придумал обозначения для неизвестных и некоторых математических знаков. Так же Диофант придумал такие приёмы решения уравнений, как: перенос неизвестных в одну сторону уравнения и приведение подобных членов. И, конечно, в его работах были приведены уравнения с двумя или более неизвестными, целыми коэффициентами и решением в целых числах. Если стороны треугольника пропорциональны числам 3,4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения прямых углов на местности в древнем Египте: на веревке на равном расстоянии друг от друга завязывали узлы. В точке C, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали второй колышек в точке B(CB=4) и натягивали веревку так, чтобы AC=3,AB=5.Треугольник с такими длинами сторон называют египетским.
Если стороны треугольника пропорциональны числам 3,4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения прямых углов на местности в древнем Египте: на веревке на равном расстоянии друг от друга завязывали узлы. В точке C, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали второй колышек в точке B(CB=4) и натягивали веревку так, чтобы AC=3,AB=5.Треугольник с такими длинами сторон называют египетским.









