Линейные диофантовы уравнения

Линейные диофантовы уравнения

Исследовательская работа по алгебре

ученика 9 класса МОУ «Упшинская ООШ»

Антонова Юрия

«Если вы хотите научиться плавать, то

смело входите в воду, а если хотите

научиться решать задачи, то решайте их.»

Д.Пойя

Руководитель – Софронова Н.А .

Задача

Для настилки пола шириной в 3 метра имеются доски шириной в 11 см и 13 см. Сколько нужно взять досок того и другого размера?

Если х – число досок шириной в 11 см, а у – число досок шириной в 13 см, то нам надо решить уравнение:

11 х + 13 у = 300

Особенности уравнения 11 х + 13 у = 300: ▪ Коэффициенты 11, 13, 300 – целые числа. ▪ Число неизвестных превышает число уравнений. ▪ Решения данного уравнения х и у должны быть целыми положительными числам

Алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, в которых число неизвестных превышает число уравнений и для которых надо найти целые решения, называют неопределенными или диофантовыми, по имени греческого математика Диофанта .

Примеры диофантовых уравнений

1 . Найдите все пары целых чисел

x , y , для которых верно равенство

2 . Покажите, что уравнение

имеет бесконечное множество решений

целых числах

Цель работы:

Выяснить:

• Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Какие методы с уществуют для решения диофантовых уравнений?

Задачи:

• Найти и и зучить методы решения линейных диофантовых уравнений с двумя переменными.

• Рассмотреть возможности теории линейных диофантовых уравнений.

Пифагоровы тройки

• Неопределенные уравнения в целых числах решались еще до Диофанта. Большой интерес вызывало, например, алгебраическое уравнение x 2 + y 2 = z 2 , связывающее стороны x , у , z прямоугольного треугольника. Натуральные числа x , y и z , являющиеся решениями этого уравнения, называются "пифагоровыми тройками" .

Уравнение Ферма

• К работам Диофанта имеют непосредственное отношение и математические исследования французского математика Пьера Ферма. Считается, что именно с работ Ферма началась новая волна в развитии теории чисел. И одна из его задач - это знаменитое уравнение Ферма

х n + y n = z n

Ни один крупный математик не прошел мимо теории диофантовых уравнений.

Ферма, Эйлер, Лагранж, Гаусс, Чебышев оставили неизгладимый след в этой интересной теории.

1, ( Каталана); ах 2 + bxy + су 2 + dx + еу + f = 0 , где а , b , с , d , е , f — целые числа, т. е. общее неоднородное уравнение второй степени с двумя неизвестными (П.Ферма, Дж. Валлис, Л. Эйлер, Ж. Лагранж и К.Гаусс) " width="640"

Примеры неопределенных уравнений решаемых великими математиками 19-го и 20-го столетий: x 2 − ny 2 = 1 , где n не является точным квадратом (Ферма, Пелля); x z − y t = 1 , где z , t 1, ( Каталана); ах 2 + bxy + су 2 + dx + еу + f = 0 , где а , b , с , d , е , f — целые числа, т. е. общее неоднородное уравнение второй степени с двумя неизвестными (П.Ферма, Дж. Валлис, Л. Эйлер, Ж. Лагранж и К.Гаусс)

Диофантовы уравнения в 20 веке

1900 год. Международный математический конгресс.

10-я проблема Гильберта

Задано Диофантово уравнение с некоторым числом неизвестных и рациональными целыми коэффициентами. Необходимо придумать процедуру, которая могла определить за конечное число операций – является ли уравнение разрешимым в рациональных целых числах.

Русский математик Юрий Матиясевич доказал :

10-ая проблема Гильберта неразрешима - требуемого в ней алгоритма не существует.

Всегда ли можно найти для конкретного неопределенного уравнения все целые решения или доказать отсутствие таковых?

• Проблема решения уравнений в целых числах решена до конца только для уравнений первой степени с двумя или тремя неизвестными.
• ДУ второй степени с двумя неизвестными решаются уже с большим трудом.
• ДУ второй степени с числом неизвестных больше двух решены лишь в отдельных частных случаях, например уравнение x 2 + y 2 = z 2 .
• ДУ степени выше второй имеют, как правило, лишь конечное число решений (в целых числах).
• Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже задача существования целочисленных решений. Например, неизвестно, имеет ли уравнение

x 3 + y 3 + z 3 = 30 хотя бы одно целочисленное решение.

• Для решения отдельных ДУ, а иногда и для конкретных уравнений, приходится изобретать новые методы. Очевидно, что алгоритма, который позволял бы находить решения произвольных ДУ не существует.

Линейные диофантовы уравнения

Общий вид:

ЛДУ с двумя переменными:

a х + by = c

ЛДУ с тремя переменными:

a х + by + cz = d

ЛДУ с двумя неизвестными

ЛДУ с двумя переменными:

a х + by = c

Решения:

x = х 0 - bt

у = у 0 + at

Однородные:

a х + by = 0

Решения:

x = - bt

у = at

Поиск частного решения

Методы решения:

• Метод кратных.
• Применение алгоритма Евклида.
• Метод перебора.
• Метод спуска.

• Метод рассмотрения остатков от деления
• Метод рассмотрения остатков от деления

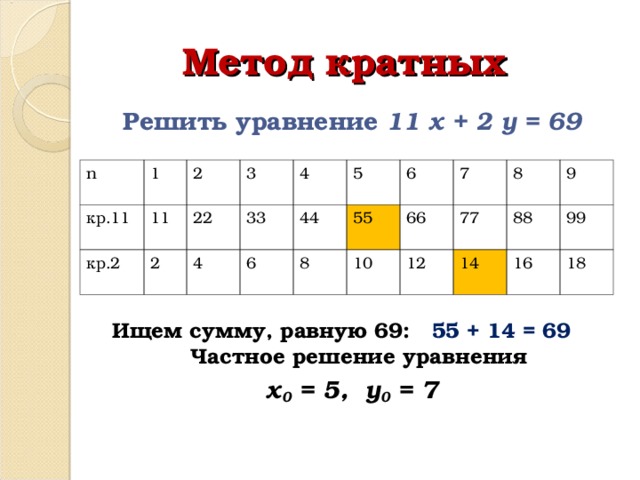
Метод кратных

Решить уравнение 11 х + 2 у = 69

Ищем сумму, равную 69: 55 + 14 = 69 Частное решение уравнения

х 0 = 5, у 0 = 7

n

кр.11

1

11

2

кр.2

3

2

22

33

4

4

5

44

6

55

6

8

10

7

66

77

12

8

14

9

88

99

16

18

Применение алгоритма Евклида

Решить уравнение 4 х + 7 у = 16

• Найдем НОД чисел 4 и 7 по алгоритму Евклида : НОД(4,7) = 1

• Выразим число 1 через коэффициенты а = 4 и b =7, используя теорему о линейном разложении НОД:

НОД ( а, b ) = au + bv .

• Получим: 1 = 4 ∙ 2 + 7 ∙ (-1) u = 2, v = -1

• Частное решение уравнения : х 0 = 2 ∙ 16 = 32,

у 0 = -1 ∙ 16 = -16

Метод перебора

Решить уравнение 7 х + 12 у = 100

• 7х + 12у = 100
• 7х = 100 – 12у
• 100 – 12у кратно 7

Частное решение уравнения : х 0 = 4, у 0 = 6

у

100-12у

0

х

0

1

2

88

3

76

64

4

5

52

6

40

7

28

16

4

8

4

Метод спуска: 3х+8у=60

Выразим

переменную х

через у

Выразим

переменную х

через t

Ответ:

Проверка:

Метод рассмотрения остатков от деления

• Решить в целых числах уравнение 3х – 4у = 1
• 3 х = 4 у + 1
• Левая часть уравнения делится на 3, значит и правая должна делиться на 3. При делении на 3 могут получиться остатки 0, 1, и 2.
• Рассмотрим 3 случая.

1

y = 3p

2

3 x = 4 ∙ 3p + 1 = 12 p + 1

3

y = 3p + 1

Не делится на 3

3 x = 4 ∙ (3p + 1) +1 = 12 p + 3

y = 3p + 2

Не делится на 3

3 x = 4 ∙ (3p + 2) +1 = 12 p + 9

3 x = 3 (4 p + 3)

x = 4 p + 3

Ответ:

Делится на 3

x = 4 p + 3 ; y = 3p + 2

Возможности теории ЛДУ Найти все целочисленные решения уравнения х 2 + 5y 2 + 34z 2 + 2ху - 10xz - 22уz =0

Что дала мне работа над проектом?

• Получил представление о работе над исследовательским проектом.
• Познакомился с историей развития диофантовых уравнений и биографией Диофанта.
• Изучил методы решения ЛДУ с двумя и тремя неизвестными.
• решил группу задач, которые носят практический характер, а также встречаются на олимпиадах, экзаменах за курс основной школы
• Приобрел навыки решения нестандартных задач.

Думаю, что в последующем я продолжу изучение диофантовых уравнений второй степени и методов их решения.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

• Математика в понятиях, определениях и терминах. Ч.1. Пособие для учителей. Под ред. Л.В.Сабинина. М., «Просвещение», 1978. -320 с. (Библиотека учителя математики.) На обороте тит.л.авт.: О.В.Мантуров, Ю.К.Солнцев, Ю.И.Сорокин, Н.Г.Федин.
• Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся. – 4-е изд., перераб. и доп. - М.: Просвещение, 1984. – 160с., ил.
• Н.П.Тучнин. Как задать вопрос? (О математическом творчестве школьников): Книга для учащихся. – М.: Просвещение, 1993. – 192с., ил.
• С.Н.Олехник, Ю.В.Нестеренко, М.К.Потапов Старинные занимательные задачи. –М.: Дрофа, 2002. -176с., ил.
• Я.И.Перельман. Занимательная алгебра. – М.: Наука, 1975г. – 200с., ил.
• Электорнный ресурс: http :// www.yugzone.ru /x/ diofant-i-diofantovy-uravneniya / И.Г.Башмакова «Диофант и диофантовы уравнения».
• Электорнный ресурс: http :// www.goldenmuseum.com /1612Hilbert_rus.html 10-я проблема Гильберта: история математического открытия (Диофант, Ферма, Гильберт, Джулия Робинзон, Николай Воробьев, Юрий Матиясевич).
• Электорнный ресурс: http://ru.wikipedia.org/wiki/ Диофантовы уравнения.
• Электорнный ресурс: http :// revolution.allbest.ru / mathematics /d00013924.html Белов Денис Владимирович Линейные диофантовы уравнения.
• Электорнный ресурс: http :// revolution.allbest.ru / mathematics /d00063111.html Линейные диофантовы уравнении
• Электорнный ресурс: http ://portfolio.1september.ru/work.php?id=570768 Зюрюкина Ольга. Неопределенные уравнения в целых числах или диофантовы уравнения.
• Электорнный ресурс: http ://portfolio.1september.ru/work.php?id=561773 Арапов Александр. Диофант и его уравнения.
• Электорнный ресурс: http :// ru.wikipedia.org / wiki / Алгоритм Евклида.