КЫРГЫЗ РЕСПУБЛИКАСЫНЫН БИЛИМ БЕРҮҮ ЖАНА ИЛИМ МИНИСТРЛИГИ
ЖАЛАЛ-АБАД МАМЛЕКЕТТИК УНИВЕРСИТЕТИ
ЖАЛАЛ-АБАД КОЛЛЕДЖИ
Табигый техникалык бөлүмү
Автоматташтырылган системалар жана математика
ЖАКтын окуу-усулдук “Бекитемин”
кеңешинде жактырылды
№ ___________ протоколу ЖАКтын директору
п.и.к., доцент Б.М.Турдубаева
______________К.Таштанова _________________________
“____” 2019-ж. “____” 2019-ж.
“Дискреттик математика жана сандык методдор” дисциплинасы боюнча
“Эсептөө техникасын жана автоматташтырылган
системаларды программалык камсыздоо” адистиги үчүн түзүлгөн
СИЛЛАБУС
Окутуучу: Полотова Алима Закировна
“Каралды”
Кесиптик билим берүүчү
ПЦКнын жыйынында жактырылды
№ ___________ протоколу
________________ Мусакулова Н.
(ПЦК башчысынын колу)
Жалал-Абад - 2019
Дисциплинанын аталышы: Дискреттик математика жана сандык методдор
Окутуучу: Полотова Алима Закировна
Мобилдик телефону: 0777-39-63-04
Электрондук дареги: [email protected]
Адистиги: 230109 “Эсептөө техникасын жана автоматташтырылган
системаларды программалык камсыздоо”
Курсу: 2 Семестри: 3 Кредити: 5
Окуу планы боюнча жалпы сааттын саны: 150 саат.
лекциянын саны: 36
практикалык сабактын саны: 54
студенттин Ө.А.И. саны: 60
модулдун саны: 2
жыйынтыгы: экзамен
Өз алдынча ишти жана отработканы кабыл алуу графиги:
| Курс | Тайпа | Жуманын күнү | Убактысы | Кабинеттин номери |
| 2 | ПОВТАСк-01-19 | Шейшемби, Жума | 1030-1130 | 302 |
Студенттердин милдеттери:
ЖАМУдагы модулдук-рейтинг системасынын шарттары менен таанышат;
Сабактарды, модулдарды, жыйынтыктоочу текшерүүлөрдү себепсиз үзгүлтүккө учуратпайт;
Өз убагында рейтинг баракчалары менен таанышат;
Учурдагы текшерүүнү, аралыктагы текшерүүнү, өз алдынча иштерин өз учурунда тапшырат;
Эгерде тапшыра албай калса тастыктоочу тактаманы көрсөтөт.
Студенттерге коюлган талаптар:
Сабакты себепсиз калтырбоо;
Сабактарга өз убагында катышуу;
Сабактарда өзүн тартиптүү алып отуруу;
Эгерде сабакка келбесе, ошол күнкү сабактын конспектиси текшерилет жана 2 же 3 суроолорго жооп берүүсү талап кылынат;
Сабакка келип катышуу гана эмес, жекече, жупта жана топтордо иштөөсүн, өз оюн тартынбай айтуусун, курстун мазмунун үйрөнүүгө багытталган билим жөндөмдүүлүгүн, активдүүлүгүн көрсөтүү;
Күн сайын окуп-үйрөнүү ишмердүүлүгүн, билгичтик көндүмдөрун арттыруу жана жогорулатуу;
Берилген үй тапшырмасын так жана туура аткаруу менен балл топтоо;
Лекциялык сабактарда берилген өз алдынча иштерди тиешелүү формага жараша, өз убагында тапшыруу жана дептерге өз кол жазмасы менен жазуу, коргоо.
Жогорудагы талаптардын иш жүзүнө ашырылышы менен ар бир студенттин жөндөмдүүлүктөрү, предметти канчалык деңгээлде билүүсү, тапкычтыгы, чыгармачылыктары, изденүүчүлүктөрү, ар тараптуулуктары, байкагычтыктары чагылдырылат.
Академиялык чынчылдыктын принциптеринин сакталышы:
Студенттер өз алдынча иштерди кол жазма менен жазуусу керек;
Өз алдынча иштерди көрсөтүлгөн формада, б.а. жазуу жүзүндө, кластер, доклад, таблица түрүндө тапшыруусу керек;
Интернеттен көчүрүп алган өз алдынча иштер жарабайт;
Жазган иштерин коргоолору керек;
Ар бир тема үчүн план жазылуусу керек.
Лекциянын темалары, сааты:
| № | Лекциянын темалары | Сааты |
| 1. | Көптүктөр жөнүңдө түшүнүк | 2 |
| 2. | Көптүктөрдүн үстүнөн жүргүзүлүүчү амалдар | 2 |
| 3. | Бинардык катыш | 2 |
| 4. | Айтылыштар жана алардын үстүнөн жүргүзүлүүчү операциялар | 2 |
| 5. | Эсептөө системалары | 2 |
| 6. | Математикалык индукция | 2 |
| 7. | Комбинаториканын элементтери | 2 |
| 8. | Графтын негизги түшүнүктөрү | 2 |
| 9. | Графтардын үстүнөн жүргүзүлүүчү операциялар | 2 |
| 10. | Коддоо теориясынын элементтери | 2 |
| 11. | Жакындатылган сандар | 2 |
| 12. | Сызыктуу эмес теңдемелер | 2 |
| 13. | Алгебралык теңдемелерди чыгаруу методдору | 2 |
| 14. | Сызыктуу теңдемелер системасы. Гаусстун методу | 2 |
| 15. | Сызыктуу теңдемелер системасын жакындаштырып чыгаруунун методдору | 2 |
| 16. | Сандык интегралдоо методдору | 2 |
| 17. | Дифференциалдык тендемелерди чыгаруу | 2 |
| 18. | Чыгаруунун методдору | 2 |
|
| Жалпы: | 36 |
Практикалык сабактын темалары, сааты:
| № | Практикалык сабактын темалары | Сааты |
| 1. | Көптүктөрдүн үстүнөн жүргүзүлүүчү амалдар | 2 |
| 2. | Көптүктөрдүн декарттык көбөйтүндүсү | 2 |
| 3. | Бинардык катыш | 2 |
| 4. | Айтылыштар жана алардын үстүнөн жүргүзүлүүчү операциялар | 2 |
| 5. | Эсептөө системалары | 2 |
| 6. | Математикалык индукция | 2 |
| 7. | Комбинаториканын элементтери | 2 |
| 8. | Графтын негизги түшүнүктөрү | 2 |
| 9. | Графтын элементтери | 2 |
| 10. | Графтардын үстүнөн жүргүзүлүүчү операциялар | 2 |
| 11. | Алгоритм түзүү | 2 |
| 12. | Коддоо теориясынын элементтери | 2 |
| 13. | Автоматтар теориясынын элементтери | 2 |
| 14. | Жакындатылган сандар | 2 |
| 15. | Сызыктуу эмес теңдемелер | 2 |
| 16. | Алгебралык теңдемелерди чыгаруу методдору | 2 |
| 17. | Сызыктуу теңдемелер | 2 |
| 18. | Аныктагычтар | 2 |
| 19. | Тескери матрица | 2 |
| 20. | Крамердин эрежеси | 2 |
| 21. | Гаусстун методу | 2 |
| 22. | Сандык интегралдоо методдору | 2 |
| 23. | Симпсондун формуласы | 2 |
| 24. | Дифференциалдык тендемелерди чыгаруу. Эйлердин методу | 2 |
| 25. | Эйлердин жакшыртылган методу | 2 |
| 26. | Рунге-Куттанын методу | 2 |
| 27. | Адамстын методу | 2 |
|
| Жалпы: | 54 |
Өз алдынча иштин темалары, сааты
| № | Өз алдынча иштин темалары | сааты |
| 1. | Эйлер-Венндин диограммасынын келип чыгышы | 2 |
| 2. | Көптүктөрдүн үстүнөн жүргүзүлүүчү амалдардын ар бирине 5тен мисал келтирүү | 2 |
| 3. | Кортеждер, алардын түрлөрү | 2 |
| 4. | Чагылтуу түшүнүгүнө 5 мисал келтирүү | 2 |
| 5. | Предикаттар жана алардын түрлөрү | 2 |
| 6. | Эсептөө системасынын келип чыгышы | 2 |
| 7. | Математикалык индукция методун колдонуп 3мисал чыгаруу | 2 |
| 8. | Дедукция жана индукция методдорун салыштыруу | 2 |
| 9. | Бульдун функциялары | 2 |
| 10. | Алгоритм жөнүндө түшүнүк | 2 |
| 11. | Графтын келип чыгуу тарыхы | 2 |
| 12. | Графтын атайын түлөрү | 2 |
| 13. | Графтын матрицасы | 2 |
| 14. | Графтын колдонулуштары | 2 |
| 15. | Автоматтар теориясынын элементтери | 2 |
| 16. | Эсептөө каталыктары | 2 |
| 17. | Каталыктарды азайтуу методдору | 2 |
| 18. | Тамырларды ажыратуунун алгоритми | 2 |
| 19. | Хордалар методу | 2 |
| 20. | Кесиндини тең экиге бөлүүнүн алгоритми | 2 |
| 21. | Ньютондун методу | 2 |
| 22. | Итерация методу | 2 |
| 23. | Матрица жана анын үстүнөн жүргүзүлүүчү амалдар | 2 |
| 24. | Гаусстун методунун алгоритми | 2 |
| 25. | Сызыктуу алгебранын башка маселелери | 2 |
| 26. | Сандык интегралдоо алгоритмдери | 2 |
| 27. | Өздүк эмес интегралдарды жакындатып эсептөө | 2 |
| 28. | Пикардын методу | 2 |
| 29. | Прогонка методу | 2 |
| 30. | Кадимки дифференциалдык бир теңдемени бардык методдорду колдонуп чыгаруу | 2 |
|
| Жалпы: | 60 |
1-модул
| № | Өз алдынча иштин тапшырмалары | Балл | Текшерүүнүн түрү |
| 1. | Эйлер-Венндин диограммасынын келип чыгышы. | 3 балл | Конспект жазуу |
| 2. | Көптүктөрдү класстарга ажыратуу. | 3 балл | Таблица түзүү |
| 3. | Көптүктөрдүн үстүнөн жүргүзүлүүчү амалдардын ар бирине 5тен мисал келтирүү. | 3 балл | Мисал иштөө |
| 4. | Бульдун алгебрасы жана функциясы. | 4 балл | Доклад жазуу |
| 5. | Дарак, анын касиеттери жана колдонулуштары. | 4 балл | Презентация |
| 6. | Адамдын мүмкүнчүлүгү менен автоматтын салыштырмалуу анализи | 3 балл | Доклад |
|
| Жалпы: | 20 балл |
|
2-модул
| № | Өз алдынча иштин тапшырмалары | Балл | Текшерүүнүн түрү |
| 1. | Кесиндини тең экиге бөлүү | 3 балл | Алгоритм түзүү |
| 2. | Ньютондун методу | 3 балл | Конспект жазуу |
| 3. | Итерация методу | 3 балл | Синквейн түзүү |
| 4. | Анык интегралды сандык эсептөөнүн методдору | 3 балл | Таблица түзүү |
| 5. | Өздүк эмес интегралдарды жакындаштырып эсептөө | 4 балл | Доклад жазуу |
| 6. | Кадимки дифференциалдык теңдемени бардык методдорду колдонуп чыгаруу | 4 балл | Мисал иштөө |
|
| Жалпы: | 20 балл |
|
Модулду кабыл алуу шарты:
Бир модул учурдагы текшерүүдөн (УТ) 10 балл + аралык текшерүүдөн (АТ) 30 балл + студенттин өз алдынча ишинен (СӨАИ) 20 балл турат, б.а. 10+30+20=60 балл.
критерийлер жана көнүмдөргө ылайык студенттердин тапшырмаларды аткаруусу, өтүлгөн материалдарды өздөштүрүүсү, сабактардагы катышуусун, жетишүүсүн эске алуу менен 0-10 го чейинки балл менен бааланып, окутуучу тарабынан модул башталганга чейин коюлат.
Учурдагы текшерүү (УТ) бааланбаса (же окутуучу тарабынан 0 балл коюлса) студент текшерүүго (окутуучу тарабынан) киргизилбейт. Модулдагы учурдагы текшерүүдөгү “0” балл коюлат, эгер студент ошол предметке бир жолу да катышпаса жана предметтен эч кандай баа албаса.
Учурдагы текшерүүнүн 10 баллынын 5 баллы студенттердин сабактарга катышуусуна берилет, активдүүлүгүно да 5 балл берилет.
Студент модул тапшыруу учурунда модул алуучу окутуучунун кабары жок модулдун графигинен башка убакытта, башка жайда тапшырып балл алган учурда, предмет боюнча модул алган окутуучу тарабынан бул жагдай жөнүндо факультеттин деканы (колледждин директору) тарабынан тастыкталып, баллды жокко чыгаруу жөнүндө билдирүүсү менен окуу бөлүмүнө кайрылат.
Аралык текшерүү (АТ): 0-30 балл(тесттеги суроолордон алган баллы).
Студенттердин өз алдынча иштери (СӨАИ): 0-20 балл (тесттик суроолордон алган баллы).
Модулдарды (экзамендерди) тапшыруу компьютердик тестирлөө аркылуу жүргүзүлөт.
Бул учурда аралыктагы текшерүү (АТ) жана студенттердин өз алдынча иштери (СӨАИ) бириктирилип, окуу процессинин графигине ылайык жүргүзүлүп, 0-50 баллга чейин бааланат, ага учурдагы текшерүүнүн (УТ) 10 баллы кошулат.
Студенттин модулдагы арифметикалык орточо баллы 31-60 болсо, ал жыйынтыктоочу текшерүүго киргизилип, экзамен учурунда билимине жараша 0-40 балл ала алат.
Студенттин жалпы блоктогу арифметикалык орточо баллы 0-30 болсо, ал жыйынтыктоочу текшерүүго киргизилбейт, жайкы семестрге калтырылат.
Сабактардын жыйынтык баллы (экзамен) сынак китепчеге жана экзамендик ведомостко төмөндөгү шкала менен коюлат:
61-73 балл - “канааттандыраарлык” “3”,
74-86 балл - “жакшы” “4”,
87-100балл - “эң жакшы” “5”.
Учурдагы текшерүүнүн (модулдун) жогорулатуу үчүн кайрадан тапшырууга уруксат берилбейт. Учурдагы текшерүүго келбеген (киргизилбеген) студентке “кж” белгиси коюлат.
Студенттин биринчи модулга кандайдыр бир жүйөлүү себептер менен келбей калса (киргизилбесе) тастыктоочу документтердин негизинде, кийинки модулга эки жума калганда факультеттин деканы тарабынан уруксат берилет жана кафедра тарабынан модулду тапшырууга жекече график түзүлөт, ал эми модулга себепсиз келбей калса:
деканат тарабынан сабакка катышуусу анализденип, окуудан чыгарууга сунушталат;
ушул Жобонун 4,9, пунктунун негизинде жыйынтыктоочу текшерүүгө киргизилбейт.
Экинчи модулга же жыйынтыктоочу текшерүүгө кандайдыр бир жүйөлүү себептер менен
келбей калган студенттерге модулдарды тапшырууга уруксат тастыктоочу документтердин негизинде “Окуу процессин окутуунун кредиттик технологияларынын (ECTS) негизинде уюштуруу” жөнүндө жобого ылайык сессиядан кийин академиялык карыздарды жоюу мезгилинде берилет.
Экинчи курстар үчүн “Жайкы семестрдин” жобосуна ылайык, жайкы семестр уюштурулат.
Модулдук (экзамендик) тесттер
Көптүктөрдү түзгөн жаратылыштагы ар кандай обьектилер эмне деп аталат?
Көптүктөн элементи
Көптүктүн символу
Көптүктөн алфавити
Көптүктүн системасы
Практикада көптүктөр негизинен канча түрдүү жол менен берилет?,
2
4
1
Берилбейт
Бош көптүк деген эмне?
Элементи 1өө болсо
Эч кандай элементи жок болсо
Элементтери аз болсо
Көптүктөгү элементтери 5өө болсо
Натуралдык сандардын көптүгү кандай белгиленет?
R тамга
Z тамга
А тамга
N тамга
A={1,3,5,6,7,9} жана B={1,2,3,4,5,6,7} көптүктөрүнүн кесилишин тап.
A∩В={1,3,5,6,7}
A∩В={1,3,5,6,7,9}
A∩В={1,3,4,5,6,7,9}
A∪В={a,c,d.e}
А={ a,b,c,d,e,f} жана B={b,f,k,L} көптүктөрүнүн биригүүсүн тапкыла?
A∪B={a,c,d,e}
A∪B={a,b,c,d,e,f,k,l}
A∪B={f,b}
A∪B={1,3,4,5,6}
Айтылыш деген эмне?
Далилдөөсүз кабыл алынган сүйлөм
Далилдөөнү талап кылуучу сүйлөм
Чын же жалган экендигин айтууга мүмкүн болгон сүйлөм
Белгисизди кармап турган сүйлөм.
«Коньюнкция » сөзү биздин тилде кандай маанини түшүндүрөт?
«Бириктирем»
«Айырмалайм»
«Бөлүп көрсөтөм»
«Тыгыз байланыштырам»
«Дизьюнкция » сөзү биздин тилде кандай маанини түшүндүрөт?
«Бөлүп көрсөтөм»
«Айырмалайм»
«Бириктирем»
«Тыгыз байланыштырам»
«Импликация » сөзү биздин тилде кандай маанини түшүндүрөт?
«Тыгыз байланыштырам»
«Бириктирем»
«Айырмалайм»
«Бөлүп көрсөтөм»
Натуралдык сандардын көптүгүнө тиешелүү болгон сандарды көрсөткүлө?
1,2,3,4,5,6
0,1,-3,4,5,-6
7,-9,10
-2,-1,0,1,2
Эч кандай элементи жок көптүк … көптүк деп аталат?
Барабар
Бош
Камтылган
Чектүү
Көптүк түшүнүгунүн негизинде кандай фигураны аныктоого болот?
Эйлер-Венндин диограммасын
Бош
Алгебралык
Геометриялык
Белгисизди кармап турган айтылыш эмне деп аталат?
Тавталогия
Теорема
Предикат
Квантор
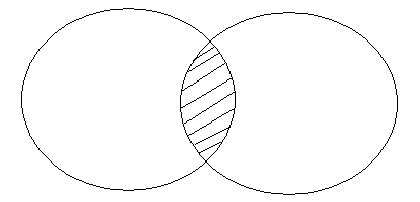
Бул диаграмма кайсы көптүккө таандык?
Кесилишүүсү
Толуктоочу
Айырмасы
Биригүүсү
Чын же жалган экендигин айтууга мүмкүн болгон ар кандай жай сүйлөм ... деп аталат.
Граф
Теорема
Картеж
Айтылыш
Чын айтылышты тапкыла?
Бүгүн жуманын кайсы күнү?
Бермет 5-класста окуйт.
27 саны 5 ке бөлунөбү?
Жашасын элдердин достугу!
Төмөндөгү айтылыштардан жалган болгон айтылышты көрсөт?
9 натуралдык сан
Бүгүн жаан жаайт
5 саны 2ге бөлүнөт
11 так сан
Бүтүн сандардын көптүгүнө тиешелүү болгон сандарды көрсөткүлө?
1,-3,4,5,-6
3,5,6,7,2.1
√2, 7,-9,10
5 э Q
А= {a,f,h,t,e,k} көптүгүнө камтылган көптүктү тапкыла.
В={s,f,h,e,a}
C={a,f,h,t,e,k,ж}
С={a,f,t,e,k}
А∪В={a,c,d,e}
А= {2,4,6,8,10,12,14} көптүгүнө камтылган көптүктү тапкыла?
В={s,f,h,e,a}
C={2,4,3,5}
A={-1,0,2,4,6,8}
A={4,6,8,12}
Төмөндөгү сүйлөмдөрдүн кайсы бири айтылыш экендигин аныктагыла?
Сегиз бүтүн сан.
Жашасын Кыргызстан!
Силер математиканы жакшы көрөсунөрбү?
Бүгүн кандай көңүлдүү күн.
Төмөндөгү айтылыштардан жалган айтылышты көрсөткүлө?
13 так сан
7 жуп сан
2/3 рационалдык сан
5 натуралдык сан
А={2,3,4,6,7} жана В={0,1,8,5,6,7} көптүктөрү берилсе, А\В айырмасын тапкыла?
А\В={2,3,4}
А\В={6,7}
А∩В={0,20,3,5,8}
В\А={0,1,8,5}
Көптүктөрдү сүрөттөө математикага ким тарабынан киргизилген?
Ренне Декарт
Джон
Эйлер-Венн
Де Морган
«4 саны (х+2):3=18 тендемесинин тамыры болот» айтылышы чын же жалган экендигин аныктагыла.
чын айтылыш
жалган айтылыш
билбейм
айтылыштын тануусу
Белгисизди кармап турган айтылыш эмне деп аталат?
квантор
предикат
теорема
аксиома
7 санын экилик эсептөө системасындагы көрүнүшүн көртсөт?
111(2)
101(2)
11110(2)
1101(2)
Ондук эсептөө системасында эң кичине жана эн чоң эки орундуу сандарды көрсөт.
10 жана 99
11 жана 100
10 жана 90
01 жана 99
Үчтүк эсептөө системасы кайсыл цифралардан турат?
1, 2, 3
0, 1, 2
1, 2
-1, 0, 1, 2
Орто суроолор (30 суроо)
Көптүктөрдүн санын саноого мүмкүн эмес болсо, анда . . . көптүк деп аталат.
Чексиз
Барабар
Чектүү
Бош
Көптүктүн элементтерин санап чыгууга же номерлөөгө мүмкүн болсо, анда ал . . . көптүк болот.
Чектүү
Барабар
Камтылган
Бош
Көптүктүн белгилениши кандай?
g,α,β,...
А,B,С,D,...
a,b,c,...
А,Б,В,Г,...
Бирдей элементтерден турган көптүктөр эмне деп аталат?
Барабар көптүктөр
Чектүү көптүктөр
Барабар эмес көптүктөр
Чексиз көтүктөр
«24 саны жуп жана 2 ге бөлүнөт» айтылышында айтылыштардын кандай операциясы жүргүзүлгөн?
Коньюнкция
Дизьюнкция
Импликация
Эквиваленция
"7≥5" айтылышында айтылыштардын кандай операциясы жүргүзүлгөн?
Дизъюнкция
Импликация
Эквиваленция
Конъюнкция
«24 саны жуп болсо, анда ал 2 ге бөлүнөт» айтылышында айтылыштардын кандай операциясы жүргүзүлгөн?
Конъюнкция
Импликация
Дизъюнкция
Эквиваленция
«4 саны (х+2):3=18 тендемесинин тамыры болот» айтылышы чын же жалган экендигин аныктагыла.
Чын
Жалган
Билбейм
Жалганда эмес, чын да эмес
Х ={1,2,3} жана У = { a,d,f} көптүктөрүнүн декарттык көбөйтүндүсүн тапкыла?
X×Y={(1,a),(1,d),(1,f),(2,a),(2,d),(2,f),(3,a),(3,d),(3,f) }
X×Y={1,2,3,a,d,f}
X×Y={∅}
X×Y={1,2,}
«4 саны x+14=18 тендемесинин тамыры болот» айтылышы чын же жалган экендигин аныктагыла?
Чын
Жалган
Жалганда эмес, чын да эмес
Билбейм
А={ a,b,c,d,e,f} жана B={b,f,k,L} көптүктөрүнүн биригүүсүн тапкыла?
A\B = {a,f,k,L}
A\B = {a,c,d,e}
A\B = {a,c,d}
A∪B={a,b,c,d,e,f,r,l}
А={2,3,4,6,7} жана В={0,1,8,5,6,7} көптүктөрү берилсе, А∩В кесилишүүсүн тапкыла?
А\В={2,3,4}
А∩В={6,7}
В∩А={0,1,8,5}
А∩В={0,20,3,5,8}
Айтылыштадын экөө тең жалган болгондо гана жалган, калган учурлардын бардыгында чын болгон курама айтылыш, ал айтылыштардын ... деп аталат.
Конъюнкциясы
Дизъюнкциясы
Тануусу
Эквиваленциясы
Айтылыштар түзүлүшү боюнча кандай болуп бөлүнүшөт?
Бир жана көп орундуу
Барабар, барбар эмес
Татаал, жөнөкөй
Жөнөкөй, курама
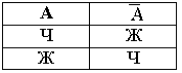
Бул ... чындык маанилеринин таблицасы?
Көптүктүн
Тануунун
Конъюнкциянын
Комбинаториканын
Айтылыштардын тануусунун тануусу кандай аталат?
Чектүү тануу
Барабар тануу
Бош тануу
Кош тануу
А = {3,7,9,4} жана В = {9,4,7,3} кайсы көптүккө мисал боло алат?
Толуктоочу
Барабар
Бош
Камтылган
Көптүктүн элементтери кандай белгиленет?
Латын алфавитинин кичине тамгасы менен a,b,c,d…
Латын алфавитинин чон тамгасы менен A,B,C,D…
α,β,g
А,Б,В,Г,... тамгалары менен
Көптүктөрдүн түрлөрү?
Анык, анык эмес, бош
Мезгилдүү, мезгилсиз, бош
Чектүү, чексиз, бош
Жөнөкөй, татаал, бош
Көптүктөрдүн айырмасынын символикалык белгилениши кандай?
А∩ В= В∩ А
A\B=X (X∈A жана X∋B)
А ∨В= А∧ В
А\ В=А\ (АUВ)
Ондук эсептөө системасында эң кичине жана эн чоң эки орундуу сандарды көрсөт.
20 жана 56
10 жана 98
09 жана 99
10 жана 99
Факториал (!) тушүнүгү эмнени билдирет?
Берилген сандардын суммасын
Берилген сандардын айырмасын
Берилген сандардын тийиндисин
1ден n ге чейинки сандардын көбөйтүндүсүн
5! канчага барабар?
5
10
100
120
Чоку деп аталган чекиттер менен бул чекиттерди туташтырган кабырга деп аталган чиймелердин жыйындысы . . . деп аталат?
Граф
Кабырга
Орграф
График
Графтын чокуларын туташтырып турган сызык . . . деп аталат?
Граф
Кабырга
Орграф
Чоку
Рим эсептөө системасында 1000 санынын белгилениши?
М
C
D
T
Төмөндөгү айтылыштардан жалган айтылышты көрсөткүлө?
6 жуп сан
13 так сан
11 жөнөкөй сан
21 терс сан
��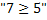
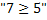 айтылышында айтылыштардын кандай операциясы жүргүзүлгөн?
айтылышында айтылыштардын кандай операциясы жүргүзүлгөн?
Дизъюнкция
Импликация
Конъюнкция
Эквиваленция
199 санын римдик эсептөө системасында жазгыла?
CXCIX
CLXXXXIX
MVXC
CMXIX
LXVIII санын ондук эсептөө системасында жазгыла?
68
568
5153
653
Татаал суроолор (30 суроо)
Математикадагы чектүү көптүктөрдүн касиеттерин изилдөөчү бөлүмдөрдүн жалпы аты . . . деп аталат?
Дискреттик математика
Алгебра
Геометрия
Анализ
Жалгыз кабырганы аныктап турган чокулар . . . деп аталат?
Жанаша кабыргалар
Изоляцияланган чоку
Жанаша чокулар
Нөл граф
Эгерде граф жалаң гана изоляцияланган чокулардан турса, анда ал ... деп аталат.
Жанаша кабыргалар
Изоляцияланган чоку
Жанаша чокулар
Нөл граф
Бир чокудан чыгып жана ошол чокуга кирген кабырга . . . деп аталат?
Багытталган
Аралаш граф
Жаа
Сыйыртмак
Кабыргалардын арасында жаалар менен катар багыты жок кабыргалар берилсе . . . деп аталат?
Багытталган
Жаа
Аралаш граф
Сыйыртмак
Эч бир кабыргасынын багытты көрсөтүлбөгөн граф . . . деп аталат?
Толук багытталган
Багытталбаган граф
Мультиграф
Байланган граф
Даракка кирген кабыргалар анын . . . деп аталат?
Дарак
Бутактары
Дарактын хордасы
Байланышпаган токой
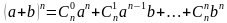 формуласы . . . деп аталат?
формуласы . . . деп аталат?
Ньютондун биному
Бернуллинин формуласы
Де Моргандын формуласы
Эйлер-Венндин диаграммасы
Эмненин сүрөттөлүшү көрсөтүлгөн?
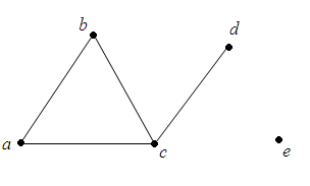
Граф
График
Үч бурчтук
Ромб
Эгерде кабыргалар жалгыз чокуга ээ болсо, анда эки кабырга . . . деп аталат?
Жанаша кабыргалар
Изоляцияланган чоку
Жанаша чокулар
Нөл граф
Эгерде графтын чокуларынын жайланыш багыты мурдатан көрсөтүлгөн болсо, анда ал . . . граф деп аталат?
Багытталган
Жаа
Аралаш граф
Сыйыртмак
3215 санынын разряддык кошулуучулардын суммасы түрүндө берилишин көрсөт?
3215=3∙102+2∙10+1+50
3215=5∙103+1∙102+2∙10+3.
3215=3∙103+2∙102+1∙10+5
3215=3000+200+15
Кандайдыр бир иш-аракеттерди программасын алгоритм деп атоо үчүн талаптарды канаттандыруу керек. Ал талаптарды эмне деп аталат?
Алгоритмдин усулдары
Алгоритмдин белгилери
Алгоритмдин берилиши
Алгоритмдин касиеттери
Индукция методу . . . келтирүү болуп саналат?
Жекеликтен -жалпылыкка
Логикалык ой жүгүртүүгө
Жалпылыктан- жекеликке
Негизги теоремага
3!+4! канчага барабар?
30
1442
7
122
 канчага барабар?
канчага барабар?
100
1
0
99
 туюнтмасынын маанисин эсептегиле.
туюнтмасынын маанисин эсептегиле.
1440
24
100
720
Эки адам сүрөттөрүн алмаштырышты, баары канча сүрөт болгон?
2
3
4
1
Эгерде графтын чокусу эч кандай кабыргага инциденттүү болбосо, анда ал . . . деп аталат?
Жанаша кабыргалар
Изоляцияланган чоку
Жанаша чокулар
Нөл граф
Эгерде каалагандай эки чокусу жок дегенде бир багытка ээ болсо, анда . . . деп аталат?
Толук багытталган
Багытталбаган граф
Мультиграф
Байланган граф
“∀” символу кайсыл сөздүн синоними катары колдонулат?
“Каалагандай”
“Жашайт”
“Жана”
“Бирөө гана”
Аткаруучунун тилинде жазылган алгоритм . . . деп аталат?
Бейсик
Программа
Башкаруу
Термин
Алгоритмдин негизиги канча касиети бар?
6
5
4
7
Орундаштыруунун формуласын тапкыла?
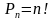
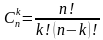
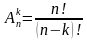
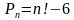
Орун алмаштыруунун формуласын тапкыла?
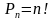
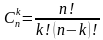
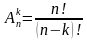
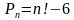
32 санынын экилик эсептөө системасындагы көрүнүшүн жазгыла?
1000002
322
22222
100112
Кандайдыр бир иш-аракеттерди программасын алгоритм деп атоо үчүн талаптарды канаттандыруу керек. Ал талаптарды эмне деп аталат?
Алгоритмдин усулдары
Алгоритмдин белгилери
Алгоритмдин берилиши
Алгоритмдин касиеттери
Топтоштуруунун формуласын тапкыла?
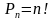
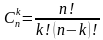
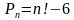
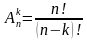
5!+3! канчага барабар?
126
122
100
8!
5!-4! канчага барабар?
96
69
421
1!
Өз алдынча ишттин суроолору (75 суроо)
«Предикат» деген эмне?
Далилденүүчү сүйлөм
Белгисизди кармап турган айтылыш
Далилдөөсүз кабыл алынган сүйлөм
Айырманы билдирүчү сүйлөм
Картеж сөзүнүн мааниси кандай?
Түгөй
Предикат
Парад же салтанаттуу жүрүш
Иреттүү сандар
Эки же андан ашык белгисиздери камтыган предикаттар кандай предикаттар деп аталат?
Бош орундуу
Көп орундуу
Бир орундуу
Чексиз орундуу
Берилген даракка кошумча болуп кирген кабыргадан түзүлгөн граф дарактын . . . деп аталат?
Дарак
Дарактын хордасы
Байланышпаган токой
Дарактын бутактары
57 санын экилик эсептөө системасындагы көрүнүшүн көртсөт?
1110012
1100012
2001113
40101015
Топтоштуруунун формуласын тапкыла?
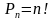
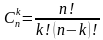
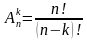
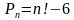
2!6! канчага барабар?
1440
8
124
1225
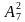 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?
42
12
7
56
 туюнтмасынын маанисин эсептегиле.
туюнтмасынын маанисин эсептегиле.
15
42
24
440
Жарышка 10 адам катышкан, канча жол менен орундарды бөлүштүрүүгө болот.
3628800
234534
43676866
45464546
Эгерде графтын каалагандай эки чокусу 2 же андан көп кабыргалар же жаалар менен бириктирилсе, ал граф . . . деп аталат?
Толук багытталган
Багытталбаган граф
Мультиграф
Байланган граф
Графтын бардык чокуларынын арасында эң аз дегенде бир жол болсо, анда бул граф
. . . деп аталат?
Толук багытталган
Багытталбаган граф
Мультиграф
Байланган граф
Графтын кандайдыр бир эки чокусунун арасында жол жок болсо,анда бул граф
. . . деп аталат?
Байланбаган граф
Багытталбаган граф
Байланган граф
Мультиграф
Жок дегенде 2 чокудан туруп циклдерди кармабаган чектүү байланышкан графты
. . . деп айтабыз?
Дарак
Дарактын бутактары
Дарактын хордасы
Байланышпаган токой
 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?
6
2
9
4
 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?
100
4
9
24
Кванторлордун канча түрү бар?
Чектүү
2
Чексиз
Жок
Ар бир байланыш компоненти кайрадан дарак болгон байланышпаган граф . . . деп аталат?
Дарак
Дарактын хордасы
Дарактын бутактары
Токой
Бул диаграмма көптүктөдүн кайсыл амалына таандык?
Биригүү
Кесилишүү
Айырма
Толуктоосу
Бул диаграмма көптүктөрдүн кайсыл амалына таандык?
Биригүү
Кесилишүү
Айырма
Толуктоосу
Кабыргалардын арасында жаалар менен катар багыты жок кабыргалар берилсе . . . деп аталат?
Багытталган
Жаа
Аралаш граф
Сыйыртмак
Блок-схемадагы “ромб” геометриялык фигура кандай команданы тушүндурөт?
Блок-схеманын башын
Кандайдыр бир шарттарды текшерүүчү команда
Кандайдыр бир шартты сөзсүз аткаруу керектигин
Блок-схеманын аягын
Алгоритмдин башталышын жана аягын кандай геометриялык фигура сурөттөйт.
Тик бурчтук
Ромб
Элиппс(овал)
Стрелкалар
 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?
100
2540
99
1440
“∨” символу кайсыл сөздүн синоними катары колдонулат?
“Каалагандай”
“Жашайт”
“Жана”
“Же”
"" символу кайсыл сөздүн синоними катары колдонулат?
"Тең күчтүү"
"Жана"
"Же"
"Каалагандай"
Көптүк деген эмне?
Кандайдыр бир объектилердин жыйындысы
Функциялардын тобу
Цифралардын саны
Сандардын аталышы
Көптүк теориясын негиздөөчүлөрдүн бири ким?
Георг Кантор
Ньютон
Лейбниц
Декарт
Көптүктөр теориясы качан пайда болгон?
ХIX кылымдын аягында
XX кылымдын аягында
VII кылымдын орто ченинде
XXI кылымдын башында
кандай жол менен берилди?
Көптүктүн элементтеринин касиетин баяндоо жолу
Көптүктүн элементтерин баяндоо жолу
Элементтерин баяндоо жолу
Тартипке келтирүү жолу
x элементи Х көптүгүнө таандык дегенди кандай белгилейбиз?




x элементи Х көптүгүнө таандык эмес дегенди кандай белгилейбиз?




Эгерде А көптүгүнүн бардык элементтери В көптүгүнүн да элементтери болсо, анда А көптүгү В көптүгүнүн . . . деп аталат.
Бөлүкчө көптүгү
Камтылган көптүгү
Универсал көптүгү
Булеаны
Эйлер-Венндин диограммасы деп - көптүктөрдүн ... аркылуу сүрөттөлүшүн айтабыз.
Жалпак фигуралар
Томпок фигуралар
Ийри фигуралар
Түз сызык
Көптүктөрдүн кесилишүүсүнүн коммутативдүүлүк касиетин жазгыла.
|B(U)| - аркылуу U көптүгүнүн ... белгилейбиз.
Кубаттуулугун
Булеанын
Кесилишүүсүн
Биригүүсүн
U көптүгүнүн кубаттуулугунун формуласын жазгыла.


Көптүктөрдүн декарттык көбөйтүндүсү кандай белгиленет?




a нын bга болгон катышы кандай белгиленет?




Бинардык катыш канча түргө бөлүнөт?
5
4
3
2
А={3,6,9,12,15} жана B={6,1,2,5,9,13} көптүктөрүнүн биригүүсүн тап.
А={3,6,9,12,15} жана B={6,1,2,5,9,13} көптүктөрүнүн кесилишин тап.
экендиги белгилүү болсо,
9
20
10
1
экендиги белгилүү болсо,
10
9
16
42
Далилдөөсүз кабыл алынган математикалык сүйлөм ... деп аталат.
Аксиома
Теорема
Аныктама
Айтылыш
Далилдөөнү талап кылуучу математикалык сүйлөм ... деп аталат.
Теорема
Аксиома
Аныктама
Айтылыш
Бул диаграмма көптүктөрдүн кайсыл амалына таандык?
Биригүү
Айырма
Толуктоосу
Кесилишүү
“∀” символу кайсыл сөздүн синоними катары колдонулат?
“Каалагандай”
“Жашайт”
“Жана”
“Бирөө гана”
Ар бир байланыш компоненти кайрадан дарак болгон байланышпаган граф . . . деп аталат?
Дарак
Дарактын бутактары
Дарактын хордасы
Токой
формуласы . . . деп аталат?
Ньютондун биному
Бернуллинин формуласы
Де Моргандын формуласы
Эйлер-Венндин диаграммасы
32 санынын экилик эсептөө системасындагы көрүнүшүн жазгыла?
1000002
322
100112
22222
"∃" символу кайсыл сөздүн синоними катары колдонулат?
“Канча”
“Бирөө гана”
“Жана”
“Жашайт”
112 санын ондук системага өткөргүлө.
3
9
6
7
Класста дежур болуу үчүн бир жумага 6 окуучу бөлүнгөн. Канча түрдүү жол менен кезекти уюштурууга болот?
720
6
12
16
 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?
24
4
12
7
Жалпы бүтүмдөрдүн негизинде бир жеке бүтүмгө келүүнү ... деп түшүнөбүз.
Дедукция усулу
Индукция усулу
Жекече усул
Жалпылоо усулу
Бардык мүмкүн болгон айрым учурларды кароонун негизинде жалпы тыянакка келүү ... деп аталат.
Толук индукция
Толук эмес индукция
Толук дедукция
Толук эмес дедукция
“∧” символу кайсыл сөздүн синоними катары колдонулат?
“Жана”
“Жашайт”
“Каалагандай”
"Же"
0 жана 1 цифраларын колдонуп, үч орундуу канча сан жазса болот?
4
3
2
1
Илимий конференцияга келген 5 окумуштуу бири-бири менен кол алышып учурашышты. Баары канча жолу кол алышып учурашылды?
10
5
120
25
Токойдо 6 жаныбар жолугуп калышты: карышкыр, түлкү, жолборс, аюу, маймыл жана пил. Алар бири-бири менен кол алышып учурашышты. Кол алышып учурашуу канча жолу болду?
15
6
10
25
Айназиктин 2 конверти болгон: жөнөкөй жана авиалык, ошондой эле, үч маркасы болгон: тик бурчтуу, квадрат, үч бурчтуу. Катты жөнөтүш үчүн Айназик конверт менен марканы канча жол менен тандашы мүмкүн.
6
3
2
5
Графтар теориясы 1736-жылдагы Л.Эйлердин ... чыгарылышын аныктаганы менен пайда болгон.
“Кенигсберг көпүрөлөрү жөнүндөгү маселени”
"Жолдорду аныктоо маселесинин"
"Кыска убакытты аныктоо маселесинин"
"Планеталарды жайгаштыруу маселесинин"
Леонард Эйлер - математик, физик, астроном, механик кайсыл жылдары жашаган?
1707-1783
1804-1888
1778-1955
569-632
Чокулардын көптүгүн ... аркылуу белгилейбиз.
G=〈E,V〉
Билбейм
Графты кыскача ... деп белгилейбиз.

Билбейм
Берилген таблицаны пайдаланып граф түзгүлө.
Багытталган кабырга?
Жаа
Бутак
Кабырга
Дарак
Дарактагы кабыргалар эмне деп аталат?
Бутак
Жаа
Бүчүр
Кабырга
Граф терминин киргизген окумуштуу?
Денеш Кениг
Лейбниц
Эйлер
Даламбер
Ал эми, “граф” термини биринчи жолу 200 жылдан кийин, ... Венгер математиги Денеш Кениг тарабынан киргизилген.
1936-жылы
1836-жылы
1736-жылы
1636-жылы
Бул эмне?
Граф
Планета
Схема
Фигура
Бир чокудан чыгып кайра ошол чокуга кирген сызык?
Сыйыртмак
Чынжыр
Кабырга
Жаа





Графтагы чекиттер?
Чокулар
Кабыргалар
Жаалар
Бутактар
Дисциплинанын окуу-усулдук жана маалыматтык жактан камсыздалышы
Негизги адабияттар
С.Д. Шапорев. Дискретная математика. Санк.-Петерб., 2009
Т.Н. Энназаров. Математиканын башталгыч курсунун негиздери. Ж-А., 2006
С.П. Лавров. Математическое программирование. М.-Наука, 1986
А.И. Горбатов. Основы дискретной математики. М.-Наука, 1987
А.В. Чередникова. Дискретная математика. КГТУ, 2011
В.И. Носова. Элементы теории графов. Новосибирск, 2008
Андерсон Дж. Дискретная математика и комбинаторика. – М.: Издательство «Вильямс», 2004
Кузнецов О.П. Дискретная математика для инженера. – СПб.: Изд-во «Лань», 2004.
Самарский А.А., Гулин А.В. Численные методы. – М.: ВШ,1989
Демидович Б.П., Марон И.А. Численные методы анализа. – М.: Наука,1967
Калманбетов М.К., Болотбаев К.Б., Эсеналиева Н.К. Численные методы. Часть I. -Жалалабат, ЦИТ ЖАГУ, 2002
Кошумча адабияттар
Плотников А.Д. Дискретная математика: учебное пособие. – М.: Изд-во «Новое знание», 2005.
Судоплатов С.В., Овчинникова Е.В. Дискретная математика. – М.: Изд- во «ИНФРА-М», 2005.
Палий И.А. Дискретная математика. Курс лекций. – М.: Изд-во «ЭКСМО», 2008.
Офицеров В.В. Дискретная математика. Учебное пособие.– Томск: Издательство ТПУ, 2005.
Новиков Ф.А. Дискретная математика для программистов. – Спб.: Изд-во «Питер», 2004.
Воробьев Г. Н., Данилова А. Н. Практикум по численным методам.- М.: Высшая школа, 2007
Программалык жактан камсыздалышы
230109 “Эсептөө техникасын жана автоматташтырылган системаларды программалык камсыздоо” адистиги боюнча орто кесиптик билим берүүчү мамлекеттик стандарттын (ОКББ МС), ОПОП, ОМК, Силлабус.
Маалыматтык-сурап билүүчү, издеп табуучу системалардын базасы
https://www.twirpx.com/533683/
https://infourok.ru/
https://www.okuma.kg
https://arch.kyrlibnet.kg
https://www.ibekboev.narod.ru
ЖАМУнун абонементтик бөлүмүнөн жана окуу залынан.
Жалал-Абад шаардык китепканасынын окуу залынан.







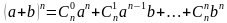 формуласы . . . деп аталат?
формуласы . . . деп аталат?
 канчага барабар?
канчага барабар? туюнтмасынын маанисин эсептегиле.
туюнтмасынын маанисин эсептегиле.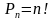
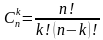
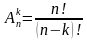
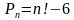
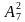 туюнтмасынын маанисин эсептегиле?
туюнтмасынын маанисин эсептегиле?









