Дистанционный курс "Комбинаторика" для СПО

Дистанционный курс

Наименование дисциплины Математика

ФИО разработчик Добрынина Надежда Владимировна

Занимаемая должность преподаватель количество часов – 6

Плановая дата разработки 20.12.2018

Плановая дата внедрения дистанционного курса II семестр 2018-2019 учебного года

Комплекс задач по теме «Комбинаторика»

1. Сколько существует трехзначных чисел, в записи которых все цифры нечетные?

2. Электронный кодовый замок имеет клавиатуру с цифрами от 0 до 9. Каково число четырехзначных кодов?

3. Механический кодовый замок имеет клавиатуру с цифрами от 0 до 9. Каково число четырехзначных кодов?

4. Сколькими способами можно уложить в ряд 2 зеленые и 4 красные папки?

5. Инвестор формирует портфель ценных бумаг. Он может вложить деньги в ацкии 5 различных фирм. Сколько существует способов создать портфель из 7 акций?

6. Студентам (12 человек) необходимо пройти обследование врача. Сколькими способами можно составить список на прием к врачу?

7. В селе 1,5 тысячи жителей. Докажите, что по крайней мере 2 из них имеют одинаковые инициалы.

8. В составе поезда Москва – Саратов 3 купейных, 4 плацкартных и 2 общих вагона. Сколько существует способов сформировать состав?

9. 7 книг расставляют на 1 полке. Сколько существует способов расставить книги так, чтобы 2 определенные книги стояли рядом?

10. Сколькими способами можно выбрать 4 монеты из 5 рублевых и 4 двухрублевых?

11. Сколько трехзначных чисел можно составить из четных цифр без повтора?

12. Сколько четырехзначных чисел делящихся на 5 без остатка можно составить из цифр 0,1,3,5,7 без повтора?

13. На начальной остановке в вагон метро вошли 100 человек. Сколькими способами они могут выйти на последней 16 остановке?

14. В урне 15 шариков: 10 черных и 5 белых. Сколькими способами можно извлечь из урны 5 шариков, чтобы 3 белых и 2 черных?

15. Сколько различных звукосочетаний можно взять на 10 выбранных клавишах рояля, если каждое звукосочетание содержит от 3 до 10 звуков без повторов?

16. Сколько четырехзначных чисел из цифр 0,1,2,3,4,5 содержат цифру 3?

17. Лифт, в котором находятся 9 пассажиров, может остановиться на 10 этажах. Пассажиры выходят группами по 2,3 и 4 человека. Сколькими способами это может произойти?

Дистанционный курс по математике для студентов 1 курса

Преподаватель: Добрынина Н.В.

Лекция № 2

Тема: Правила комбинаторики.

Цели лекции:

• Рассмотреть основные правила комбинаторики и их применение.

• Формировать навыки решения комбинаторных задач.

Все расчетные формулы комбинаторики базируются на двух основных правилах:

1. Правило суммы.

Если элемент х из исходного множества можно выбрать n способами, после чего элемент у можно выбрать m способами, тогда выбрать либо х, либо у можно n+m способами.

Задача 1: Сколькими способами можно выбрать подарок ребёнку из 9 машинок, 7 плюшевых медведей и 3 железных дорог?

Решение: по правилу сложения 9 + 7 + 3 = 19 способами. 

Ответ: 19.

1. Правило произведения

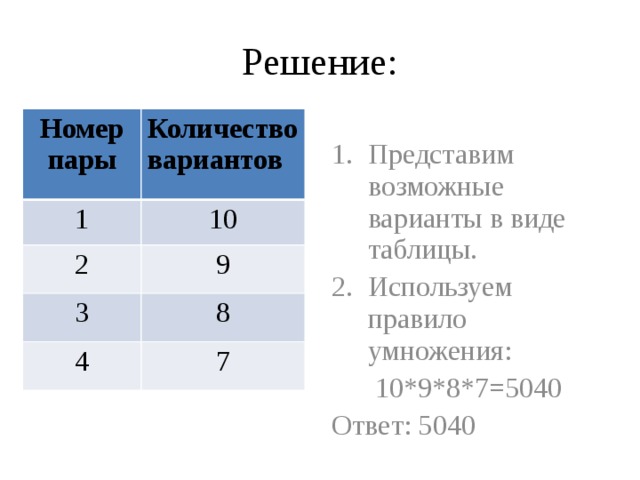
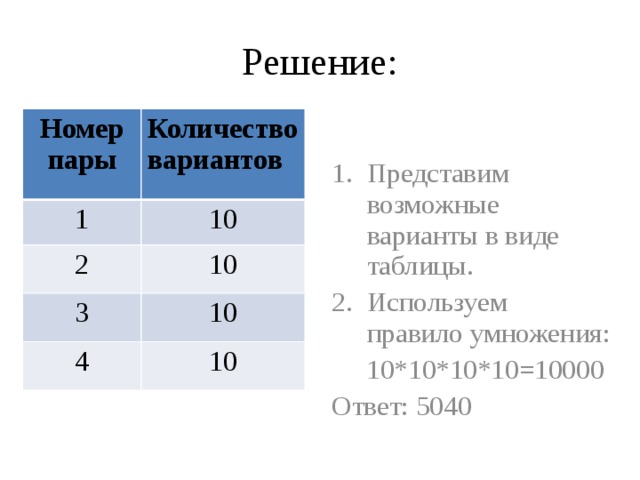
Задача 2: В группе изучают 10 предметов. Сколькими способами можно составить расписание на понедельник, если известно, что все пары должны быть различными и их 4?

Решение: Представим возможные варианты в виде таблицы.

Используем правило умножения: 10*9*8*7=5040

Ответ: 5040

1. Применение правил комбинаторики.

Задача 3: Сколько трёхзначных чисел можно составить из цифр 0, 2, 4, 6, 8, используя в записи числа каждую из них не более одного раза?

Решение: 0 не может стоять первым, значит первую цифру нужно выбрать из 2, 4, 6, 8 — 4 способа; второй цифрой может быть любая из четырёх оставшихся — 4 способа; третью цифру можно выбрать среди трёх оставшихся — 3 способа.

Итак, искомое количество трёхзначных чисел: 4 · 4 · 3 = 48. 

Ответ: 48. 

Задача 4:  Из пункта А в пункт В ведут 3 дороги, а из пункта В в пункт С – 4 дороги. Сколькими способами можно совершить поездку из А в С через В?

Решение: В пункте А есть 3 способа выбора дороги в пункт В, а в пункте В есть 4 способа попасть в пункт С. Согласно принципу умножения, существует 34=12 способов попасть из пункта А в пункт С.

Ответ: 12.

Задача 5: Имеется 5 видов конвертов без марок и 4 вида марки. Сколькими способами можно выбрать конверт и марку для посылки письма?

Решение: 5*4=20

Ответ: 20

Задача 6:  На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и потом спуститься с неё? Решите ту же задачу при дополнительном условии, что подъём и спуск происходят по разным дорогам.

Решение: 5*5=25; 5*4=20

Ответ: 25; 20.

Задача 7:  При составлении одного варианта письменной контрольной работы по математике преподаватель располагает 4 задачами по геометрии, 8 – по алгебре и 3 – по тригонометрии. Сколькими способами можно составить этот вариант, если в него должно войти по одной задаче из перечисленных разделов?

Решение: 8*4*3=96

Ответ: 96.

Задача 8: Из двух полуфинальных групп, каждая их которых содержит по 6 команд, в финал выходит по одной команде. Сколько может быть различных вариантов участников финального матча?

Решение: 6*6=36.

Ответ: 36.

Задача 9:  В книге из 20 страниц на каких-либо трех страницах надо поместить по одной разной иллюстрации. Сколькими способами это можно сделать?

Решение: 20*19*18=1640

Ответ: 1640.

Задача 10.   На складе имеются 6 ящиков с различными фруктами и 3 ящика с различными овощами. Сколькими способами можно каждой из двух овощных палаток выдать по одному ящику с фруктами и овощами?

Решение: 3*6*5*2=180

Ответ: 180.

Задача 11:  Пусть из города A в город B можно добраться одним авиамаршрутом, двумя железнодорожными маршрутами и тремя автобусными маршрутами. Сколькими способами можно добраться из города A в город B?

Решение: Все условия принципа сложения здесь выполнены, поэтому, в соответствии с этим принципом, получим 1+2+3=6 способов.

Задача 12:  В магазине электроники продаются три марки телевизоров и два вида видеомагнитофонов. У покупателя есть возможности приобрести либо телевизор, либо видеомагнитофон. Сколько способами он может совершить одну покупку? Сколько различных комплектов, содержащих телевизор и магнитофон, можно приобрести в этом магазине, если покупатель собирается приобрести в паре и телевизор, и видеомагнитофон?

Решение: Один телевизор можно выбрать тремя способами, а магнитофон – другими двумя способами. Тогда телевизор или магнитофон можно купить 3+2=5 способов.

Во втором случае один телевизор можно выбрать тремя способами, после этого видеомагнитофон можно выбрать двумя способами. Следовательно, в силу принципа умножения, купить телевизор и видеомагнитофон можно 32=6 способами.

Ответ: 5; 6.

Замечание. Обычно принцип сложения применяется в тех случаях, когда в задачах встречаются союзы «или», «либо, либо» (телевизор или видеомагнитофон), а принцип умножения – в задачах, содержащих союз «и» (телевизор и видеомагнитофон).

Рассмотрим теперь примеры, в которых применяются оба правила комбинаторики: и принцип умножения, и принцип сложения.

Задача 13:  В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает либо яблоко, либо апельсин, после чего Надя выбирает из оставшихся фруктов и яблоко и апельсин. Сколько возможно таких выборов?

Решение: Ваня может выбрать яблоко 12 способами, апельсин – 10 способами. Если Ваня выбирает яблоко, то Надя может выбрать яблоко 11 способами, а апельсин – 10 способами. Если Ваня выбирает апельсин, то Надя может выбрать яблоко 12 способами, а апельсин – 9 способами. Таким образом, Ваня и Надя могут сделать свой выбор 12*11*10+10*12*9 = 2400 способами.

Ответ: 2400

Задача 14: Есть 3 письма, каждое из которых можно послать по 6 адресам. Сколькими способами это можно сделать?

Решение. В данной задаче мы должны рассмотреть три случая: а) все письма рассылаются по разным адресам, б) все письма посылаются по одному адресу, в) только два письма посылаются по одному адресу. Если все письма рассылаются по разным адресам, то число таких способов легко находится из принципа умножения: n₁=654=120 способов. Если все письма посылаются по одному адресу, то таких способов будет n₂=6. Таким образом, остается рассмотреть только третий случай, когда только 2 письма посылаются по одному адресу. Выбрать какое-либо письмо мы можем 3 способами и послать его по какому-либо выбранному адресу можем 6 способами. Оставшиеся два письма мы можем послать по оставшимся адресам 5 способами. Следовательно, послать только два письма по одному адресу мы можем n₃=365=90 способами. Таким образом, разослать 3 письма по 6 адресам в соответствие с принципом сложения можно n₁+n₂+n₃ = 120+6+90 = 216 способами.

Ответ: 216.

Задача 15:  В урне содержится 3 синих, 5 красных и 2 белых шара. Сколькими способами можно вытащить из урны либо два белых шара, либо два цветных шара, из которых один синий, а другой – красный?

Решение: Все шары различимы и порядок важен. Поэтому способов вытащить два цветных шара по правилу умножения: 3*5=15. А вытащить 2 белых шара – 2 способа. Итого всего по правилу сложения 15+2=17 способов.

Ответ: 17.

Задача 16:  Имеется 6 различных конвертов без марок, 4 различные марки и 3 различных конверта с марками. Сколькими способами можно выбрать конверт с маркой для отправки письма?

Решение: по правилу умножения 6*4=24 – способы наклеить марку на конверт. По правилу сложения 24+3= 27 способов выбрать конверт с маркой.

Ответ: 27.

Задача 17: Семья новоселов хочет приобрести письменный стол, книжный шкаф и диван. В мебельном магазине имеется 6 письменных столов, 4 книжных шкафа и 12 диванов, Кроме того, есть 2 гарнитура, содержащих письменный стол и диван, и 8 гарнитуров, содержащих книжный шкаф и письменный стол. Сколькими способами может быть сделана покупка?

Решение: Возможны три варианта покупки мебели: 1) По правилу умножения найдем способы выбрать стол, шкаф и диван не из гарнитура 6*4*12=288. 2) Также семья может приобрести гарнитур из стола и дивана и шкаф отдельно. Найдем по правилу умножения количество вариантов: 2*4=8. 3) Или семья может приобрести гарнитур из шкафа и стола, а диван отдельно. Тогда по правилу умножения количество вариантов равно 8*12=96. Найдем по правилу сложения общее количество вариантов 288+8+96=392.

Ответ: 392.

Задача 18: В букинистическом магазине лежат 6 разных изданий романа И.С. Тургенева «Рудин», 3 издания его романа «Дворянское гнездо» и 4 издания романа «Отцы и дети». Кроме того, есть 5 разных сборников, в каждом из которых есть романы «Рудин» и «Дворянское гнездо», и 7 сборников с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?

А если в магазине есть ещё 3 сборника, содержащие романы «Рудин» и «Отцы и дети», и 5 книг, содержащих все три романа?

Решение: 1) Можно купить либо по экземпляру каждого романа, либо сборник, содержащий два романа, и экземпляр третьего романа. Из принципов сложения и умножения получаем, что купить три романа отдельно можно 6*3*4=72 способами. Во втором случае можно купить сборник, содержащий романы «Рудин» и «Дворянского гнезда» и один экземпляр «Отцы и дети». Тогда вариантов будет 5*4=20. В третьем случае можно купить сборник с романами «Дворянское гнездо» и «Отцы и дети» и отдельно «Рудин». Тогда вариантов 7*6=42. Всего по правилу сложения имеем 72+20+42=134 способов.

2) Если в магазине есть еще сборники, содержащие романы «Рудин» и «Отцы и дети», и 5 книг, содержащих все три романа, то возможны еще способы. При покупке сборника «Рудин» и «Отцы и дети» и отдельно романа «Дворянское гнездо» 3*7=21 способ. При покупке сборника с тремя романами – 5 способов. По правилу сложения получаем 134+21+5=160.

Ответ: 134; 160.

Список литературы и Интернет-ресурсов:

1. Новоселов О.В. Комбинаторика и вероятность: учебн. пособие для слушателей подготовит. курсов / О. В. Новоселов, Л.П. Скиба. СибГАУ, Красноярск, 2009. – 78 с.

2. Филимонова Л.В., Быкова Е.А. Математика и информатика. Учебное пособие (для студентов гуманитарных факультетов ВУЗов). – 2-е изд. Дополненное и переработанное – Елец, ЕГУ им. И.А. Бунина, 2001, 110 с.

3. http://math4school.ru/elementy_kombinatoriki

ГАПОУ МО «Подмосковный колледж «Энергия»

Тема 2: Правила комбинаторики

Дистанционный курс по математике для студентов 1 курса

Преподаватель: Добрынина Н.В.

Правила комбинаторики

• Правило суммы: если элемент х из исходного множества можно выбрать n способами, после чего элемент у можно выбрать m способами, тогда выбрать либо х, либо у можно n+m способами.
• Правило произведения: если элемент х из исходного множества можно выбрать n способами, после чего элемент у можно выбрать m способами, тогда выбрать упорядоченную пару (х;у) можно n*m способами.

Задача:

В группе изучают 10 предметов. Сколькими способами можно составить расписание на понедельник, если известно, что все пары должны быть различными и их 4?

Решение:

Номер пары

Количество вариантов

1

10

2

9

3

8

4

7

• Представим возможные варианты в виде таблицы.
• Используем правило умножения:

10*9*8*7=5040

Ответ: 5040

Как будет решаться задача, если пары могу повторяться?

Решение:

Номер пары

Количество вариантов

1

10

2

10

3

10

4

10

• Представим возможные варианты в виде таблицы.
• Используем правило умножения:

10*10*10*10=10000

Ответ: 5040

Список литературы:

• Новоселов О.В. Комбинаторика и вероятность: учебн. пособие для слушателей подготовит. курсов / О. В. Новоселов, Л.П. Скиба. СибГАУ, Красноярск, 2009. – 78 с.
• Филимонова Л.В., Быкова Е.А. Математика и информатика. Учебное пособие (для студентов гуманитарных факультетов ВУЗов). – 2-е изд. Дополненное и переработанное – Елец, ЕГУ им. И.А. Бунина, 2001, 110 с.
• http://math4school.ru/elementy_kombinatoriki

Спасибо за внимание!

ГАПОУ МО «Подмосковный колледж «Энергия»

Тема 1: Сочетания. Размещения. Перестановки.

Дистанционный курс по математике для студентов 1 курса

Преподаватель: Добрынина Н.В.

Комбинаторика

Занимается задачами о существовании и подсчете различных комбинаций, которые можно составлять и элементов заданного конечного множества.

Задача: На какую сумму очков выгоднее поставить ставку, если очки выпадают при подбрасывании двух игральных костей?

Решение:

1 . Рассмотрим возможные варианты.

2. Представим полученные результаты в таблице.

3. Видно, что  целесообразно сделать ставку на выпадение  сумме 7 очков, поскольку она получается наибольшим количеством вариантов.

Ответ: 7.

Сумма очков

2

Число способов

Возможные варианты

1

3

4

1 + 1

2

3

5

1 + 2; 2 + 1

1 + 3; 3 + 1; 2 + 2

6

4

1 + 4; 4 + 1; 2 + 3; 3 + 2

5

7

6

1 + 5; 5 + 1; 2 + 4; 4 + 2; 3 + 3

8

1 + 6; 6 + 1; 2 + 5; 5 + 2; 3 + 4; 4 + 3

5

9

2 + 6; 6 + 2; 3 + 5; 5 + 3; 4 + 4

10

4

11

3

3 + 6; 6 + 3; 4 + 5; 5 + 4

4 + 6; 6 + 4; 5 + 5

12

2

5 + 6; 6 + 5

1

6 + 6

Факториал числа N

- произведение всех натуральных чисел от 1 до n, включая n.

Пример: 5!

Решение: 5! = 1*2*3*4*5= 120

Пример:

Решение:

пример:

Решение:

Основные формулы комбинаторики

Перестановки

Перестановками из n различных элементов называются все возможные последовательности этих элементов. P n - перестановка .

{a, b, c} – множество элементов

Перестановки: abc, acb, bac, bca, cab, cba.

P n =n!

P 3 =3!=1*2*3= 6

перестановки

Перестановками с повторениями из n элементов k типов, причем 1 типа – n 1 штук, 2 типа – n 2 штук, 3 типа – n 3 штук и так далее, называются все возможные последовательности исходных элементов .

{a, b, а} – множество элементов

Перестановки: aаb, baа, аba.

Задача:

Сколькими способами можно переставить буквы в слове «ананас»?

Решение:

Всего букв 6.

Из них одинаковы n 1 «а»=3, n 2 «н»=2, n 3 «с»=1.

Размещения

Размещениями из n различных элементов по m элементов, взятых из исходного множества, называются все возможные последовательности из m элементов, которые отличаются составом элементов или порядком их следования. (А n m )

{a, b, c} – множество элементов

Размещения: ab, ac, bc, ba, cb, ca.

Размещения

Размещениями с повторениями из элементов n различных типов по m элементов, взятых из исходного множества, называются все возможные последовательности из m элементов, которые отличаются составом элементов или порядком их следования. (А n m )

{a, b, c} – множество элементов

Размещения: ab, aa, ba, bb, cb, ca, ac, cc, bc.

Сочетания

Сочетаниями из n различных элементов по m элементов называются все такие последовательности из m элементов, взятых из исходного множества. (C n m )

{a, b, c} – множество элементов

Сочетания: ab, cb, ac.

Задача:

В первенстве по футболу участвует 16 команд, причем любые 2 играют между собой 1 матч. Сколько игр будет сыграно?

Решение:

n=16, m= 2

Сочетания

Сочетаниями c повторениями из n различных элементов по m элементов называются все такие последовательности из m элементов, взятых из исходного множества. (C n m )

{a, b, c} – множество элементов

Сочетания: ab, cb, ac, aa, bb, cc.

Задача:

В кондитерской имеется 5 различных видов пирожных. Сколькими способами можно составить набор из4 пирожных?

Решение:

n= 5, m=4

Замечания:

• При использовании в задаче формул перестановок из элементов исходного множества не происходит выбор.
• Сочетания применяются в задачах, где не важен порядок следования элементов. Размещения применяются, где порядок следования элементов имеет принципиальное значение.

Схема решения комбинаторных задач

Начало

Есть ли в задаче выбор?

ДА

Важен ли порядок?

Перестановка

НЕТ

Сочетание

Размещение

Могут ли элементы повторяться?

С повтором

Без повтора

Задача 6: Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет .

Решение: P n  =n! = 4! = 1  2  3  4 = 24 .

Задача 7: Имеется 5 кружков: 3 белых и 2 черных.

Сколько различных узоров можно получить,

располагая кружки в ряд.

.

Задача 8: Сколько словарей надо издать,

чтобы можно было непосредственно выполнить

перевод с любого из 5 языков на любой

из 5 языков.

Задача 9: На железнодорожной станции имеется

5 светофоров. Сколько может быть дано

различных комбинаций их сигналов, если

каждый светофор имеет 3 состояния.

Задача 10 : 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой.

Задача 11: В цветочном магазине продаются цветы 6 видов. Сколько можно составить букетов из 10 цветов в каждом (букеты отличающиеся лишь расположением цветов считать одинаковыми).

.

.

Задача 12: В группе 20 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.

165*5*4=3300

Задача 13: Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.

24*60*120= 172800

Список литературы:

• Новоселов О.В. Комбинаторика и вероятность: учебн. пособие для слушателей подготовит. курсов / О. В. Новоселов, Л.П. Скиба. СибГАУ, Красноярск, 2009. – 78 с.
• Филимонова Л.В., Быкова Е.А. Математика и информатика. Учебное пособие (для студентов гуманитарных факультетов ВУЗов). – 2-е изд. Дополненное и переработанное – Елец, ЕГУ им. И.А. Бунина, 2001, 110 с.
• http://math4school.ru/elementy_kombinatoriki

Спасибо за внимание!