Просмотр содержимого документа
«Длина окружности и площадь круга. Контрольная работа»
Длина окружности и площадь круга.
Контрольная работа
1. Найдите длину окружности, описанной около треугольника АВС, если АВ = 6 см, угол С равен 600.
см, угол С равен 600.
2. Чему равно отношение площади квадрата к площади, вписанного в него круга?
3. Одна из сторон треугольника равна 30 см, а другая сторона делится точкой касания вписанной окружности на отрезки 12 см и 14 см, считая от конца неизвестной стороны. Найдите площадь вписанного круга.
Решение
1
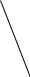
 . А
. А

В С
Длина окружности вычисляется по формуле С = 2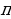 R. Чтобы найти длину радиуса описанной около треугольника окружности, воспользуемся теоремой синусов в её расширенном виде:
R. Чтобы найти длину радиуса описанной около треугольника окружности, воспользуемся теоремой синусов в её расширенном виде: 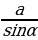 =
=  =
=  = 2R. Отсюда найдём R=
= 2R. Отсюда найдём R=  . R =
. R = 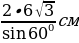 =
= 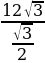 см = 24 см. Следовательно
см = 24 см. Следовательно
С = 2 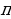
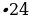 см = 48
см = 48
2
 .
.
Радиус круга, вписанного в квадрат, равен половине стороны квадрата. Тогда площадь круга равна 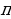 R2, а площадь квадрата равна (2R)2 = 4R2. Отсюда, отношение площади квадрата к площади круга найдём:
R2, а площадь квадрата равна (2R)2 = 4R2. Отсюда, отношение площади квадрата к площади круга найдём:
4R2 : 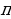 R2 = 4 :
R2 = 4 : 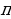 .
.
3


 . А
. А
12см
М К
14 см
В 30см N C
Круг вписан в треугольник АВС и касается сторон треугольника в точках М, N, и К. По условию АК = 12см, КС = 14 см, ВС = 30 см. По свойству отрезков касательных, проведённых из одной точки к окружности, имеем: АК = АМ = 12см, СК = СN = 14 см. Учитывая, что сторона ВС = 30см, найдём ВN = 30см – 14 см = 16см. Следовательно, ВМ = ВN = 16см. Отсюда, стороны треугольника равны: АС = 12см + 14см = 26см, АВ = 12см + 16см = 28см. По формуле Герона найдём площадь треугольника АВС. S = 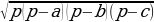 , где p =
, где p = 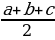 . p =
. p =  = 42.
= 42.
S =  =
= 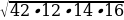 =
= 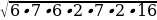 = 6
= 6 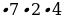 = 336 (cм2). С другой стороны, площадь треугольника можно найти по формуле: S = pr. Тогда r = S: p. r = 336см2: 42см = 8см. А площадь вписанного круга будет равна: S =
= 336 (cм2). С другой стороны, площадь треугольника можно найти по формуле: S = pr. Тогда r = S: p. r = 336см2: 42см = 8см. А площадь вписанного круга будет равна: S =  . S =
. S = 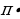 82 = 64
82 = 64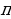 cм2.
cм2.







 см, угол С равен 600.
см, угол С равен 600.
 . А
. А
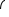
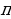 R. Чтобы найти длину радиуса описанной около треугольника окружности, воспользуемся теоремой синусов в её расширенном виде:
R. Чтобы найти длину радиуса описанной около треугольника окружности, воспользуемся теоремой синусов в её расширенном виде: 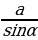 =
=  =
=  = 2R. Отсюда найдём R=
= 2R. Отсюда найдём R=  . R =
. R = 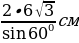 =
= 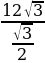 см = 24 см. Следовательно
см = 24 см. Следовательно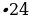 см = 48
см = 48

 .
. 


 . А
. А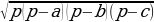 , где p =
, где p = 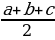 . p =
. p =  = 42.
= 42. =
= 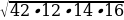 =
= 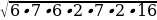 = 6
= 6 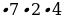 = 336 (cм2). С другой стороны, площадь треугольника можно найти по формуле: S = pr. Тогда r = S: p. r = 336см2: 42см = 8см. А площадь вписанного круга будет равна: S =
= 336 (cм2). С другой стороны, площадь треугольника можно найти по формуле: S = pr. Тогда r = S: p. r = 336см2: 42см = 8см. А площадь вписанного круга будет равна: S =  . S =
. S = 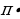 82 = 64
82 = 64









