
В заметках даны рекомендации по работе с каждым слайдом

Ο
1
2
3
4
5
6
7
8
Слайд выбора задачи. Нажимаем на кнопку – переходим на слайд с задачей.

№ 1
Определите направление ветвей
и координаты вершины параболы:
1)
(5; – 5)
Ветви
вверх
Ветви
(1,5; – 1,75)
вниз
2)
( – 6; – 1)
Ветви
вверх
3)
Для проверки правильности ответа необходимо нажать на прямоугольник с функцией ДВА раза
( – 2; 26)
Ветви
вниз
4)

№ 2
Постройте график функции:
5)
1)
2)
6)
3)
7)
Слайд выбора функции. Для проверки правильности построения графика необходимо нажать на прямоугольник с функцией. После нажатия переходим на слайд проверки. После возврата на данный слайд выбираем следующую функцию.
8)
4)
 0 → ветви вверх 5 Вершина ( – 3; – 4) Ох : ( – 1; 0) и ( – 5; 0) Оу : ( 0; 5 ) -3 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 6 – 4 – 2 5 – 3 – 3 у -4 5 " width="640"
0 → ветви вверх 5 Вершина ( – 3; – 4) Ох : ( – 1; 0) и ( – 5; 0) Оу : ( 0; 5 ) -3 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 6 – 4 – 2 5 – 3 – 3 у -4 5 " width="640"
№ 2
Постройте график функции:
1)
a 0 → ветви вверх
5
Вершина ( – 3; – 4)
Ох : ( – 1; 0) и ( – 5; 0)
Оу : ( 0; 5 )
-3
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
х
– 6
– 4
– 2
5
– 3
– 3
у
-4
5

№ 2
Постройте график функции:
2)
a 0 → ветви вниз
4
Вершина ( 1; 4 )
Ох : ( – 1; 0) и (3; 0)
Оу : ( 0; 3 )
1
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
4
2
– 2
х
– 5
– 5
у
3
6
 0 → ветви вверх Вершина ( – 1; – 4,5) Ох : ( – 4; 0) и ( 2; 0) -1 Оу : ( 0; – 4 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 – 2 – 5 х 3,5 – 4 3,5 у -4,5 7 " width="640"
0 → ветви вверх Вершина ( – 1; – 4,5) Ох : ( – 4; 0) и ( 2; 0) -1 Оу : ( 0; – 4 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 – 2 – 5 х 3,5 – 4 3,5 у -4,5 7 " width="640"
№ 2
Постройте график функции:
3)
a 0 → ветви вверх
Вершина ( – 1; – 4,5)
Ох : ( – 4; 0) и ( 2; 0)
-1
Оу : ( 0; – 4 )
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
3
– 2
– 5
х
3,5
– 4
3,5
у
-4,5
7
 0 → ветви вверх Вершина ( 1; 0 ) Ох : ( 1; 0 ) Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 2 – 1 х 3 12 3 12 у 1 8 " width="640"
0 → ветви вверх Вершина ( 1; 0 ) Ох : ( 1; 0 ) Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 2 – 1 х 3 12 3 12 у 1 8 " width="640"
№ 2
Постройте график функции:
4)
a 0 → ветви вверх
Вершина ( 1; 0 )
Ох : ( 1; 0 )
Оу : ( 0; 3 )
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
3
2
– 1
х
3
12
3
12
у
1
8
 0 → ветви вверх Вершина ( – 2; – 4) Ох : ( – 4; 0) и (0; 0) Оу : ( 0; 0 ) -2 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 0 х – 5 – 1 1 5 5 – 3 у -4 9 " width="640"
0 → ветви вверх Вершина ( – 2; – 4) Ох : ( – 4; 0) и (0; 0) Оу : ( 0; 0 ) -2 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 0 х – 5 – 1 1 5 5 – 3 у -4 9 " width="640"
№ 2
Постройте график функции:
5)
a 0 → ветви вверх
Вершина ( – 2; – 4)
Ох : ( – 4; 0) и (0; 0)
Оу : ( 0; 0 )
-2
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
0
х
– 5
– 1
1
5
5
– 3
у
-4
9

№ 2
Постройте график функции:
6)
4
a 0 → ветви вниз
Вершина ( 0; 4 )
Ох : ( – 2; 0) и ( 2; 0)
Оу : ( 0; 4 )
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
3
1
– 1
х
– 5
3
3
у
10

№ 2
Постройте график функции:
7)
a 0 → ветви вниз
5
Вершина ( 5; 0 )
Ох : ( 5; 0)
Оу : ( 0; – 5 )
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
7
1
– 1
х
-5
– 0,8
– 3,2
– 7,2
у
11
 0 → ветви вверх Вершина ( 1; 2 ) Ох : НЕТ Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 2 2 3 3 2 6 3 11 у 1 12 " width="640"
0 → ветви вверх Вершина ( 1; 2 ) Ох : НЕТ Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 2 2 3 3 2 6 3 11 у 1 12 " width="640"
№ 2
Постройте график функции:
8)
a 0 → ветви вверх
Вершина ( 1; 2 )
Ох : НЕТ
Оу : ( 0; 3 )
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
х
– 2
2
3
3
2
6
3
11
у
1
12
 0 → ветви вверх Вершина ( 1; – 4) Ох : ( – 1; 0) и ( 3; 0) Оу : ( 0; – 3 ) х 3 2 – 2 1 5 – 3 5 у При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются -4 13 " width="640"
0 → ветви вверх Вершина ( 1; – 4) Ох : ( – 1; 0) и ( 3; 0) Оу : ( 0; – 3 ) х 3 2 – 2 1 5 – 3 5 у При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются -4 13 " width="640"
№ 3
Постройте график функции:
a 0 → ветви вверх
Вершина ( 1; – 4)
Ох : ( – 1; 0) и ( 3; 0)
Оу : ( 0; – 3 )
х
3
2
– 2
1
5
– 3
5
у
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
-4
13

№ 3
Используя график функции,
найдите у(max) и у(min) :
1)
у(min)
у(max)
– 4
НЕТ
– 4
4
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
НЕТ
4
-4
![№ 3 Используя график функции, найдите область её значений 2) [ – 4; +∞) ( – ∞; 3 ] 1 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. ( – ∞; + ∞) -4](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img14.jpg)
№ 3
Используя график функции,
найдите область её значений
2)
[ – 4; +∞)
( – ∞; 3 ]
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
( – ∞; + ∞)
-4
![№ 3 Используя график найдите промежуток убывания ф-ции 3) ( – ∞; 1) ( – ∞; 1] 1 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. [ – 1; +∞) -4](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img15.jpg)
№ 3
Используя график найдите промежуток убывания ф-ции
3)
( – ∞; 1)
( – ∞; 1]
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
[ – 1; +∞)
-4
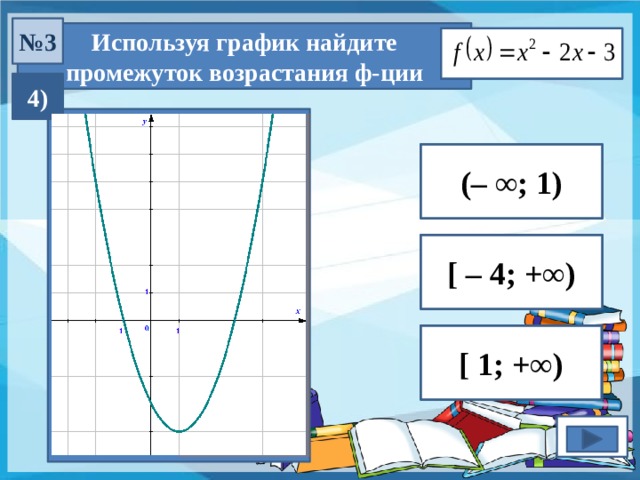
№ 3
Используя график найдите промежуток возрастания ф-ции
4)
( – ∞; 1)
[ – 4; +∞)
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
[ 1; +∞)
-4

№ 3
Используя график найдите
множество решений неравенства
5)
f ( x ) 0
– 1 ≤ x ≤ 3
– 1 x
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
– 4 0
-4
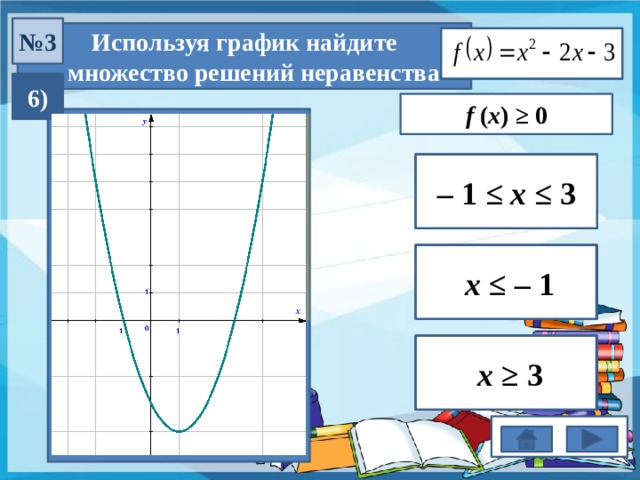
№ 3
Используя график найдите
множество решений неравенства
6)
f ( x ) ≥ 0
– 1 ≤ x ≤ 3
x ≤ – 1
1
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
x ≥ 3
-4

№ 4
Постройте график функции:
a 0 → ветви вниз
Вершина ( 1,5; 4,5)
Ох : (0; 0) и ( 3; 0)
4,5
Оу : ( 0; 0 )
х
– 1
1
2
4
у
4
– 8
При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются
1,5
20

№ 4
Используя график функции,
найдите у(max) и у(min) :
1)
у(max)
у(min)
НЕТ
0
4,5
НЕТ
3
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
4,5
4,5
![№ 4 Используя график функции, найдите область её значений 2) [ 0; 3] 4,5 ( – ∞; 1,5] На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 ( – ∞; 4,5]](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img21.jpg)
№ 4
Используя график функции,
найдите область её значений
2)
[ 0; 3]
4,5
( – ∞; 1,5]
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
( – ∞; 4,5]

№ 4
Используя график найдите промежуток убывания ф-ции
3)
[ 1,5; +∞)
4,5
( 0; 3 )
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
[ 4,5; +∞)
![№ 4 Используя график найдите промежуток возрастания ф-ции 4) ( – ∞; 4,5] 4,5 ( 0; 3 ) На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 ( –∞; 1,5]](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img23.jpg)
№ 4
Используя график найдите промежуток возрастания ф-ции
4)
( – ∞; 4,5]
4,5
( 0; 3 )
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
( –∞; 1,5]
 0 0 x 4,5 0 4,5 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 0 ≤ x ≤ 3 " width="640"
0 0 x 4,5 0 4,5 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 0 ≤ x ≤ 3 " width="640"
№ 4
Используя график найдите
множество решений неравенства
5)
f ( x ) 0
0 x
4,5
0 4,5
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
0 ≤ x ≤ 3

№ 4
Используя график найдите
множество решений неравенства
6)
f ( x ) ≤ 0
x ≤ 0
4,5
0 ≤ x ≤ 3
На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом.
1,5
x ≥ 3

Построив в одной системе координат графики функций, определите количество корней уравнения
№ 5
1)
Ответ:
3 корня
- Нажимаем на прямоугольник с уравнением.
- Для визуализации построения графиков функций нажимаем последовательно на прямоугольники с функциями
27
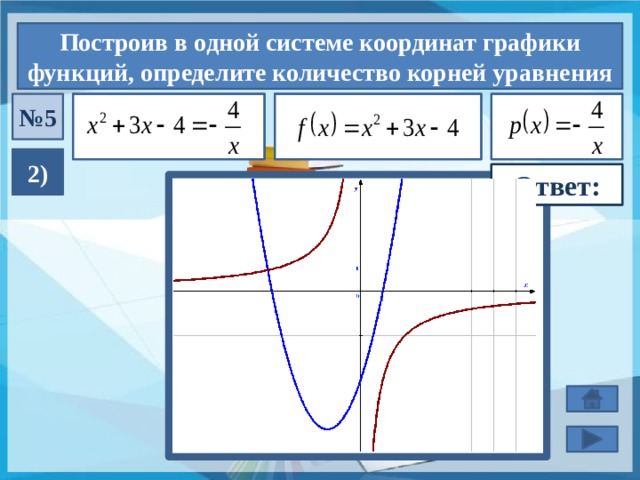
Построив в одной системе координат графики функций, определите количество корней уравнения
№ 5
2)
1 корень
Ответ:
- Нажимаем на прямоугольник с уравнением.
- Для визуализации построения графиков функций нажимаем последовательно на прямоугольники с функциями
28
 0 → ветви вверх a 0 → ветви вниз Вершина ( – 2; – 20) Вершина ( – 15; 110) Возраст. на ( – ∞; – 15] Убывает на ( – ∞; – 2] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ – 2; + ∞ ) Убывает на [ – 15; + ∞ ) 28 " width="640"
0 → ветви вверх a 0 → ветви вниз Вершина ( – 2; – 20) Вершина ( – 15; 110) Возраст. на ( – ∞; – 15] Убывает на ( – ∞; – 2] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ – 2; + ∞ ) Убывает на [ – 15; + ∞ ) 28 " width="640"
№ 6
Найдите область значений и промежутки возрастания и убывания функции:
2)
1)
a 0 → ветви вверх
a 0 → ветви вниз
Вершина ( – 2; – 20)
Вершина ( – 15; 110)
Возраст. на ( – ∞; – 15]
Убывает на ( – ∞; – 2]
Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз)
При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается.
На слайде представлено ДВА примера
Возраст. на [ – 2; + ∞ )
Убывает на [ – 15; + ∞ )
28
 0 → ветви вверх a 0 → ветви ввверх Вершина ( 2; – 7) Вершина ( – 0,8; – 3,2) Убывает на ( – ∞; 2] Убывает на ( – ∞; – 0,8] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ 2; + ∞ ) Возраст. на [ – 0,8; + ∞ ) 28 " width="640"
0 → ветви вверх a 0 → ветви ввверх Вершина ( 2; – 7) Вершина ( – 0,8; – 3,2) Убывает на ( – ∞; 2] Убывает на ( – ∞; – 0,8] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ 2; + ∞ ) Возраст. на [ – 0,8; + ∞ ) 28 " width="640"
№ 6
Найдите область значений и промежутки возрастания и убывания функции:
4)
3)
a 0 → ветви вверх
a 0 → ветви ввверх
Вершина ( 2; – 7)
Вершина ( – 0,8; – 3,2)
Убывает на ( – ∞; 2]
Убывает на ( – ∞; – 0,8]
Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз)
При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается.
На слайде представлено ДВА примера
Возраст. на [ 2; + ∞ )
Возраст. на [ – 0,8; + ∞ )
28

№ 7
При каких значениях p и q график функции проходит через точки А и В?
1)
B (– 2; 5)
A (1; – 4)
Ответ:
2)
A (1; – 1)
B ( 3; –2)
Для визуализации правильности 1) составления системы уравнений 2) результатов решения системы уравнений 3) прямоугольника с надписью «Ответ» нажимаем на прямоугольник с функций. Для визуализации окончательного ответа нажимаем на прямоугольник «Ответ»
На слайде представлено ДВА примера
Ответ:
31

№ 8
При каких значениях а и b парабола проходит через точки А и В?
1)
A (–2; 7)
B (3; – 6)
Ответ:
2)
B (–6; 26)
A (3; – 1)
Для визуализации правильности 1) составления системы уравнений 2) результатов решения системы уравнений 3) прямоугольника с надписью «Ответ» нажимаем на прямоугольник с функций. Для визуализации окончательного ответа нажимаем на прямоугольник «Ответ»
На слайде представлено ДВА примера
Ответ:
32

источники











 0 → ветви вверх 5 Вершина ( – 3; – 4) Ох : ( – 1; 0) и ( – 5; 0) Оу : ( 0; 5 ) -3 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 6 – 4 – 2 5 – 3 – 3 у -4 5 " width="640"
0 → ветви вверх 5 Вершина ( – 3; – 4) Ох : ( – 1; 0) и ( – 5; 0) Оу : ( 0; 5 ) -3 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 6 – 4 – 2 5 – 3 – 3 у -4 5 " width="640"

 0 → ветви вверх Вершина ( – 1; – 4,5) Ох : ( – 4; 0) и ( 2; 0) -1 Оу : ( 0; – 4 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 – 2 – 5 х 3,5 – 4 3,5 у -4,5 7 " width="640"
0 → ветви вверх Вершина ( – 1; – 4,5) Ох : ( – 4; 0) и ( 2; 0) -1 Оу : ( 0; – 4 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 – 2 – 5 х 3,5 – 4 3,5 у -4,5 7 " width="640"
 0 → ветви вверх Вершина ( 1; 0 ) Ох : ( 1; 0 ) Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 2 – 1 х 3 12 3 12 у 1 8 " width="640"
0 → ветви вверх Вершина ( 1; 0 ) Ох : ( 1; 0 ) Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 3 2 – 1 х 3 12 3 12 у 1 8 " width="640"
 0 → ветви вверх Вершина ( – 2; – 4) Ох : ( – 4; 0) и (0; 0) Оу : ( 0; 0 ) -2 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 0 х – 5 – 1 1 5 5 – 3 у -4 9 " width="640"
0 → ветви вверх Вершина ( – 2; – 4) Ох : ( – 4; 0) и (0; 0) Оу : ( 0; 0 ) -2 При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются 0 х – 5 – 1 1 5 5 – 3 у -4 9 " width="640"


 0 → ветви вверх Вершина ( 1; 2 ) Ох : НЕТ Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 2 2 3 3 2 6 3 11 у 1 12 " width="640"
0 → ветви вверх Вершина ( 1; 2 ) Ох : НЕТ Оу : ( 0; 3 ) При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются х – 2 2 3 3 2 6 3 11 у 1 12 " width="640"
 0 → ветви вверх Вершина ( 1; – 4) Ох : ( – 1; 0) и ( 3; 0) Оу : ( 0; – 3 ) х 3 2 – 2 1 5 – 3 5 у При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются -4 13 " width="640"
0 → ветви вверх Вершина ( 1; – 4) Ох : ( – 1; 0) и ( 3; 0) Оу : ( 0; – 3 ) х 3 2 – 2 1 5 – 3 5 у При последовательных нажатиях на прямоугольник с функцией появляются прямоугольники по алгоритму построения графика функции ( ШЕСТЬ нажатий). При нажатии на прямоугольники «Вершина», «Точки пересечения с осью Ох», «Точки пересечения с осью Оу»появляются прямоугольники-выноски на которых визуализировано решение. При повторном нажатии на эти прямоугольники выноски сворачиваются -4 13 " width="640"

![№ 3 Используя график функции, найдите область её значений 2) [ – 4; +∞) ( – ∞; 3 ] 1 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. ( – ∞; + ∞) -4](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img14.jpg)
![№ 3 Используя график найдите промежуток убывания ф-ции 3) ( – ∞; 1) ( – ∞; 1] 1 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. [ – 1; +∞) -4](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img15.jpg)





![№ 4 Используя график функции, найдите область её значений 2) [ 0; 3] 4,5 ( – ∞; 1,5] На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 ( – ∞; 4,5]](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img21.jpg)

![№ 4 Используя график найдите промежуток возрастания ф-ции 4) ( – ∞; 4,5] 4,5 ( 0; 3 ) На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 ( –∞; 1,5]](https://fsd.multiurok.ru/html/2019/11/27/s_5dde8e00f1139/img23.jpg)
 0 0 x 4,5 0 4,5 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 0 ≤ x ≤ 3 " width="640"
0 0 x 4,5 0 4,5 На этом слайде использован приём «Анимированная сорбонка». Для выбора ответа нажимаем на прямоугольник с предполагаемым ответом. 1,5 0 ≤ x ≤ 3 " width="640"



 0 → ветви вверх a 0 → ветви вниз Вершина ( – 2; – 20) Вершина ( – 15; 110) Возраст. на ( – ∞; – 15] Убывает на ( – ∞; – 2] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ – 2; + ∞ ) Убывает на [ – 15; + ∞ ) 28 " width="640"
0 → ветви вверх a 0 → ветви вниз Вершина ( – 2; – 20) Вершина ( – 15; 110) Возраст. на ( – ∞; – 15] Убывает на ( – ∞; – 2] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ – 2; + ∞ ) Убывает на [ – 15; + ∞ ) 28 " width="640"
 0 → ветви вверх a 0 → ветви ввверх Вершина ( 2; – 7) Вершина ( – 0,8; – 3,2) Убывает на ( – ∞; 2] Убывает на ( – ∞; – 0,8] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ 2; + ∞ ) Возраст. на [ – 0,8; + ∞ ) 28 " width="640"
0 → ветви вверх a 0 → ветви ввверх Вершина ( 2; – 7) Вершина ( – 0,8; – 3,2) Убывает на ( – ∞; 2] Убывает на ( – ∞; – 0,8] Для визуализации правильности решения примеров необходимо последовательно нажимать на прямоугольник с функцией (ПЯТЬ раз) При нажатии на прямоугольник «Вершина» – появляется выноска с визуализацией нахождения координат вершины параболы. При повторном нажатии выноска сворачивается. На слайде представлено ДВА примера Возраст. на [ 2; + ∞ ) Возраст. на [ – 0,8; + ∞ ) 28 " width="640"













