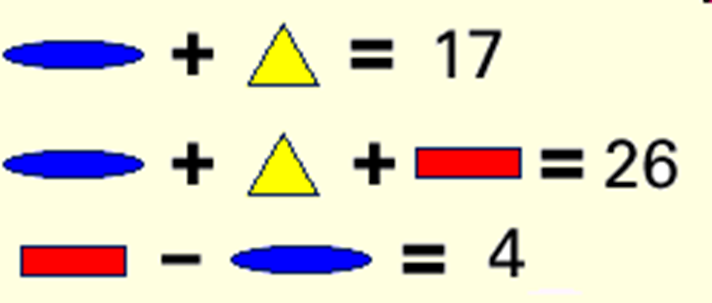Доклад по теме: «Формирование функциональной грамотности на уроках математики в начальных классах»

9

Муниципальное бюджетное общеобразовательное учреждение

Николаевская средняя общеобразовательная школа

Доклад по теме:

«Формирование функциональной грамотности

на уроках математики в начальных классах»

Выполнил:

учитель начальных классов

Грушко С.И.

.

2022г.

Формирование функциональной грамотности

на уроках математики в начальных классах.

I. До конца XIX века грамотным называли человека, умеющего читать и писать. («Толковый словарь живого великорусского языка» В.И. Даля)

В 50-е годы XX века грамотность рассматривается в качестве одного из важнейших показателей уровня социального развития государства и общества.

Современное понятие «функциональная грамотность» выходит за рамки простых умений-навыков читать - писать и постепенно начинает включать более широкие сферы общественной и культурной жизни.

Развитие функциональной грамотности вошло в ранг национальных целей и стратегических задач нашей страны. В указе Президента Российской Федерации от 7 мая 2018 года сказано, что наша страна должна стать одной из 10 ведущих стран мира по качеству образования, а в процесс обучения нужно внедрять «методики и технологии, обеспечивающие освоение обучающимися базовых навыков и умений».

Функциональная грамотность – это способность человека вступать в отношения с внешней средой и максимально быстро адаптироваться и функционировать в ней.

Мир с каждым годом становится более наполненным информацией, и детей нужно учить ориентироваться в ней.Функциональная грамотность сегодня — это базовое образование личности.

Ребенку важно обладать:

• Готовностью успешно взаимодействовать с изменяющимся окружающим миром.

• Возможностью решать различные (в том числе нестандартные) учебные и жизненные задачи.

• Способностью строить социальные отношения.

• Совокупностью рефлексивных умений, обеспечивающих оценку своей грамотности, стремление к дальнейшему образованию.

II. Виды функциональной грамотности.

1.Читательская грамотность - это способность к чтению и пониманию учебных текстов, умение извлекать информацию из текста, интерпретировать, использовать ее при решении учебных, учебно-практических задач и в повседневной жизни. Читательская грамотность – это базовый навык функциональной грамотности.

2. Математическая грамотность - это способность формулировать, применять и интерпретировать математику в разнообразных контекстах. Она включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления.

3. Естественнонаучная грамотность - это способность человека занимать активную гражданскую позицию по вопросам, связанным с естественными науками, и его готовность интересоваться естественнонаучными идеями.

4. Финансовая грамотность - это знание и понимание финансовых понятий и финансовых рисков. Включает навыки, мотивацию и уверенность, необходимые для принятия эффективных решений в разнообразных финансовых ситуациях, способствующих улучшению финансового благополучия личности и общества, а также возможности участия в экономической жизни.

5. Глобальные компетенции - это способность смотреть на мировые и межкультурные вопросы критически, с разных точек зрения, чтобы понимать, как различия между людьми влияют на восприятие, суждения и представления о себе и о других, и участвовать в открытом, адекватном и эффективном взаимодействии с другими людьми разного культурного происхождения на основе взаимного уважения к человеческому достоинству.

6. Креативное мышление - это способность продуктивно участвовать в процессе выработки, оценки и совершенствовании идей, направленных на получение инновационных и эффективных решений, и/или нового знания, и/или эффектного выражения воображения.

III. Одним из направлений функциональной грамотности является математическая грамотность.

«Математическая грамотность – это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.

Вклад математики в развитие компонентов функциональной грамотности младшего школьника очень велик. Она влияет на информационную, читательскую, социальную функциональную грамотность, информацию общекультурной направленности. Знания математики используются на уроках технологии, окружающего мира.

Математическая функциональная грамотность – это комплекс трех компонентов:

1-й компонент математической грамотности:

-ученик понимает необходимость математических знаний, чтобы решать учебные и жизненные задачи, умеет оценивать учебные ситуации, которые требуют математических знаний. Чтобы его сформировать, нужно найти ответ на вопрос ученика: «А зачем мне математика нужна?». Поэтому на уроке важный момент – проанализировать ситуацию, которая стимулирует потребность и желание изучать математику.

2-й компонент математической грамотности –

- способность устанавливать математические отношения и зависимости, работать с математической информацией: применять умственные операции, математические методы, решать геометрические задачи, связанные с жизнью, с практической деятельностью человека.

3-й компонент математической грамотности –

- владение математическими фактами (принадлежность, истинность), использование математического языка для решения учебных задач, построения математических суждений, на примере семейно-практического содержания (ремонт квартиры, оздоровление, семейные расходы).

IV.Ориентиром для нас является стандарт начального общего образования.

Цель учителя: научить учащихся добывать знания, умения, навыки и применять их в практических ситуациях, оценивая факты, явления, события и на основе полученных знаний принимать решения, действовать. Все методы, используемые педагогом, должны быть направлены на развитие познавательной, мыслительной активности, которая в свою очередь направлена на отработку, обогащение знаний каждого учащегося, на развитие его функциональной грамотности.

Наша задача сегодня через содержание учебного материала, через построение урока найти то направление, которое приведет к достижению хорошего уровня функциональной математической грамотности.

В начальной школе нужно научить решать около 40 видов различных задач. Я работаю по программе «Школа России». В учебнике много задач, связанных с реальной жизнью, особенно в 3-4 классе, когда от ребят требуется применение практических действий. Материал для задач можно брать и в окружающей нас жизни. Следовательно, такие задачи учитель может сам проектировать.

Задачи на формирование математической грамотности младших школьников я применяю на этапах – изучение нового материала, закрепление полученных знаний. Подбирая задания, отталкиваюсь от раздела и темы урока. Например, изучая раздел «Умножение и деление», больше опираюсь на 1-й компонент математической грамотности – понимание учеником необходимости математических знаний для решения учебных и жизненных задач; задачи профориентационной направленности, где предлагается помочь домохозяйке, повару-кондитеру, продавцу, и т.д., оценка разнообразных учебных ситуаций (контекстов), которые требуют применения математических знаний, умений.

2-й компонент математической грамотности использую при изучении тем «Решение геометрических задач, связанных с жизнью».

При изучении раздела «Числа больше 1000 (сложение и вычитание, умножение и деление)», я применяю 3-й компонент математической грамотности - владение математическими фактами (принадлежность, истинность), использование математического языка для решения учебных задач, построения математических суждений, на примере семейно-практического содержания (ремонт квартиры, семейные расходы).

Используемые формы работы над задачей

1. Анализ решенной задачи.

Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.

2. Решение задач различными способами.

3. Правильно организованный способ анализа задачи - от вопроса или от данных к вопросу.

4. Представление ситуации, описанной в задаче (нарисовать "картинку"). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.

Например:

-Лягушка  встречала  гостей. Лиса  пришла  раньше  Медведя, Волк  позже  Зайца, Медведь  раньше  Зайца, Сорока  позже  Волка.

Кто  пришёл  раньше  всех?  Кто  пришёл  позже  всех? В  каком  порядке  приходили  гости? (обозначь на отрезке)

) с помощью рисунка.

5. Самостоятельное составление задач учащимися.

Составить задачу:

используя слова: больше на, столько, сколько, меньше в, на столько больше, на столько меньше; решаемую в 1, 2, 3 действия;

по данному ее плану решения, действиям и ответу;

по выражению.

6. Решение задач с недостающими данными.

Задача: В первом букете ромашки. Это на 12 ромашек больше, чем во втором букете. Сколько ромашек в двух букетах?

7. Изменение вопроса задачи.

У Иры 5 роз, а у Оли на 2 розы меньше. Сколько роз у Оли?

Измени вопрос так, чтобы задача решалась в 2 действия.

8. Составление различных выражений по данным задачи и объяснение, что означает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.

9. Объяснение готового решения задачи.

10. Использование приема сравнения задач и их решений.

11. Запись двух решений на доске - одного верного и другого неверного.

12. Изменение условия задачи так, чтобы задача решалась другим действием.

И другие

VI. Нестандартные задачи.

Как показывает опыт, в младшем школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений.  

На этапе актуализации знаний, я предлагаю ребятам решить логические задачки, направленные на формирование математической грамотности. Такие задания я называю «Задачи с крючком». Решение таких задач занимает от минуты до трех минут, но я считаю, такое использование времени урока вполне рациональным, так как при этом активизируется внимание учащихся, все ребята вовлекаются в учебный процесс, они знакомятся с различными видами логических задач, тем самым пополняется запас заданий по математической грамотности.

Нестандартная задача – это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способов решения, ни того, на какой учебный материал опирается решение.

Виды нестандартных задач:

1. Логические задачи - это такие задачи, для решения которых, как правило, не требуется выполнение вычислений, а используются лишь логические рассуждения.

- задачи на переливание;

- задачи на взвешивание;

- задачи на переправы;

- задачи на разъезды;

- задачи на дележи;

- задачи на соответствие и порядок;

- истинностные задачи;

- задачи на распиливание, разрезание;

- задачи на принцип Дирихле.

2. Геометрические задачи- геометрические головоломки, геометрия в пространстве, геометрия на клетчатой бумаге.

3. Нестандартные арифметические задачи – это текстовые задачи, в которых требуется найти значение некоторой величины с помощью арифметических действий над числами и для которых в курсе математики начальной школы нет общих правил и положений, определяющих решение.

4. Комбинаторные задачи - это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа. 

5. Простейшие задачи вероятностного содержания. Это задачи на классификацию событий, задачи об исходах в испытаниях.

Методы решения нестандартных задач

• Арифметический

• Алгебраический

• Графический и практический

• Подбора

• Последовательного и упорядоченного перебора

• Метод предположения ответа

Этапы работы над задачей

1. анализ текста задачи

2. поиск решения (разбор решения и составление плана решения)

3. осуществление плана решения

4. проверка решения задачи

Приведу примеры нестандартных задач, геометрических, комбинаторных и др., ответ на которые необходимо логически обосновать:

В  клетке  находились  3 попугая. Трое  ребят  купили  по  одному  изэтих  попугаев, и  один  попугай  остался  в  клетке. Как  это  могло    случиться?

-Как  расставить  5  кубиков  в  2  ряда  так, чтобы  в  каждом  ряду  было  по  3  кубика? Нарисуй.

-На компьютере установлен пароль, состоящий из семи цифр. Цифры идут в порядке возрастания, т. е. каждая следующая цифра больше предыдущей. Вторая цифра в этом пароле — «3», пятая — «6».

 Какая цифра в пароле идёт третьей?

-Как с помощью сосудов ёмкостью 4 л и 6 л налить из водопроводного крана 2 л воды? (требует представление практических действий)

геометрические

С колько треугольников на чертеже?

12

Какая фигура имеет самое большое значение ?

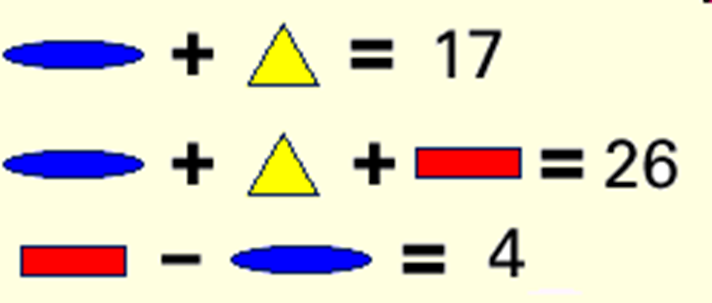
Во сколько раз один зонтик стоит дороже одного мяча, если он дороже мяча на 200 рублей?

Задачи практической направленности (их мы встречаем в впр)

-В магазине продаются бакалейные товары в упаковках. На рисунке показаны цены.

Сколько всего рублей надо заплатить за две упаковки риса и одну упаковку кукурузной крупы? Запиши решение и ответ.

Учителем составлен график пропусков уроков. Наибольшее число детей, отсутствующих на занятиях было

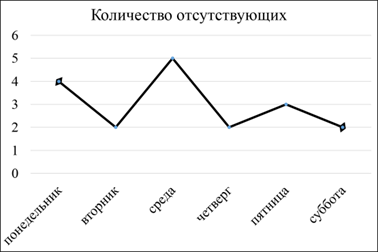
Допиши единицы измерений:

площадь школьного пенала прямоугольной формы 180…

длина дорожки 50…

площадь кухни 12…

высота окна 145…

длина гвоздя 100 …

высота дома 16…

рост школьника 1 360…

VII. Заключение

Нестандартные задачи призваны пробудить у учащихся интерес к математике.

 А заинтересованный занимательными задачами ученик начинает увлекаться математикой и переносит интерес к ней и на скучные разделы, неизбежные в каждом предмете.

В конечном счете, это способствует быстротеи глубине усвоения, прочности знаний

Свое выступление хочу закончить формулой, которая раскрывает принцип функциональной грамотности:

«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»

9