Российская Федерация, Симферополь
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 31.03.2019 15:18
Оноприенко Ольга Васильевна
Учитель математики
31 год
14 011
2 605 
Местоположение
Специализация
Доклад "Sierpinski triangle"
Категория:
Математика
25.09.2016 20:42
Просмотр содержимого документа
«Sierpinski triangle»
Ministry of Education and Science of Ukraine
V.Vernadsky Taurida National University
Sierpinski triangle
By Olga ONOPRIENKO
a second-year student
of the Mathematics department
Scientific adviser:
Galina I.Kushnereva,
Senior Lecturer,
Department of Mathematical Analysis
Language instructor:
Marina D. RYZHIKOVA,
Instructor
Simferopol
2014
Contents
Introduction ………………………………………………………………………..3
Construction ……………………………………………………………………….5
Properties…………………………..……………………………………………….8
Analogues………………………….……………………………………………….9
Conclusion……………………………………………………….……………......11
References…………………………………………………………………..…….12
Appendix…………………………………………………………………….……13
Introduction
Fractals have been known for nearly a century, are well studied and have many applications in life. The basis of this phenomenon is a very simple idea: multitude of figures can be obtained from relatively simple designs with just two operations - copying and scaling.
This concept is no strict definition. Therefore, the word "fractal" is not a mathematical term. Typically referring to the geometric shape, that satisfies one or more of the following properties:
1) a complicated structure;
2) (approximately) self-similar;
3) fractional Hausdorff (fractal) dimension which is greater than the topological one;
4) constructable by recursive procedures.
At the turn of the XIX and XX centuries, the study of fractals was rather episodic rather than systematic because earlier mathematics studied mostly "good" objects that yielded research using common methods and theories. In 1872 the German mathematician Karl Weierstrass gave an example of a continuous function which is nowhere differentiable. However, its construction was entirely abstract and difficult to understand. Therefore, in 1904 the Swede Helge von Koch invented a continuous curve, which does not have a tangent and it’s pretty easy to draw. It turned out that it has the properties of a fractal. One variant of this curve is called the " Koch snowflake”.
Frenchman Paul Pierre Levy caught the ideas of self-similarity of figures, future mentor Benoit Mandelbrot. In 1938 he published his article called "Flat and space curves and surfaces consisting of parts similar to the whole", which describes another fractal - C-curve Levy. All the facts about fractals mentioned above could be attributed to a class of design (geometric) fractals.
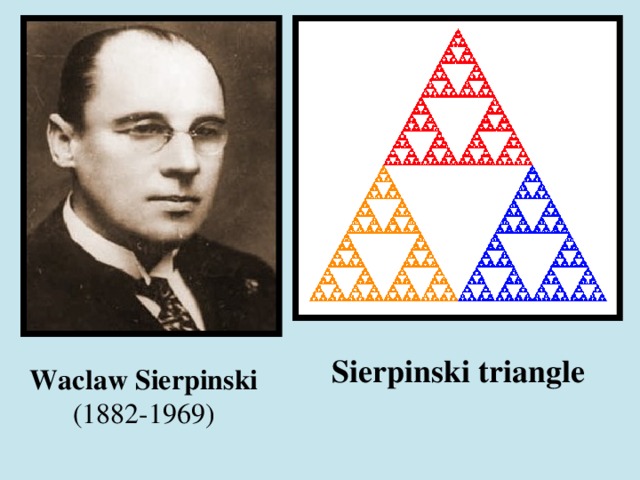
Sierpinski triangle, also called Sierpinski napkin or lattice Sierpinski, is a fractal and a fixed attractive set named after the Polish mathematician Waclaw Sierpiński who described it in 1915. However, similar patterns already appeared in the 13th-century such as Cosmati mosaics in the cathedral of Anagni, Italy, and other places, or in the nave of the Roman Basilica of Santa Maria in Cosmedin.
Originally constructed as a curve, this is one of the basic examples of self-similar sets, i.e. it is a mathematically generated pattern that can be reproducible at any magnification or reduction.
Comparing Sierpinski triangle or Sierpinski carpet to equivalent repetitive tiling arrangements, it becomes evident that similar structures can be built into any rep-tile arrangements.
Construction
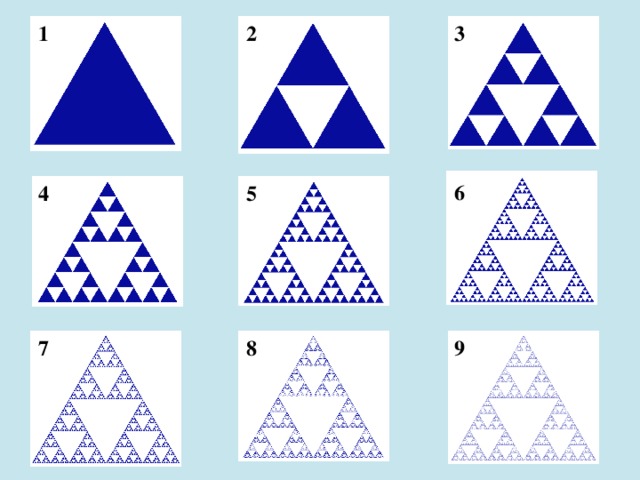
An algorithm for obtaining arbitrarily close approximations to Sierpinski triangle is as follows:
Note: each removed triangle (a trema) is topologically an open set.
Start with any triangle in a plane (any closed, bounded region in the plane will actually work). The canonical Sierpinski triangle uses an equilateral triangle with a base parallel to the horizontal axis.
Shrink the triangle to ½ height and ½ width, make three copies, and position the three shrunken triangles so that each triangle touches the two other triangles at a corner. Note the emergence of the central hole – because between them the three shrunken triangles can cover only 3/4 of the area of the original. (Holes are an important feature of Sierpinski's triangle.)
Repeat step 2 with each of the smaller triangles.
This process of recursively removing triangles is an example of a finite subdivision rule.
Note that this infinite process is not dependent upon the starting shape being a triangle—it is just clearer that way. The first few steps starting, for example, from a square also tend towards a Sierpinski triangle. Michael Barnsley used an image of a fish to illustrate this in his paper "V-variable fractals and superfractals."
The actual fractal is what would be obtained after an infinite number of iterations. More formally, one describes it in terms of functions on closed sets of points. If we let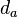 
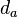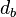note the dilation by a factor of ½ about a point a, then the Sierpinski triangle with corners a, b, and c is the fixed set of the transformation U 
U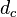 
.
This is an attractive fixed set, thus when the operation is applied to any other set repeatedly, the images converge on Sierpinski triangle. This is what is happening with the triangle above, but any other set would suffice.
If one takes a point and applies each of the transformations 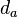, , 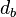and 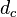to it randomly, the resulting points will be dense in Sierpinski triangle, so the following algorithm will again generate arbitrarily close approximations to it:
Start by labeling p1, p2 and p3 as the corners of Sierpinski triangle, and a random point v1. Set vn+1 = ½ ( vn + prn ), where rn is a random number 1, 2 or 3. Draw the points v1 to v∞. If the first point v1 was a point on the Sierpiński triangle, then all the points vn lie on Sierpinski triangle. If the first point v1 to lie within the perimeter of the triangle is not a point on Sierpinski triangle, none of the points vn will lie on Sierpinski triangle, however they will converge on the triangle. If v1 is outside the triangle, the only way vn will land on the actual triangle, is if vn is on what would be part of the triangle, if the triangle was infinitely large.
Or more simply:
Take 3 points in a plane to form a triangle, you need not draw it.
Randomly select any point inside the triangle and consider that your current position.
Randomly select any one of the 3 vertex points.
Move half the distance from your current position to the selected vertex.
Plot the current position.
Repeat from step 3.
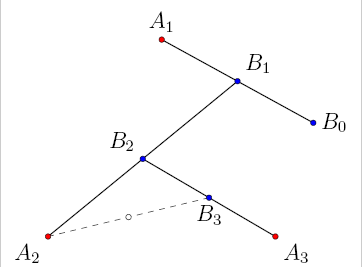
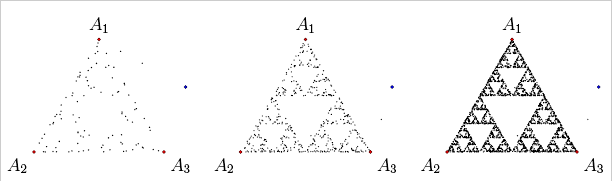
Note: This method is also called the Chaos game. You can start from any point outside or inside the triangle, and it would eventually form Sierpinski triangle with a few leftover points. It is interesting to do this with pencil and paper. A brief outline is formed after placing approximately one hundred points, and detail begins to appear after a few hundred.
Properties
For integer of dimensions d, when doubling a side of an object, 2 d copies of it are created, i.e. 2 copies for 1 dimensional object, 4 copies for 2 dimensional object and 8 copies for 3 dimensional object. For Sierpinski triangle doubling its side creates 3 copies of itself. Thus, Sierpinski triangle has Hausdorff dimension log(3)/log(2) ≈ 1.585 which follows from solving 2 d = 3 for d.
The area of a Sierpinski triangle equals zero (in Lebesgue measure). The area remaining after each iteration is clearly 3/4 of the area from the previous iteration, and an infinite number of iterations results in zero.
The points of a Sierpinski triangle have a simple characterization in Barycentric coordinates.
If a point has coordinates (0.u1u2u3…,0.v1v2v3…,0.w1w2w3…) expressed as Binary numbers, then the point is in Sierpinski's triangle if and only if ui+vi+wi=1 for all i.
Analogues
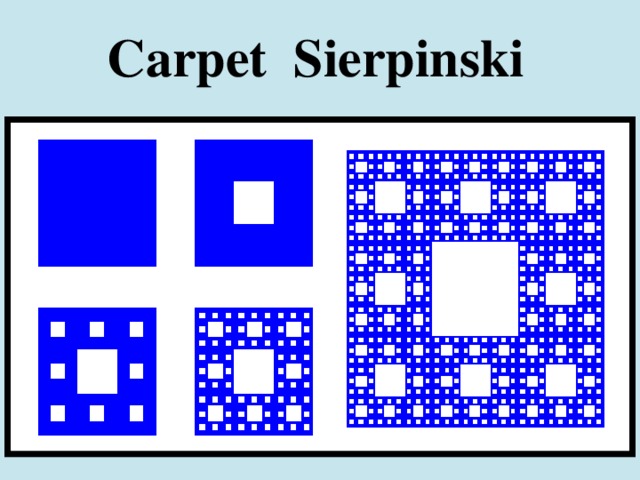
Carpet (square, napkin) Sierpinski. Square version was described by Waclav Sierpinski in 1916. He managed to prove that any curve, which can be drawn on the plane without self intersections, is homeomorphic to some subset of the holey square. As a triangle, a square may be produced from different constructions. Below is shown: according to it you have to split the square into 9 pieces and discarding the middle part. Then, the same is repeated for the remaining eight squares, etc.
Like the Triangle the square has a zero area. The fractal dimension of Sierpinski carpet is log38, calculated in a similar dimension of the triangle.
Sierpinski Pyramid is one of the three-dimensional analogues of Sierpinski triangle. Constructed in a similar way, but in three-dimensional space: 5 copies of the initial pyramid compressed twice, constitute the first iteration, that will make 5 copies of the second iteration, etc. The fractal dimension is equal to log25. The figure has a zero volume (at each step half the volume ejected), but saved the area surface of each iteration.
Menger sponge is a generalization of Sierpinski triangle in three-dimensional space. To build a sponge, you need an infinite repetition of the procedure: each of the cubes, making up the iteration, is divided into 27 three times smaller cubes, of which central and his 6 neighbors are discarded. That is, each cube generates 20 new, three times smaller ones. Therefore, the fractal dimension is log320. This fractal is a universal curve: any curve in three-dimensional space is homeomorphic to a subset of the sponge. Sponge has a zero volume (since at each step, it is multiplied by 20/27), but it is an infinitely large area.
Conclusion
On the one hand geometric fractals are the subject of scientific study. On the other hand, they can "see" - even people far from mathematics can find something for themselves in them.
This combination is rare in modern mathematics, which defines all the objects using unclear words and symbols. Many geometric fractals can literally be drawn on a piece of graph paper.
All the resulting images are only finite approximations of infinite in essence fractal. But it is always possible to draw such an approximation, that an eye will not distinguish very small details, and our imagination can create a true picture of the fractal.
For example, given a large enough sheet of graph paper and a stock of spare time, you can manually draw such an accurate approximation to Sierpinski carpet, which a naked eye will see as a true fractal from a distance of several meters. The computer will save time and paper and still increase the accuracy of the drawing.
References
1. Encyclopedic Dictionary of the young mathematician. M., Pedagogy, 1989.
2. Bozhokin S.V., Parshin D.A. Fractals and multifractals.M.,Mir, 1991.
3. Kronover R.M. Fractals and chaos in dynamical systems. Fundamentals of theory.-M., Postmarket, 2000.
4. Barnsley M. V-variable fractals and superfractals.-M., Media, 2001.
Appendix
Waclaw Sierpinski
(1882-1969)
Sierpinski triangle
Просмотр содержимого документа
«_ТРЕУГОЛЬНИК_СЕРПИНСКОГО»
Просмотр содержимого презентации
«Sierpinski triangle»
Sierpinski triangle
Sierpinski triangle
Waclaw Sierpinski
(1882-1969)
Construction
"Chaos game"
100 points
500 points
2500 points
Carpet Sierpinski
Sierpinski Pyramid
Menger sponge
2
3
1
6
4
5
8
7
9
Application of fractals
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
