Министерство образования и науки Республики Бурятия
МОУ Сужинская средняя общеобразовательная школа
Кусочно - линейные функции.
Секция: алгебра и математический анализ.
Направление исследовательской работы: Функции и их графики.
Выполнил: Баданов Константин,
ученик 8а класса
Научный руководитель: Шагдуева
Светлана Климентьевна,
учитель математики
2017 год
Оглавление.
Введение. - 3 стр
Актуальность выбранного исследования.
Цель, задачи исследования.
Основная часть. - 4 стр
Историческая справка. - 4 стр
Графики и их практическая значимость. - 4 стр
Функция y = |x|. - 5 стр
Функция y = sgn x. - 5 стр
Функция y = [x]. - 6 стр
Функция y = {x}. - 6 стр
Заключение. - 9 стр
Выводы.
Литература. - 10 стр
Приложения.
Введение.
Изучая математику, мы узнаем все больше и больше различных фактов, получаем все больше и больше знаний. Без науки математики немыслимо сегодня ни прошлое, ни будущее. А сколько еще неразгаданного?! Человек в повседневной жизни всегда сталкивается с математикой: с числами, с законами, с функциями и поэтому тема моей исследовательской работы является актуальной и всегда останется таковой.
Графический способ – один из самых удобных и наглядных способов представления и анализа информации. Он зародился с возникновением понятия «функция», которое уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны.
Одно из основных назначений функций – описание реальных процессов, происходящих в природе. Но издавна ученые-философы и естествоиспытатели выделяли два типа протекания этих процессов: постепенное (непрерывное) и скачкообразное. Чтобы показать разрывные процессы, были введены кусочно-элементарные функции.
Гипотеза: большинство учеников и не подозревают, что есть функции, называемые линейными сплайнами.
Цель: исследовать кусочно-линейные функции, их свойства и графики.
Задачи: - проанализировать специальную литературу по математике;
- изучить различные кусочно-линейные функции, их свойства и графики;
- провести работу с одноклассниками на основании исследования.
Объект исследования: функции и функциональные зависимости.
Предмет исследования: кусочно-линейные функции.
Методы исследования: - эмпирические: изучение литературы по теме;
- теоретические: анализ, сравнение и моделирование; формирование гипотезы.
Основная часть.
Графический способ – один из самых удобных и наглядных способов представления и анализа информации. Он зародился с возникновением понятия «функция», которое уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны.
Исследование общих зависимостей началось в 14 веке. Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им «линией интенсивностей» или «линией верхнего края». Понятие переменной величины было введено в науку французским философом и математиком Рене Декартом. Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин. Он разрушил пропасть, лежавшую со времен древнегреческой математики, между геометрией и арифметикой при записи зависимостей между величинами Декарт стал применять буквы.
Графическое изображение функции имеет большое значение для ее изучения. Метеорологическая служба фиксирует изменения температуры, строя с помощью термографа график температуры. Используя показания сейсмографов, геологи могут предсказывать приближение землетрясения или цунами. Врачи выявляют болезни сердца. Изучая графики, полученные с помощью кардиографа, их называют кардиограммами. Широко применяются графики в экономике, в частности кривая спроса и предложения, линия производственных возможностей.
Функции «сигнум x», «антье от x» и «дробная часть x» на уроках алгебры не изучаются. Но меня эти функции заинтересовали после того, как мы рассмотрели на уроке функцию y = |x|. Я обратился к учителю математики с вопросом: «А существуют ли еще функции, графики которых состоят из прямых, лучей или отрезков?» Тогда мне преподаватель дала дополнительный материал, который на уроках мы не рассматриваем. И я начал свое небольшое исследование.
Внимательное рассмотрение определений названых функций и их графиков позволяет заметить, что все они являются кусочно-линейными, то есть заданными линейно (в виде различных линейных зависимостей) на различных промежутках области определения. Это и упрощает, и затрудняет их изучение. Облегчает потому, что технически построить графики достаточно просто. Затрудняет, так как привычное построение графиков по точкам приводит к серьезным и частым ошибкам, являющимся следствием различного задания функции на различных промежутках области определения.
Функция y = |x|.
Понятие модуля числа известно нам еще из курса математики 6 класса, когда мы начали изучать целые числа.
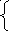 х, если х ≥ 0,
х, если х ≥ 0,
y = |x| =
- х, если х
Однако не все ученики сознательно усваивают это понятие. Поэтому перед изучением функции y = |x| мы выполняли некоторые упражнения, которые помогли нам восстановить и лучше осознать понятие модуля.
Из определения модуля видно, что функция y = |x| различно задается для неотрицательных и отрицательных значений аргумента, хотя на каждом из этих множеств она задана линейно: y = x, если x ≥ 0, и y = - x, если x
Область определения: R
Функция y = |x| является четной
Множество значений функции: [0; +∞), то есть функция неотрицательна.
Функция y = |x| убывает при отрицательных значениях, возрастает при неотрицательных значениях x
Графиком является биссектриса 2-ого координатного угла при x x ≥ 0. В точке x = 0 график функции как бы «переломлен». Особенности функции y = |x| заключаются в том, что построение ее графика выполняется не «по точкам», а по определению и свойствам, из него вытекающим. Это относится и к другим кусочно-линейным функциям.
Функция y = sgn x.
У обеих функций y = |x| и y = sgn x имеется только одно значение переменной (аргумента), при котором меняется поведение функции. Кроме того, графически обе функции изображаются «похоже»: двумя лучами и точкой между ними. Только функция «модуль» непрерывна, а функция «сигнум» в точке x = 0 имеет разрыв.
Н азвание функции «сигнум» происходит от латинского «signum» и переводится знак. Таким образом, функции «модуль x» и «сигнум x» являются характеристиками действительно числа.
азвание функции «сигнум» происходит от латинского «signum» и переводится знак. Таким образом, функции «модуль x» и «сигнум x» являются характеристиками действительно числа.
Определение: 1, если х 0,
sgn x = 0, если х = 0,
- 1, если х
Из определения следует некоторые свойства функции:
Область определения – множество R.
Множество значений состоит из трех чисел y = {-1; 0; 1}.
Функция постоянна при x x 0
Функция нечетная: sgn (-x) = - sgn x. График функции строится по определению.
Функцию «сигнум» ввел Л. Кронекер в 1878 г. И еще один интересный факт. Оказывается, что |x| = x · sgn x, а x = |x| · sgn x.
Функция y = [x].
Определение. Антье от x (целая часть x) есть наибольшее целое число, не превосходящие x.
В определении надо выделить два слова: «наибольшее» и «не превосходящее. Пояснить можно примерами. Термин «антье» происходит от французского «entire» - целый, обозначение [x] ввел К.Гаусс в 1808 году.
Из определения сразу вытекают основные свойства функции «антье»:
Область определения: R.
Множество значений: Z.
Функция является кусочно-постоянной, на каждом промежутке [k; k+1), k Є Z, функция принимает одно значение k. Поэтому функция неубывающая, то есть для любых х2 ≥ х1 имеет место неравенство [x2] ≥ [x1]. Поэтому же при х y= 0 при х = 0 и y ≥ 0 при х 0.
Следует отметить и некоторые специальные свойства функции:
[x + n] = [x] + n, если х Є R, n Є N.
Если х не принадлежит Z, то [- x] = - [x] – 1.
При любых действительных значениях х выполняется система неравенств [x] ≤ х x] + 1. Указанные свойства используются при построении графика функции.
Хочется отметить и особенности построения и расположения графика функции y = [x].
На каждом из промежутков [k; k + 1), k Є Z, график изображается отрезком, открытым справа (точка с координатами (k + 1; k) графику функции не принадлежит. Иными словами, в каждой точке с целочисленными абсциссами функция y = [x] имеет разрыв. Таких точек «разрыва» столько же, сколько существует целых чисел, то есть «бесконечно много» (счетное множество).
График функции y = [x] состоит из отрезков прямых, параллельных оси абсцисс (на промежутке [0; 1) – отрезок оси абсцисс), образующих «лесенку», длина и высота каждой «ступеньки» которой равна 1.
Функция y = {x}.
Дробную часть числа можно определить через его целую часть: {x} = x – [x]. Поскольку целая часть x не превосходит x, то дробная часть числа всегда неотрицательна. Дробная часть целого числа равна 0.
Исходя из определения, устанавливаются свойства функции y = {x}:
Область определения: R.
Множество значений: [0;1).
Функция ограничена: 0 ≤ {x}
Для любого действительного числа x и любого натурального n выполняется равенство {x + n} = {x}. Таким образом, исследуемая функция является периодической, ее период – любое натуральное число, наименьший период 1.
На каждом промежутке [k; k +1) функция у = {x} возрастает, хотя на всей области определения возрастающей не является, она немонотонная.
Вследствие периодичности функции ее график достаточно построить на промежутке [0; 1), на остальных промежутках области определения график строим, используя периодичность функции.
Таким образом, график функции у = {x}, как и график функции у = [x], изобразится изолированными отрезками прямых на каждом промежутке [k; k+1), k Є Z, области определения. Эти отрезки геометрически представляют диагонали квадрата со стороной, длина которой равна 1 (длина каждого из отрезков [k; k + 1)). Левая крайняя точка диагонали имеет координаты (k; 0), правая крайняя точка с координатами (k+1; 1) графику функции не принадлежит. На каждом из указанных промежутков области определения графиком является отрезок прямой, параллельной прямой у = х (при k = 0 – часть прямой у = х). Следовательно, функция у = {х}, как и функция у = [х], имеет «разрыв» в каждой точке с целочисленными абсциссами.
Приложения кусочно – линейных функций достаточно разнообразны. Без модуля числа нет операций над рациональными, а значит и действительными числами. Функции «антье» и «дробная часть числа» широко используются логарифмах («антье» - целая часть логарифма или его характеристика, «дробная часть» логарифма – его мантисса). Но имеются и другие приложения. При решении текстовых задач «на движение» под скоростью понимается модуль скорости (известно, что скорость – вектор). Некоторые классы текстовых задач решаются с помощью функций у = [x] и у = {х}.
Например.
Длина полных метров в куске кабеля в 5 раз больше длины неполного метра. Какова максимально возможная длина кабеля?
Решение. Обозначим длину кабеля х (м). Тогда составляется уравнение 5{х} = [x] или {x} = [x]: 5.
Так как х Є [0; 5), то [x] Є [0; 5), поэтому [x] = 4. Тогда {х} = 0,8. Искомая длина кабеля равна 4,8 (м).
Ответ: 4,8 м.
Заключение.
В школьном курсе алгебры мы рассматриваем функции, строим их графики. На практике мы часто встречаемся с зависимостями между различными величинами не только в математике, но и в других сферах деятельности. С помощью графиков наиболее естественно отражаются функциональные зависимости одних величин от других. Поэтому я и решил еще больше узнать о функциях и графиках.
Одно из основных назначений функций – описание реальных процессов, происходящих в природе. С помощью графиков можно рисовать различные рисунки.
Вывод: В процессе изучения темы «Кусочно-линейные функции» я убедился, как важна математика в современной жизни, как она интересна и разнообразна. Графики играют одну из главных ролей в природе, на производстве, в медицине. Изучать функции и графики сложно, но интересно.
Литература.
Математический энциклопедический словарь. – М.: Советская энциклопедия. 1988.
Дереклева Н.И. Научно-исследовательская работа в школе. – М.: Вербум. 2001.
Канин Е. Начала в изучении функций. – М.: Чистые пруды. 2005.
Лисичкин В. Исследование функций. - М.: Чистые пруды. 2005.
Мордкович А.Г. Алгебра. 8 класс. Учебник для учащихся общеобразовательных школ. – М.: Мнемозина. 2014.
Приложения.
12







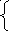 х, если х ≥ 0,
х, если х ≥ 0, азвание функции «сигнум» происходит от латинского «signum» и переводится знак. Таким образом, функции «модуль x» и «сигнум x» являются характеристиками действительно числа.
азвание функции «сигнум» происходит от латинского «signum» и переводится знак. Таким образом, функции «модуль x» и «сигнум x» являются характеристиками действительно числа. 









