Движения.Зеркальная симметрия

Мы продолжаем знакомство с движением.

На прошлом занятии вы узнали об ещё одном виде движения — осевой симметрии.

Напомню, что осевая симметрия с осью а — это отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К₁ относительно оси а.

Осевая симметрия -один из видов движения.

Отображение пространства на себя, при котором каждая точка К переходит в симметричную ей относительно плоскости β точку К₁ называется зеркальной симметрией (симметрией относительно плоскости β).

Зеркальная симметрия- отображение пространства на себя, при котором каждая точка К переходит в симметричную ей относительно плоскости β точку К₁.

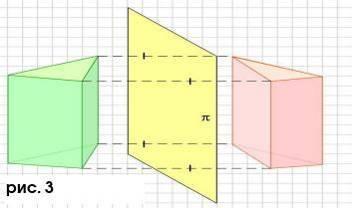
1. Введём декартову (прямоугольную) систему координат О_xyz так, чтобы плоскость О_xy совпала с плоскостью симметрии.

2. Найдем связь между точками М (x;y;z) и M₁ (x₁;y₁;z₁), которые симметричны относительно плоскости О_xy. Если точка М не принадлежит данной плоскости, то плоскость О_xy :

а) проходит через середину отрезка МM₁;

б) перпендикулярна отрезку ММ₁.

Из первого условия по формулам для координат середины отрезка имеем:

z+z₁ =0, откуда z=-z₁

2

Из второго условия следует, что отрезок МM₁ параллелен оси аппликат О_z , таким образом, x=x₁; y =y₁.

Данные формулы верны и в том случае, если точка М лежит в плоскости О_xy.

3. Рассмотрим любые две точки: А — с координатами (x₁;y₁;z₁) и В — с координатами (x₂;y₂;z₂) и докажем, что расстояние между точками А₁ и В₁, которые им симметричны, равно АВ.

Точки А₁ и В₁ имеют координаты

А₁ (x₁;y₁;-z₁) и В₁ (x₂;y₂;-z₂).

По формуле расстояний между двумя точками, найдём:

АВ=√(х₂-х₁)²+(y₂-y₁)²+(z₂+z₁)²

A₁B₁=√(-х₂-х₁)²+(-y₂-y₁)²+(-z₂+z₁)²,

Очевидно, что длина отрезка АВ равна длине отрезка A₁B₁, то есть расстояние между точками сохранено.

Таким образом, мы доказали, что зеркальная симметрия является движением.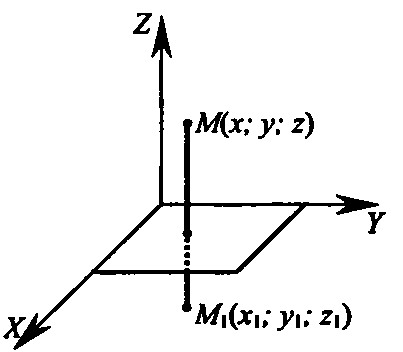

1. О_xyz-прямоугольная система координат.

О_xy -плоскость симметрии

2. Точки М(x;y;z) и M₁(x₁;y₁;z₁), симметричны относительно плоскости симметрии О_xy.

, откуда z=–z₁.

x=x₁; y =y₁.

Данные формулы верны и в том случае, если точка М лежит в плоскости О_xy.

3. А (x₁;y₁;z₁); В (x₂;y₂;z₂)

Симметричные им точки

А₁(-x₁;-y₁;-z₁) и В₁(-x₂;-y₂;-z₂).

АВ= A₁B₁=

АВ= A₁B₁

Зеркальная симметрия является движением.

Разберём несколько задач, применяя полученные знания.

Задача 1.

Доказать, что прямые а и а₁ лежат в одной плоскости, если при зеркальной симметрии прямая а отображается в прямую а₁.

Решение:

1. Введём плоскость симметрии О_xy.

Рассмотрим два случая:

- прямая а параллельна плоскости О_xy.

- прямая а не параллельна плоскости О_xy.

В случае параллельности прямой а и плоскости О_xy имеем: точки М и L, N и K симметричны (принадлежат симметричным прямым), тогда MA=AL, NB=BK.

Кроме того, все эти отрезки равны между собой: MA=AL=NB=BK, поскольку плоскость О_xy — плоскость симметрии.

Прямые МL, NK — перпендикулярны плоскости О_xy, значит МL параллельна NK (две прямые, перпендикулярные плоскости, параллельны между собой).

Таким образом, мы получили, что четырёхугольник MLKN — прямоугольник.

Поэтому прямые LK и MN параллельны как противоположные стороны прямоугольника MLKN. А значит, и прямые а и а₁, на которых лежат параллельные прямые LK и MN, будут параллельными, а значит, и лежат в одной плоскости.

Что и требовалось доказать.

2.В случае, если прямая а не параллельна плоскости О_xy, прямая а пересекает данную плоскость в точке Р.

При симметрии точка Р переходит в себя, так как лежит в плоскости симметрии О_xy.

Таким образом, точка Р принадлежит и прямой а₁.

Мы получили, что прямые а и а₁ имеют общую точку, следовательно, они лежат в одной плоскости.

Что и требовалось доказать.

Итак, мы доказали, что прямые а и а₁ всегда лежат в одной плоскости, если при зеркальной симметрии прямая а отображается в прямую а₁.

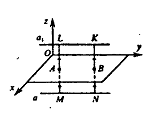
Решение:

О_xy-плоскость симметрии.

1.а║ О_xy

а и а₁-симметричны→

М и L, N и K симметричны.

MA=AL=NB=BK

МL┴ О_xy, NK┴ О_xy МL║ NK

(две прямые, перпендикулярные плоскости, параллельны между собой).

MLKN-прямоугольник

LK ║ MN а ║ а₁

а(MNL), а₁(MNL)

ч.т.д.

2.а О_xy

аО_xy=Р

РО_xy

РР

Р а₁

аа₁=Р

а(MNP), а₁(MNP)

ч.т.д.

Задача 2.

При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Доказать, что если плоскость β параллельна плоскости α, то плоскость β₁ также параллельна плоскости α.

Доказательство:

1.Выберем три точки А, В, С в плоскости β, не лежащие на одной прямой.

2.Дополнительное построение: проведём отрезки АА₂, ВВ₂, СС₂ перпендикулярно плоскости α.

Продолжим эти отрезки за точки А₁, В₁, С₁ так, что А₂А₁=АА₂, В₂В₁=ВВ₂, С₂С₁=СС₂.

Мы получили, что четырёхугольник АА₁В₁В — прямоугольник, так как АА₁=ВВ₁ и АА₁║ВВ₁(в силу симметричности плоскостей β и β₁).

3.Таким образом, А₁В₁║АВ, ВВ₁=СС₁ и ВВ₁║СС₁, значит ВВ₁С₁С — прямоугольник.

Поэтому В₁С₁║ВС.

4.Плоскость β проходит через точки А₁, В₁, С₁ и эта плоскость единственна.

5. Известно, что если пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум пересекающимся прямым (В₁А₁ и В₁С₁) другой плоскости (β₁), то эти плоскости параллельны.

Итак, мы доказали, что плоскости β и β₁ параллельны.

Дано: α-плоскость симметрии.

β→β₁ при зеркальной симметрии, β║α

Доказать:β₁║α

Доказательство:

1. А, В, С β

2.Д.п. АА₂ ┴α, ВВ₂┴ α, СС₂┴α.

А₂А₁=АА₂, В₂В₁=ВВ₂, С₂С₁=СС₂

АА₁В₁В-прямоугольник(АА₁=ВВ₁ и АА₁║ВВ₁).

3. А₁В₁║АВ, ВВ₁=СС₁ и ВВ₁║СС₁

ВВ₁С₁С-прямоугольник

В₁С₁║ВС.

4. Плоскость β проходит через точки А₁, В₁, С₁ и эта плоскость единственна.

5. β ║ β₁( по признаку параллельности плоскостей).

Ч.т.д.