
ЕГЭ 2022
математика профиль

50 вариантов
И.В. Ященко

Первый вариант

Задача №1
Найдите корень уравнения

Задача №1
Найдите корень уравнения
Решение:

Задача №1
Найдите корень уравнения
Решение:

Задача №1
Найдите корень уравнения
Решение:

Задача №1
Найдите корень уравнения
Решение:

Задача №2
Найдите корень уравнения
Решение:
Ответ: 35.

Задача №2
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4.
При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.

Задача №2
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4.
При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.
Решение:
Василий
Сергей
занят
занят
свободен
свободен
занят
свободен
занят
свободен
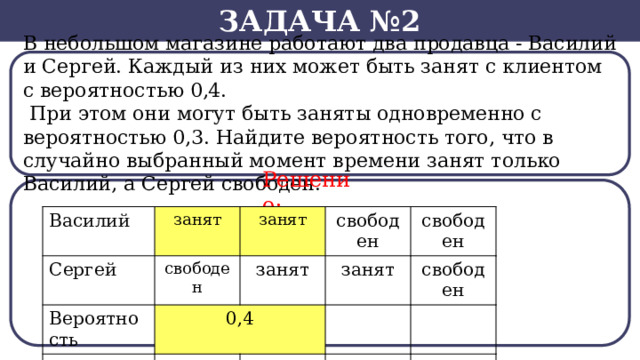
Задача №2
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4.
При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.
Решение:
Василий
Сергей
занят
Вероятность
свободен
занят
Вероятность
занят
свободен
0,4
свободен
занят
свободен
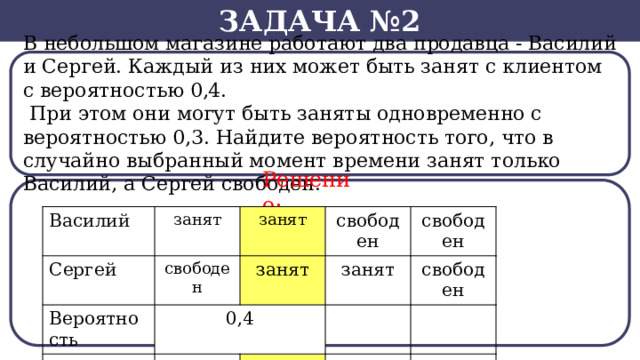
Задача №2
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4.
При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.
Решение:
Василий
Сергей
занят
Вероятность
занят
свободен
Вероятность
0,4
свободен
занят
занят
свободен
свободен
0,3
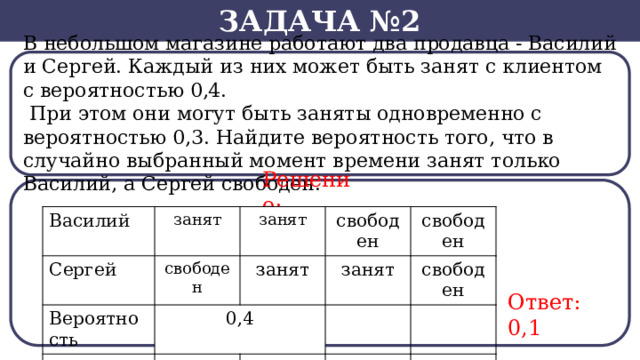
Задача №2
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4.
При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.
Решение:
Василий
Сергей
занят
Вероятность
занят
свободен
Вероятность
свободен
0,4
занят
0,1
свободен
занят
свободен
0,3
Ответ: 0,1
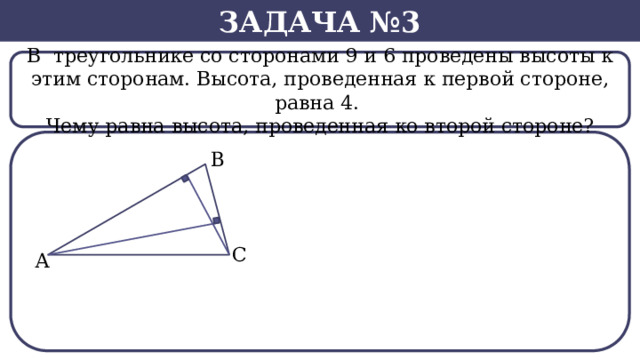
Задача №3
В треугольнике со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Задача №3
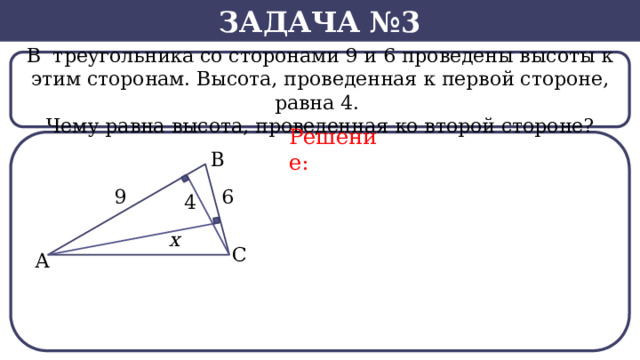
В треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Решение:
Задача №3
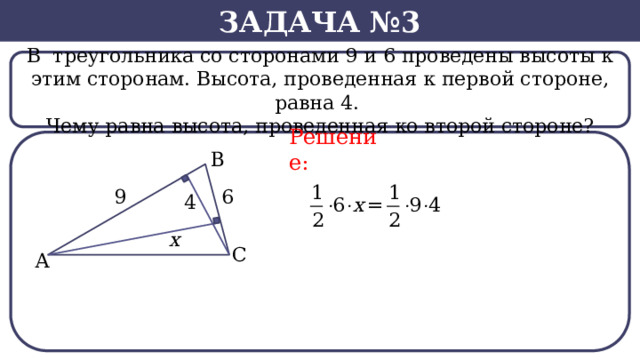
В треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Решение:
Задача №3
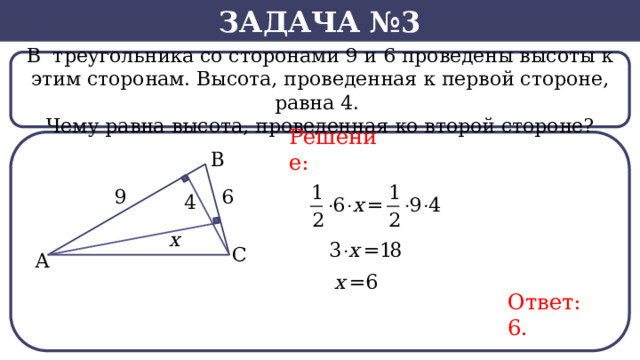
В треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Решение:
Ответ: 6.

Задача №4
Найдите значение выражения

Задача №4
Найдите значение выражения
Решение:
Ответ:3.

Задача №5
Шар вписан в цилиндр. Площадь поверхности шара равна 30.
Найдите площадь полной поверхности цилиндра.
SВ нашем случае -
Задача №5
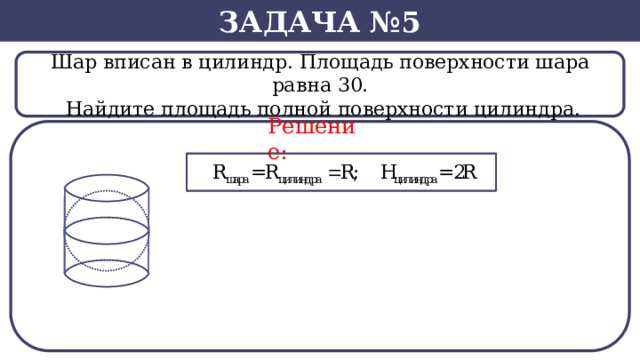
Шар вписан в цилиндр. Площадь поверхности шара равна 30.
Найдите площадь полной поверхности цилиндра.
Решение:
SВ нашем случае -

Задача №5
Шар вписан в цилиндр. Площадь поверхности шара равна 30.
Найдите площадь полной поверхности цилиндра.
Решение:
SВ нашем случае -

Задача №5
Шар вписан в цилиндр. Площадь поверхности шара равна 30.
Найдите площадь полной поверхности цилиндра.
Решение:
SВ нашем случае -
Ответ:45.
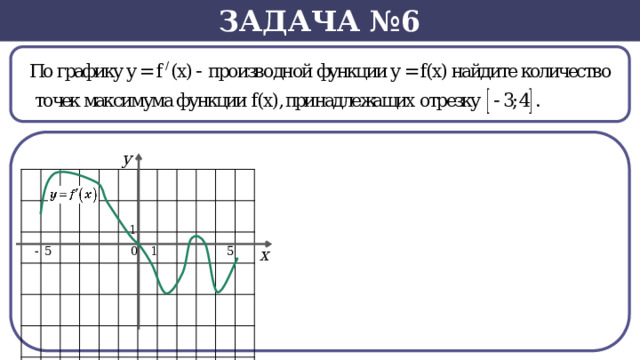
Задача №6
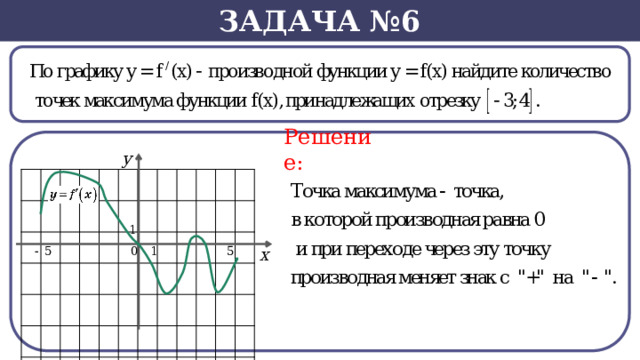
Задача №6
Решение:
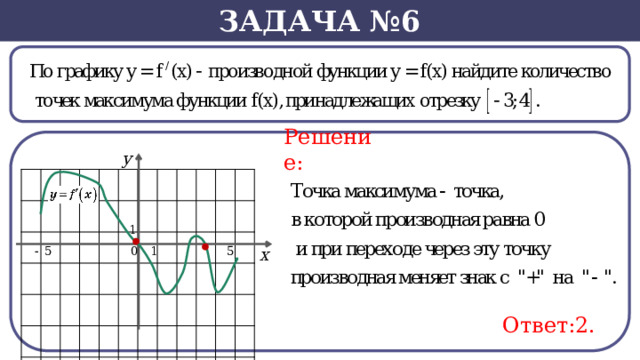
Задача №6
Решение:
Ответ:2.

Задача №7
В ходе распада радиоактивного изотопа его масса уменьшается по закону
где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.

Задача №7
В ходе распада радиоактивного изотопа его масса уменьшается по закону
где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Решение:

Задача №7
В ходе распада радиоактивного изотопа его масса уменьшается по закону
где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Решение:

Задача №7
В ходе распада радиоактивного изотопа его масса уменьшается по закону
где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Решение:

Задача №7
В ходе распада радиоактивного изотопа его масса уменьшается по закону
где m 0 — начальная масса изотопа, t — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Решение:
Ответ:30.

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:

Задача №8
Первый и второй насосы наполняют бассейн за 9 минут,
второй и третий − за 12 минут, а первый и третий − за 18 минут.
За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение:
Ответ: 8.
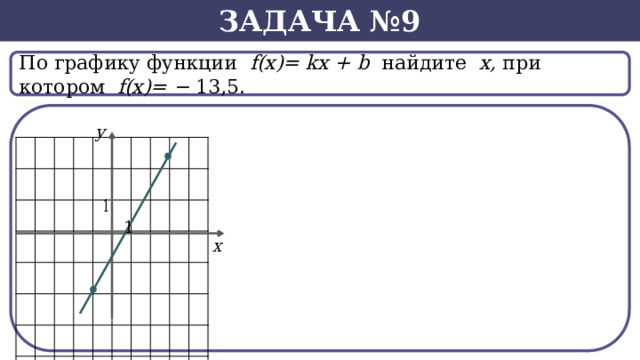
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
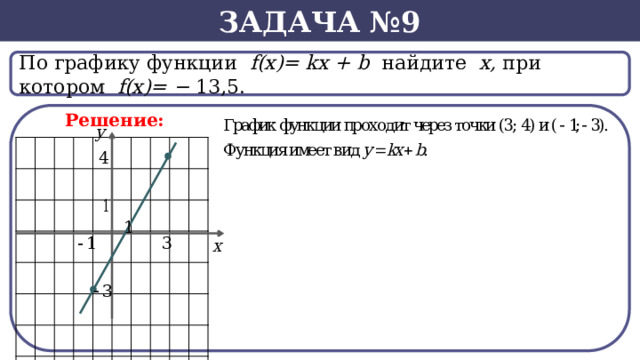
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
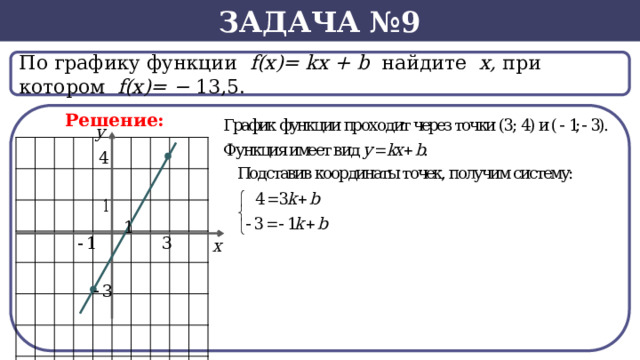
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:

Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:

Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:

Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
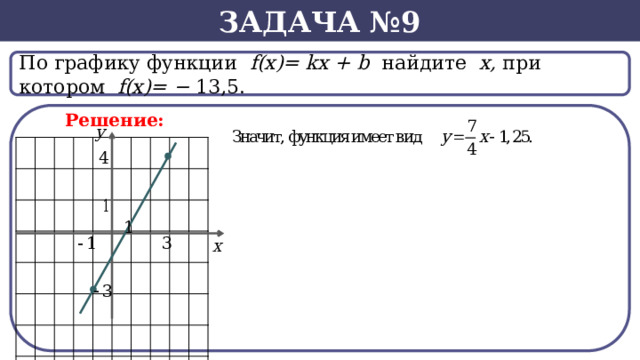
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
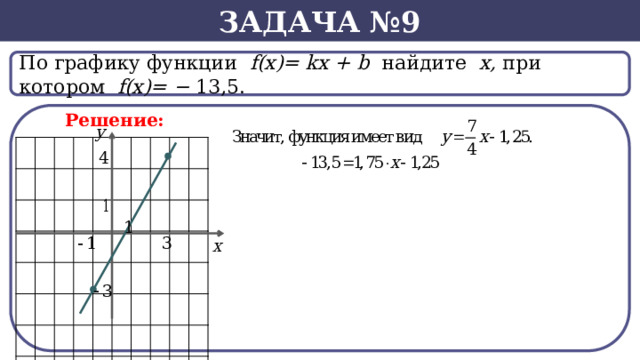
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
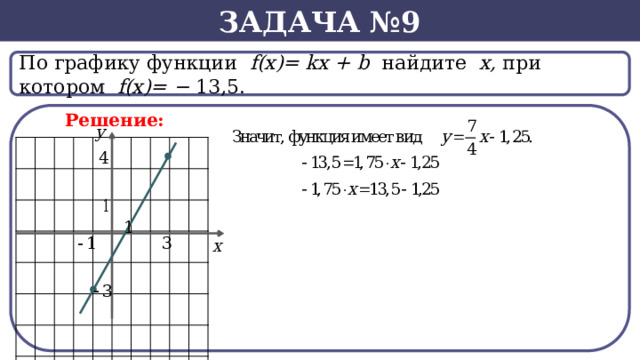
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
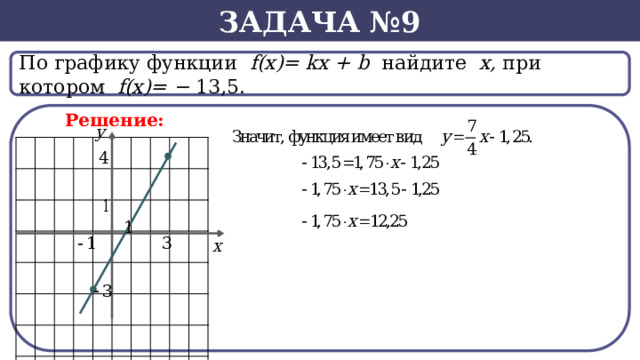
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
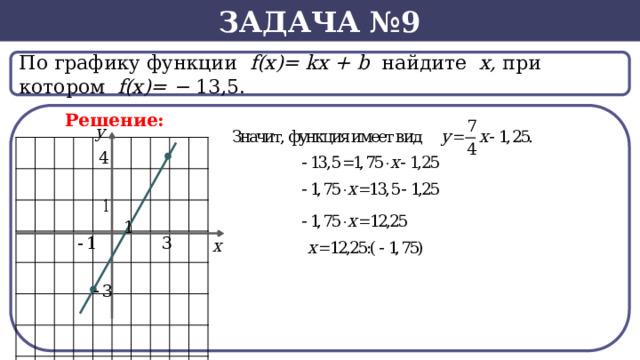
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
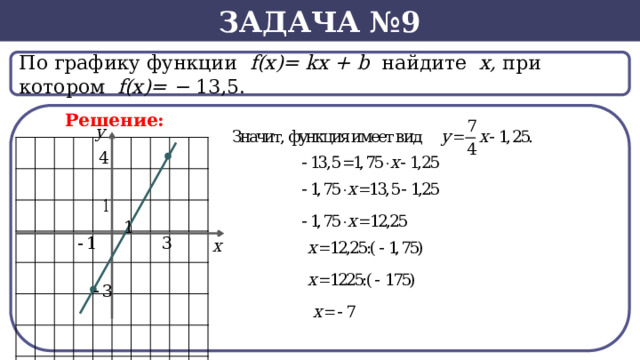
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
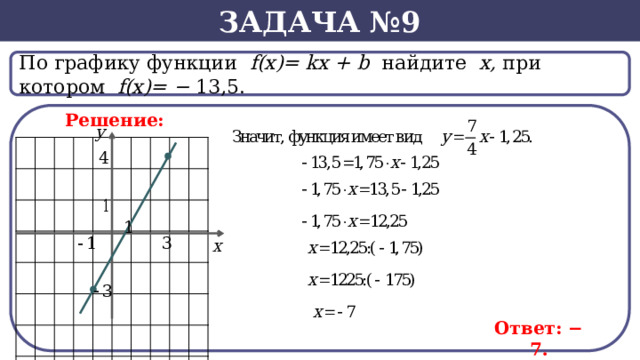
Задача №9
По графику функции f(x)= kx + b найдите х, при котором f(х)= − 13,5.
Решение:
Ответ: − 7.

Задача №10
Симметричную монету бросают 11 раз. Во сколько раз
вероятность события "выпадет ровно 5 орлов" больше
вероятности события "выпадет ровно 4 орла"?
SВ нашем случае -

Задача №10
Симметричную монету бросают 11 раз. Во сколько раз
вероятность события "выпадет ровно 5 орлов" больше
вероятности события "выпадет ровно 4 орла"?
Решение:
SВ нашем случае -

Задача №10
Симметричную монету бросают 11 раз. Во сколько раз
вероятность события "выпадет ровно 5 орлов" больше
вероятности события "выпадет ровно 4 орла"?
Решение:
SВ нашем случае -

Задача №10
Симметричную монету бросают 11 раз. Во сколько раз
вероятность события "выпадет ровно 5 орлов" больше
вероятности события "выпадет ровно 4 орла"?
Решение:
SВ нашем случае -

Задача №10
Симметричную монету бросают 11 раз. Во сколько раз
вероятность события "выпадет ровно 5 орлов" больше
вероятности события "выпадет ровно 4 орла"?
Решение:
SВ нашем случае -
Ответ: 1,4.

Задача №11
SВ нашем случае -

Задача №11
Решение:
SВ нашем случае -

Задача №11
Решение:
SВ нашем случае -

Задача №11
Решение:
SВ нашем случае -
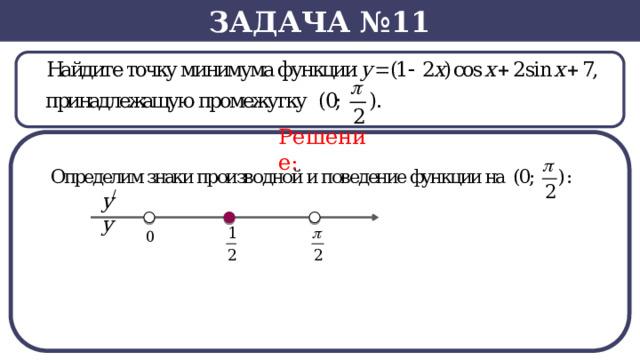
Задача №11
Решение:
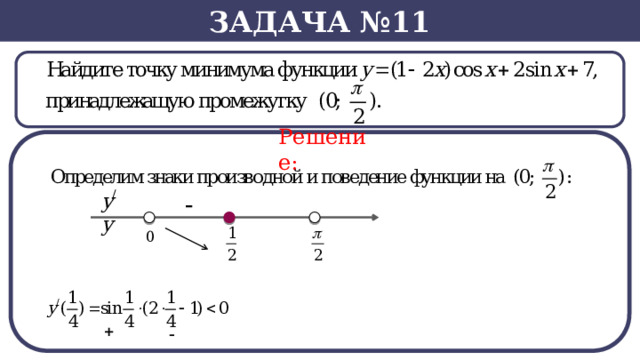
Задача №11
Решение:
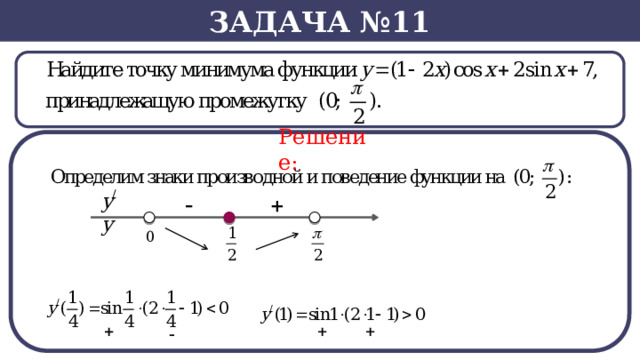
Задача №11
Решение:
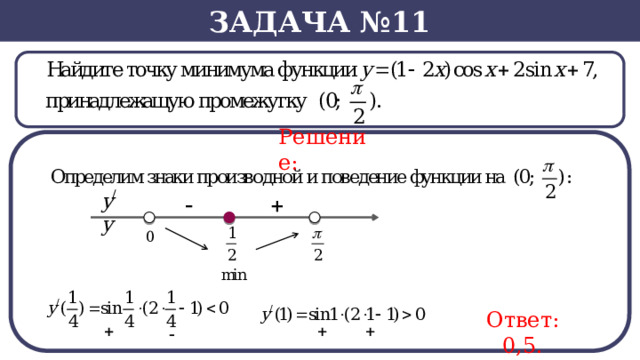
Задача №11
Решение:
Ответ: 0,5.



























































































