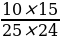ЕГЭ 2024 Вариант 7 Задание 5
В верхнем ящике стола лежит 10 белых и 15 черных одинаковых по размеру кубиков. В нижнем ящике стола лежит 15 белых и 10 черных таких же кубиков. Аня наугад взяла из верхнего ящика два кубика, а Оля — два кубика из нижнего ящика. После этого Аня положила свои кубики в нижний ящик, а Оля — в верхний. Найдите вероятность того, что в верхнем ящике по-прежнему будет 10 белых и 15 черных кубиков.
Решение:
Для того, чтобы в верхнем ящике стола ничего не изменилось, девочки должны брать одинаковые кубики. То есть Аня берет белый и белый кубики и Оля берет белый и белый кубики. Возможны три случая:
Аня и Оля берут по два белых кубика
Аня и Оля берут по два черных кубика
Аня и Оля берут по одному черному кубику и по одному синему кубику.
Теперь рассчитаем вероятность каждого случая и сложим их.
Два белых кубика
Рассчитаем вероятность того, что Аня вытащит два белых кубика из верхнего ящика. Верхний ящик содержит 10 белых и 15 черных кубиков, всего 25 кубиков. Вероятность вытащить один белый кубик равна 10/25. После того как один белый кубик был вытащен, в ящике останется 9 белых и 15 черных кубиков, всего 24 кубика. Тогда вероятность вытащить второй белый кубик равна 9/24. Вероятность того, что оба вытащенных кубика будут белыми, равна произведению этих двух вероятностей:
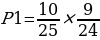
Теперь рассчитаем вероятность того, что Оля вытащит два белых кубика из нижнего ящика. В нижнем ящике 15 белых кубиков из 25, поэтому вероятность вытащить один белый кубик равна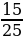 . После того как один белый кубик вытащен, в ящике остаётся 14 белых кубиков из общего количества 24 кубиков, поэтому вероятность вытащить второй белый кубик равна
. После того как один белый кубик вытащен, в ящике остаётся 14 белых кубиков из общего количества 24 кубиков, поэтому вероятность вытащить второй белый кубик равна 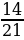 Вероятность вытащить два белых кубика подряд равна произведению этих двух вероятностей:
Вероятность вытащить два белых кубика подряд равна произведению этих двух вероятностей:
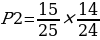
Так как Аня и Оля действуют независимо друг от друга, итоговая вероятность того, что Аня вытащит два белых и Оля два белых кубика, равна произведению вероятностей:
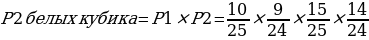
Два черных кубика
Найдем вероятность того, что Аня вытащит два черных кубика из верхнего ящика. Вероятность вытащить один черный кубик равна 15/25, а вероятность вытащить второй черный кубик будет уже 14/24. Тогда общая вероятность того, что Аня вытащит два черных кубика будет:
Р3=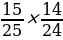
Теперь рассчитаем вероятность того, что Оля вытащит два черных кубика из нижнего ящика. Нижний ящик содержит 15 белых и 10 черных кубиков, всего 25 кубиков. Вероятность вытащить один черный кубик равна 10/25. После того как один черный кубик был вытащен, в ящике останется 15 белых и 9 черных кубиков, всего 24 кубика. Тогда вероятность вытащить второй черный кубик равна 9/24. Вероятность того, что оба вытащенных кубика будут черными, равна произведению этих двух вероятностей:
Р4=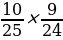
Вероятность того, что девочки вытащат по два черных кубика будет равна произведению вероятностей Р3 и Р4:
Рдва чёрных кубика=Р3*Р4=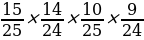
Один черный и один белый
Аня может вытащить один черный кубик и один белый двумя способами — сначала черный потом белый или сначала белый, потом черный. Вероятность события «сначала белый потом черный»:
Р5=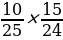
Вероятность события «сначала черный потом белый»:
Р6=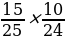
Складываем эти вероятности, так как они не могут произойти совместно:
РАня 1 чёрный 1 белый=2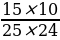
Аналогично рассуждая, находим вероятность события «Оля взяла один черный и один белый кубики»:
РОля 1 чёрный 1 белый=2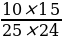
Так как события «Аня взяла черный и белый кубики» и «Оля взяла черный и белый кубики» независимы, то вероятности этих событий умножаются:
Рчёрный и белый кубики=2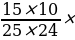 2
2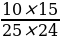
Общая вероятность
Так как мы нашли вероятности всех трех случаев и эти случаи несовместные, то для того, чтобы найти искомую вероятность, надо сложить вероятности всех трех возможных благоприятных событий:

Ответ: 0,355







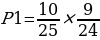
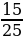 . После того как один белый кубик вытащен, в ящике остаётся 14 белых кубиков из общего количества 24 кубиков, поэтому вероятность вытащить второй белый кубик равна
. После того как один белый кубик вытащен, в ящике остаётся 14 белых кубиков из общего количества 24 кубиков, поэтому вероятность вытащить второй белый кубик равна 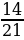 Вероятность вытащить два белых кубика подряд равна произведению этих двух вероятностей:
Вероятность вытащить два белых кубика подряд равна произведению этих двух вероятностей: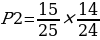
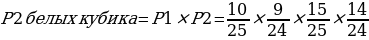
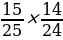
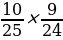
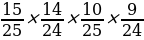
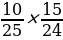
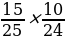
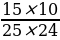
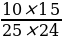
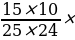 2
2