

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 19.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

ЕГЭ 2025. Март Информатика Вариант 13
1. Тип 1 № 
На рисунке справа схема дорог Н-ского района изображена в виде графа; в таблице слева содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 20 | 15 | 10 | 8 | 9 | ||
| П2 | 20 | 11 | 25 | ||||
| П3 | 5 | ||||||
| П4 | 15 | 11 | |||||
| П5 | 10 | 5 | 7 | 6 | |||
| П6 | 8 | 25 | 7 | ||||
| П7 | 9 | 6 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Д в пункт Е. В ответе запишите целое число — так, как оно указано в таблице.
2. Тип 2 № 
Логическая функция F задаётся выражением ((¬x ∨ z) ≡ (y ∧ ¬w)) → (z ∧ y). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | ||
| 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 
В файле приведён фрагмент базы данных «Мебель», принадлежащей группе компаний по производству мебели. База данных состоит из трёх связанных прямоугольных таблиц.
Таблица «Материал» содержит записи о видах материала, используемых при изготовлении мебели. Заголовок таблицы имеет вид:
| ID материала | Материал | Город | Производство |
Таблица «Продукция» содержит информацию о номенклатуре выпускаемой мебели. Заголовок таблицы имеет вид:
| ID товара | Наименование товара | Номенклатура | Номер склада | Эксплуатационное назначение |
Таблица «Готовый товар» — информацию об уже мебели. Заголовок таблицы имеет вид.
| Артикул | ID товара | ID материала | Количество на складе, шт. | Отпускная цена, руб. |
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите общую стоимость (в рублях) всех стеллажей выставочных, произведённых на предприятиях Твери из стекла.
В ответе запишите только число.
4. Тип 4 № 
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: М — 11, Л — 10, У — 001. Какое наименьшее количество двоичных знаков может содержать код слова МОЛОКО?
5. Тип 5 № 
Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 872. Суммы: 8 + 7 = 15; 7 + 2 = 9. Результат: 915.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 714.
6. Тип 6 № 
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится B начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению 6eз рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n — целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m — целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 ... КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 22 Направо 90 Вперёд 6 Направо 90]
Поднять хвост
Вперёд 1 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 9 [Вперёд 53 Направо 90 Вперёд 75 Направо 90].
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
7. Тип 7 № 
Запись о документе в информационной системе содержит его текст и отсканированную копию, полученную сканированием с разрешением 150 dpi и сжатием полученного изображения на 20%. При этом текст документа занимает 50% всего объёма записи. Сколько процентов объёма записи будет занимать текст документа, если заменить отсканированную копию на новую, сделанную с разрешением 300 dpi и сжатием изображения на 40%?
В ответе запишите только число (количество процентов), без знака %.
8. Тип 8 № 
Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква А должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Андрей?
9. Тип 9 № 
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел.
Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— в строке только одно число повторяется ровно два раза, остальные числа различны;
— среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.
10. Тип 10 № 
C помощью текстового редактора определите, сколько раз встречается сочетание букв «по» или «По» в составе других слов, включая сложные слова, соединённые дефисом, но не как отдельное слово в тексте глав XII и XIV третьей части тома 2 романа Л. Н. Толстого «Война и мир».
В ответе укажите только число.
11. Тип 11 № 
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 19 символов, каждый из которых может быть одной из 14 допустимых заглавных букв или одной из 8 цифр (цифры 0 и 3 не используются). Для записи кода на пропуске отведено минимально возможное целое число байтов. При этом используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством битов.
Код подразделения — натуральное число, не превышающее 1500, он записан на пропуске как двоичное число и занимает минимально возможное целое число байтов. Всего на пропуске хранится 36 байт данных. Сколько байтов выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байтов.
12. Тип 12 № 
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно).
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (21)
заменить (21, 5)
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка содержит десять единиц и некоторое количество двоек, других цифр нет, точный порядок расположения единиц и двоек неизвестен. После выполнения программы получилась строка с суммой цифр 34. Какое наименьшее количество двоек могло быть в исходной строке?
13. Тип 13 № 
Петя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
А
Б
В
Г
14. Тип 14 № 
Числа M и N записаны в системе счисления с основанием 9 соответственно.
M = 842x59, N = 8x7259.
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятеричной системы счисления. Определите наименьшее значение натурального числа A, при котором существует такой x, что M + A кратно N.
15. Тип 15 № 
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
ДЕЛ(120, A) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 18) → ¬ДЕЛ(x, 24)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
16. Тип 16 № 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = n + F(n − 1), если n чётно;
F(n) = 2 · F(n − 2), если n > 1 и при этом нечётно.
Чему равно значение функции F(24)?
17. Тип 17 № 
Файл содержит последовательность натуральных чисел, не превышающих 100 000. Назовём тройкой три идущих подряд элемента последовательности.
Определите количество троек, для которых выполняются следующие условия:
— ровно два числа в тройке пятизначные;
— хотя бы одно число в тройке делится на 5;
— сумма элементов тройки больше максимального элемента последовательности, запись которого заканчивается на 321. (Гарантируется, что в последовательности есть хотя бы один элемент, запись которого заканчивается на 321.) В ответе запишите два числа: сначала количество найденных троек, затем максимальную величину суммы элементов этих троек.
Ответ:
18. Тип 18 № 
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных точек может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Ответ:
19. Тип 19 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней;
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней;
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней;
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1
|
4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 
Исполнитель РазДва преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1.
2. Умножить на 2.
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя РазДва — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 62, и при этом траектория вычислений содержит число 14 и не содержит числа 59?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 4 траектория будет состоять из чисел 8, 9, 18.
24. Тип 24 № 
Текстовый файл содержит только буквы A, C, D, F, O. Определите длину самой длинной цепочки символов, которая начинается и заканчивается буквой F, а между двумя последовательными буквами F содержит не более двух букв A и произвольное количество других букв.
25. Тип 25 № 
Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Например, маске 123*4?5 соответствуют числа 123405 и 12376415.
Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1*4239?7 и при этом без остатка делятся на 3147.
В ответе запишите все найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 
В отделении банка работают два окна для обслуживания клиентов. Некоторые услуги могут быть оказаны только при обращении в определённое окно, некоторые — при обращении в любое окно. Клиент входит в отделение и встаёт в очередь к тому окну, которое оказывает необходимую ему услугу. Если услуга может быть оказана в любом окне, клиент выбирает то, в очереди к которому в данный момент меньше людей. Если очереди в оба окна одинаковые, клиент выбирает окно с меньшим номером. При этом если в очереди к выбранному окну уже стоит 14 или более человек (включая человека, которого обслуживают в данный момент), пришедший клиент сразу уходит.
Если момент завершения обслуживания одного или нескольких клиентов совпадает с моментом прихода нового клиента, то можно считать, что новый клиент пришёл после того, как обслуживание ранее пришедшего клиента завершилось и очередь сократилась.
Входные данные.
Первая строка входного файла содержит целое число N (N ≤ 1000) — общее количество клиентов, пришедших в отделение за один рабочий день. Каждая из следующих N строк описывает одного клиента и содержит 3 целых числа: время прихода клиента в отделение (количество минут с начала рабочего дня), время, необходимое для обслуживания данного клиента, и номер окна, в которое ему необходимо обратиться (0 означает, что клиент может обратиться в любое окно). Гарантируется, что никакие два клиента не приходят одновременно.
Определите, сколько клиентов будет обслужено в течение дня в окне номер 2 и сколько клиентов покинет отделение из-за слишком больших очередей.
В ответе запишите два целых числа: сначала количество клиентов, обслуженных в окне номер 2, затем количество необслуженных клиентов.
Ответ:
27. Тип 27 № 
Задание выполняется с использованием прилагаемых файлов.
По каналу связи передаётся последовательность целых чисел — показания прибора, полученные с интервалом 1 мин. в течение N мин. (N — натуральное число). Прибор измеряет значение заряда частиц, полученное регистратором за минуту, предшествующую моменту регистрации, и передаёт это значение в условных единицах измерения.
Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее мин., а их произведение было максимально возможным. В ответе запишите — найденное произведение.
Входные данные.
Даны два входных файла (файл А и файл В), каждый из которых в первой строке содержит натуральное число K — минимальное количество минут, которое должно пройти между — двумя передачами показаний, а во второй — количество переданных показаний N (1 ≤ N ≤ 10 000 000, N > K). В каждой из следующих N строк находится одно целое число, по модулю не превышающее 100 000, обозначающее числовое значение заряда частиц в минуту.
Выходные данные.
Запишите в ответе два числа: сначала значение искомой величины для файла A, затем — для файла B.
Ответ:
Просмотр содержимого документа
«ЕГЭ 2025. Март Информатика Вариант 13»
1. Тип 1 № 13349 ![]()
На рисунке справа схема дорог Н-ского района изображена в виде графа; в таблице слева содержатся сведения о протяжённости каждой из этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 20 | 15 | 10 | 8 | 9 | ||
| П2 | 20 | 11 | 25 | ||||
| П3 | 5 | ||||||
| П4 | 15 | 11 | |||||
| П5 | 10 | 5 | 7 | 6 | |||
| П6 | 8 | 25 | 7 | ||||
| П7 | 9 | 6 |
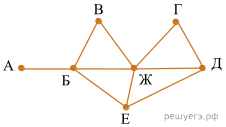
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Д в пункт Е. В ответе запишите целое число — так, как оно указано в таблице.
2. Тип 2 № 36857 ![]()
Логическая функция F задаётся выражением ((¬x ∨ z) ≡ (y ∧ ¬w)) → (z ∧ y). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | ||
| 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 58315 ![]()
В файле приведён фрагмент базы данных «Мебель», принадлежащей группе компаний по производству мебели. База данных состоит из трёх связанных прямоугольных таблиц.
Задание 3
Таблица «Материал» содержит записи о видах материала, используемых при изготовлении мебели. Заголовок таблицы имеет вид:
| ID материала | Материал | Город | Производство |
Таблица «Продукция» содержит информацию о номенклатуре выпускаемой мебели. Заголовок таблицы имеет вид:
| ID товара | Наименование товара | Номенклатура | Номер склада | Эксплуатационное назначение |
Таблица «Готовый товар» — информацию об уже мебели. Заголовок таблицы имеет вид.
| Артикул | ID товара | ID материала | Количество на складе, шт. | Отпускная цена, руб. |
На рисунке приведена схема указанной базы данных.
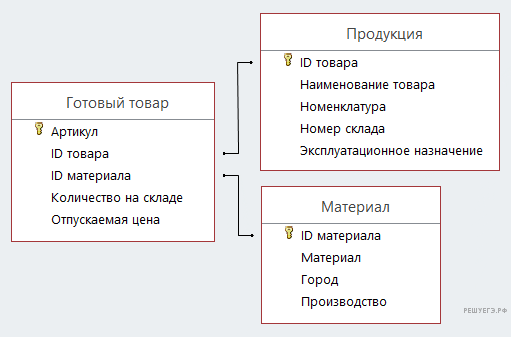
Используя информацию из приведённой базы данных, определите общую стоимость (в рублях) всех стеллажей выставочных, произведённых на предприятиях Твери из стекла.
В ответе запишите только число.
4. Тип 4 № 39233 ![]()
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: М — 11, Л — 10, У — 001. Какое наименьшее количество двоичных знаков может содержать код слова МОЛОКО?
5. Тип 5 № 14221 ![]()
Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая и вторая цифры, а также вторая и третья цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 872. Суммы: 8 + 7 = 15; 7 + 2 = 9. Результат: 915.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 714.
6. Тип 6 № 70533 ![]()
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится B начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 6 команд: Поднять хвост, означающая переход к перемещению 6eз рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n — целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m — целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 ... КомандаS] означает, что последовательность из S команд повторится k раз.
Черепахе был дан для исполнения следующий алгоритм:
Повтори 9 [Вперёд 22 Направо 90 Вперёд 6 Направо 90]
Поднять хвост
Вперёд 1 Направо 90 Вперёд 5 Налево 90
Опустить хвост
Повтори 9 [Вперёд 53 Направо 90 Вперёд 75 Направо 90].
Определите периметр области пересечения фигур, ограниченных заданными алгоритмом линиями.
7. Тип 7 № 64892 ![]()
Запись о документе в информационной системе содержит его текст и отсканированную копию, полученную сканированием с разрешением 150 dpi и сжатием полученного изображения на 20%. При этом текст документа занимает 50% всего объёма записи. Сколько процентов объёма записи будет занимать текст документа, если заменить отсканированную копию на новую, сделанную с разрешением 300 dpi и сжатием изображения на 40%?
В ответе запишите только число (количество процентов), без знака %.
8. Тип 8 № 33753 ![]()
Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква А должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Андрей?
9. Тип 9 № 47213 ![]()
Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел.
Задание 9
Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— в строке только одно число повторяется ровно два раза, остальные числа различны;
— среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.
В ответе запишите только число.
10. Тип 10 № 70537 ![]()
C помощью текстового редактора определите, сколько раз встречается сочетание букв «по» или «По» в составе других слов, включая сложные слова, соединённые дефисом, но не как отдельное слово в тексте глав XII и XIV третьей части тома 2 романа Л. Н. Толстого «Война и мир».
Задание 10
В ответе укажите только число.
11. Тип 11 № 29120 ![]()
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 19 символов, каждый из которых может быть одной из 14 допустимых заглавных букв или одной из 8 цифр (цифры 0 и 3 не используются). Для записи кода на пропуске отведено минимально возможное целое число байтов. При этом используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством битов.
Код подразделения — натуральное число, не превышающее 1500, он записан на пропуске как двоичное число и занимает минимально возможное целое число байтов. Всего на пропуске хранится 36 байт данных. Сколько байтов выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байтов.
12. Тип 12 № 28550 ![]()
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно).
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (21)
заменить (21, 5)
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка содержит десять единиц и некоторое количество двоек, других цифр нет, точный порядок расположения единиц и двоек неизвестен. После выполнения программы получилась строка с суммой цифр 34. Какое наименьшее количество двоек могло быть в исходной строке?
13. Тип 13 № 2223 ![]()
Петя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
![]()
А
![]()
Б
![]()
В
![]()
Г
14. Тип 14 № 48379 ![]()
Числа M и N записаны в системе счисления с основанием 9 соответственно.
M = 842x59, N = 8x7259.
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятеричной системы счисления. Определите наименьшее значение натурального числа A, при котором существует такой x, что M + A кратно N.
15. Тип 15 № 33485 ![]()
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
ДЕЛ(120, A) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 18) → ¬ДЕЛ(x, 24)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
16. Тип 16 № 36029 ![]()
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = n + F(n − 1), если n чётно;
F(n) = 2 · F(n − 2), если n 1 и при этом нечётно.
Чему равно значение функции F(24)?
17. Тип 17 № 63066 ![]()
Файл содержит последовательность натуральных чисел, не превышающих 100 000. Назовём тройкой три идущих подряд элемента последовательности.
Задание 17
Определите количество троек, для которых выполняются следующие условия:
— ровно два числа в тройке пятизначные;
— хотя бы одно число в тройке делится на 5;
— сумма элементов тройки больше максимального элемента последовательности, запись которого заканчивается на 321. (Гарантируется, что в последовательности есть хотя бы один элемент, запись которого заканчивается на 321.) В ответе запишите два числа: сначала количество найденных троек, затем максимальную величину суммы элементов этих троек.
Ответ:
18. Тип 18 № 60260 ![]()
Квадрат разлинован на N × N клеток (1 N
В «угловых» клетках поля — тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных точек может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута. В ответе укажите два числа — сначала максимальную сумму, затем минимальную.
18.xlsx
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Ответ:
19. Тип 19 № 27811 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней; ![]()
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 27812 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней; ![]()
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 27813 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 19 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 48.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 48 или больше камней.
В начальный момент в куче было S камней; ![]()
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, то есть не являющиеся выигрышными независимо от игры противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 47606 ![]()
В файле 22_25.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 27307 ![]()
Исполнитель РазДва преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1.
2. Умножить на 2.
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя РазДва — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 62, и при этом траектория вычислений содержит число 14 и не содержит числа 59?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 4 траектория будет состоять из чисел 8, 9, 18.
24. Тип 24 № 51993 ![]()
Текстовый файл содержит только буквы A, C, D, F, O. Определите длину самой длинной цепочки символов, которая начинается и заканчивается буквой F, а между двумя последовательными буквами F содержит не более двух букв A и произвольное количество других букв.
Задание 24
25. Тип 25 № 63074 ![]()
Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Например, маске 123*4?5 соответствуют числа 123405 и 12376415.
Найдите все натуральные числа, не превышающие 1010, которые соответствуют маске 1*4239?7 и при этом без остатка делятся на 3147.
В ответе запишите все найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 63075 ![]()
В отделении банка работают два окна для обслуживания клиентов. Некоторые услуги могут быть оказаны только при обращении в определённое окно, некоторые — при обращении в любое окно. Клиент входит в отделение и встаёт в очередь к тому окну, которое оказывает необходимую ему услугу. Если услуга может быть оказана в любом окне, клиент выбирает то, в очереди к которому в данный момент меньше людей. Если очереди в оба окна одинаковые, клиент выбирает окно с меньшим номером. При этом если в очереди к выбранному окну уже стоит 14 или более человек (включая человека, которого обслуживают в данный момент), пришедший клиент сразу уходит.
Если момент завершения обслуживания одного или нескольких клиентов совпадает с моментом прихода нового клиента, то можно считать, что новый клиент пришёл после того, как обслуживание ранее пришедшего клиента завершилось и очередь сократилась.
Задание 26
Входные данные.
Первая строка входного файла содержит целое число N (N ≤ 1000) — общее количество клиентов, пришедших в отделение за один рабочий день. Каждая из следующих N строк описывает одного клиента и содержит 3 целых числа: время прихода клиента в отделение (количество минут с начала рабочего дня), время, необходимое для обслуживания данного клиента, и номер окна, в которое ему необходимо обратиться (0 означает, что клиент может обратиться в любое окно). Гарантируется, что никакие два клиента не приходят одновременно.
Определите, сколько клиентов будет обслужено в течение дня в окне номер 2 и сколько клиентов покинет отделение из-за слишком больших очередей.
В ответе запишите два целых числа: сначала количество клиентов, обслуженных в окне номер 2, затем количество необслуженных клиентов.
Ответ:
27. Тип 27 № 59826 ![]()
Задание выполняется с использованием прилагаемых файлов.
По каналу связи передаётся последовательность целых чисел — показания прибора, полученные с интервалом 1 мин. в течение N мин. (N — натуральное число). Прибор измеряет значение заряда частиц, полученное регистратором за минуту, предшествующую моменту регистрации, и передаёт это значение в условных единицах измерения.
Определите два таких переданных числа, чтобы между моментами их передачи прошло не менее мин., а их произведение было максимально возможным. В ответе запишите — найденное произведение.
Файл А
Файл В
Входные данные.
Даны два входных файла (файл А и файл В), каждый из которых в первой строке содержит натуральное число K — минимальное количество минут, которое должно пройти между — двумя передачами показаний, а во второй — количество переданных показаний N (1 ≤ N ≤ 10 000 000, N K). В каждой из следующих N строк находится одно целое число, по модулю не превышающее 100 000, обозначающее числовое значение заряда частиц в минуту.
Выходные данные.
Запишите в ответе два числа: сначала значение искомой величины для файла A, затем — для файла B.
Ответ:
Полезное для учителя












Информатика 5 класс ФГОС
Увлекательная информатика
Информатика 2 класс ФГОС
Электронная тетрадь по информатике 7...
Информатика и ИКТ 11 класс (к учебнику...
Информатика 10 класс (Россия)
Информатика 11 класс (Беларусь)
Информатика 6 класс ФГОС
© 2025, Петриашвили Ирина Николаевна 204 1
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы