Вариант № 12
1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 февраля составляли 142 куб. м воды, а 1 марта — 156 куб. м. Сколько нужно заплатить за холодную воду за февраль, если стоимость 1 куб. м холодной воды составляет 22 руб. 50 коп.? Ответ дайте в рублях.
Решение.
Вычислим, сколько кубометров воды было израсходовано за февраль: 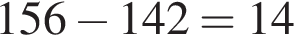 куб.м. Таким образом, необходимо заплатить:
куб.м. Таким образом, необходимо заплатить: 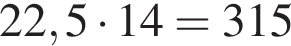 руб.
руб.
Ответ: 315
Ответ: 315
512323
315
Источник: СтатГрад: Тренировочная работа по математике 24.09.2015 вариант МА10107.
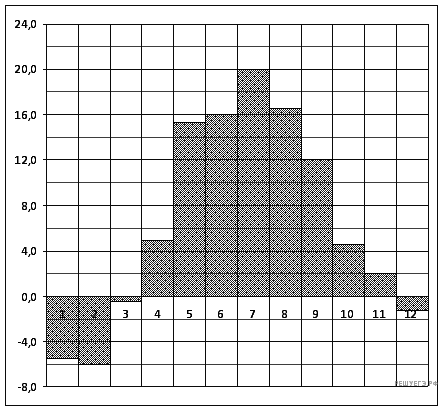
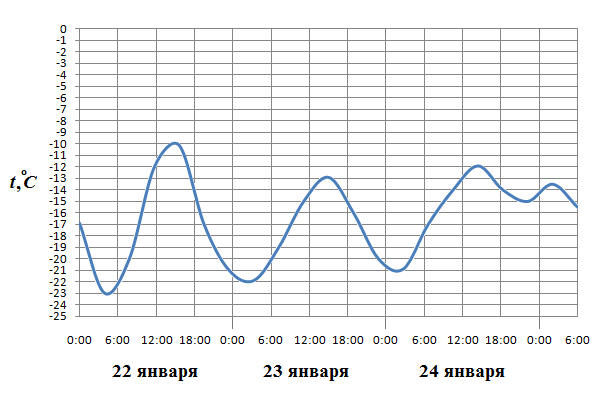
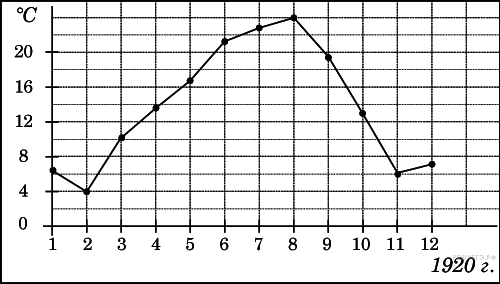
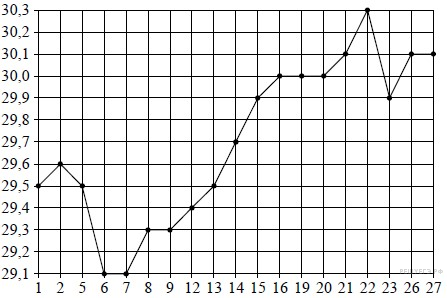
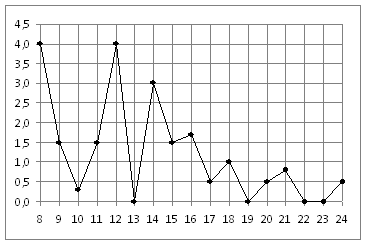
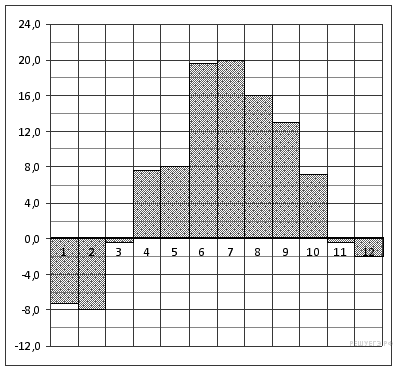
2. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведенной диаграмме, сколько месяцев среднемесячная температура не превышала 14 градусов Цельсия.
Решение.
Из диаграммы видно, что 8 месяцев среднесуточная температура не превышала 14 градусов Цельсия.
Ответ: 8.
Ответ: 8
509984
8
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
3. 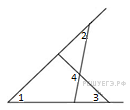 На рисунке угол 1 равен 46°, угол 2 равен 30°, угол 3 равен 44°. Найдите угол 4. Ответ дайте в градусах.
На рисунке угол 1 равен 46°, угол 2 равен 30°, угол 3 равен 44°. Найдите угол 4. Ответ дайте в градусах.
Решение.
сумма углов в выпуклом четырехугольнике равна 360°.
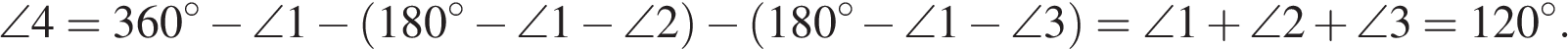
Ответ: 120.
Ответ: 120
27780
120
4. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
Решение.
Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31.
Ответ: 0,31.
Ответ: 0,31
509916
0,31
Источник: СтатГрад: Тренировочная работа по математике 22.04.2015 вариант МА10410.
5. Найдите корень уравнения 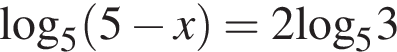 .
.
Решение.
Последовательно получаем:
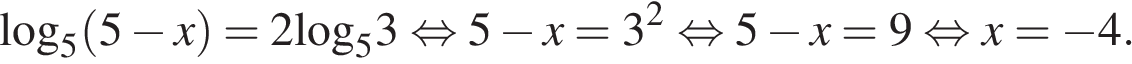
Ответ: −4.
Ответ: -4
26659
-4
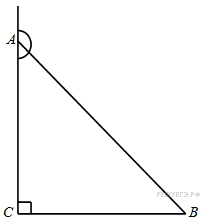
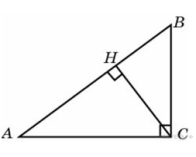
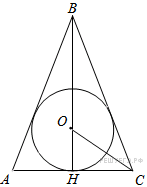
6. 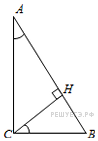 В треугольнике
В треугольнике 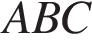 угол
угол 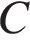 равен 90°,
равен 90°,  – высота,
– высота, 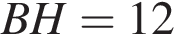 ,
, 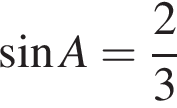 . Найдите
. Найдите 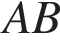 .
.
Решение.
Углы A и HCB равны как углы со взаимно перпендикулярными сторонами, поэтому
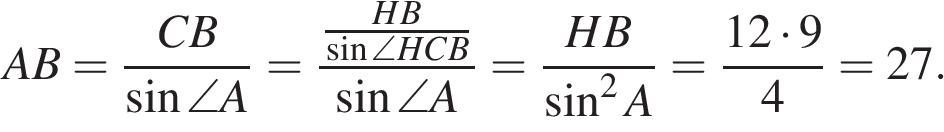
Ответ: 27.
Ответ: 27
27431
27
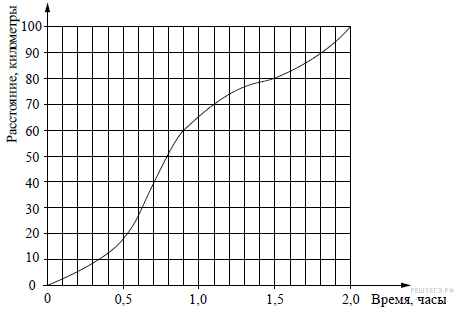
7. Материальная точка движется прямолинейно по закону 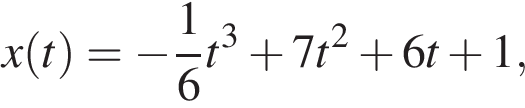 где х — расстояние от точки отсчёта (в метрах), t — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t = 6 с.
где х — расстояние от точки отсчёта (в метрах), t — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t = 6 с.
Решение.
Найдем закон изменения скорости: 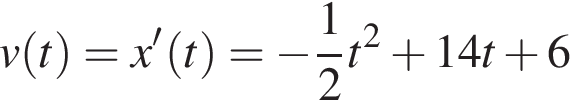 м/с. При
м/с. При  имеем:
имеем: 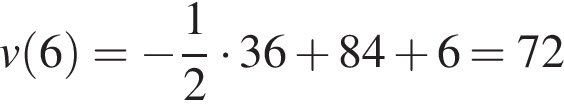 м/с.
м/с.
Ответ: 72.
Ответ: 72
512493
72
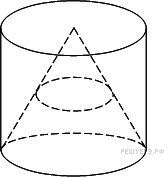
8.  Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Решение.
Площади подобных тел относятся как квадрат коэффициента подобия. Поэтому, если все ребра увеличены в 2 раза, площадь поверхности увеличится в 4 раза.
Ответ: 4.
Ответ: 4
27172
4
9. Найдите значение выражения 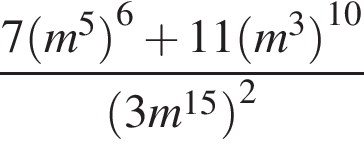 .
.
Решение.
Используем свойства степеней:
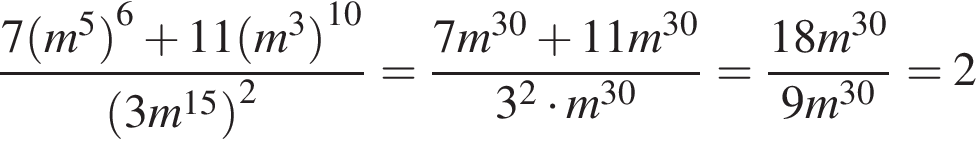 .
.
Ответ: 2.
Ответ: 2
26798
2
10. Eмкость высоковольтного конденсатора в телевизоре 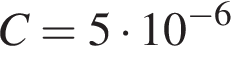 Ф. Параллельно с конденсатором подключeн резистор с сопротивлением
Ф. Параллельно с конденсатором подключeн резистор с сопротивлением 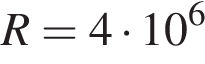 Ом. Во время работы телевизора напряжение на конденсаторе
Ом. Во время работы телевизора напряжение на конденсаторе  кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением
кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением 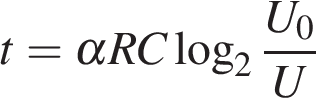 (с), где
(с), где  — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 28 с?
— постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 28 с?
Решение.
Задача сводится к решению неравенства 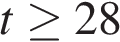 при заданных значениях начального напряжения на конденсаторе
при заданных значениях начального напряжения на конденсаторе  кВ, сопротивления резистора
кВ, сопротивления резистора 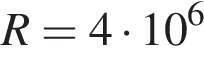 Ом и ёмкости конденсатора
Ом и ёмкости конденсатора 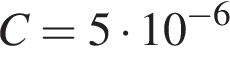 Ф:
Ф:
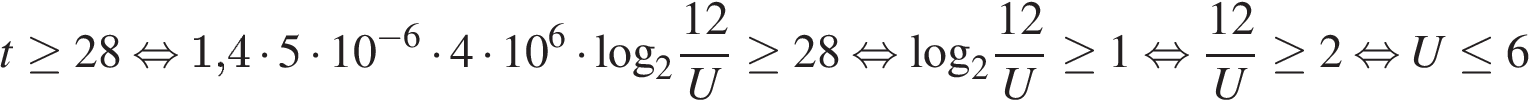 кВ.
кВ.
Ответ: 6.
Ответ: 6
28463
6
11. Из одной точки кольцевой дороги, длина которой равна 22 км, одновременно в одном направлении выехали два автомобиля. Скорость первого автомобиля равна 113 км/ч, и через 30 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение.
Пусть скорость второго автомобиля равна 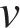 км/ч. За 1/2 часа первый автомобиль прошел на 22 км больше, чем второй, отсюда имеем
км/ч. За 1/2 часа первый автомобиль прошел на 22 км больше, чем второй, отсюда имеем
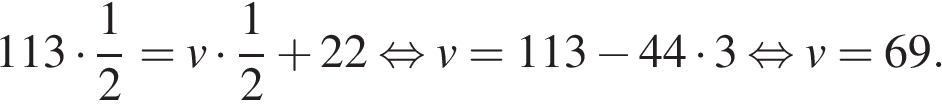
Ответ: 69.
Ответ: 69
509156
69
Источник: СтатГрад: Диагностическая работа по математике 13.02.2015 вариант МА00410.
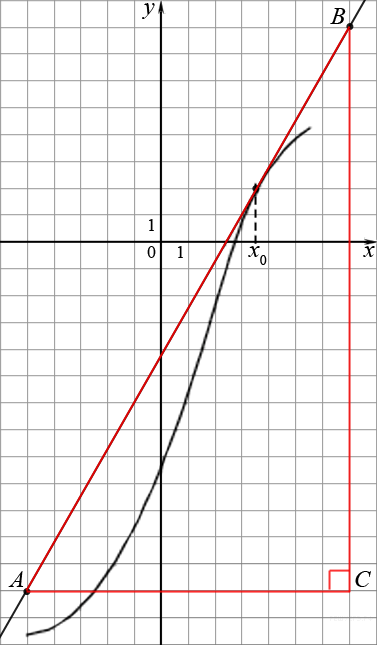
12. Найдите точку максимума функции 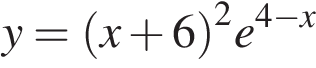 .
.
Решение.
Найдем производную заданной функции:
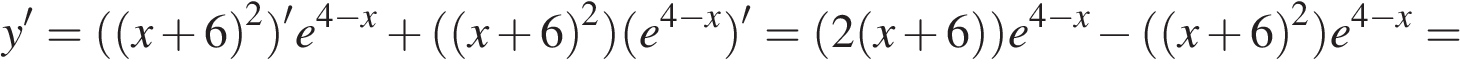
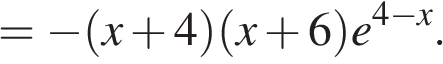
Найдем нули производной:
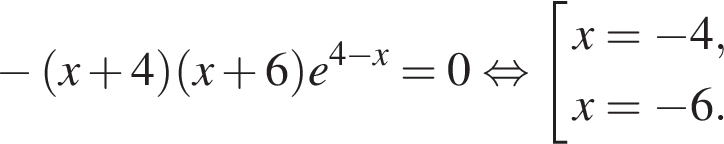
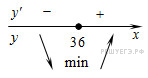
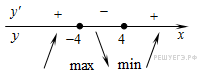
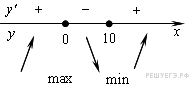
Определим знаки производной функции и изобразим на рисунке поведение функции:
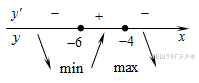
Искомая точка максимума 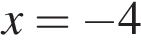 .
.
Ответ: −4.
Ответ: -4
26728
-4
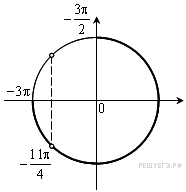
13. а) Решите уравнение
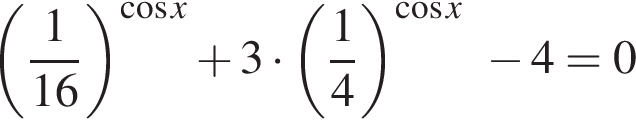
б) Найдите все корни этого уравнения, принадлежащие отрезку 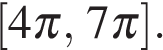
Решение.
Сделаем замену 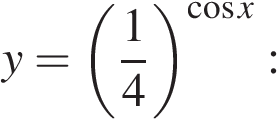
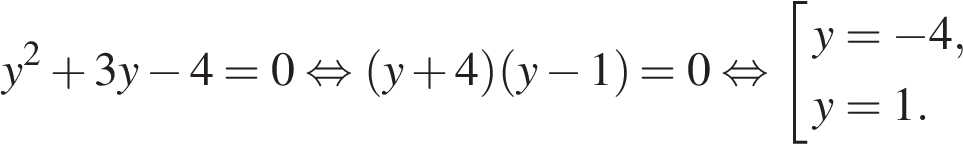 Тогда,
Тогда, 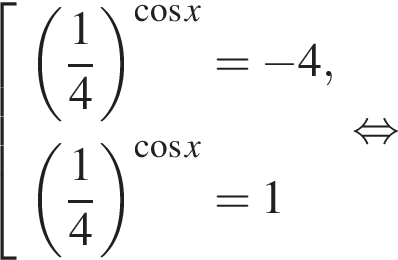
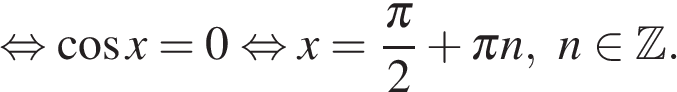
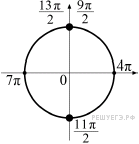 б) При помощи тригонометрической окружности отберём корни, лежащие на отрезке
б) При помощи тригонометрической окружности отберём корни, лежащие на отрезке 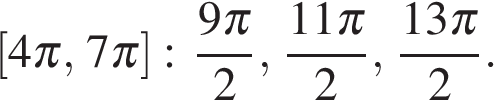
Ответ: а) 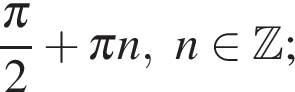 б)
б) 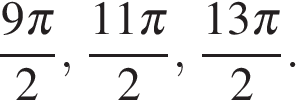
Источник: МИОО: Тренировочная работа по математике 19.05.2014 вариант МА10701.
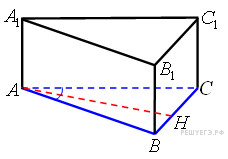
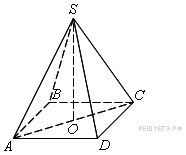
14. В треугольной пирамиде MABC с основанием ABC ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM — точка L. Известно, что AD = 2 и BE = ML = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
Сечение — треугольник  (см. рис.), найдём его стороны.
(см. рис.), найдём его стороны.
Поскольку стороны основания равны, треугольник 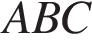 — равносторонний, следовательно, Поскольку кроме этого треугольник
— равносторонний, следовательно, Поскольку кроме этого треугольник  — равносторонний, поэтому
— равносторонний, поэтому
Треугольник прямоугольный, по теореме Пифагора:
тогда
Треугольник  прямоугольный, по теореме Пифагора:
прямоугольный, по теореме Пифагора:
Треугольники  и
и  прямоугольные,
прямоугольные,  — их общий катет, Следовательно, эти треугольники равны, поэтому равны их гипотенузы:
— их общий катет, Следовательно, эти треугольники равны, поэтому равны их гипотенузы:
Следовательно, треугольник  — равнобедренный. Проведём в нём высоту
— равнобедренный. Проведём в нём высоту  она является медианой, поэтому из треугольника
она является медианой, поэтому из треугольника  находим:
находим:
Тем самым, реугольник  — искомое сечение, найдём его площадь:
— искомое сечение, найдём его площадь:
Ответ:
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервный день. Запад. Вариант 1.
15. Решите неравенство
Решение.
Заметим, что поскольку равносильны следующие неравенства
С учётом этого имеем
Ответ:
Источник: СтатГрад: Тренировочная работа по математике 03.03.2016 вариант МА10410
16.В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
Решение.
а) Углы NAK и NBK, опирающиеся на отрезок KN, равны, значит, точки A, B, N и K лежат на одной окружности, а, следовательно, равны и вписанные углы ABK и ANK этой окружности, опирающиеся на дугу AK, что и требовалось доказать.
б) Прямоугольные треугольники KMB и NMA имеют общий угол KMN, следовательно, они подобны, откуда или но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен откуда Тогда радиус R окружности, описанной около треугольника ABM равен
Ответ: 
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
17. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Решение.
Пусть на каждый тип вклада была внесена одинаковая сумма S. На вкладе «А» каждый год сумма увеличивается на 20%, то есть умножается на коэффициент 1,2. Поэтому через три года сумма на вкладе «А» будет равна
Аналогично сумма на вкладе «Б» будет равна
где n — некоторое натуральное число.
По условию требуется найти наименьшее натуральное решение неравенства
При n = 26 неравенство
верно, а при n = 25 неравенство
неверно, как и при всех меньших n.
Ответ: 26.
Источник: СтатГрад: Тренировочная работа по математике 20.01.2016 вариант МА10310
18. Найдите все такие значения параметра a, при каждом из которых уравнение не имеет решений.
Решение.
Решение 1. Перепишем данное уравнение в виде и положим где Тогда исходное уравнение принимает вид
Найдем множество значений функции на отрезке [0; 2].
Так как то на промежутке [0; 1) и промежутке (1; 2]. Значит, функция убывает на отрезке [0; 1] и возрастает на отрезке [1; 2]. Поскольку то множество значений функции на отрезке [0; 2] ― отрезок [f (1); f (2)], т. е. отрезок Таким образом, уравнение не имеет решений на отрезке [0; 2] тогда и только тогда, когда выполняются условия или
Решение 2. Положим где и рассмотрим функцию Так как ее производная то на промежутке [0; 1) и промежутке (1; 2]. Значит, на промежутке [0; 2) функция имеет единственный экстремум ― минимум Так как уравнение не имеет решений на отрезке [0; 2] тогда и только тогда, когда выполняются условия или Таким образом, приходим к совокупности
Решение 3. Построить эскиз графика функции на отрезке [0; 2] (см. решение 1) и исследовать взаимное расположения графика этой функции и прямой
Ответ: 
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.
19. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и все их возможные суммы (по 2, по 3 и т.д.) выписывают на доске в порядке неубывания. Если какое-то число n, выписанное на доске, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 3, 6, 9, 12, 15.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 17, 18, 19, 21, 23?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 8, 9, 10, 17, 18, 19, 20, 27, 28, 29, 30, 37, 38, 39, 47.







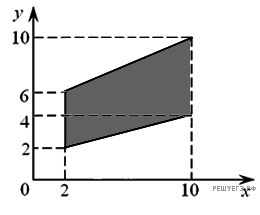 Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (10; 4), (10; 10), (2; 6).
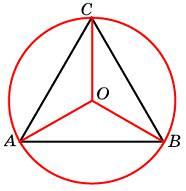
Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (10; 4), (10; 10), (2; 6).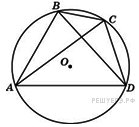 Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.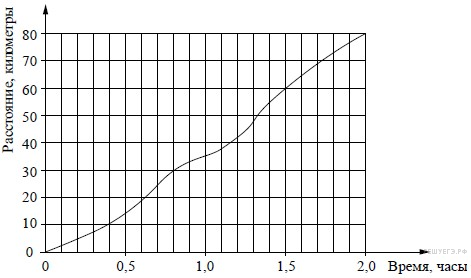
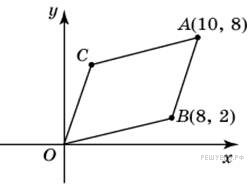 Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки
Точки O(0; 0), A(10; 8), B(8; 2) и C являются вершинами параллелограмма. Найдите ординату точки 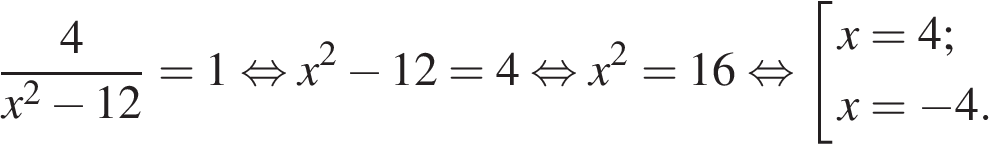

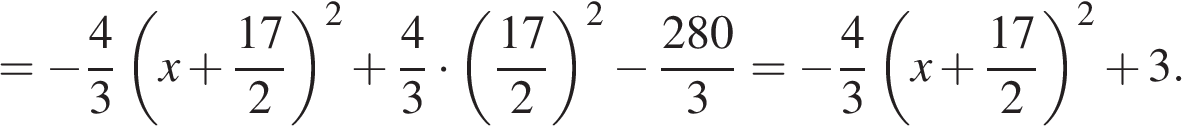
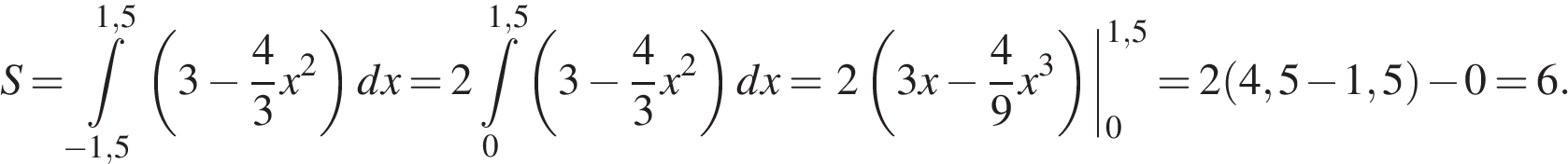
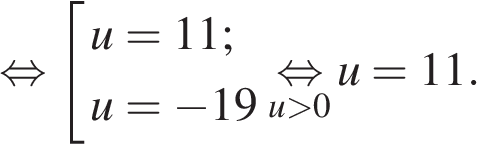
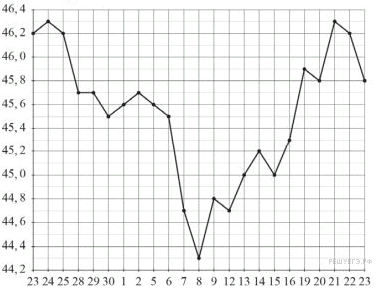
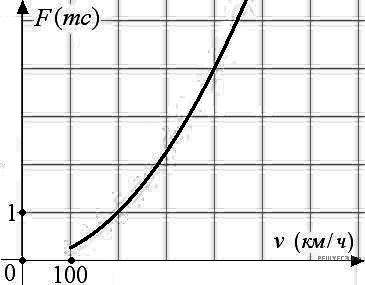 Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч? 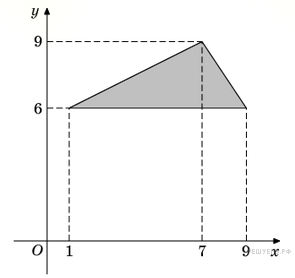 Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9).
Найдите площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9).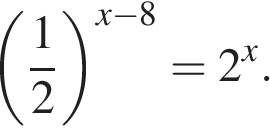
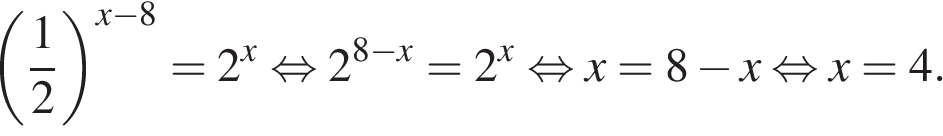
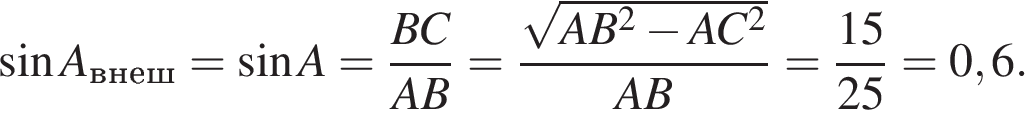
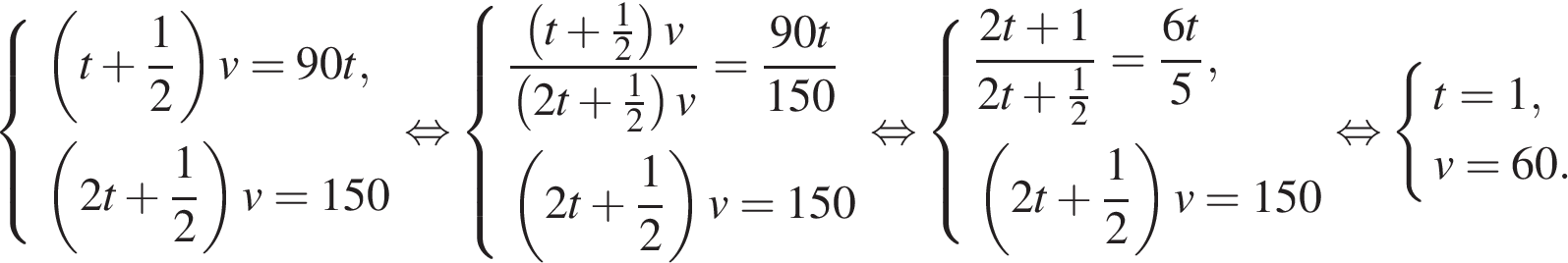

 На рисунке угол 1 равен 46°, угол 2 равен 30°, угол 3 равен 44°. Найдите угол 4. Ответ дайте в градусах.
На рисунке угол 1 равен 46°, угол 2 равен 30°, угол 3 равен 44°. Найдите угол 4. Ответ дайте в градусах. В треугольнике
В треугольнике 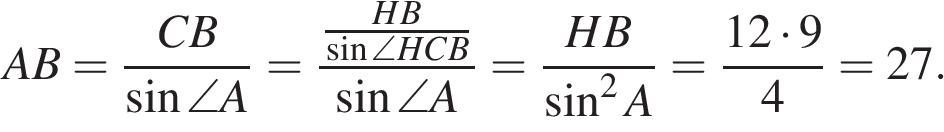
 Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?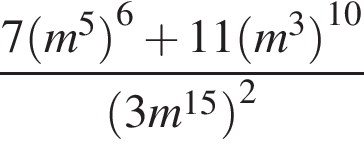 .
.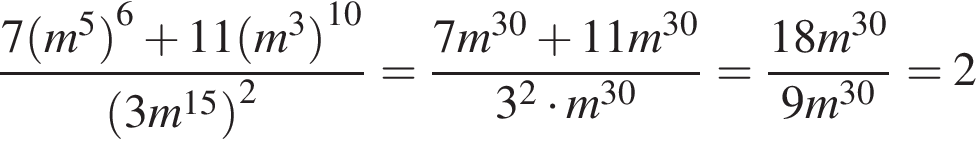
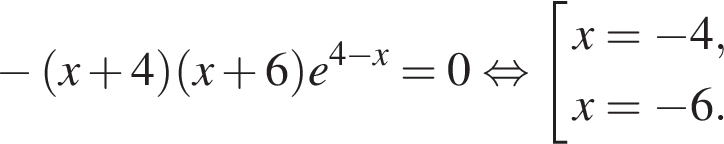
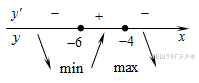
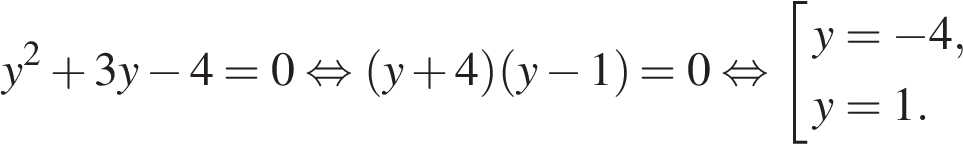
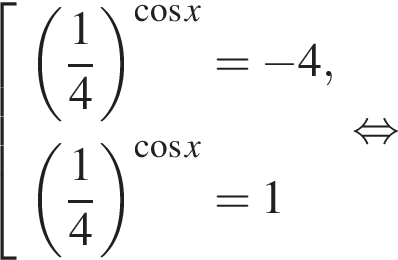

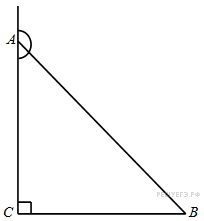 В треугольнике
В треугольнике 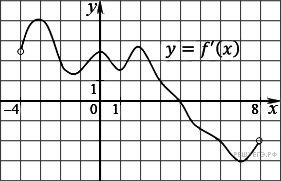 На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].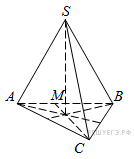
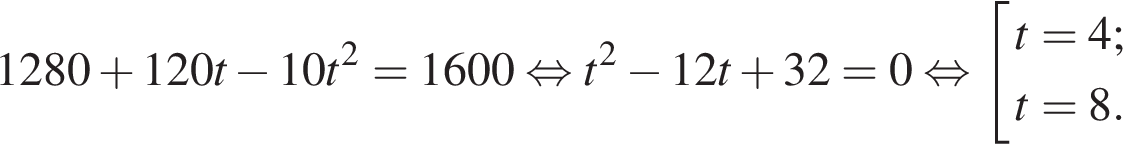
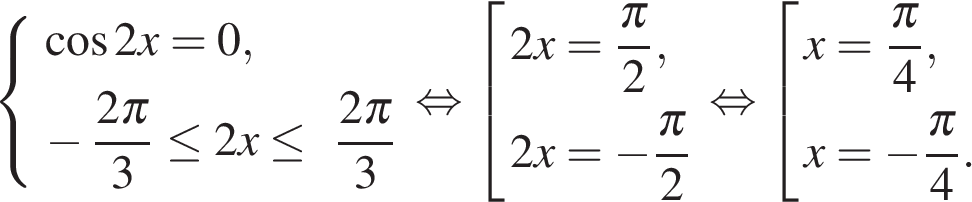
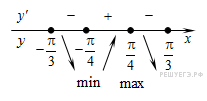
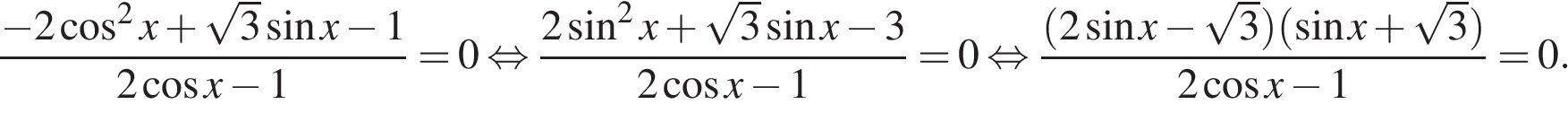
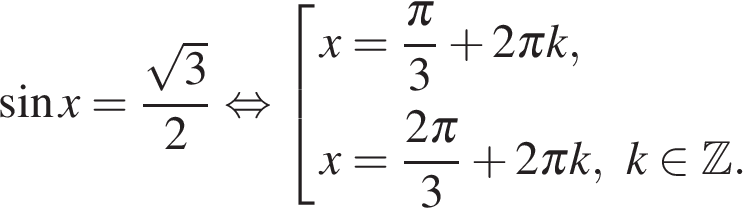
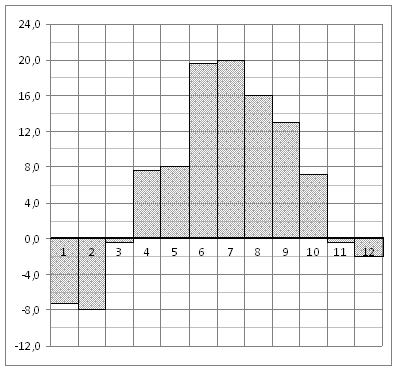
 Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 
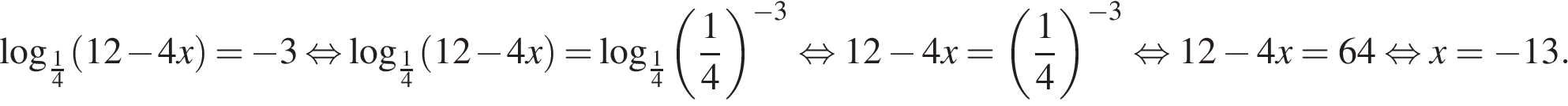
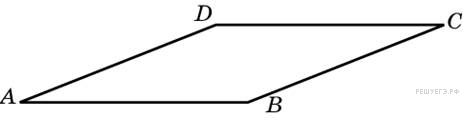
 Найдите тупой угол параллелограмма, если его острый угол равен 60°. Ответ дайте в градусах.
Найдите тупой угол параллелограмма, если его острый угол равен 60°. Ответ дайте в градусах.
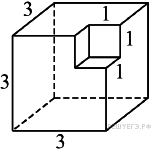 Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).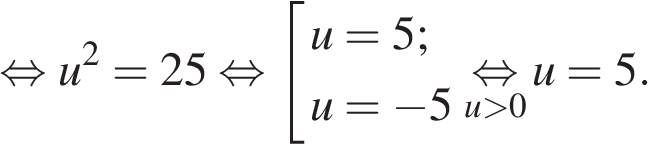
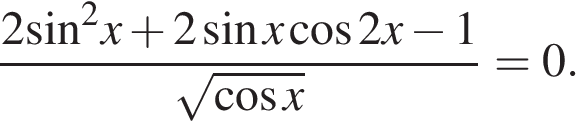
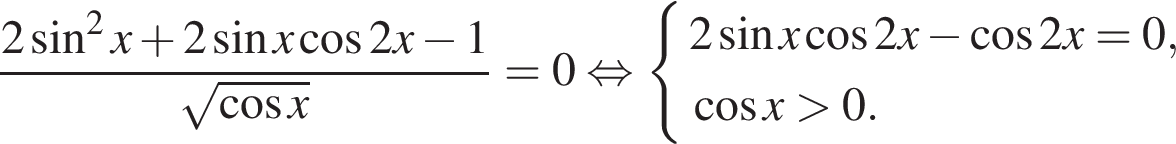
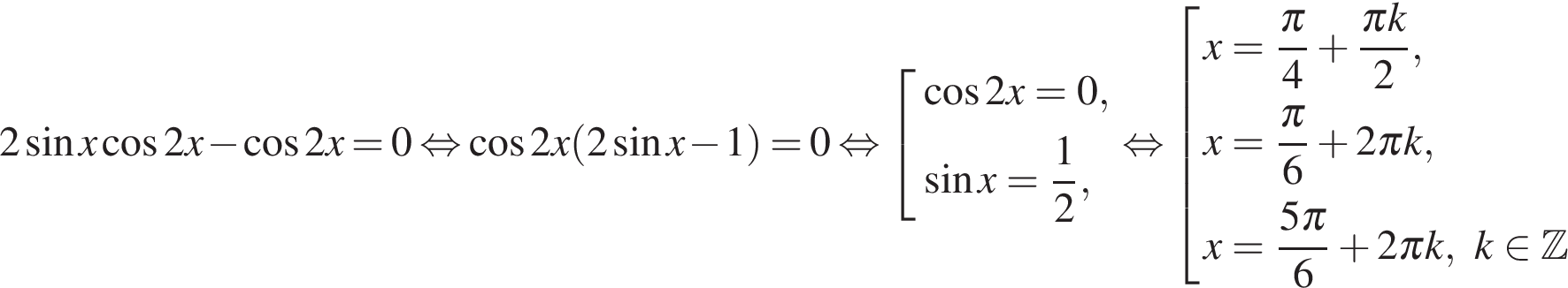
 Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см 
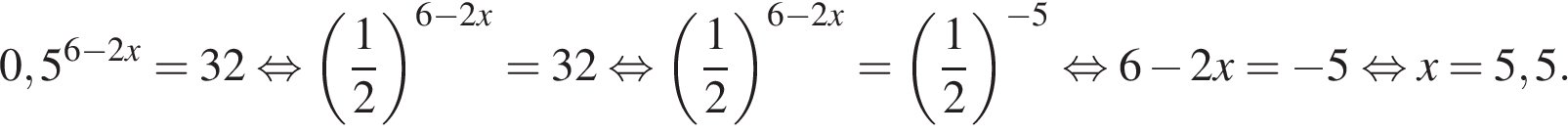
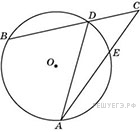 Угол ACB равен
Угол ACB равен 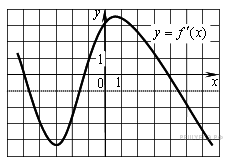 На рисунке изображен график производной функции
На рисунке изображен график производной функции 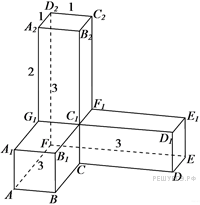 Найдите угол
Найдите угол 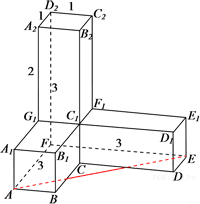
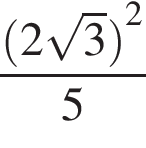 .
.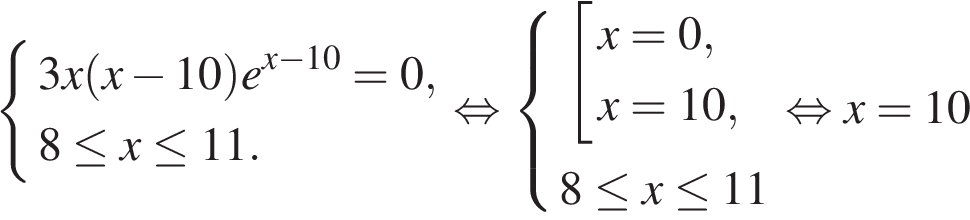
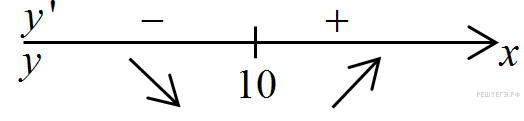
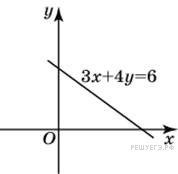 Найдите угловой коэффициент прямой, заданной уравнением 3x + 4y = 6.
Найдите угловой коэффициент прямой, заданной уравнением 3x + 4y = 6.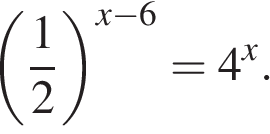
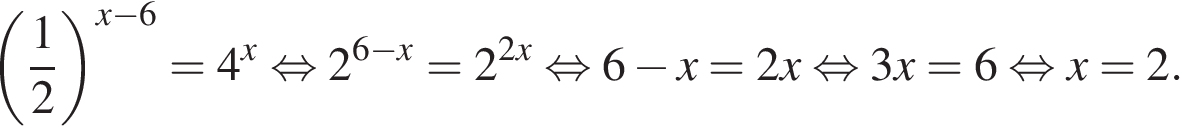
 В треугольнике ABC угол C равен
В треугольнике ABC угол C равен 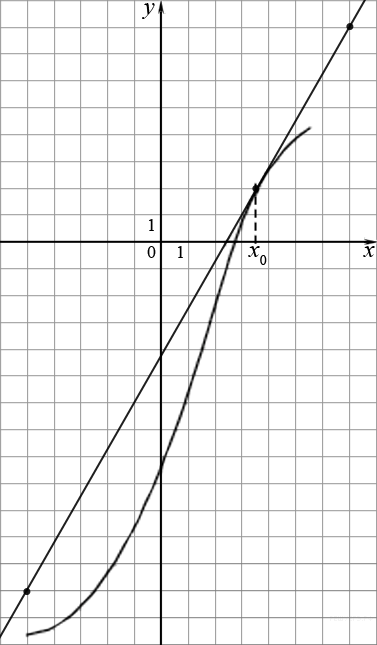
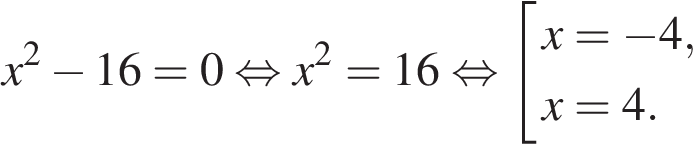
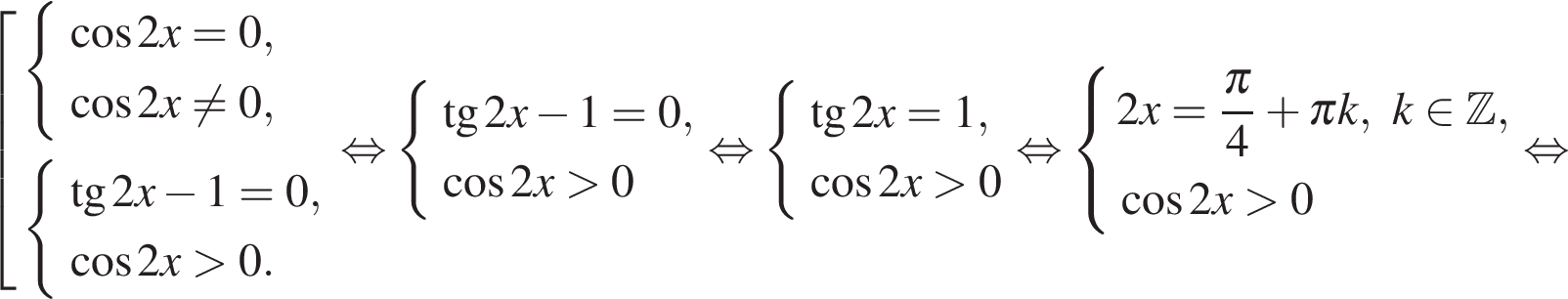
 Найдите площадь прямоугольной трапеции, изображенной на рисунке.
Найдите площадь прямоугольной трапеции, изображенной на рисунке. 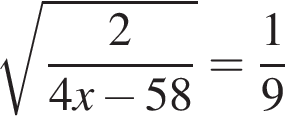 .
.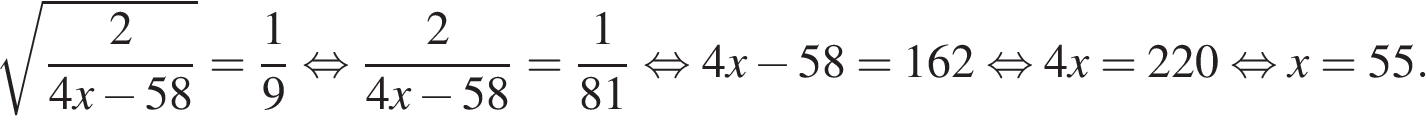
 Найдите площадь ромба, если его диагонали равны 4 и 12.
Найдите площадь ромба, если его диагонали равны 4 и 12.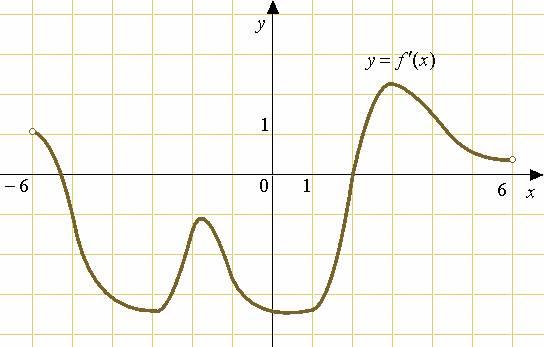
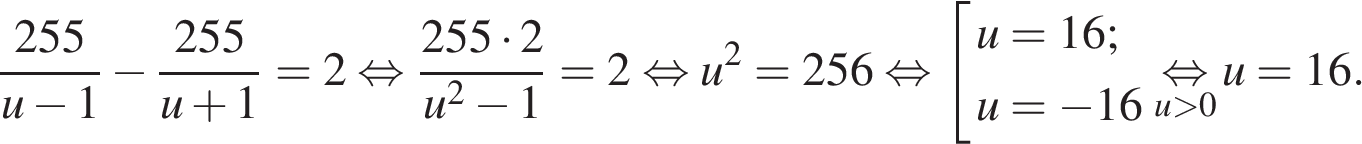
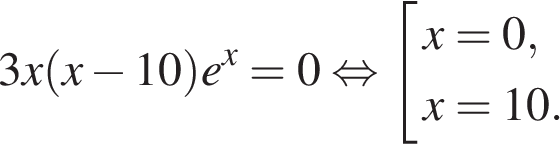
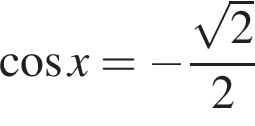 откуда
откуда