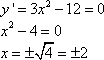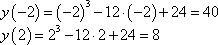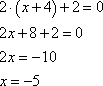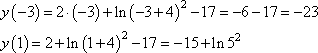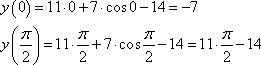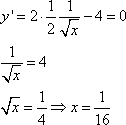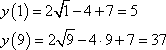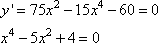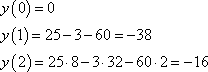Специально к окончанию учебного года! Скидки до 50% на комплекты видеоуроков и электронных тетрадей

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 23.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 13.05.2025 23:59

Яковлева Ирина Владимировна

Учитель математики

289 759

Подписчики

193

Подписки

Местоположение

Россия, Калининградская область

Специализация

Математика

Внеурочка

Классному руководителю

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

ЕГЭ профильный уровень. Задание №12. Наибольшее и наименьшее значения функции.

Категория: Математика

05.05.2019 15:10

ЕГЭ профильный уровен. Задание №12. Наибольшее и наименьшее значения функции. Представлены 10 заданий с решениями. Есть возможность пройти онлайн-тест по данным заданиям. (См. тест на моей странице). Использовались материалы сайта http://self-edu.ru

Просмотр содержимого документа
«ЕГЭ профильный уровень. Задание №12. Наибольшее и наименьшее значения функции.»

ЕГЭ ПРОФИЛЬНЫЙ УРОВЕНЬ

ЗАДАНИЕ №12 (НОВОЕ)

НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ.

Найдите точку максимума функции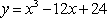

Решение. Чтобы найти точки экстремума функции, вычислим ее производную и приравняем результат нулю, получим:

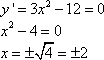
Найдем точку, в которой функция принимает наибольшее значение:

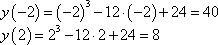
Имеем точку максимума x=-2.

Ответ: -2.

Найдите точку минимума функции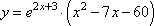

Решение. Можно заметить, что первый множитель 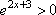при любых x и является монотонно возрастающей функцией. Поэтому точку минимума можно найти из рассмотрения альтернативной функции

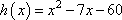которая представляет собой параболу с координатой вершины по оси Ox:

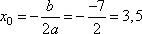
Это и есть точка минимума функции.

Ответ: -3,5.

Найдите наименьшее значение функции 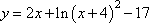на интервале [-3; 1].

Решение. Сначала найдем точки экстремума функции. Вычислим производную и приравняем результат нулю, получим:

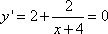
откуда

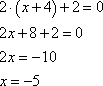
Данная точка не принадлежит диапазону [-3; 1]. Найдем значения функции на границах интервала:

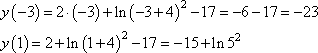
Отсюда видно, что наименьшее значение равно -23.

Ответ: -23.

Найдите наименьшее значение функции 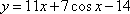на интервале .

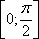Решение. Найдем точки экстремума функции. Приравняем производную нулю, получим:

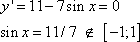
Точки экстремума отсутствуют. Вычислим значения функции на границах интервала:

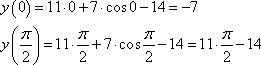
Видно, что наименьшее значение функции равно -7.

Ответ: -7.

Найдите наибольшее значение функции 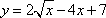на отрезке [1; 9].

Решение. Сначала найдем точки экстремума функции:

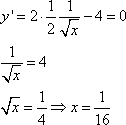
Данная точка не принадлежит промежутку [1; 9]. Вычислим значения функции на границах интервала, получим:

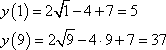
Наибольшее значение функции в промежутке [1; 9] равно 37.

Ответ: 37.

Найдите наименьшее значение функции на отрезке [0; 2].

Решение. Сначала найдем точки экстремума функции:

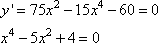
Пусть 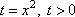, имеем:

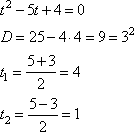
И обратная подстановка, дает:

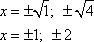
Диапазону [1;2] принадлежат только точки x=1; 2. Вычислим значения функции в точках экстремума и на границах диапазона, имеем:

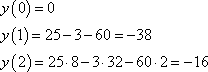
Имеем наименьшее значение функции -38.

Ответ: -38.

Найдите наибольшее значение функции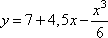

Решение. Вычислим точки экстремума функции, получим:

Вычислим значения функции в точках экстремума:

Наибольшее значение функции равно 16.

Ответ: 16.

Найдите наименьшее значение функции на отрезке .

Решение. Сначала найдем точки экстремума функции:

то есть, точек экстремума нет. Вычислим значения функции на границах диапазона:

Наименьшее значение равно 9.

Ответ: 9.

Найдите точку минимума функции

Решение. Здесь можно заметить, что множитель при любых x и соответствует монотонно возрастающей функции. Следовательно, точку минимума можно найти по альтернативной функции

которая представляет собой параболу с ветвями, направленными вверх. Координата ее вершины на оси Ox может быть вычислена как

Это и есть точка минимума функции.

Ответ: -3.