

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Ehtimolliklar haqida
Просмотр содержимого документа
«Ehtimolliklar haqida»
A.A.Abdushukurov
EHTIMOLLAR NAZARIYASI VA MATEMATIK STATISTIKA
Toshkent-2010


A.A.Abdushukurov
EHTIMOLLAR NAZARIYASI VA MATEMATIK STATISTIKA
Toshkent-2010

Taqrizchilar:
fizika-matematika fanlari doctori Ya.M. Xusanboyev fizika-matematika fanlari doctori Sh.Sh.Shorahmetov
Mundarija
Ki ri s h … ……… … ………………………………………… … . ……….. 8
EHTIMOLLAR NAZARIYASI
I bob. Tasodifiy hodisalar
1.1 Ehtimollar nazariyasinig predmeti……………………………..
9
1.2 Tasodifiy hodisalar, ularning klassifikatsiyasi………………….
11
1.3 Hodisalar ustida amallar………………………………………..
1.4 Tasodifiy hodisalar. Hodisalar algebrasi……………………….
11
14
1.5 Ehtimollikning statistik ta‘rifi…………………………………..
15
1.6 Ehtimollikning klassik ta‘rifi……………………………………
16
1.7 Ehtimollikning geometrik ta‘rifi………………………………..
20
1.8 Ehtimollikning aksiomatik ta‘rifi……………………………….
21
1.9 Ehtimollikning xossalari………………………………………..
22
1.10 Ehtimolliklar fazosi……………………………………………..
23
1.11 Shartli ehtimollik………………………………………………..
1.12 To‗la ehtimollik va Bayes formulalari…………………………
24
26
1.13 Bog‗liqsiz tajribalar ketma-ketligi. Bernulli formulasi…………
27
1.14 Limit teoremalar………………………………………………..
30
I bobga doir misollar………………………………………………….
35
II bob. Tasodifiy miqdorlar
2.1 Tasodifiy miqdor tushunchasi…………………………………..
39
2.2 Diskret tasodifiy miqdorning taqsimot qonuni………………….
2.3 Taqsimot funksiyasi va uning xossalari.………………………..
40
41
2.4 Zichlik funksiyasi va uning xossalari…………………………...
43
2.5 Tasodifiy miqdorning sonli xaraktiristikalari………………….
45
2.6 Ba‘zi muhim taqsimotlar………………………………………
49
II bobga doir misollar…………………………………………………
60
III bob. Ko‘p o‘lchovli tasodifiy miqdorlar
3.1 Ko‗p o‗lchovli tasodifiy miqdorlar va ularning birgalikdagi
65
taqsimot funksiyasi……………………………………………..
3.2 Ikki o‗lchovli diskret tasodifiy miqdor va uning taqsimot
66
qonuni …………………………………………………………..
3.3 Ikki o‗lchovli tasodifiy miqdorning taqsimot funksiyasi va
uning xossalari…………………………………………………..
67
3.4 Ikki o‗lchovli uzluksiz tasodifiy miqdor zichlik funksiyasi va
uning xossalari …………………………………………………
70
3.5 Tasodifiy miqdorlarning bog‗liqsizligi ………………………..
75
3.6 Shartli taqsimot qonunlari ………………………………………
76
3.7 Ikki o‗lchovli tasodifiy miqdorlarning sonli xarakteristikalari …
3.8 Ba‘zi muhim ikki o‗lchovli taqsimotlar ………………….…….
79
82
3.9 Xarakteristik funksiyalar va ularning xossalari…………………
89
III bobga doir misollar…………………………………………………
91
IV bob. Tasodifiy miqdorlarning funksiyalari
4.1 Bir argumentning funksiyalari…………………………………
4.2 Ikki argumentning funksiyalari…………………………………
95
IV bobga doir misollar………………………………………………..
99
103
V bob. Ehtimollar nazariyasining limit teoremalari
5.1 Chebishev tengsizligi…………………………………………..
5.2 Katta sonlar qonuni. Chebishev va Bernulli teoremalari ………
105
5.3 Markaziy limit teorema…………………………………………
107
109
V bobga doir misollar…………………………………………………
111
MATEMATIK STATISTIKA
VI bob. Tanlanma va uning xarakteristikalari
6.1 Matematik statistika predmeti…………………………………..
113
6.2 Bosh va tanlanma to‗plam………………………………………
114
6.3 Empirik taqsimot funksiya……………………………………...
115
6.4 Gistogramma va poligon ……………………………………….
118
6.5 Tanlanma xarakteristikalari…………………………………….
120
VI bobga doir misollar………………………………………………..
121
VII bob. Noma’lum parametrlarni baholash
7.1 Statistik baholar va ularning xossalari …………………………
124

7.2 Nuqtaviy baholash usullari……………………………………..
127
7.3 Interval baholash………………………………………………..
130
VII bobga doir misollar……………………………………………….
137
VIII bob. Statistik gipotezalarni tekshrish
8.1 Statistik gipotezalar. Statistik gipotezalarni tekshirish
alomatlari va ularning xossalari ………………………………..
139
8.2 Parametrik statistik alomat tuzish usullari………………………
142
8.3 Noparametrik muvofiqlik alomatlari……………………………
8.4 Matematik kutilma va dispersiyalar haqidagi statistik
145
gipotezalarni tekshirish………………………………………….
148
VIII bobga doir misollar………………………………………………
151
IX bob. Ko‘p o‘lchovli statistik tahlil usullari
9.1 Faktorli tahlil…………………………………………………..
9.2 Bosh komponentalar usuli……………………………………..
152
9.3 IX bobga doir misollar…………………………………………
154
158
Ilovalar……………………………………………………………….
Foydalanilgan adabiyotlar……………………………………………
159
163

Kirish
Ushbu o‗quv qo‗llanma muallifi ehtimollar nazariyasi va matematik statistika fanini ko‗pgina oliy ta‘lim muassasalarida taxsil olayotgan talabalarga tushunarli bo‗lishi uchun engil shaklda bayon qilishni o‗z oldiga maqsad qilib oldi. Tuzilishi bo‗yicha o‗quv qo‗llanma uning nomiga moniy ravishda ikki qismga bo‗linadi: ―ehtimollar nazariyasi‖ va
― matematik statistika‖. Qo‗lllanma materiallarini bayon qilishda har bir tushuncha va mavzularga oid tipik masala va misollar keltirishga e‘tibor berilib, har bir bobning so‗ngida talabalar mustaqil ishlashlari uchun bir qator misollar to‗plami keltirilgandir. Muallif murakkab matematik hisoblarni chetlab o‗tish bilan bir qatorda ko‗rilayotgan masalalarning nazariy – ehtimoliy va statistik mohiyatiga chuqurroq e‘tibor berib o‗tgandir.
Ushbu qo‗llanmani ehtimollar nazariyasi va matematik statistika fani o‗qitilishi nazarda tutilgan barcha bakalavriat ta‘lim yo‗nalishlari hamda magistratura mutahassisliklariga tavsiya etish mumkin. Undan ilmiy tadqiqot izlanishlarida ham foydalanish mumkin.
I bob. Tasodifiy hodisalar
1.1 Ehtimollar nazariyasining predmeti
Ehtimollar nazariyasi ―tasodifiy tajribalar‖, ya‘ni natijasini oldindan aytib bo‗lmaydigan tajribalardagi qonuniyatlatni o‗rganuvchi matematik fandir. Bunda shunday tajribalar qaraladiki, ularni o‗zgarmas (ya‘ni, bir xil) shartlar kompleksida hech bo‗lmaganda nazariy ravishda ixtiyoriy sonda takrorlash mumkin, deb hisoblanadi. Bunday tajribalar har birining natijasi tasodifiy hodisa ro‗y berishidan iboratdir. Insoniyat faoliyatining deyarli hamma sohalarida shunday holatlar mavjudki, u yoki bu tajribalarni bir xil sharoitda ko‗p matra takrorlash mumkin bo‗ladi. Ehtimollar nazariyasini sinovdan-sinovga o‗tishida natijalari turlicha bo‗lgan tajribalar qiziqtiradi. Biror tajribada ro‗y berish yoki bermasligini oldindan aytib bo‗lmaydigan hodisalar tasodifiy hodisalar deyiladi. Masalan, tanga tashlash tajribasida har bir tashlashga ikki tasodifiy hodisa mos keladi: tanganing gerb tomoni tushishi yoki tanganing raqam tomoni tushishi. Albatta, bu tajribani bir marta takrorlashda shu ikki tasodifiy hodisalardan faqat bittasigina ro‗y beradi. Tasodifiy hodisalarni biz tabiatda, jamiatda, ilmiy tajribalarda, sport va qimor o‗yinlarida kuzatishimiz mumkin. Umumlashtirib aytish mumkinki, tasodifiyat elementlarisiz rivojlanishni tasavvur qilish qiyindir. Tasodifiyatsiz umuman hayotning va biologik
yuzaga kelishini, insoniyat tarihini, insonlarning ijodiy
turlarning faoli ya tini, b o ‗ l m a y di.
etib
sotsial-iqtisodiy tizimlarning rivojlanishini tasavvur
E hti m oll a r n aza r i ya s i e s a ay n a n m a na s h u nd a y tas o d i f i y
bog‗liqliklarning matematik modelini tuzish bilan shug‗illanadi. Tasodifiyat insoniyatni doimo qiziqtirib kelgandir. Shu sababli ehtimollar nazariyasi boshqa matematik fanlar kabi amaliyot talablariga mos ravishda rivojlangan. Ehtimollar nazariyasi boshqa matematik fanlardan farqli o‗laroq nisbatan qisqa, ammo o‗ta shijoatlik rivojlanish tarixiga ega. Endi qisqacha tarixiy ma‘lumotlarni keltiramiz. Ommaviy tasodifiy hodisalarga mos masalalarni sistematik ravishda o‗rganish va ularga mos matematik apparatning yuzaga kelishi XVII asrga to‗g‗ri keladi. XVII asr boshida, mashhur fizik Galiley fizik o‗lchashlardagi xatoliklarni tasodifiy deb hisoblab, ularni ilmiy tadqiqot qilishga uringan. Shu davrlarda kasallanish, o‗lish, baxtsiz hodisalar statistikasi va shu kabi ommaviy tasodifiy hodisalardagi qonuniyatlarni tahlil qilishga asoslangan sug‗urtalanishning umumiy nazariyasini yaratishga ham urinishlar bo‗lgan. Ammo, ehtimollar nazariyasi matematik ilm sifatida murakkab tasodifiy jarayonlarning
o‗rganishdan emas, balki eng sodda qimor o‗yinlarini tahlil qilish natijasida yuzaga kela boshlagan. Shu boisdan ehtimollar nazariyasining paydo bo‗lishi XVII asr ikkinchi yarmiga mos keladi va u Paskal (1623- 1662), Ferma (1601-1665) va Gyuygens (1629-1695) kabi olimlarning qimor o‗yinlarini nazariyasidagi tadqiqotlari bilan bog‗liqdir. Ehtimollar nazariyasi rivojidagi katta qadam Yakov Bernulli (1654-1705) ilmiy izlanishlari bilan bog‗liqdir. Unga, ehtimollar nazariyasining eng muhim qonuniyati, deb hisoblanuvchi ―katta sonlar qonuni‖ tegishlidir. Ehtimollar nazariyasi rivojidagi yana bir muhim qadam de Muavr (1667-1754) nomi bilan bog‗liqdir. Bu olim tomonidan normal qonun (yoki normal taqsimot) deb ataluvchi muhim qonuniyat mavjudligi sodda holda asoslanib berildi. Keyinchalik, ma‘lum bo‗ldiki, bu qonuniyat ham, ehtimollar nazariyasida muhim rol‘ o‗ynar ekan. Bu qonuniyat mavjudligini asoslovchi teoremalar
― markaziy limit teoremalar‖ deb ataladi. Ehtimollar nazariyasi rivojlanishida katta hissa mashhur matematik Laplasga (1749-1827) ham tegishlidir. U birinchi bo‗lib ehtimollar nazariyasi asoslarini qat‘iy va
sistematik ravishda ta‘rifladi, markaziy limit teoremasining bir formasini isbotladi (Muavr-Laplas teoremasi) va ehtimollar nazariyasining bir necha
tadbiqlarini keltirdi. Ehtimollar nazariyasi rivojidagi etarlicha darajada
oldinga siljish Gauss (1777-1855) nomi bilan bog‗liqdir. U normal qonuniyatga yanada umumiy asos berdi va tajribadan olingan sonli ma‘lumotlarni qayta ishlashning muhim usuli – ―kichik kvadratlar usuli‖ni yaratdi. Puasson (1781-1840) katta sonlar qonunini umumlashtirdi va ehtimollar nazariyasini o‗q uzish masalalariga qo‗lladi. Uning nomi bilan ehtimollar nazariyasida katta rol‘ o‗ynovchi taqsimot qonuni nomlangandir. XVII va XIX asrlar uchun ehtimollar nazariyasining keskin rivojlanishi va u bilan har tomonlama qiziqish xarakterlidir. Keyinchalik ehtimollar nazariyasi rivojiga Rossiya olimlari V.Ya. Bunyakovskiy (1804- 1889), P.L. Chebishev (1821-1894), A.A. Markov (1856-1922), A.M.
Lyapunov (1857-1918), A.Ya. Xinchin (1894-1959), V.I. Romanovskiy ( 1 8 7 9 - 1 9 5 4), A . N. Kol m ogorov ( 1 9 0 3 - 1 9 8 7 ) va ula r n i n g s h o g i r d la r i
bebaho hissa qo‗shdilar. O‗zbekistonda butun dunyoga taniqli Sarimsokov (1915-1995) va S.X. Sirojiddinov (1920-1988) larning muhim rollarini
alohida ta‘kidlab o‗tish joizdir.
1.2 Tasodifiy hodisalar, ularning klassifikatsiyasi
Dastlab ehtimollar nazariyasining asosiy tushunchalaridan biri
― tasodifiy hodisa‖ tushunchasini keltiramiz. Natijasini oldindan aytib bo‗lmaydigan tajriba o‗tkazilayotgan bo‗lsin. Bunday tajribalar ehtimollar nazariyasida tasodifiy deb ataladi.
- Tasodifiy hodisa (yoki hodisa) deb, tasodifiy tajriba natijasida ro‗y
berishi oldindan aniq bo‗lmagan hodisaga aytiladi.
Hodisalar, odatda, lotin alifbosining bosh harflari A, B, C, …lar bilan belgilanadi.
- Tajribaning har qanday natijasi elementar hodisa deyiladi va
orqali belgilanadi.
- Tajribaning natijasida ro‗y berishi mumkin bo‗lgan barcha elementar hodisalar to‗plami elementar hodisalar fazosi deyiladi va orqali belgilanadi.
1.1-misol. Tajriba nomerlangan kub(o‗yin soqqasi)ni tashlashdan iborat bo‗lsin. U holda tajriba 6 elementar hodisadan hodisalar 1 , 2 , 3 , 4 , 5 , 6
lardan iborat bo‗ladi. i hodisa tajriba natijasida i ( i 1,2,3,4,5,6) ochko tushishini bildiradi. Bunda elementar hodisalar fazosi: {1,2,3,4,5,6} .
- Tajriba natijasida albatta ro‗y beradigan hodisaga muqarrar hodisa
deyiladi.
Elementar hodisalar fazosi muqarrar hodisaga misol bo‗la oladi.
Aksincha, umuman ro‗y bermaydigan hodisaga mumkin bo‗lmagan hodisa deyiladi va u orqali belgilanadi.
1.1-misolda keltirilgan tajriba uchun quyidagi hodisalarni kiritamiz:
A ={5 raqam tushishi}; B ={juft raqam tushishi}; C ={7 raqam tushishi}; D ={butun raqam tushishi};
Bu yerda A va B hodisalar tasodifiy, C hodisa mumkin bo‗lmagan va D
hodisa muqarrar hodisalar bo‗ladi.
1.3 Hodisalar ustida amallar
Tasodifiy hodisalar orasidagi munosabatlarni keltiramiz:
- A va B hodisalar yig‘indisi deb, A va B hodisalarning kamida
B birgalikda) ro‗y berishidan
bittas i (y a ‘ n i yo ki A , y oki B , y oki A va
iborat С A B ( C A B ) hodisaga aytiladi.
B h o d isa l a r k o ‘ p a y tmas i d e b, A va
B h o d i s a lar i k k il a s i b e r i s h ida n i b orat
A va h a m ( y a ‘ n i
va birgalikda)ro‗y
B
A
C A B ( C A B ) h od i s a ga ay tiladi.
A hodisadan B hodisaning ayirmasi deb, A hodisa ro‗y berib, B hodisa ro‗y bermasligidan iborat C A \ B ( C A - B ) hodisaga aytiladi.
- A hodisaga qarama-qarshi A hodisa faqat va faqat A hodisa ro‗y
bermaganda ro‗y beradi(ya‘ni A hodisa A hodisa ro‗y bermaganda ro‗y beradi). A ni A uchun teskari hodisa deb ham ataladi.
- Agar A hodisa ro‗y berishidan B hodisaning ham ro‗y berishi kelib
chiqsa A hodisa B hodisani ergashtiradi deyiladi va A B ko‗rinishida yoziladi.
- Agar A B va B A b o ‗ l s a , u hol d a A va B hod i s ala r ten g ( teng kuchli ) hodisalar deyiladi va A B ko‗rinishida yoziladi.
1.2-misol. A , B va C -ixtiyoriy hodisalar bo‗lsin. Bu hodisalar orqali
quyidagi hodisalarni ifodalang: D ={uchchala hodisa ro‗y berdi}; E ={bu hodisalarning kamida bittasi ro‗y berdi}; F ={bu hodisalarning birortasi ham ro‗y bermadi}; G ={bu hodisalarning faqat bittasi ro‗y berdi}.
Hodisalar ustidagi amallardan foydalanamiz: D A B C ( D A B C ) ;
E A B C ; F A B C ; G A B C A B C A B C .
Demak hodisalarni to‗plamlar kabi ham talqin etish mumkin ekan.
Belgilash
To‗plamlar nazariyasidagi talqini
Ehtimollar nazariyasidagi talqini
Fazo (asosiy to‗plam)
,
A , A
Elementar hodisalar fazosi,
fazo elementlari
A B , A B
A to‗plam
elementar hodisa
muqarrar hodisa
A B , A B
A hodisa
A va B to‗plamlarning yig‗indisi, birlashmasi
A \ B , A B
A va B hodi s a lar y i g ‗ indisi ( A va B ning kamida biri ro‗y berishidan iborat hodisa)
A va B to‗plamlarning kesishmasi
A va B hodisalar ko‗paytmasi
A t o ‗ pla m d a n
A
A ho d i s a d a n B ho d i s a n i ng ay i r m a si( A ning r o ‗y beri s h i,
( A va B ni n g bi r g a li k da r o ‗y berishidan iborat hodisa)
Bo‗sh to‗plam
B t o ‗ pla m ni n g ay i r m asi
Mumkin bo‗lmagan hodisa
A to‗plamga to‗ldiruvchi
B ning r o ‗y ber m a sligi d a n i b orat hodisa)
A ho d i s a ga t e sk a ri ho di s a ( A
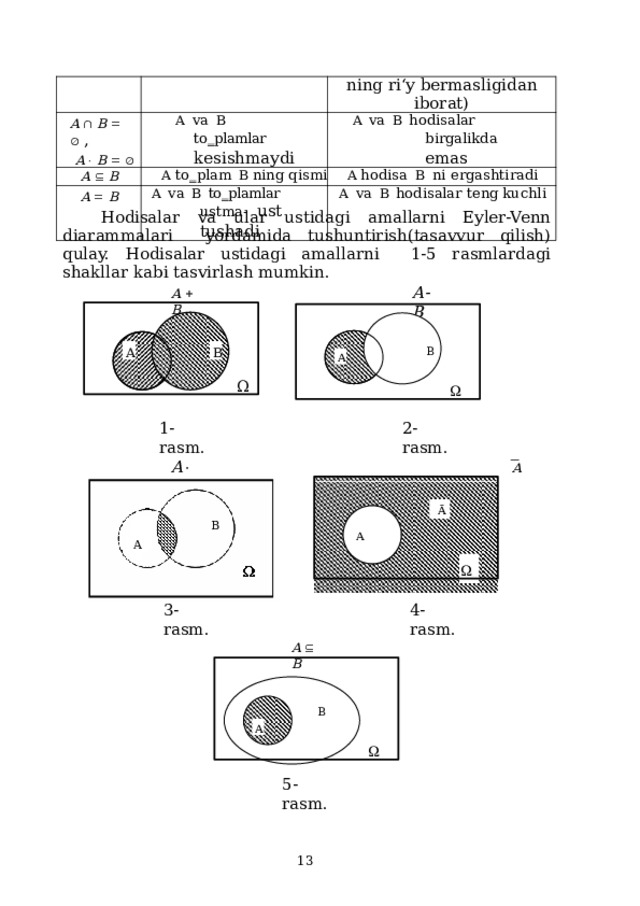
A B ,
ning ri‘y bermasligidan iborat)
A B
A va B to‗plamlar kesishmaydi
A B
A va B hodisalar birgalikda emas
A t o ‗ plam B ning q i s m i
A B
A ho d i s a B ni e r g a s h tir a di
A va B to‗plamlar ustma- ust tushadi
A va B hodisalar teng kuchli
Hodisalar va ular ustidagi amallarni Eyler-Venn diarammalari yordamida tushuntirish(tasavvur qilish) qulay. Hodisalar ustidagi amallarni 1-5 rasmlardagi shakllar kabi tasvirlash mumkin.
A -B
A B
Ω
B
B
A
A
1-rasm.
2 -ras m .
A B
A
Ā
A
B
A
3 -rasm.
4-rasm.
A B
B
A
5-rasm.
Hodisalar ustidagi amallar quyidagi xossalarga ega:
A B B A ;
- A B B A ,
- ( A B ) C A C B C , ;
- ( A B ) C A ( B C ) , ( A B ) C A ( B C ) ;
- A A A ,
- A ,
- A A ,
- A B A B ;
- A B A B va A B A B - de Morgan ikkilamchilik prinsipi.
A A A ;
A A A A ,
A A ;
A ;
, A A ;
,
1.3-misol.
a) ( A B ) ( A B ) ifodani soddalashtiring. Yuqoridagi xossalardan foydalanamiz:
( A B ) ( A B ) A A A B B A B B A A ( B B ) A A A A A
De m a k, ( A B ) ( A B ) A e k a n.
b) A B A A B f o r m ulani is b ot la ng.
A B ( A B ) A B A B ( A A ) A ( A A ) B
A A B A B ( B ) A A B A A B A A B .
1.4 Tasodifiy hodisalar. Hodisalar algebrasi
Ehtimollar nazariyasining asosiy tushunchalarini keltiramiz.
Natijasi tasodifiy bo`lgan biror tajriba o`tkazilayotgan bo`lsin. -tajriba natijasida ro`y berishi mumkin bo`lgan barcha elementar hodisalar to`plami elementar hodisalar fazosi deyiladi; tajribaning natijasi esa elementar hodisa deyiladi.
- Agar chekli yoki sanoqli to`plam bo`lsa (ya`ni elementlarini natural sonlar yordamida nomerlash mumkin bo`lsa), u holda uning ixtiyoriy qism to`plami A tasodifiy hodisa (yoki hodisa) deyiladi: A .
to`plamdagi A qism to`plamga tegishli elementar hodisalar A
hodisaga qulaylik yaratuvchi hodisalar deyiladi.
- to`plam muqarrar hodisa deyiladi. - bo`sh to`plam mumkin bo`lmagan hodisa deyiladi.
S - ning qism to`plamlaridan tashkil topgan sistema bo`lsin.
- Agar
1 . S , S ;
- A S m uno s a b a t d a n A S k e l i b c hi q s a ;
- A S va B S munosabatdan A B S , A B S kelib chiqsa S sistema algebra tashkil etadi deyiladi.
Ta‘kidlash joizki, A B A B , A B A B ekanligidan 3 shartdagi A B S
va A B S munosabatlardan ixtiyoriy bittasini talab qilish yetarlidir.
1.4- m i sol. S , si ste m a a l g e bra tas h k i l e tadi: ,
, , .
Agar 3 s h a rt o ` rni g a qu y i d a g i lar n i ta lab qi l s a k A n S , n 1 , 2 , . .. ,
munosabatdan ∪ A n S , ∩ A n S kelib chiqsa S sistema -algebra deyiladi.
n 1
n 1
Agar c h e kli y oki
s a n o qli b o ‗ l s a , -t o ` p la m ni n g b a rcha q i sm
to`plamlaridan tashkil topgan hodisalar sistemasi algebra tashkil etadi.
1.5 Ehtimollikning statistik ta’rifi
A hodisa n ta bog‗liqsiz tajribalarda n A marta ro‗y bersin. n A son A
n A
hodisaning chastotasi, deyiladi.
munosabat esa A hodisaning nisbiy chastotasi
n
Nisbiy chastotaning statistik turg‗unlik xossasi deb ataluvchi xossasi mavjud, ya‘ni tajribalar soni oshishi bilan nisbiy chastotasi ma‘lum qonuniyatga ega bo‗ladi va biror son atrofida tebranib turadi.
Misol sifatida tanga tashlash tajribasini olaylik. Tanga A ={Gerb} tomoni bilan tushishi hodisasini qaraylik. Byuffon va K.Pirsonlar
tomonidan o‗tkazilgan tajribalar natijasi quyidagi jadvalda keltirilgan:
Tajriba
o‗tkazuvchi
Tajribalar soni, n
Byuffon
Tushgan gerblar
K.Pirson
4040
K.Pirson
12000
2048
soni, n A
Nisbiy chastota,
6019
24000
0.5080
n A /n
12012
0.5016
0.5005
Jadvaldan ko‗rinadiki, n ortgani sari n A /n nisbiy chastota 1 0.5 ga
2
yaqinlashar ekan.

- Agar tajribalar soni etarlicha ko‗p bo‗lsa va shu tajribalarda biror A hodisaning nisbiy chastotasi biror o‗zgarmas son atrofida tebransa, bu songa A hodisaning statistik ehtimolligi deyiladi.
A hodisaning ehtimolligi P(A) simvol bilan belgilanadi. Demak,
li m n A P ( A ) y oki ye tarl i c ha katta n lar uch u n n A P ( A ) .
n n
n
S tatis t ik e h t i m o l li k ning k a m c hili g i s hu n d a n i bora t ki, bu ye r d a
statistik ehtimollik yagona emas. Masalan, tanga tashlash tajribasida ehtimollik sifatida nafaqat 0.5, balki 0.49 yoki 0.51 ni ham olishimiz mumkin. Ehtimollikni aniq hisoblash uchun katta sondagi tajribalar o‗tkazishni talab qiladi, bu esa amaliyotda ko‗p vaqt va xarajatlarni talab qiladi.
Statistik ehtimollik quyidagi xossalarga ega:
1 . 0 P ( A ) 1 ;
2 . P ( ) 0 ;
3 . P ( ) 1 ;
4. A B bo‗lsa, u holda P ( A B ) P ( A ) P ( B ) ;
n 0 n A 1 .
Isboti. 1) Ihtiyoriy A hodisaning chastotasi uchun 0 n
A
n
n
0 P ( A ) 1 b o ‗ ladi.
E tarl i c ha katta n lar uch u n P ( A ) b o ‗ l g a ni u ch un
n A
- Mumkin bo‗lmagan hodisa uchun n A =0.
- Muqarrar hodisaning chastotasi n A = n.
- Agar A B b o ‗ l s a , u h ol d a n A B n A n B va
P ( A B ) n A B n A n B n A n B P ( A ) P ( B ) .
n n n n
■
1.6 Ehtimollikning klassik ta’rifi
chekli n ta teng imkoniyatli elementar hodisalardan tashkil topgan bo‗lsin.
- A h o d i s a n i ng e hti m o l l i g i d e b, A hod i s a ga qula y lik ya rat u v c hi elementar hodisalar soni k ning tajribadagi barcha elementar hodisalar soni
n ga nisbatiga aytiladi.
( 1 .6.1)
P ( A ) N ( A ) k
N ( ) n

Klassik ta‘rifdan foydalanib, ehtimollik hisoblashda kombinatorika elementlaridan foydalaniladi. Shuning uchun kombinatorikaning ba‘zi elementlari keltiramiz. Kombinatirikada qo‗shish va ko‗paytirish qoidasi deb ataluvchi ikki muhim qoida mavjud.
A { a 1 , a 2 ,..., a n } va B { b 1 , b 2 ,..., b m } chekli to‗plamlar berilgan bo‗lsin.
- Qo‘shish qoidasi: agar A to‗plam elementlari soni n va B to‗plam elementlari soni m bo‗lib, A B ( A va B to‗plamlar kesishmaydigan) bo‗lsa, u holda A B to‗plam elementlari soni n+m bo‗ladi.
- Ko‘paytirish qoidasi: A va B to‗plamlardan tuzilgan barcha ( a i , b j )
juftliklar to‗plami C {( a i , b j ) : i 1, n , j 1, m } ning elementlari soni n m
bo‗ladi.
n ta elementdan m ( 0 m n )tadan tanlashda ikkita sxema mavjud: qaytarilmaydigan va qaytariladigan tanlashlar. Birinchi sxemada olingan elementlar qayta olinmaydi(orqaga qaytarilmaydi), ikkinchi sxemada esa har bir olingan element har qadamda o‗rniga qaytariladi.
I. Qaytarilmaydigan tanlashlar sxemasi
- Guruhlashlar soni: n ta elementdan m ( 0 m n )tadan guruhlashlar soni quyidagi formula orqali hisoblanadi:
n !
( 1 .6.2)
C m
n
m ! ( n m )!
С sonlar Nyuton binomi formulasining koeffisientlaridir:
m
n
n
2 n 2 2
n n 1 n 1
.
( p q ) p C p q C p q .. . q
n
n
- O ‘ r i n l a s h t i rish l a r s o n i: n ta e le m ent d an m ( 0 m n ) tadan o‗rinlashtirishlar soni quyidagi formula orqali hisoblanadi:
n !
. ( 1 .6.3)
A m
n
( n m )!
- O‘rin almashtirishlar soni: n ta elementdan n tadan o‗rinlashtirish o‗rin almashtirish deyiladi va u quyidagicha hisoblanadi:
P n n ! .
( 1 .6.4)
O‗rin almashtirish o‗rinlashtirishning
x u s u s iy h o li d i r , c hunki a g a r
n !
(1.6.3.)da n=m bo‗lsa
n ! n ! bo‗ladi.
m
A
n
( n m ) ! 0 !
II. Qaytariladigan tanlashlar sxemasi
- Qaytariladigan guruhlashlar soni: n ta elementdan m ( 0 m n ) tadan qaytariladigan guruhlashlar soni quyidagi formula orqali hisoblanadi:
m
m
( 1 .6.5)
C С
n
n m 1
- Qaytariladigan o‘rinlashtirishlar soni: n ta elementdan m ( 0 m n ) tadan q ay tari l a d i g a n o ‗ r i nlas h tir is h lari s oni q u y i d a gi f o r m ula orqali hisoblanadi:
m
. ( 1 .6.6)
m
A n
n
- Qaytariladigan o‘rin almashtirishlar soni: k hil n ta elementdan iborat to‗plamda 1-element n 1 marta, 2-element n 2 marta,…, k- element n k
marta qaytarilsin va bo‗lsin, u holda n ta elementdan
n 1 n 2 .. . n k n
iborat o‗rin almashtirish P n ( n 1 , n 2 ,..., n k ) orqali belgilanadi va u quyidagicha hisoblanadi:
n !
P n ( n 1 , n 2 ,... , n k )
. ( 1 .6.4)
n ! n !... n !
1 2 k
Endi ehtimollik hisoblashga doir misollar keltiramiz.
1.5-misol. Telefon nomerini terayotganda abonent oxirgi ikki raqamni eslay olmadi. U bu raqamlar har xil ekanligini eslab, ularni tavakkaliga terdi. Telefon nomeri to‗g‗ri terilganligi ehtimolligini toping.
Oxirgi ikki raqamni A usul bilan terish mumkin. A ={telefon nomeri
2
10
to‗g‗ri terilgan} hodisasini kiritamiz. A hodisa faqat bitta elementdan iborat bo‗ladi(chunki kerakli telefon nomeri bitta bo‗ladi). Shuning uchun klassik
1 1
1 0.011 .
ta‘ri f ga k o ‗ ra P ( A ) N ( A )
A 2
N ( )
1 0 9 90
10
1.6-misol. 100 ta lotoreya biletlarlaridan bittasi yutuqli bo‗lsin.
T a v a kk a liga o l in ga n
10 lotoreya biletlari ichida yutuqlisi bo‗lishi
ehtimolligini toping.
C 10
100 ta lotoreya biletlaridan 10 tasini
usul bilan tanlash mumkin.
10 0
B ={10 lotoreya biletlari ichida yutuqlisi bo‗lishi } hodisasi bo‗lsa,
N ( B ) C 1 C 9 1
1 99
va P ( B )
0 . 1 .
N ( B ) C 1 C 9
C 10
1 99
N ( )
10
1 0 0
1.7-misol. Pochta bo‗limida 6 xildagi otkritka bor. Sotilgan 4 ta otkritkadan: a) 4 tasi bir xilda; b) 4 tasi turli xilda bo‗lishi ehtimolliklarini toping.
6 xil otkritkadan 4 tasini C usul bilan tanlash mumkin. a) A ={4 ta
4
6
bir xildagi otkritka sotilgan} hodisasi bo‗lsin. A hodisaning elementar hodisalari soni otkritkalar xillari soniga teng, ya‘ni N(A) =6. Klassik
6 6 1
P ( A ) N ( A )
ta‘rifga ko‗ra
bo‗ladi. b) B={4 ta har xil
C 4
N ( )
1 2 6 21
6
otkri t ka s o ti l g a n} h o d i s a s i b o ‗ l s i n, u h o l d a
ga t e ng va
N( B ) C 4
6
C 4
1 5 5
N ( B )
6
.
P ( B )
C 4
1 26 42
N ( )
6
Klassik ehtimollik quyidagi xossalarga ega: 1. P ( ) 0 ;
2 . P ( ) 1 ;
3 . 0 P ( A ) 1 ;
- Agar A B b o ‗ l s a , u h o ld a P ( A B ) P ( A ) P ( B ) ;
- A , B u c hun P ( A B ) P ( A ) P ( B ) P ( A B )
Isboti. 1) N ( ) 0 bo‗lgani uchun klassik ta‘rifga ko‗ra P ( ) N ( ) 0 .
N ( )
2) Kla ss i k t a ‘ r i f ga k o‗ ra P ( ) N ( ) 1 .
N ( )
3) Ihtiyoriy A hodisa uchun A ekanligidan 0 P ( A ) 1 bo‗ladi.
4) A g a r A B b o ‗ l s a , u ho l da va
N ( A B ) N ( A ) N ( B )
P ( A B ) N ( A B ) N ( A ) N ( B ) N ( A ) N ( B ) P ( A ) P ( B ) .
N ( ) N ( ) N ( ) N ( )
5 ) A B va shaklida
B hodisalarni birgalikda bo‗lmagan ikki hodisalar yig‗ndisi
yozib olamiz:
B B B ( A A ) A B B A , u h ol d a 4 -
A B A B A ( 1.3 m i s o l ),
xo s s a ga k o ‗ ra va P ( B ) P ( A B ) P ( B A ) . B u i k k i
P ( A B ) P ( A ) P ( B A )
ten g l i kd a n P ( A B ) P ( A ) P ( B ) P ( A B ) k e lib c hi q a di. ■

1.7 Ehtimollikning geometrik ta’rifi
Ehtimolning klassik ta‘rifiga ko‗ra - elementar hodisalar fazosi
chekli bo‗lgandagina hisoblashimiz mumkin. Agar
i m koniy a tli e l e m entar h o d i s a lar d a n tas h k i l t o p g a n b o ‗ l s a , g e o m e t r ik
c h e k s iz teng
ehtimollikdan foydalanamiz.
O ‗ lch o v li bi r or G s oha b e r i l g a n bo‗lib, u D sohani o‗z ichiga olsin. G sohaga tavakkaliga tashlangan X nuqtani D sohaga tushishi ehtimolligini hisoblash masalasini ko‗ramiz. Bu yerda X nuqtaning G sohaga tushishi muqarrar va D sohaga tushishi tasodifiy hodisa
6 -ras m .
bo‗ladi. A { X D } -X nuqtaning D sohaga
tushishi hodisasi bo‗lsin.
- A hodisaning geometrik ehtimolligi deb, D soha o‗lchovini G soha o‗lchoviga nisbatiga aytiladi, ya‘ni
P ( A ) m e s { D } ,
mes { G }
bu yerda mes orqali uzunlik, yuza, hajm belgilangan.
1.8-misol. l uzunlikdagi sterjen tavakkaliga tanlangan ikki nuqtada bo‗laklarga bo‗lindi. Hosil bo‗lgan bo‗laklardan uchburchak yasash mumkin bo‗lishi ehtimolligini toping.
Birinchi bo‗lak uzunligini x , ikkinchi bo‗lak uzunligini y bilan belgilasak, uchinchi bo‗lak uzunligi l-x-y
b o ‗ ladi. B u ye r d a {( x , y ) : 0 x y l } ,
ya‘ni 0 x y l sterjenning bo‗laklari uzunliklarining barcha bo‗lishi mumkin
bo‗lgan b o ‗ lakl a r d a n
kombinatsiyasidir. uchburchak
B u ya s a s h
mumkin bo‗lishi uchun quyidagi shartlar
b a jari l ishi k e rak:
x y l x y ,
x l x y y , y l x y x .
7 -ras m .

Bulardan x l , ekanligi kelib chiqadi.
y l , x y l
2 2 2
Bu tengsizliklar 7-rasmdagi bo‗yalgan sohani bildiradi. Ehtimollikning geometrik ta‘rifiga ko‗ra:
1 l l
P ( A ) mes { A } 2 2 1 .
2
m e s { G } 4
1 l l
2
1.9-misol. (Uchrashuv haqida)
Ikki do‗st soat 9 bilan 10 orasida uchrashishga kelishishdi. Birinchi kelgan kishi do‗stini 15 daqiqa davomida kutishini, agar shu vaqt mobaynida do‗sti kelmasa u ketishi mumkinligini shartlashib olishdi. Agar ular soat 9 bilan 10 orasida ixtiyoriy momentda kelishlari mumkin bo‗lsa, bu ikki do‗stning uchrashishi ehtimolini toping.
B i r i n c hi k i s h i k e l g a n m om e nt n i x ,
ikkinchisinikini y bo‗lsin:
0 x 60 , 0 y 60 U holda ularning
u c h rashis h lari u c hun
x y 15
tengsizlik bajarilishi kerak.
De m a k, { ( x , y ) : 0 x 6 0 , 0 y 6 0 } ,
A { ( x , y ) : x y 1 5 } . x va y lar n i D e k a r t
tekisligida
koordinatalar tasvirlaymiz(8-rasm). U holda
6 0 2 2 1 4 5 45
2
P ( A ) m e s { A }
7 .
mes { G }
16
60 2
8-rasm.
1.8 Ehtimollikning aksiomatik ta’rifi
E hti m oll a r n aza r i y a s i n i a k s i o m a tik qu r i s h d a A . N. Kol m ogorov tomonidan 30-yillarning boshlarida asos solingan.
- biror tajribaning barcha elementar hodisalar to‗plami, S -hodisalar algebrasi bo‗lsin.

- S hodisalar algebrasida aniqlangan, haqiqiy qiymatlar qabul qiluvchi P ( A ) fuksiya ehtimollik deyiladi, agar u uchun quyidagi aksiomalar o‗rinli bo‗lsa:
A1: ihtiyoriy hodisaning ehtimolligi manfiy emas
A S P ( A ) 0
(nomanfiylik aksiomasi);
A2: m uq a r r a r ho d i s a n i ng eh ti m o l l i g i bi r ga te n g
P ( ) 1
(normallashtirish aksiomasi);
A3: juft-jufti bilan birgalikda bo‗lmagan hodisalar yig‗indisining ehtimolligi shu hodisalar ehtimollari yig‗indisiga teng, ya‘ni agar A i A j , i j bo‗lsa, u holda
P ( ∪ A k ) P ( A k )
k k
(additivlik aksiomasi);
( , S , P )
hodisalar fazosi,
u c hlik e hti m oll i k fa z o s i d ey il a di, bu ye r d a - e l e m e ntar
S -hodisalar algebrasi, P - A1-A3 aksiomalarni
qanoatlantiruvchi sanoqli funksiya.
1.9 Ehtimollikning xossalari
Kolmogorov aksiomalarining tatbiqi sifatida quyidagi xossalarni keltiramiz:
- Mumkin bo‗lmagan hodisaning ehtimoli nolga teng
P ( ) 0 .
- Qarama-qarshi hodisalarning ehtimolliklari yig‗indisi birga teng
P ( A ) P ( A ) 1 .
- Ixtiyoriy hodisaning ehtimolligi uchun quyidagi munosabat o‗rinli:
0 P ( A ) 1
- Agar A B b o‗ l sa , u h o ld a P ( A ) P ( B ) .
- Agar birgalikda bo‗lmagan A 1 , A 2 ,..., A n hodisalar to‗la gruppani
tashkil etsa, ya‘ni ∪ A i va A i A j , i j bo‗lsa u holda
i 1
n
n
P ( A i ) 1 .
i 1
Isboti:
- A A , A tengliklardan A3 aksiomaga ko‗ra
P ( A ) P ( ) P ( A ) P ( ) 0
- A A A A tengliklardan P ( A ) P ( A ) P ( ) hamda A2 va A3 aksiomalardan esa P ( A ) P ( A ) 1 tenglik kelib chiqadi.
- 2-xossaga ko‗ra P ( A ) 1 P ( A ) va A1 aksiomaga asosan 0 P ( A ) 1 .
- A B e k a nlig i d a n B ( B A ) A va ( B A ) A . A3 a k s i o m a ga k o ‗ r a
P ( B ) P ( B A ) P ( A ) , ammo P ( B A ) 0 bo‗lgani uchun P ( A ) P ( B ) .
- A 1 A 2 ... A n tenglik, A2 va A3 aksiomalarga ko‗ra
P ( A 1 A 2 ... A n ) P ( A 1 ) P ( A 2 ) ... P ( A n ) . ■
1.10 Ehtimolliklar fazosi
Elementar hodisalar fazosi cheksiz bo‗lsin: { 1 , 2 ,..., n ,...} . S esa
ning barcha qism to‗plamlaridan tashkil topgan hodisalar algebrasi bo‗lsin. Har bir i , i 1,2,... elementar hodisaga p ( i ) sonni mos qo‗yamiz. p ( i ) -elementar hodisaning ehtimoli deyiladi. Demak, da
quyidagi shartlarni qanoatlantiruvchi sonli p ( i ) funksiya kiritamiz:
1. i , P ( i ) 0 ;
2. p ( i ) 1 .
i 1
U holda A hodisaning ehtimolligi yig‗indi shaklida ifodalanadi:
P ( A ) P ( i )
i A
( 1 .1 0 .1)
Ehtimollikni bunday aniqlash Kolmogorov aksiomalarini qanoatlantiradi:
1. P ( A ) P ( i ) 0 , c hunki h a r bir P ( i ) 0 ;
i A
2. P ( ) p ( i ) p ( i ) 1 ;
n
i i 1
3. Agar A B b o‗ l sa , u h o l d a
P ( A B ) p ( i ) p ( i ) p ( i ) P ( A ) P ( B ) .
i A B i A i B

Bunday aniqlangan { , S , P } uchlik ehtimolliklar fazosi(yoki diskret ehtimolliklar fazosi) deyiladi.
Agar { 1 , 2 ,..., n } - chekli fazo va tajribadagi barcha elementar
hodisalar teng imkoniyatli bo‗lsa, ya‘ni
p ( ) p ( ) .. . p ( ) 1 ,
( 1 .1 0 . 2 )
1 2 n
n
u holda (1.10.1) formula quyidagi ko‗rinishga ega bo‗ladi:
P ( A ) p ( ) 1 1 .. . 1 m
(1.10.3)
n .
i
n – – n – – n
m
A
i
Bu yerda m A hodisaga tegishli elementar hodisalar soni. Bu esa ehtimollikni klassik ta‘rifga ko‗ra hisoblashdir. Demak, klassik ehtimol (1.10.1) formula orqali aniqlangan ehtimollikning xususiy holi ekan.
1.11 Shartli ehtimollik
A va B hodisalar biror tajribadagi hodisalar bo‗lsin.
- B hodisaning A hodisa ro‗y bergandagi shartli ehtimolligi deb,
P ( A B )
( 1 .1 1 .1)
( P ( A ) 0)
P ( A )
nisbatga aytiladi. Bu ehtimollikni P ( B / A ) orqali belgilaymiz.
Shartli ehtimollik ham Kolmogorov aksiomalarini qanoatlantiradi: 1. P ( B / A ) 0 ;
2. P ( / A ) P ( A ) P ( A ) 1 ;
P ( A ) P ( A )
3. Agar B C b o ‗ l s a , u h o l d a
P (( B C ) / A ) P (( B C ) A ) P ( B A C A ) P ( B A ) P ( C A )
P ( A ) P ( A ) P ( A )
P ( B A ) P ( C A ) P ( B / A ) P ( C / A ), P ( A ) P ( A )

chunki B C ekanligidan, ( B A ) ( C A ) B A A C B C A A
1.10-misol. Idishda 3 ta oq va 7 ta qora shar bor. Tavakkaliga ketma-ket bittadan 2 ta shar olinadi. Birinchi shar oq rangda bo‗lsa ikkinchi sharning qora rangda bo‗lishi ehtimolligini toping.
Bu misolni ikki usul bilan yechish mumkin:
1) A ={birinchi shar oq rangda}, B ={ikkinchi shar qora rangda}. A hodisa ro‗y berganidan so‗ng idishda 2 ta oq va 7 ta qora shar qoladi. Shuning
u c hun P ( B / A ) 7 .
9
formuladan
P ( A ) 3 ,
2) (1.11.1)
foydalanib,
hisoblaymiz:
10
P ( A B ) 3 7 7
1 0 9 30
Shartli ehtimollik formulasiga ko‗ra: P ( B / A ) P ( A B ) 7 / 30 7 .
P ( A ) 3 /10 9
Shartli ehtimollik formulasidan hodisalar ko‗paytmasi ehtimolligi uchun ushbu formula kelib chiqadi:
(1.11.2)
P ( A B ) P ( A ) P ( B / A ) P ( B ) P ( A / B )
(1.11.2) tenglik ko‗paytirish qoidasi(teoremasi) deyiladi. Bu qoidani n ta hodisa uchun umumlashtiramiz:
P ( A 1 A 2 ... A n ) P ( A 1 ) P ( A 2 / A 1 ) P ( A 3 / A 1 A 2 )... P ( A n / A 1 A 2 ... A n 1 ) . (1.11.3)
- Agar P ( A / B ) P ( A ) tenglik o‗rinli bo‗lsa, u holda A hodisa
B hodisaga bog‗liq emas deyiladi va A B orqali belgilanadi.
Agar A B b o ‗ l s a , u ho l da ( 1 . 1 1.2) f or m ulani qu y i d agic ha y o z i sh mumkin:
P ( A B ) P ( B ) P ( A / B ) P ( B ) P ( A ) .
- A va B hodisalar o‗zaro bog‗liq emas deyiladi, agar
P ( A B ) P ( A ) P ( B )
munosabat o‗rinli bo‗lsa.
L em m a. Agar A B b o ‗ l s a , u h o l d a A B , A B va A B b o ‗ ladi.
Isboti: A B bo‗lsin. U holda munosabat o‗rinli
P ( A B ) P ( A ) P ( B )
bo‗ladi. P ( B ) P ( B ) 1 tenglikdan foydalanib, quyidagiga ega bo‗lamiz:
P ( A B ) P ( A ( B )) P ( A A B ) P ( A A B ) P ( A ) P ( A B )
P ( A ) P ( A ) P ( B ) P ( A ) ( 1 P ( B ) ) P ( A ) P ( B ).
Demak, P ( A B ) P ( A ) P ( B ) A B . Qolganlari ham xuddi shunday isbotlanadi. ■
1.12 To‘la ehtimollik va Bayes formulalari
h od i s a lar t o ‗ la
i j . U holda
bo‗lmagan
A 1 , A 2 ,..., A n juft-jufti bilan birgalikda
A i A j ,
n
∪ A i va
gruppani tashkil etsin, ya‘ni
i 1
ol i b, B ni k o ‗ r i n ish d a y o za m i z .
ekanligini hisobga
A 1 A 2 .. . A n
B B B ( A 1 A 2 .. . A n ) B A 1 B A 2 .. . B A n
A i A j , i j ekanligidan ( B A i ) ( B A j ) , i j ekani kelib chiqadi. B
hodisaning ehtimolligini hisoblaymiz:
P ( B ) P ( B A 1 B A 2 .. . B A n )
P ( B A 1 ) P ( B A 2 ) .. . P ( B A n ) .
( 1 .1 2 .1)
K o ‗ p ay tir is h q oi d a s i g a k o ‗ ra tenglikni (1.12.1) ga qo‗llasak,
b o ‗ l a di. B u
P ( B A i ) P ( A i ) P ( B / A i ) , i 1 , n
P ( B ) P ( A 1 ) P ( B / A 1 ) P ( A 2 ) P ( B / A 2 ) ... P ( A n ) P ( B / A n ) .
- Agar B A i b o ‗ l s a , u h o ld a
i 1
n
n
P ( B ) P ( A i ) P ( B / A i )
i 1
( 1 .1 2 .2)
tenglik o‗rinli bo‗ladi. Bu tenglik to‘la ehtimollik formulas i deyiladi.
1.11-masala. Detallar partiyasi uch ishchi tomonidan tayyorlanadi. Birinchi ishchi barcha detallarning 25%ini, ikkinchi ishchi 35%ini, uchinchsi esa 40%ini tayyorlaydi. Bu uchchala ishchining tayyorlagan detallarining sifatsiz bo‗lish ehtimolliklari mos ravishda 0.05,0.04 va 0.02

ga teng bo‗lsa, tekshirish uchun partiyadan olingan detalning sifatsiz bo‗lish ehtimolligini toping.
A i = {d e tal i - i sh c hi t o m oni d a n ta yy or l a ng a n} i 1 , 3 , B = {tek s hi r ish
u c hun o li n g a n de tal s i f a t siz} ho d i s a la r n i k i r it a m iz va q u y i d a gi ehtimolliklarni hisoblaymiz:
P ( A ) 2 5 % 0 . 2 5 , P ( A ) 3 5 % 0 . 3 5 , P ( A ) 4 0 % 0 . 4 ,
3
1 2
10 0 %
10 0 % 10 0 %
P ( B / A 3 ) 0.02 . To‗la ehtimollik
P ( B / A 1 ) 0. 0 5 , P ( B / A 2 ) 0 . 0 4 ,
formulasiga asosan P ( B ) 0.25 0.05 0.35 0.04 0.4 0.02 0.0345 .
A i va B hodisalar ko‗paytmasi uchun
P ( A i B ) P ( B ) P ( A i / B ) P ( A i B ) P ( A i ) P ( B / A i )
( 1 .1 2 .3)
( 1 .1 2 .4)
tengliklar o‗rinli. (1.12.3) va (1.12.4) tengliklardan quyidagilarni hosil qilamiz:
P ( B ) P ( A i / B ) P ( A i ) P ( B / A i ) ,
P ( A i ) P ( B / A i )
P ( A / B )
. ( 1 .1 2 .5)
i
P ( B )
n
P ( B ) P ( A i ) P ( B / A i ) .
Bu yerda (1.12.5) tenglik Bayes formulasi
i 1
deyiladi. Bayes formulasi yana gipotezalar teoremasi deb ham ataladi. Agar A 1 , A 2 ,..., A n hodisalarni gipotezalar deb olsak, u holda P ( A i ) ehtimollik A i gipotezaning aprior(―a priori‖ lotincha tajribagacha), P ( A i / B ) shartli
ehtimollik esa aposterior(―a posteriori‖ tajribadan keyingi) ehtimolligi deyiladi.
1.12-masala. 1.11-misolda sifatsiz detal ikkinchi ishchi tomonidan tayyorlangan bo‗lishi ehtimolligini toping. Bayes formulasiga ko‗ra:
P ( A / B ) 0 . 3 5 0 . 04 28 0 . 4 .
2
0 . 2 5 0 . 05 0 . 3 5 0 . 04 0 . 4 0 . 02 69
1.13 Bog‘liqsiz tajribalar ketma-ketligi. Bernulli formulasi
Agar bir necha tajribalar o‗tkazilayotganida, har bir tajribada biror A hodisaning ro‗y berish ehtimolligi boshqa tajriba natijalariga bog‗liq bo‗lmasa, bunday tajribalar bog‗liqsiz tajribalar deyiladi.
n ta bog‗liqsiz tagribalar o‗tkazilayotgan bo‗lsin. Har bir tajribada A
hodisaning ro‗y berish ehtimolligi P ( A ) p va ro‗y bermasligi ehtimolligi
P ( A ) 1 p q b o ‗ l s i n .
Masalan, 1) nishonga qarata o‗q uzish tajribasini ko‗raylik. Bu yerda A ={o‗q nishonga tegdi}-muvaffaqqiyat va A ={o‗q nishonga tegmadi}- muvaffaqqiyatsizlik; 2) n ta mahsulotni sifatsizlikka tekshirilayotganda A ={mahsulot sifatli}-muvaffaqqiyat va A ={mahsulot sifatsiz}- muvaffaqqiyatsizlik bo‗ladi.
Bu kabi tajribalarda elementar hodisalar fazosi faqat ikki
e l e m e nt d a n i b orat b o ‗ ladi: { 0 , 1 } { A , A } , bu e r d a 0 - A hod i sa r o ‗ y bermasligini, 1 - A hodisa ro‗y berishini bildiradi. Bu hodisalarning ehtimolliklari mos ravishda p va q (p+q=1) lar orqali belgilanadi.
Agar n ta tajriba o‗tkazilayotgan bo‗lsa, u holda elementar hodisalar fazosining elementar hodisalari soni 2 n ga teng bo‗ladi. Masalan, n=3 da
{ 0 , 1 ,..., 7 } { AAA , AAA , AAA , AAA , AAA , AAA , AAA , AAA } , ya‘ni
to‗plam 2 3 =8 ta elementar hodisadan iborat. Har bir ehtimolligini ko‗paytirish teoremasiga ko‗ra hisoblash mumkin:
hodisaning
p ( 0 ) P ( A A A ) P ( A ) P ( A ) P ( A ) q ,
3
p ( 1 ) P ( A A A ) P ( A ) P ( A ) P ( A ) p q ,
2
........ . ....... . ....... . ....... . ....... . ....... . ...
p ( 7 ) P ( AA A ) P ( A ) P ( A ) P ( A ) p .
3
n ta bog‗liqsiz tajribada A hodisa m marta ro‗y berish ehtimolligini hisoblaylik:
P n ( m ) P ( A – A . – .. A A – A . – .. A ) P ( A A – A . – .. A A – A . – .. A ) ...
mta ( n m ) ta mta ( n ( m 1)) ta
P ( A – A . – .. A A – A . – .. A A ) P ( A – A . – .. A A – A . – .. A ).
( n ( m 1)) ta mta ( n m ) ta mta
p m q n m
Har bir qo‗shiluvchi ko‗paytirish teoremasiga ko‗ra Demak,
ga teng.
m 0 ,1 ,.. . n
P ( m ) p m q n m p m q n m ... p m q n m C m p m q n m ,
.
––––––––––
n
n
C m ta qo ' shiluvchi
n
- Agar n ta bo‗g‗liqsiz tajribaning har birida A hodisaning ro‗y berish ehtimolligi p ga, ro‗y bermasligi q ga teng bo‗lsa, u holda A hodisaning m marta ro‗y berish ehtimolligi quyidagi ifodaga teng bo‗ladi:
m 0 , 1 ,.. . n .
P ( m ) C m p m q n m ,
( 1 .1 3 . 1 )
n n
(1.13.1) formula Bernulli formulasi deyiladi. P n ( m ) ehtimolliklar uchun
P n ( m ) 1 tenglik o‗rinlidir. Haqiqatan ham,
m 0
n
( q px ) n q n C 1 q n 1 px C 2 q n 2 p 2 x 2 ... p n x n
n n
N y ut o n b i no m i fo r m ulasi d a x 1 d e b o l s a k,
n n 1 n 1 2 n 2 2 n
, ya‘ni
( q p ) q C q p C q p .. . p
n n
1 P n (0) P n (1) ... P n ( n ) P n ( m ) bo‗ladi.
m 0
(1.13.1) ehtimolliklar xossalari:
1. P n ( m ) 1 .
n
n
m 0
m 2
- Agar m 1 m m 2 b o ‗ l s a , P n ( m 1 m m 2 ) P n ( m ) .
m m 1
- n ta bog‗liqsiz tajribada A hodisaning kamida 1 marta ro‗y berishi ehtimolligi P 1 q n bo‗ladi.
C hu n ki, P ( 0 ) 1 q .
n
P ( 0 ) P (1 ) . . . P ( n ) 1 P 1
n – – – – n
n
n
P
4. Agar P n ( m ) ehtimollikning eng katta qiymati P n ( m 0 ) bo‗lsa, u holda m 0
qu y i d ag icha a ni q la n a di: m 0 - e ng eh ti m olli s on deyiladi va
n p q m 0 ( n 1 ) p ,
- agar np-q kasr son bo‗lsa, u holda m 0 yagonadir;
- agar np-q butun son bo‗lsa, u holda m 0 ikkita bo‗ladi.

1.13-misol. Ikki teng kuchli shaxmatchi shaxmat o‗ynashmoqda. Qaysi hodisaning ehtimolligi katta: 4 ta partiyadan 2 tasida yutishmi yoki 6
ta partiyadan 3 tasida yutish. Birinchi holda: n =4, m =2, p = 1 , Bernulli
2
1 4 2
1 1 6
1 2
formulasiga ko‗ra
.
2
P ( 2 ) C 1
6
2 2 2 2
va Bernulli formulasiga ko‗ra
4
2
16
4 2
I k k i n c hi h ol d a n = 6, m = 3, p = 1
2
1 6 3
6 5
1 1 5
1 3
P 4 ( 2) P 6 ( 3 ) . Dem a k, 4
.
3
2 0
P (3) C 1
2 3 2 3
6
2 16 16 16
6 2
ta partiyadan 2 tasida yutish ehtimolligi katta ekan.
1.14 Limit teoremalar
Agar n va m lar katta sonlar bo‗lsa, u holda Bernulli formulasidan foydalanib, P n ( m ) ehtimollikni hisoblash qiyinchilik tug‗diradi. Xuddi shunday, p ( q ) ehtimollik juda kichik qiymatlar qabul qilsa ham qiyinchiliklarga duch kelamiz. Shu sababli, n da P n ( m ) uchun asimptotik(taqribiy) formulalar topish muammosini tug‗diradi.
Puasson formulasi
- Agar n da A hodisaning ro‗y berish ehtimolligi p har bir tajribada cheksiz kamaysa(ya‘ni np a 0 ), u holda
a m e a
li m P n ( m )
, m =0,1,2,… .
( 1 .1 4 . 1 )
m !
n
(1.14.1) formula Puassonning asimptotik formulasi deyiladi.
p a belgilash kiritib, Bernulli formulasidan
n
a n m
n ! a m
P ( m ) C m p m q n m
1
n n
m ! ( n m ) ! n n
a m
n ( n 1 ) . . . ( n ( m 1 ) ) a m
a n
1
1
m
n
n
m ! n

a m
a m
n n 1 n 2
n ( m 1 ) a n
1 1
. . .
n n
n
m ! n n n
a m
a m
1 2 m 1 a n
1 1 1 . . . 1
1 1
(1.14.2)
m ! n
n
n
n
n
a n
e a
ekanligini e‘tiborga olib, (1.14.2) tenglikdan limitga
l i m 1
n
n
o‗ ta m iz:
a m
a
.
lim P n ( m ) e
m !
n
Demak, yetarlicha katta n larda (kichik p da)
a m e a
P n ( m )
, a np , m 0,1,..., n
( 1 . 1 4. 3 )
m !
(1.14.3) formula Puasson formulasi deyiladi. Odatda Puasson formulasidan
n 5 0 , n p 1 0 b o ‗ l g a n h oll ar da fo y d a laniladi.
1.14-misol. Telefon stansiyasi 2000 ta abonentga xizmat ko‗rsatadi. Agar har bir abonent uchun unig bir soatning ichida qo‗ng‗iroq qilishi ehtimolligi 0.003 bo‗lsa, bir soatning ichida 5 ta abonent qo‗ngiroq qilishi ehtimolligini toping.
n =2000, p =0.003, m =5, a=np= 2000 0.003=6
6 5 e 6
0 , 1 3 .
formulasiga ko‗ra P 2000 (5)
5 !
Muavr-Laplasning lokal teoremasi
Agar p ( p 0, p 1 )ehtimollik nol atrofidagi son bo‗lmasa va n etarlicha katta bo‗lsa, u holda P n ( m ) ehtimollikni hisoblash uchun Muavr- Laplas teoremasidan foydalanish mumkin.
Teorema(Muavr-Laplas) Agar n ta bog‗liqsiz tajribada A
hodisaning ro‗y berish ehtimolligi 0 p 1 bo‗lsa, u holda yetarlicha katta
n larda
- x 2
1 1
2 , x m np
P n ( m ) e
( 1 .1 4 . 4 )
n p q 2
npq
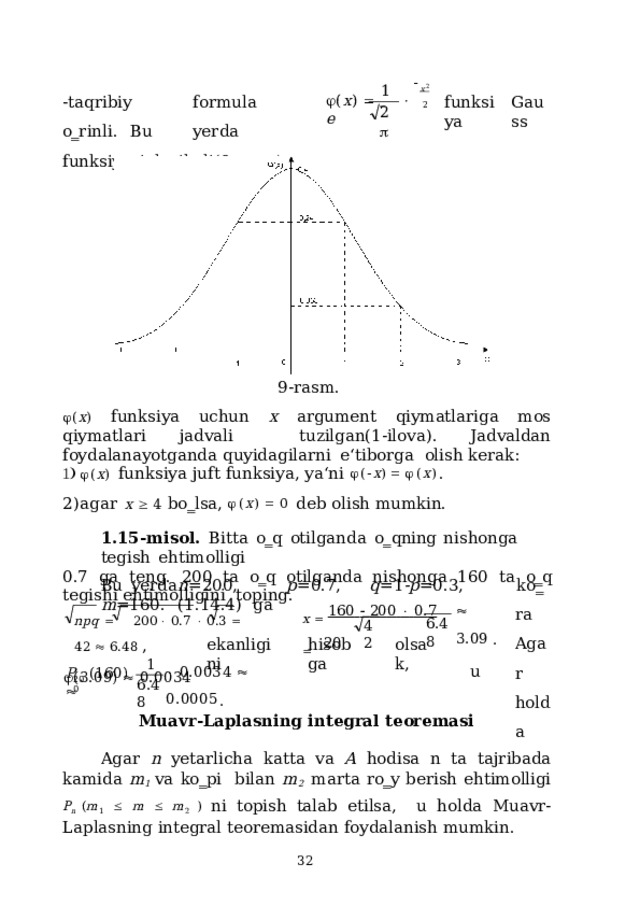
- x 2
2
1
- taq r i biy for m ula o‗ r i n l i. B u ye r d a funksiyasi deyiladi(9-rasm).
( x ) e
G a u ss
funksiya
2
9-rasm.
( x ) funksiya uchun x argument qiymatlariga mos qiymatlari jadvali tuzilgan(1-ilova). Jadvaldan foydalanayotganda quyidagilarni e‘tiborga olish kerak:
- ( x ) f u n k siya juft f u n ksiy a , ya ‘ n i ( x ) ( x ) .
- agar x 4 bo‗lsa, ( x ) 0 deb olish mumkin.
1.15-misol. Bitta o‗q otilganda o‗qning nishonga tegish ehtimolligi
0.7 ga teng. 200 ta o‗q otilganda nishonga 160 ta o‗q tegishi ehtimolligini toping.
k o ‗ ra Agar ho l d a
Bu yerda n =200, p =0.7, q =1 -p =0.3, m =160. (1.14.4) ga
np q 20 0 0 . 7 0 . 3 4 2 6 . 4 8 ,
(3.09) 0.0034
x 16 0 20 0 0. 7 20
3. 0 9 .
u
6. 48
42
ekanligini
hisobga
o l s a k,
1
0 . 003 4 0 . 000 5 .
P (160)
200
6 . 48
Muavr-Laplasning integral teoremasi
Agar n yetarlicha katta va A hodisa n ta tajribada kamida m 1 va ko‗pi bilan m 2 marta ro‗y berish ehtimolligi P n ( m 1 m m 2 ) ni topish talab etilsa, u holda Muavr-Laplasning integral teoremasidan foydalanish mumkin.
![Teorema(Muavr-Laplas) Agar A ehtimolligi( 0 p 1 ) o‗zgarmas bo‗lsa, u holda hodisaning ro‗y berish x 2 1 2 e x 2 dx P n ( m 1 m m 2 ) , ( 1 .1 4 . 5 ) 2 x 1 m np taqribiy formula o‗rinli, bu yerda x , i 1 , 2 . i i n pq (1.14.5) formuladan foydalanilganda hisoblashlarni soddalashtirish uchun maxsus funksiya kiritiladi: 1 2 x 0 2 e t 2 dt ( x ) . ( 1 .1 4 . 6 ) 0 (1.14.6)-Laplas funksiyasi deyiladi. 10-rasm. 0 ( x ) funksiya toq funksiya: x x 1 1 2 e t 2 d t [ t z ] 2 z ( x ) e dz ( x ) 0 . 2 0 2 2 0 0 Agar x 5 bo‗lsa, u holda 0 ( x ) 0.5 deb hisoblash mumkin; 0 ( x ) f u n k s iya g r a f i gi 1 0 - ras m da keltir i l g a n. (1.14.5) dagi tenglikning o‗ng qismini 0 ( x ) funksiya orqali ifodalaymiz:](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img32.jpg)
Teorema(Muavr-Laplas) Agar A ehtimolligi( 0 p 1 ) o‗zgarmas bo‗lsa, u holda
hodisaning ro‗y berish
x 2
1
2
e x 2 dx
P n ( m 1 m m 2 )
,
( 1 .1 4 . 5 )
2
x 1
m np
taqribiy formula o‗rinli, bu yerda x
, i 1 , 2 .
i
i
n pq
(1.14.5) formuladan foydalanilganda hisoblashlarni soddalashtirish uchun maxsus funksiya kiritiladi:
1
2
x
0
2
e t 2 dt
( x )
. ( 1 .1 4 . 6 )
0
(1.14.6)-Laplas funksiyasi deyiladi.
10-rasm.
0 ( x ) funksiya toq funksiya:
x
x
1
1
2
e t 2 d t [ t z ]
2
z
( x )
e dz ( x )
0 .
2
0
2
2
0 0
Agar x 5 bo‗lsa, u holda 0 ( x ) 0.5 deb hisoblash mumkin;
0 ( x ) f u n k s iya g r a f i gi 1 0 - ras m da keltir i l g a n.
(1.14.5) dagi tenglikning o‗ng qismini 0 ( x ) funksiya orqali ifodalaymiz:
x 2
1
- x
e 2 dx
P n ( m 1 m m 2 )
2
x 1
1
2
x 2
x 2
0
0
1
1
t
- x
- x
e 2 dt
e 2 d x
e dx ( x ) ( x ). (1.14.7)
2
2
2
0 2 0 1
x 1
x 1
1
2
x
2
e t 2 dt
( x )
-Laplasning funksiyasi bilan bir qatorda Gauss
0
0
funksiyasi deb nomlanuvchi funksidan ham foydalaniladi:
1
2
x
2
e t 2 dt
( x )
.
(1.14.8)
Bu funksiya uchun ( x ) ( x ) 1 tenglik o‗rinli va u 0 ( x ) funksiya bilan
( x ) 0. 5 0 ( x )
formula orqali bog‗langan.
1.16-misol. Sex ishlab chiqargan mahsulotining o‗rtacha 96% i sifatli. Bazada mahsulotni qabul qilib oluvchi sexning 200 ta mahsulotini tavakkaliga tekshiradi. Agar tekshirilgan mahsulotlardan sifatsizlari soni
10 tadan ko‗p bo‗lsa butun mahsulotlar partiyasi sifatsiz deb, sexga qaytariladi. Mahsulotlar partiyasining qabul qilinishi ehtimolligini toping. Bu yerda n =200, p =0.04(mahsulotning sifatsiz bo‗lish ehtimolligi), q =0.96, m 1 =0, m 2 =10 va mahsulotlar partiyasining qabul qilinishi ehtimolligi
P 200 (0 m 10) ni (1.14.7) formula orqali hisoblaymiz:
( 1 .1 4 . 9 )
x 0 20 0 0. 0 4 2. 8 9 , 1 0 20 0 0 . 0 4 0. 7 2 ,
x
1
2
20 0 0. 0 4 0. 9 6 20 0 0. 0 4 0. 96
P 200 (0 m 10) 0 (0.72) 0 ( 2.89) 0.26424 0.49807 0.7623 .
Agar funksiyadan foydalansak,
( x )
P 200 ( 0 m 1 0 ) (0 . 7 2 ) ( 2 . 8 9 )
0.7642 (1 (2.89)) 0.7642 (1 0.998074) 0.7623 .
L a p las f u n k s iy a s i y or d a m i d a n ta bo g ‗ l i q s iz taj r i b a da nisbiy chastotaning ehtimollikdan chetlashishi ehtimolligini hisoblash mumkin.
- Biror 0 son uchun

n
n A
pq
P n p 2 0
( 1 .1 4 . 1 0)
tenglik o‗rinli.
Haqiqatan ham, buni isbotlash uchun hiso b la s h k e ra k . B uning u c h u n bu
n A
n
p
tengsizlik ehtimolligini
ten g s izlikni u ng a teng k u c hli
n A p yoki n A np tengsizliklar bilan almashtiramiz. Bu
n
n
songa ko‗paytiramiz:
tengsizliklarni musbat
n pq
n n A np n .
p q pq
npq
Agar m n A np belgilashni kiritsak, u holda (1.14.5) formulaga asosan:
n p q
n
n
n p q
n p q
p q
p q
n
2
1
2
2
0
m
P (
e t 2 d t 2
)
.
e t 2 d t
0
n
pq
2
2
n
pq
■
1.17-misol. Detalning nostandart bo‗lishi ehtimolligi 0.6 ga teng.
n =1200 ta detal ichida nostandart detallar bo‗lishi nisbiy chastotasining
0.05 d a n k a tta
p = 0.6 e hti m ollikdan c h e tl a s h ishi a b s olut qiy m a ti bo‗lmasligi ehtimolligini toping.
(1.4.10) ga asosan,
n A
12 0 0
2 (3.54) 0.9996
P
0 . 6 0 . 0 5 2 0 0 . 05
0.6 0.4 0 .
1 2 00
n
I bobga doir misollar
isb o t lan g : a )
1. A , B va С hodisalar uchun quyidagilarni
B A B A B ;
b) ( A B ) ( B C ) A B C ; c ) A B A B .
2. 1 1 -ras m da 6 e le me nt d a n ibo r a t s x e m a b e r i l g a n. A i ( i 1 ,6 ) hodisalar ma‘lum T vaqt oralig‗ida mos elementlarning beto‗xtov ishlashi
![bo‗lsa, bu hodisalar orqali ma‘lum T vaqt oralig‗ida sxemaning beto‗xtov ishlashini ifodalang. 11-rasm. Ixtiyoriy ikki qo‗shni raqamlari har xil bo‗lgan nechta to‗rt xonali son hosil qilish mumkin? Musobaqaning 10 ta ishtirokchisiga 3 ta yutuqni necha xil usul bilan taqsimlash mumkin. Ma‘lum uchta kitob yonma-yon turadigan qilib, 7 ta kitobni tokchaga necha xil usul bilan taxlash mumkin. Birinchi talabada 7 xil, ikkinchisida 16 xildagi kitoblar bor bo‗lsa, kitobga kitobni necha xil usul bilan almashtirishlari mumkin. 2 ta kitobga 2 ta kitobnichi? 3,3,5,5,8 raqamlaridan nechta besh xonali son hosil qilish mumkin. 9 qavatli bino liftiga 4 kishi kirdi. Ularning har biri bir-biriga bo‗gliqsiz ravishda ixtiyoriy qavatda chiqishlari mumkin. Ular : a) turli qavatlarda; b) bitta qavatda: c) 5-qavatda chiqishlari ehtimolliklarini toping. Imtihon biletlariga kiruvchi 60 savoldan talaba 50 tasini biladi. Tavakkaliga tanlangan 3 ta savoldan: a) hammasini; b) ikkitasini bilishi ehtimolligini toping. Idishda 5 ta ko‗k, 4 ta qizil va 3 ta yashil shar bor. Tavakkaliga olingan 3 ta sharning: a) bir xil rangda; b) har xil rangda; c) 2 tasi ko‗k va 1 tasi yashil rangda bo‗lishi ehtimolligini hisoblang. R radiusli doiraga teng tomonli uchburchak ichki chizilgan. Doiraga tavakkaliga tashlangan nuqtaning uchburchakka tushishi ehtimolligini toping. [0,5] kesmadan tavakkaliga bitta nuqta tanlanadi. Shu nuqtadan kesmaning o‗ng oxirigacha bo‗lgan masofa 1.6 birlikdan oshmasligi ehtimolligini toping.](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img35.jpg)
bo‗lsa, bu hodisalar orqali ma‘lum T vaqt oralig‗ida sxemaning beto‗xtov ishlashini ifodalang.
11-rasm.
- Ixtiyoriy ikki qo‗shni raqamlari har xil bo‗lgan nechta to‗rt xonali son hosil qilish mumkin?
- Musobaqaning 10 ta ishtirokchisiga 3 ta yutuqni necha xil usul
bilan taqsimlash mumkin.
- Ma‘lum uchta kitob yonma-yon turadigan qilib, 7 ta kitobni tokchaga necha xil usul bilan taxlash mumkin.
- Birinchi talabada 7 xil, ikkinchisida 16 xildagi kitoblar bor bo‗lsa,
kitobga kitobni necha xil usul bilan almashtirishlari mumkin. 2 ta kitobga 2 ta kitobnichi?
- 3,3,5,5,8 raqamlaridan nechta besh xonali son hosil qilish mumkin.
- 9 qavatli bino liftiga 4 kishi kirdi. Ularning har biri bir-biriga bo‗gliqsiz ravishda ixtiyoriy qavatda chiqishlari mumkin. Ular : a) turli qavatlarda; b) bitta qavatda: c) 5-qavatda chiqishlari ehtimolliklarini toping.
- Imtihon biletlariga kiruvchi 60 savoldan talaba 50 tasini biladi. Tavakkaliga tanlangan 3 ta savoldan: a) hammasini; b) ikkitasini bilishi ehtimolligini toping.
- Idishda 5 ta ko‗k, 4 ta qizil va 3 ta yashil shar bor. Tavakkaliga
olingan 3 ta sharning: a) bir xil rangda; b) har xil rangda; c) 2 tasi ko‗k va 1 tasi yashil rangda bo‗lishi ehtimolligini hisoblang.
- R radiusli doiraga teng tomonli uchburchak ichki chizilgan. Doiraga tavakkaliga tashlangan nuqtaning uchburchakka tushishi
ehtimolligini toping.
- [0,5] kesmadan tavakkaliga bitta nuqta tanlanadi. Shu nuqtadan kesmaning o‗ng oxirigacha bo‗lgan masofa 1.6 birlikdan oshmasligi ehtimolligini toping.

- Idishda 4 ta oq, 3 ta ko‗k va 2 ta qora shar bor. Tavakkaliga, ketma-ket, bittadan 3 ta shar olindi. Birinchi shar oq, ikkinchisi ko‗k va uchinchisi qora rangda bo‗lishi ehtimolligini toping.
- Shoshqol toshni tashlash tajribasida A ={juft raqam tushishi} va B ={3 dan katta raqam tushishi} hodisalari bo‗lsin. A va B hodisalar bog‗liqsizmi?
- Quyida berilgan bir-biriga bog‗liqsiz ravishda ishlaydigan
elementlardan iborat sxemaning safdan chiqishi ehtimolligini toping,
i ( i =1,2,…,7)-elementning safdan chiqishi ehtimolligi 0.2 ga teng .
12-rasm.
- Asbob ikki mikrosxemadan iborat. Birinchi mikrosxemaning 10 yil ichida ishdan chiqishi ehtimolligi 0.07, ikkinchisiniki-0.10. Bitta mikrosxema ishdan chiqgani ma‘lum bo‗lsa, bu mikrosxema birinchisi ekanligi ehtimolligini toping.
- Talaba imtihon 40 ta biletlarining faqat 30 tasiga javob bera oladi. Talabaga imtihonga birinchi bo‗lib kirishi foydalimi, yoki ikkinchi?
- Zavod ishlab chiqargan mahsulotning 90% i sifat talablariga
javob beradi. Tekshruvchi mahsulotni 0.96 ehtimollik bilan sifatli, 0.06 ehtimollik bilan sifatsiz deb topadi. Tavakkaliga olingan mahsulotning sifatli deb topilishi ehtimolligini toping.
- Oilada 3 ta farzand bor. Agar o‗g‗il bola tug‗ilishi ehtimolligi
0.51, qiz bola tug‗lishi ehtimolligi 0.49 ga teng bo‗lsa, a) bolalarning hammasi o‗g‗illar, b) 1 tasi o‗g‗il va 2 tasi qiz bo‗lishi ehtimolliklarini hisoblang.
20. Shoshqol tosh 10 marta tashlanganda:
- 6 raqami bir marta tushishi ehtimolligini;
- 6 raqami kamida bir marta tushish ehtimolligini;

- 6 raqami tushishi soni ehtimolligi maksimal qiymatga erishadigan miqdorni toping.
- ― Ehtimollar nazariyasi‖ fanidan ma‘ruza darsida 84 ta talaba
- ― Ehtimollar nazariyasi‖ fanidan ma‘ruza darsida 84 ta talaba
ishtirok etmoqda. Shu talabalarning ikkitasini tug‗ilgan kuni shu kuni bo‗lishi ehtimolligini toping.
- Mahsulotning sifatsiz bo‗lishi ehtimolligi 0.02 ga teng. 200 ta mahsulotning ichida sifatsizlari bittadan ko‗p bo‗lmasligi ehtimolligiti
- Mahsulotning sifatsiz bo‗lishi ehtimolligi 0.02 ga teng. 200 ta mahsulotning ichida sifatsizlari bittadan ko‗p bo‗lmasligi ehtimolligiti
toping.
- A hodisaning ro‗y berish ehtimolligi 0.6 ga teng. 100 ta bog‗liqsiz tajribada A hodisaning 70 marta ro‗y berishi ehtimolligini toping. Shunday m sonini topingki, 0.95 ehtimollik bilan 800 ta yangi tug‗ilgan chaqaloqlardan kamida m tasi qizlar deb aytish mumkin bo‗lsin. Qiz bola tug‗ilishi ehtimolligini 0.485 deb hisoblang.
- A hodisaning ro‗y berish ehtimolligi 0.6 ga teng. 100 ta bog‗liqsiz tajribada A hodisaning 70 marta ro‗y berishi ehtimolligini toping.
- Shunday m sonini topingki, 0.95 ehtimollik bilan 800 ta yangi tug‗ilgan chaqaloqlardan kamida m tasi qizlar deb aytish mumkin bo‗lsin. Qiz bola tug‗ilishi ehtimolligini 0.485 deb hisoblang.
- Detalning nostandart bo‗lishi ehtimolligi 0.1 ga teng. Tavakkaliga olingan 400 ta detal ichida nostandart detallar bo‗lishi nisbiy chastotasining p=0.1 ehtimollikdan chetlashishi absolut qiymati 0.03 dan katta bo‗lmasligi ehtimolligini toping.
- Detalning nostandart bo‗lishi ehtimolligi 0.1 ga teng. Tavakkaliga olingan 400 ta detal ichida nostandart detallar bo‗lishi nisbiy chastotasining p=0.1 ehtimollikdan chetlashishi absolut qiymati 0.03 dan katta bo‗lmasligi ehtimolligini toping.
II bob Tasodifiy moqdorlar
2.1 Tasodifiy miqdor tushunchasi
Ehtimollar nazariyasining muhim tusunchalaridan biri tasodifiy miqdor tushunchasidir.
- Tajriba natijasida u yoki bu qiymatni qabul qilishi oldindan ma‘lum bo‗lmagan miqdor tasodifiy miqdor deyiladi.
Tasodifiy miqdorlar lotin alifbosining bosh harflari X , Y , Z ,…(yoki grek
alifbosining kichik harflari (ksi), (eta), δ(dzeta),…) bilan qabul qiladigan qiymatlari esa kichik harflar x 1 , x 2 ,..., y 1 , y 2 ,... , z 1 , z 2 ,... bilan belgilanadi.
Tasodifiy miqdorlarga misollar keltiramiz: 1) X -tavakkaliga olingan mahsulotlar ichida sifatsizlari soni; 2) Y - n ta o‗q uzilganda nishonga tekkanlari soni; 3) Z -asbobning beto‗htov ishlash vaqti; 4) U -[0,1] kesmadan tavakkaliga tanlangan nuqtaning koordinatalari; 5) V -bir kunda tug‗iladigan chaqaloqlar soni va h.k..
- Agar tasodifiy miqdor(t.m.) chekli yoki sanoqli qiymatlar qabul qilsa, bunday t.m. diskret tipdagi t.m. deyiladi.
- Agar t.m. qabul qiladigan qiymatlari biror oraliqdan iborat bo‗lsa
uzluksiz tipdagi t.m. deyiladi.
Demak, diskret t.m. bir-biridan farqli alohida qiymatlarni, uzluksiz t.m. esa biror oraliqdagi ihtiyoriy qiymatlarni qabul qilar ekan. Yuqoridagi X va Y t.m.lar diskret, Z esa uzluksiz t.m. bo‗ladi.
Endi t.m.ni qat‘iy ta‘rifini keltiramiz.
- elementar hodisalar fazosida aniqlangan X sonli funksiya t.m. deyiladi, agar har bir elementar hodisaga X ( ) conni mos qo‗ysa, yani X = X ( ), .
Masalan, tajriba tangani 2 marta tashlashdan iborat bo‗lsin. Elementar
{ 1 , 2 , 3 , 4 }, 1 G G , 2 G R , 3 R G , 4 R R
ho d i s a lar fa z o s i
bo‗ladi. X-gerb chiqishlari soni bo‗lsin, u holda X t.m. qabul qiladigan qiymatlari: X ( 1 )=2, X ( 2 )=1, X ( 3 )=1, X ( 4 )=0.
Agar chekli yoki sanoqli bo‗lsa, u holda da aniqlangan ixtiyoriy funksiya t.m. bo‗ladi. Umuman, X ( ) funksiya shunday bo‗lishi kerakki:
x R da A { : X ( ) x } hodisa S - algebrasiga tegishli bo‗lishi kerak.
2.2 Diskret tasodifiy miqdorning taqsimot qonuni
x 1 , x 2 , ..., x n , ...
X -d iskr e t t. m . b o ‗ l s i n. X t. m . qiy ma tl a r n i m o s
p 1 , p 2 ,..., p n ,... ehtimolliklar bilan qabul qilsin:
X
P
x 1
p 1
x 2
…
p 2
…
x n
…
p n
…
jadval diskret t.m. taqsimot qonuni jadvali deyiladi. Diskret t.m. taqsimot qonunini p i P { X x i }, i 1, 2,..., n ,... ko‗rinishda yozish ham qulay.
{ X x 1 }, { X x 2 },... hodisalar birgalikda bo‗lmaganligi uchun ular to‗la gruppani tashkil etadi va ularning ehtimolliklari yig‗indisi birga teng
b o ‗ lad i , ya ‘ni p i P { X x i } 1 .
i i
- X t.m. diskret t.m. deyiladi, agar x 1 , x 2 ,... chekli yoki sanoqli to‗plam bo‗lib, P { X x i } p i 0 ( i 1, 2,...) va p 1 p 2 ... 1 tenglik o‗rinli bo‗lsa.
A i { X x i }
- X va Y d i skret t .m . l a r bog ‘ l iqsiz d e y il a di, a g a r va
B i { Y y j } hodisalar i 1, 2,..., n , j 1, 2,..., m da bog‗liqsiz bo‗lsa, ya‘ni
P { X x i , Y y j } P { X x i } P { Y y j } , n , m .
2.1-misol. 10 ta lotoreya biletida 2 tasi yutuqli bo‗lsa, tavakkaliga olingan 3 ta lotoreya biletlari ichida yutuqlilari soni X t.m.ning taqsimot qonunini toping.
X t.m.ni qabul qilishi mumkin bo‗lgan qiymatlari x 1 0, x 2 1, x 3 2 . Bu
qiymatlarning mos ehtimolliklari esa
C 0 C 3 56 7
;
p P { X 0} 2 8
C 3
1
12 0 1 5
10
C 1 C 2
5 6 7
;
p P { X 1} 2 8
C 3
2
12 0 1 5
10
C 2 C 1 8 1
p P { X 2} 2 8
.
C 3
3
12 0 1 5
10
X t.m. taqsimot qonunini jadval ko‗rinishida yozamiz:
X
0
P
1
7
7
15
2
15
1
15
p 7 7
3
i 1
1 1
i
15 15 15

2.3 Taqsimot funksiyasi va uning xossalari
Diskret va uzluksiz t.m.lar taqsimotlarini berishning universal usuli ularning taqsimot funksiyalarini berishdir. Taqsimot funksiya F ( x ) orqali belgilanadi.
- F ( x ) funksiya X t.m.ning taqsimot funksiyasi x R son uchun quyidagicha aniqlanadi:
F ( x ) P { X x } P { : X ( ) x } . (2.3.1)
Taqsimot funksiyasi quyidagi xossalarga ega:
- F ( x ) chegaralangan:
0 F ( x ) 1 .
- F ( x ) kamaymaydigan funksiya: agar x 1 x 2 bo‗lsa, u holda
F ( x 1 ) F ( x 2 ) .
F ( ) l i m F ( x ) 0 , F ( ) l i m F ( x ) 1 .
x x
3.
4. F ( x ) funksiya chapdan uzluksiz:
l i m F ( x ) F ( x 0 ) .
x x 0 0
Isboti: 1. Bu xossa (2.3.1) va ehtimollikning xossalaridan kelib chiqadi.
2. hodisalarni kiritamiz. Agar x 1 x 2 bo‗lsa, u
A { X x 1 }, B { X x 2 }
ho l da A B va P ( A ) P ( B ) , ya ‘ n i y o ki
P ( X x 1 ) P ( X x 2 )
F ( x 1 ) F ( x 2 ) .
- { X } va { X } ekanligi va ehtimollikning xossasiga ko‗ra
F ( ) P { X } P { } 0
F ( ) P { X } P { } 1 .
- A { X x 0 }, A n { X x n } hodisalarni kiritamiz. Bu yerda { x n } ketma- ketlik monoton o‗suvchi, x n x 0 . A n hodisalar ketma-ketligi ham o‗suvchi bo‗lib, A n A . U holda P ( A n ) P ( A ) , ya‘ni lim F ( x ) F ( x 0 ) . ■
x x 0
n
 2 b o ‗ l s a , F ( x ) P { X 0 } P { X 1 } P { X 2 } 7 7 1 1 . 1 5 1 5 1 5 De m a k, 0, agar x 0 7 , a g ar 0 x 1 F ( x ) 15 1 4 1 5 , a g ar 1 x 2 1 , a g ar x 2 F ( x ) taqsimot funksiya grafigi 13-rasmda keltirilgan. 13 -ras m . " width="640"
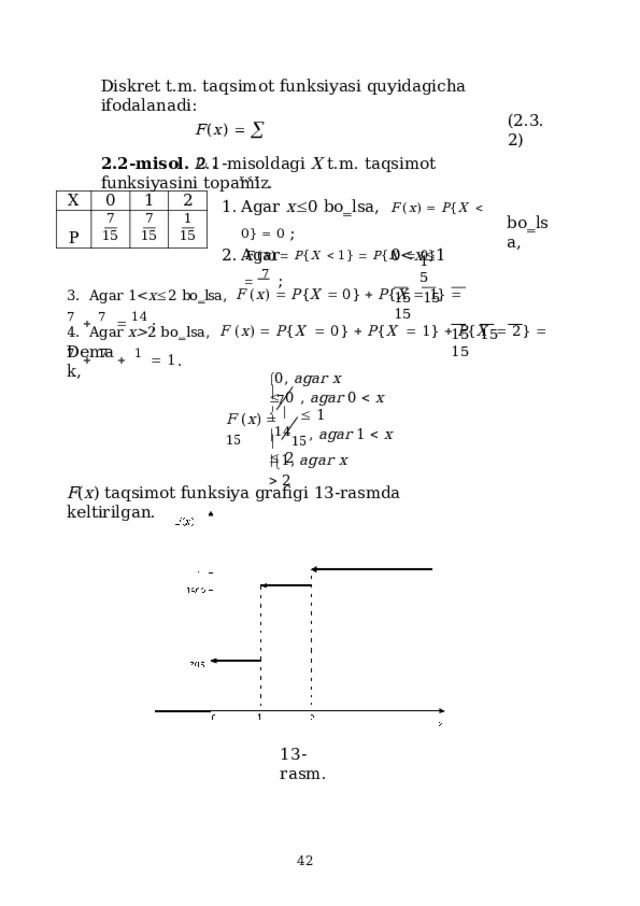
2 b o ‗ l s a , F ( x ) P { X 0 } P { X 1 } P { X 2 } 7 7 1 1 . 1 5 1 5 1 5 De m a k, 0, agar x 0 7 , a g ar 0 x 1 F ( x ) 15 1 4 1 5 , a g ar 1 x 2 1 , a g ar x 2 F ( x ) taqsimot funksiya grafigi 13-rasmda keltirilgan. 13 -ras m . " width="640"
Diskret t.m. taqsimot funksiyasi quyidagicha ifodalanadi:
F ( x ) p i .
x i x
(2.3.2)
2.2-misol. 2.1-misoldagi X t.m. taqsimot funksiyasini topamiz.
- Agar x 0 b o ‗ l s a , F ( x ) P { X 0 } 0 ;
- Agar 0x 1
X
0
P
7
1
15
7
2
1
15
15
b o ‗ ls a ,
F ( x ) P { X 1 } P { X 0 } 7 ;
15
3. Agar 1x 2 bo‗lsa, F ( x ) P { X 0} P { X 1} 7 7 14 ;
1 5 1 5 1 5
4 . Agar x 2 b o ‗ l s a , F ( x ) P { X 0 } P { X 1 } P { X 2 } 7 7 1 1 .
1 5 1 5 1 5
De m a k,
0, agar x 0
7
, a g ar 0 x 1
F ( x ) 15
1 4 1 5 , a g ar 1 x 2
1 , a g ar x 2
F ( x ) taqsimot funksiya grafigi 13-rasmda keltirilgan.
13 -ras m .
- X t.m. uzluksiz deyiladi, agar uning taqsimot funksiyasi ixtiyoriy nuqtada uzluksiz bo‗lsa.
Agar F ( x ) taqsimot funksiya uzluksiz t.m. taqsimot funksiyasi bo‗lsa,
taq si m ot fun k s iy an i n g 1 - 4 x o s s a larid a n qu y i d ag i n a t i jal a r n i k e lti ri sh mimkin:
- X t.m.ning [a,b) oraliqda yotuvchi qiymatni qabul qilish ehtimolligi taqsimot funksiyaning shu oraliqdagi orttirmasiga teng:
P { a X b } F ( b ) F ( a ) . (2.3.3)
- X uzluksiz t.m.ning tayin bitta qiymatni qabul qilishi ehtimolligi nolga teng:
P { X x i } 0
1-natijada [ a,b ], ( a,b ], ( a,b ) oraliqlar uchun ham (2.3.3) tenglik o‗rinli, ya‘ni
P { a X b } P { a X b } P { a X b } P { a X b } F ( b ) F ( a ) . M a s a lan, P { a X b } P { X a } P { a X b } P { a X b } .
Isboti. 1. a bo‗lgani uchun { X b } { X a } { a X b } . { X a } va
{ a X b } hod i s a lar bi r g a li k da b o ‗ l m a g a ni u c hun P { X b } P { X a }
P { a X b } . P { a X b } P { X b } P { X a } F ( b ) F ( a ) .
2. (2.3.3.) tenglikni [ a,x ) oraliqqa tatbiq etamiz: P { a X x } F ( x ) F ( a ) .
F ( x ) funk s iya a n u qtada u zl u k s i z b o ‗ l g a ni u ch un
l i m F ( x ) F ( a ) .
x a
lim P { a X x } P { X a } lim F ( x ) F ( a ) F ( a ) F ( a ) 0 .
x a x a
■
2.4 Zichlik funksiyasi va uning xossalari
Uzluksiz t.m.ni asosiy xarakteristikasi zichlik funksiya hisoblanadi.
- Uzluksiz t.m. zichlik funksiyasi deb, shu t.m. taqsimot funksiyasidan olingan birinchi tartibli hosilaga aytiladi.
Uzluksiz t.m. zichlik funksiyasi f ( x ) orqali belgilanadi. Demak,
f ( x ) F ' ( x ) . (2.4.1)
Zichlik funksiyasi quyidagi xossalarga ega:
![f ( x ) funksiya manfiy emas, ya‘ni f ( x ) 0 . X uzluksiz t.m.ning [ a,b ] oraliqqa tegishli qiymatni qabul qilishi ehtimolligi zichlik funksiyaning a dan b gacha olingan aniq integralga teng, ya‘ni b P { a X b } f ( x ) d x . a Uzluksiz t.m. taqsimot funksiyasi zichlik funksiya orqali quyidagicha ifodalanadi: x F ( x ) f ( t ) dt . (2.4.2) gacha olingan xosmas integral 4 . Z ichlik fun k s iya si da n d a n birga tengdir f ( x ) d x 1 . I s b o t lar: 1 . F ( x ) k a m a ym ay di g a n f u nk s iya b o ‗ l g a ni u c h u n F ' ( x ) 0 , ya ‘ n i f ( x ) 0 . 2. tenglikdan Nyuton-Leybnis formulasiga P { a X b } F ( b ) F ( a ) a s o s a n: b b F ( b ) F ( a ) F ' ( x ) d x f ( x ) d x . a a b P { a X b } f ( x ) d x . Bu yerdan a 2-xossadan foydalanamiz: x F ( x ) P { X x } P { X x } f ( t ) d t . Agar 2-xossada a va b deb olsak, u holda muqarrar X ( , ) ga h o d i saga e ga b o ‗ la m i z , u h o l d a f ( x ) d x P { X } P { } 1 . ■ a 2.3.- m i sol. X t . m . z ich l ik fun k s iy a s i berilgan. O‗zgarmas a parametrni toping. ten g l i k b il a n f ( x ) 1 x 2](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img43.jpg)
- f ( x ) funksiya manfiy emas, ya‘ni
f ( x ) 0 .
- X uzluksiz t.m.ning [ a,b ] oraliqqa tegishli qiymatni qabul qilishi ehtimolligi zichlik funksiyaning a dan b gacha olingan aniq integralga teng, ya‘ni
b
P { a X b } f ( x ) d x .
a
- Uzluksiz t.m. taqsimot funksiyasi zichlik funksiya orqali quyidagicha ifodalanadi:
x
F ( x ) f ( t ) dt .
(2.4.2)
gacha olingan xosmas integral
4 . Z ichlik fun k s iya si da n d a n birga tengdir
f ( x ) d x 1 .
I s b o t lar: 1 . F ( x ) k a m a ym ay di g a n f u nk s iya b o ‗ l g a ni u c h u n F ' ( x ) 0 , ya ‘ n i
f ( x ) 0 .
2. tenglikdan Nyuton-Leybnis formulasiga
P { a X b } F ( b ) F ( a )
a s o s a n:
b b
F ( b ) F ( a ) F ' ( x ) d x f ( x ) d x .
a a
b
P { a X b } f ( x ) d x .
Bu yerdan
a
- 2-xossadan foydalanamiz:
x
F ( x ) P { X x } P { X x } f ( t ) d t .
- Agar 2-xossada a va b deb olsak, u holda muqarrar
X ( , ) ga h o d i saga e ga b o ‗ la m i z , u h o l d a
f ( x ) d x P { X } P { } 1 .
■
a
2.3.- m i sol. X t . m . z ich l ik fun k s iy a s i berilgan. O‗zgarmas a parametrni toping.
ten g l i k b il a n
f ( x )
1 x 2

a
1 x 2 d x 1 ,
Zichlik
4-xossasiga
k o ‗ ra
ya ‘ n i
funksiyaning
2
d
1
a l im
a 1 .
d
d x a l im ar c tg x | a
Dem a k,
c
1 x 2
2
d
d c
c c
a 1 .
2.5 Tasodifiy miqdorning sonli xarakteristikalari
X diskret t.m. taqsimot qonuni berilgan
{ p i P { X x i }, i 1 , 2 , . . ., n , . . . }.
b o ‗ l s i n :
Matematik kutilma
- X t . m . mat e mat ik k uti lma s i d e b, x i p i
i 1
qator yig‗indisiga aytiladi va
MX x i p i
i 1
( 2 .5.1)
orqali belgilanadi.
Matematik kutilmaning ma‘nosi shuki, u t.m. o‗rta qiymatini
ifodalaydi. Haqiqatan ham p i 1 ekanligini hisobga olsak, u holda
i 1
x i p i
i 1
i i
MX x p
x
.
o ' rta c ha
p
i 1
i
i 1
- Uzluksiz t.m. matematik kutilmasi deb
M X x f ( x ) d x
( 2 .5.2)
ya‘ni
integralga aytiladi. (2.5.2) integral absolut yaqinlashuvchi,
x f ( x ) dx
bo‗lsa matematik kutilma chekli, aks holda matematik
kutilma mavjud emas deyiladi.

Matematik kutilmaning xossalari:
- O‗zgarmas sonning matematik kutilmasi shu sonning o‗ziga teng, ya‘ni
MC = C.
- O‗zgarmas ko‗paytuvchini matematik kutilish belgisidan tashqariga chiqarish mumkin,
M ( CX )= CMX.
- Yig‗indining matematik kutilmasi matematik kutilmalar yig‗indisiga teng,
M ( X+Y )= MX+MY.
- Agar X Y bo‗lsa,
M ( X Y )= MX MY.
Isbotlar: 1. O‗zgarmas C sonni faqat 1 ta qiymatni bir ehtimollik bilan qabul qiluvchi t.m. sifatida qarash mumkin. Shuning uchun MC = C P { X = C }= C 1= C.
- C X diskret t.m. C x i ( i 1, n ) qiymatlarni p i ehtimolliklar bilan qabul
n n
qil s i n , u h o l da M C X C x i p i C x i p i C M X .
i 1 i 1
- X+Y diskret t.m. x i y i qiymatlarni p ij P { X x i , Y y j } ehtimolliklar bilan qabul qiladi, u holda ixtiyoriy n va m lar uchun
n m n m n m
M ( X Y ) ( x i y j ) p ij x i p ij y j p ij
i 1 j 1 i 1 j 1 i 1 j 1
n m m n n m
x i p ij y i p ij x i p i y j p j MX MY
i 1 j 1 j 1 i 1 i 1 j 1
m n
p ij p i p ij p j
B u ye r d a
va bo‗ladi.
C h u n k i,
j 1 i 1
m
m
{ X x i ; Y y j } { X x i } { Y y j } { X x i }
j 1
{ X x i } ,
j 1
m
m m
p i P { X x i } P { X x i ; Y y j } P { X x i ; Y y j } p ij .
j 1
4. Agar X Y bo‗lsa, u holda
j 1 j 1
p ij P { X x i , Y y j } P { X x i } P { Y y j } p i p j
va

M X Y x i y i P { X x i , Y y j }
i 1 j 1
p ij
n m
n m n m
x i y i P { X x i } P { Y y j } x i p i y i p j MX MY .
i 1 j 1 i 1
j 1
p
p
i
j
■ Matematik kutilmaning xossalari t.m. uzluksiz bo‗lganda ham hiddi s h u nga o‗ x s h a s h i s b otl a n a di. M a s a lan,
MCX C x f ( x ) dx C x f ( x ) dx C MX .
2.4.-misol. X diskret t.m. taqsimot qonuni berilgan bo‗lsa, X t.m.ning matematik kutilmasini toping.
X
P
500
50
0.01
10
0.05
1
0.1
0.15
0
0.69
MX =500 0.01+50 0.05+10 0.1+1 0.15+0 0.69=8.65.
2.5.-misol. X uzluksiz t.m. zichlik funksiyasi berilgan
0 , x ( 0 , 1 )
f ( x )
.
2
C x , x ( 0 , 1 )
C va MX ni toping.
f ( x ) d x 1 .
Dem a k,
Z ichlik f u n k s iy a ning 4 - x o ss a s i ga k o ‗ ra
1
x 3
0 , x ( 0 , 1 )
1
C x 2 d x C | 1 C 1 ,
C 3 v a f ( x )
.
0
3 3
3 x 2 , x ( 0 , 1 )
0
Endi matematik kutilmani hisoblaymiz:
3
4
1
M X x f ( x ) d x 3 x x 2 d x
0
.
Dispersiya
- X t.m. dispersiyasi deb, M ( X MX ) 2 ifodaga aytiladi. Dispersiya DX orqali belgilanadi. Demak,
D X M ( X M X ) 2 .
( 2 .5.3)
Agar X dickret t.m. bo‗lsa,
2
DX ( x M X ) p
,
( 2 .5.4)
i i
i 1
Agar X uzluksiz t.m. bo‗lsa,
D X ( x M X ) 2 f ( x ) d x
( 2 .5.5)
T.m. dispersiyasini hisoblash uchun quyidagi formula qulaydir:
DX = MX 2 -( MX ) 2 (2.5.6)
Bu formula matematik kutilma xossalari asosida quyidagicha keltirib chiqariladi:
D X M ( X M X ) 2 M ( X 2 2 XM X ( M X ) 2 ) M X 2 M ( 2 XM X ) M ( M X ) 2
M X 2 2 MXM X ( M X ) 2 M X 2 ( M X ) 2
Dispersiyaning xossalari:
- O‗zgarmas sonning dispersiyasi nolga teng DC =0.
- O‗zgarmas ko‗paytuvchini kvadratga ko‗tarib, dispersiya belgisidan tashqariga chiqarish mumkin,
D ( CX )= C 2 DX .
- Agar X Y bo‗lsa,
D ( X+Y )= DX+DY.
I s b o t lar: 1. D C M ( C M C ) 2 M ( C C ) 2 M 0 0 .
2. D ( CX ) M ( CX M ( CX )) 2 M ( CX CMX ) 2 M ( C 2 ( X MX ) 2 )
C 2 M ( X M X ) 2 C 2 D X .
- (2.5.6.) formulaga ko‗ra
D ( X Y ) M ( X Y ) 2 ( M ( X Y )) 2 MX 2 2 MXY MY 2 ( MX ) 2 2 MXMY ( MY ) 2
MX 2 ( MX ) 2 MY 2 ( MY ) 2 2( MXY MXMY ) DX DY 2( MXMY MXMY ) DX DY
■
2.6.-misol. X diskret t.m. taqsimot qonuni berilgan:
MX va DX ni hisoblaymiz:
MX =-1 0.2+0 0.1+1 0.3+2 0.4=0.9,
DX ( 1) 2 0.2 1 2 0.3 2 2 0.4 (0.9) 2 1.29 .
- X t.m. o‘rtacha kvadratik tarqoqligi ( chetlashishi ) deb, dispersiyadan olingan kvadrat ildizga aytiladi:
- X t.m. o‘rtacha kvadratik tarqoqligi ( chetlashishi ) deb, dispersiyadan olingan kvadrat ildizga aytiladi:
X
-1
P
0
0.2
0.1
1
0.3
2
0.4

X DX (2.5.7)
xossalaridan o‗rtacha kvadratik tarqoqlikning
Dispersiyaning
xo s s a lari k e lib c h iqa di: 1. C 0 ; 2. C X C X ;
2.6 Ba’zi muhim taqsimotlar Binomial taqsimot
- X diskret t.m. binomial qonun bo‗yicha taqsimlangan deyiladi, agar u 0,1,2,…n qiymatlarni
m m n m
p P { X m } C p q
, ( 2 . 6 .1)
m n
ehtimollik bilan qabul qilsa.
B u ye r d a 0 p 1 , q 1 p , m 0 , 1 , ... , n .
Binomial qonun bo‗yicha taqsimlangan X diskret t.m. yaqsimot qonuni quyidagi ko‗rinishga ega:
X=m
p m P { X m }
0
1
q n
2
C 1 p 1 q n 1
…
C 2 p 2 q n 2
n
…
m
n
…
C m p m q n m
n
…
n
p n
n
Nyuton binomiga asosan p m
m 0
orqali belgilaymiz.
( p q ) n 1 . B und a y ta q s i m ot n i B i ( n , p )
Uning taqsimot funksiyasi quyidagicha bo‗ladi:
0, agar x 0
m m n m
F ( x )
C p q , agar 0 x n
n
m x
1 , agar n x .
Endi bu taqsimotning sonli xarakteristikalarini hisoblaymiz.
n n
n
n
n 1
n
m m n m
m 1 m 1 n m
MX m P { X m } m P { X m } m C p q n p C p q
m 0
m 1
m 1
m 1
n p ( p q ) n 1 n p .

n
n
n
|
2
D X m P { X m } ( n p ) m C p q ( n p ) m m ( m 1 ) m
2 2
2 m m n m 2
m 1
m 0
n
n
n 2
C m 1 p m 1 q n m ( n p ) 2
m 2 m 2 n m
2
almashtirish bajaramiz| =
n 1 m 1
n ( n 1 ) p C p q
np
m 2
n ( n 1 ) p 2 n p ( n p ) 2 np q .
De m a k, M X np ; D X np q .
Puasson taqsimoti
- Agar X t.m. 0,1,2,…m,… qiymatlarni
a m e a
p m P { X m }
( 2 . 6 .2)
m !
ehtimolliklar bilan qabul qilsa, u Puasson qonuni bo‗yicha taqsimlangan
t.m. deyiladi. Bu yerda a biror musbat son.
Puasson qonuni bo‗yicha taqsimlangan X diskret t.m.ning taqsimot qonuni quyidagi ko‗rinishga ega:
X=m
p m P { X m }
0
1
e a
a e a
2
a 2 e a
…
1!
…
m
2!
…
a m e a
…
m !
a m
m !
a
p m e
a a
e e
Teylor yoyilmasiga asosan,
1 . B u taq s i m ot n i
m 0 m 0
( a ) orqali belgilaymiz. Uning taqsimot funksiyasi quyidagicha bo‗ladi:
0, agar m 0
a m e a
F ( x )
, agar 0 m x
m !
m x
Endi bu taqsimotning sonli xarakteristikalarini hisoblaymiz:
a m e a a m a m 1
MX m
m 0
a
a
m 1
m 1
a a
a e e a ,
e
m a e m !
( m 1 ) !
m !

a m 1 e a
a m e a
DX m
2
2
2
- a a m
- a
m !
( m 1 ) !
m 0
m 1
k a
k a
k a e
a e
a
a 2 a ( a 1 ) a 2 a
k !
k !
k 0
k 0
Demak, MX a ;
D X a .
Geometrik taqsimot
- Agar X t.m. 1,2,…m,… qiymatlarni
m 1
p m P { X m } q p
( 2 . 6 .3)
ehtimolliklar bilan qabul qilsa, u geometrik qonuni bo‗yicha taqsimlangan
t. m . de y il a di. B u y er d a p 1 q ( 0 , 1 ) .
Geometrik qonun bo‗yicha taqsimlangan t.m.larga misol sifatida quyidagilarni olish mumkin: sifatsiz mahsulot chiqqunga qadar tekshirilgan mahsulotlar soni; gerb tomoni tushgunga qadar tashlangan tangalar soni; nishonga tekkunga qadar otilgan o‗qlar soni va hokazo.
Geometrik qonun bo‗yicha taqsimlangan X diskret t.m. taqsimot
qonuni quyidagi ko‗rinishga ega:
X=m
p m P { X m }
1
p
2
qp
…
m
…
…
q m p
…
1
q p p q p
m 1
m 1
m 1
m 1
p 1
,
1 q p
chunki p m ehtimolliklar
g e o m e t r ik prog res s iy a ni ta s hk i l e tad i :
p , q p , q 2 p , q 3 p , .. . . S h un i ng u ch un h a m ( 2 . 6 .3) ta q s i m ot taq s i m ot d ey il a di va G e ( p ) or q a li bel g il a n a di.
Uning taqsimot funksiyasi quyidagicha bo‗ladi:
g e o m e t r ik
0 , aga r m 1
F ( x ) q m 1 p , aga r 1 m x
m x
![Endi bu taqsimotning sonli xarakteristikalarini hisoblaymiz: ' ' 1 M X m q m 1 p p m q m 1 p q m p 1 q q m 0 q m 1 m 1 1 p 1 , p p 2 (1 q ) 2 p DX m 2 q m 1 p 1 ( m 2 m ( m 1) m almashtirishni bajaramiz) p 2 m 1 m ( m 1) q m 1 p m q m 1 p 1 pq m ( m 1) q m 2 1 1 p 2 p 2 p m 1 m 1 m 1 '' 1 1 2 pq 1 1 q p 2 1 1 2 q q m pq . p p 2 p 3 p 2 p 2 p (1 q ) 3 p m 0 2 q DX q . Demak, MX 1 ; p 2 p Tekis taqsimot Agar uzluksiz X t.m. zichlik funksiyasi 1 , a g ar x [ a , b ] , f ( x ) b a ( 2 . 6 .4) 0, a g ar x [ a , b ] ko‗rinishda berilgan bo‗lsa, u [a,b] oraliqda tekis taqsimlangan t.m. deyiladi. Bu t.m.ning grafigi 14-rasmda berilgan. [ a , b ] oraliqda tekis taqsimlangan X t.m. ni X R [ a , b ] ko‗rinishda belgilanadi. X R [ a , b ] uchun taqsimot funksiyasini topamiz. (2.4.2) formulaga ko‗ra agar a x b bo‗lsa x x dt t x a F ( x ) b a b a b a , a a a g a r x a b o ‗ l s a , F ( x ) 0 va x b b o ‗ l s a , b a b x d t t F ( x ) 0 d t b a 0 d t b a 1 b o ‗ la d i. De m a k , a a b](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img51.jpg)
Endi bu taqsimotning sonli xarakteristikalarini hisoblaymiz:
' '
1
M X m q m 1 p p m q m 1 p q m p
1 q q
m 0 q
m 1 m 1
1 p 1 ,
p
p 2
(1 q ) 2 p
DX m 2 q m 1 p 1 ( m 2 m ( m 1) m almashtirishni bajaramiz)
p 2
m 1
m ( m 1) q m 1 p m q m 1 p 1 pq m ( m 1) q m 2 1 1
p 2 p 2
p
m 1
m 1 m 1
''
1 1 2 pq 1 1 q
p 2
1 1 2
q q m pq
.
p
p 2 p 3
p 2
p 2
p
(1 q ) 3 p
m 0
2
q
DX q .
Demak, MX 1 ;
p 2
p
Tekis taqsimot
- Agar uzluksiz X t.m. zichlik funksiyasi
1
, a g ar x [ a , b ] ,
f ( x ) b a
( 2 . 6 .4)
0, a g ar x [ a , b ]
ko‗rinishda berilgan bo‗lsa, u [a,b] oraliqda tekis taqsimlangan t.m. deyiladi.
Bu t.m.ning grafigi 14-rasmda berilgan. [ a , b ] oraliqda tekis taqsimlangan
X t.m. ni X R [ a , b ] ko‗rinishda belgilanadi. X R [ a , b ] uchun taqsimot funksiyasini topamiz. (2.4.2) formulaga ko‗ra agar a x b bo‗lsa
x
x
dt t
x a
F ( x ) b a b a b a ,
a
a
a g a r x a b o ‗ l s a , F ( x ) 0 va x b b o ‗ l s a ,
b
a b
x
d t t
F ( x ) 0 d t b a 0 d t b a
1 b o ‗ la d i. De m a k ,
a
a b
![ 0, agar x a bo'lsa, x a F ( x ) b a , a g a r a x b bo ' l s a , 1, agar b x bo'lsa, F ( x ) taqsimot funksiyaning grafigi 15-rasmda keltirilgan. 14 -rasm. 15 - ras m . X R [ a , b ] t.m. uchun MX va DX larni hisoblaymiz:](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img52.jpg)
0, agar x a bo'lsa,
x a
F ( x ) b a , a g a r a x b bo ' l s a ,
1, agar b x bo'lsa,
F ( x ) taqsimot funksiyaning grafigi 15-rasmda keltirilgan.
14 -rasm.
15 - ras m .
X
R [ a , b ] t.m. uchun MX va DX larni hisoblaymiz:
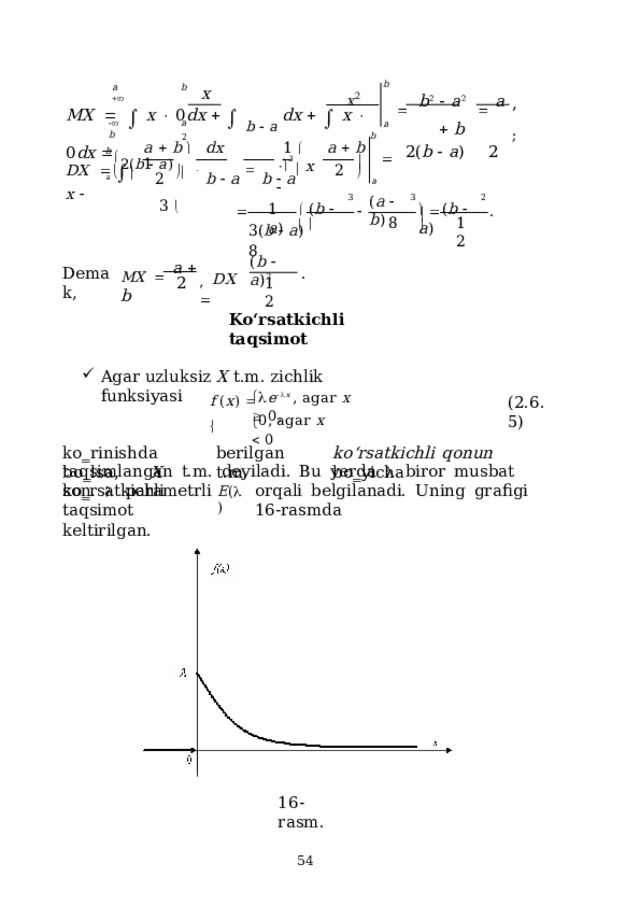
x 2
b
b 2 a 2 a b
2( b a ) 2
a b
x
M X x 0 d x b a d x x 0 d x 2 ( b a )
, ;
a b
a
b
b
1 a b 3
2
a b d x 1
D X x
x
2 b a b a 3
2
a
a
3
2
3
( b a )
( a b )
1 ( b a )
.
3( b a ) 8
1 2
8
M X a b
( b a ) 2
, DX
De m a k,
.
2
12
Ko‘rsatkichli taqsimot
- Agar uzluksiz X t.m. zichlik funksiyasi
e x , a g a r x 0 ,
f ( x )
( 2 . 6 .5)
0, agar x 0
k o ‗ r i n ish d a b e r i l g a n b o ‗ l s a , X t . m .
k o ‘ rs atki c h l i qon u n b o ‗ y icha
taqsimlangan t.m. deyiladi. Bu yerda biror musbat son. parametrli
orqali belgilanadi. Uning grafigi 16-rasmda
ko‗rsatkichli taqsimot keltirilgan.
E ( )
16 - ras m .
![17-rasm. Taqsimot funksiyasi quyidagicha ko‗rinishga ega bo‗ladi: 1 e x , a g a r x 0 , F ( x ) 0, agar x 0. Uning grafigi 17-rasmda keltirilgan. E ndi k o ‗ r s at k ich l i taq s i m ot n ing m a t e m a tik k u til m a s i va dispersiyasini hisoblaymiz: b b MX x e dx x x x lim x e dx lim xde b b 0 0 0 b 1 b b 1 e x x l i m x e x e dx lim , b 0 b 0 0 1 DX x 2 f ( x ) dx ( MX ) 2 x 2 e x dx 2 0 [bo'laklab integrallash formulasini ikki marta qo'llaymiz] ](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img54.jpg)
17-rasm.
Taqsimot funksiyasi quyidagicha ko‗rinishga ega bo‗ladi:
1 e x , a g a r x 0 ,
F ( x )
0, agar x 0.
Uning grafigi 17-rasmda keltirilgan.
E ndi k o ‗ r s at k ich l i taq s i m ot n ing m a t e m a tik k u til m a s i va dispersiyasini hisoblaymiz:
b
b
MX x e dx
x
x
x
lim x e dx lim xde
b
b
0
0
0
b
1
b
b
1
e x
x
l i m x e x
- e dx lim
,
b
0
b
0
0
1
DX x 2 f ( x ) dx ( MX ) 2 x 2 e x dx
2
0
[bo'laklab integrallash formulasini ikki marta qo'llaymiz]

x 2
b
1
2 x
1 2 1 1
e x
e x e x
l i m
.
2
2 2 2 2
b
0
E ( ) bo‗lsa, u holda MX 1 va DX 1 .
Demak, agar X
2
Normal taqsimot
Normal taqsimot ehtimollar nazariyasida o‗ziga xos o‗rin tutadi. Normal taqsimotning xususiyati shundan iboratki, u limit taqsimot hisoblanadi. Ya‘ni boshqa taqsimotlar ma‘lum shartlar ostida bu taqsimotga intiladi. Normal taqsimot amaliyotda eng ko‗p qo‗llaniladigan taqsimotdir.
- X uzluksiz t.m. normal qonun bo‗yicha taqsimlangan deyiladi, agar uning zichlik funksiyasi quyidagicha ko‗rinishga ega bo‗lsa
( x a ) 2
1
, x R
e
f ( x )
2 2
( 2 . 6 .6)
2
a va
p a ra m e t r lar b o ‗ y icha n or m a l taq s i m ot N ( a , ) o rqa li
0
b e l g il a n ad i. X N ( a , ) nor m a l t.m . ni n g t a q s i m ot fun k s iy a s i
x ( t a ) 2
1
e 2 2 d t .
F ( x )
( 2 . 6 . 7 )
2
Agar normal taqsimot parametrlari a =0 va 1 bo‗lsa, u standart normal taqsimot deyiladi. Standart normal taqsimotning zichlik funksiyasi quyidagicha ko‗rinishga ega:
- x 2
2 .
1
( x )
e
2
Bu funksiya bilan 1.14 paragrafda tanishgan edik(uning grafigi 9- rasmda keltirilgan). Taqsimot funksiyasi
x
1
e 2 dt
t 2
( x )
2

ko‗rinishga ega va u Laplas funksiyasi deyiladi(uning grafigi 10-rasmda keltirilgan).
a va p a r a m e t r lar n i m a ‘ n osini a niql a y m iz. B uni n g u c h u n
X N ( a , ) t.m.ning matematik kutilmasi va dispersiyasini hisoblaymiz:
M X x f ( x ) d x
( x a ) 2
1
x a
x e 2 2 dx
=t almashtirish bajaramiz
2
2
1 (
a
a
e t 2 d t 0
2
2
2 dt
a
2 t a ) e t 2
t
t e d t
2
B i r i n c hi int e gral no l ga ten g , c h u n k i int e gral o s t i d a gi fun k s iya toq,
integrallash chegarasi esa nolga nisbatan simmetrikdir. Ikkinchi integral esa Puasson integrali deyiladi,
e t 2 d t .
Shunday qilib, a parametr matematik kutilmani bildirar ekan. Dispersiya
hiso b la s hda x a =t a lm a s hti r i sh va b o ‗ lakl a b i nte g rallas h d a n foydalanamiz:
2
( x a ) 2
D X ( x a ) 2 f ( x ) d x
1
( x a ) 2 e dx
2 2
2
2
2
2
2
1
1
1 2 2 t 2 e t 2
2
2
2
2 t
t
t
- te
t e dt
e d t
2 dt
2
2
2
2 2 1
2
.
2
Demak, DX 2 va o‗rtacha kvadratik tarqoqlikni bildirar ekan.
18 - ras m da a va lar n ing t ur l i qi y m a tl a r i da nor m a l taq s i m ot grafigining o‗zgarishi tasvirlangan:
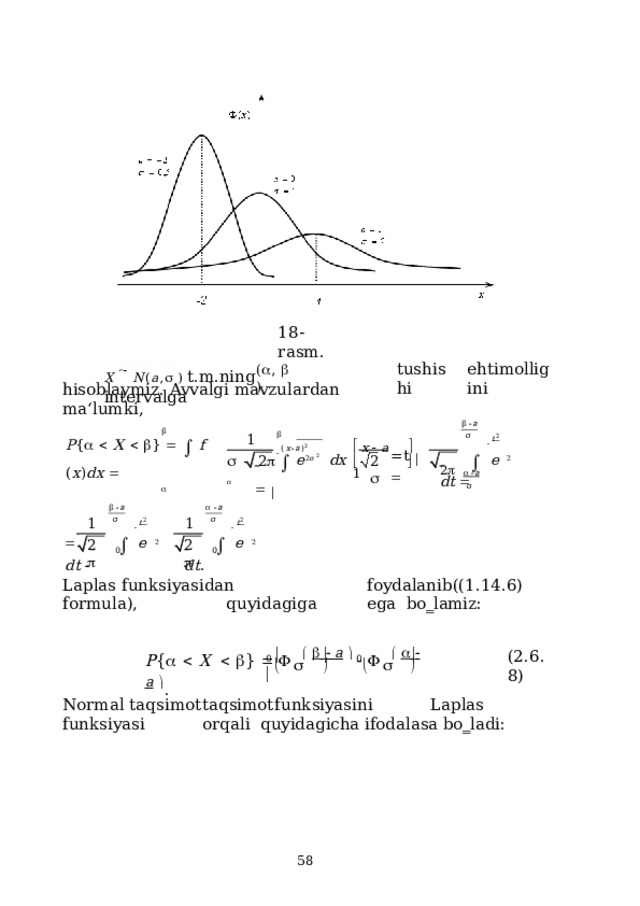
18 - ras m .
X N ( a , ) t.m.ning intervalga
tushishi
ehtimolligini
( , )
hisoblaymiz. Avvalgi mavzulardan ma‘lumki,
a
t 2
( x a ) 2
P { X } f ( x ) d x
1
x a 1
e 2 2 dx
e 2 dt
=t
2
2
2 a
a
a
t 2
t 2
1
1
e 2 dt .
e 2 dt
2
2
0
0
L a p las funk s iy a s i d a n f o y d a lani b ((1.14. 6 ) f or m ula), qu y i d ag i g a e ga bo‗lamiz:
P { X } a a .
( 2 . 6 . 8 )
0 0
No r m a l taq s i m ot taq s i m ot f u n k s iya s i n i L a p las funk s iy a s i or q a li quyidagicha ifodalasa bo‗ladi:
( t a ) 2
x
a
x a
1
F ( x )
e 2 2 dt P { X x }
0
0
2
x a x a 1
0
( 2 . 6 . 9 )
0
0
2
x
1
e 2 dt
t 2
( x )
b o ‗ l s a , u hol d a
Agar Laplas funksiyasi
2
F ( x ) x a va (2.6.8) formulani quyidagicha yozsa bo‗ladi:
P { X } a a .
(2.6.10)
Amaliyotda ko‗p hollarda normal t.m.ning a ga nisbatan simmetrik bo‗lgan intervalga tushishi ehtimolligini hisoblashga to‗gri keladi. Uzunligi 2 l
b o ‗ l g a n i n te r v a l n i ola y lik, u h o l d a
( a - l , a l )
P { a l X a l } P { X a l }
a l a a l a 2 l 2 l 1.
0 0 0
Dem a k,
P { X a l } 2 l 2 l 1.
0
( 2 . 6 . 11 )
P { X a 3 } 2 0 3
0 x
( 2 . 6 . 1 1 ) da l 3 d e b o l s a k, b o‗ l ad i.
funksiyaning qiymatlari jadvalidan 0 3 0.49865 ni topamiz. U holda
P { X a 3 } 0 . 997 3
bo‗ladi. Bundan quyidagi muhim natijaga ega
N ( a , ) b o ‗ l s a , u h ol d a u n i ng m a t e m a tik k u til i s h i d a n
bo‗lamiz: Agar c h e tl a s hishini n g a b s o l u t
X
qiymati o‗rtacha kvadratik tarqoqligining
uchlanganidan katta bo‗lmaydi. Bu qoida ― uch sigma qoidasi ‖ deyiladi(19- rasm).
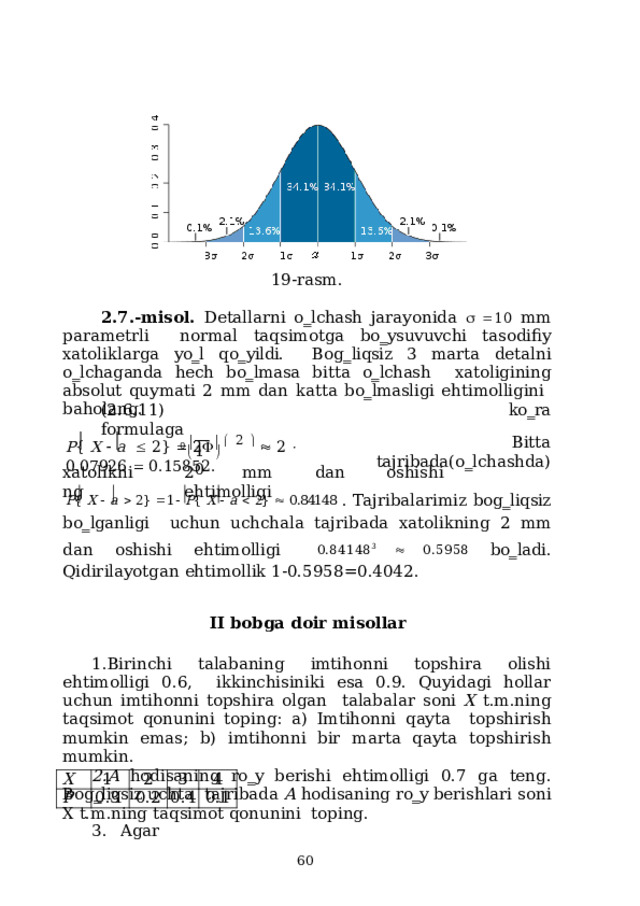
19-rasm.
2.7.-misol. Detallarni o‗lchash jarayonida 10 mm parametrli normal taqsimotga bo‗ysuvuvchi tasodifiy xatoliklarga yo‗l qo‗yildi. Bog‗liqsiz 3 marta detalni o‗lchaganda hech bo‗lmasa bitta o‗lchash xatoligining absolut quymati 2 mm dan katta bo‗lmasligi ehtimolligini baholang.
ko‗ra
(2.6.11) formulaga
Bitta tajribada(o‗lchashda)
P { X a 2 } 2 2 2 0 . 0 792 6 0 . 1 5852 .
0
10
2 mm dan oshishi ehtimolligi
xatolikning
P { X a 2} 1 P { X a 2} 0.84148 . Tajribalarimiz bog‗liqsiz bo‗lganligi uchun uchchala tajribada xatolikning 2 mm dan oshishi ehtimolligi 0.84148 3 0.5958 bo‗ladi. Qidirilayotgan ehtimollik 1-0.5958=0.4042.
II bobga doir misollar
- Birinchi talabaning imtihonni topshira olishi ehtimolligi 0.6, ikkinchisiniki esa 0.9. Quyidagi hollar uchun imtihonni topshira olgan talabalar soni X t.m.ning taqsimot qonunini toping: a) Imtihonni qayta topshirish mumkin emas; b) imtihonni bir marta qayta topshirish mumkin.
- A hodisaning ro‗y berishi ehtimolligi 0.7 ga teng. Bog‗liqsiz uchta tajribada A hodisaning ro‗y berishlari soni X t.m.ning taqsimot qonunini toping.
- Agar
X
1
P
2
0.3
0.2
3
4
0.4
0.1

bo‗lsa, X t.m.ning taqsimot funksiyasini toping.
- Ikki ovchi bir nishonga qarata o‗q uzishmoqda. Birinchi ovchining nishonga tekkazishi ehtimolligi 0.6, ikkinchisiniki esa 0.8 bo‗lsa, nishonga tekkan o‗qlar soni X t.m.ning taqsimot qununini toping va taqsimot funksiyasini tuzing.
- Taqsimot funksiyasi
0, agar x 0,
0 . 2 , a g a r 0 x 1 ,
F ( x )
0 . 6 , a g a r 1 x 2 ,
1, agar x 2
bo‗lgan X t.m.ning qabul qilishi mumkin bo‗lgan qiymatlari va ularga mos ehtimolliklarini toping.
- Agar P { X 3 } 1 b o ‗ l s a , F ( 3 ) ni hiso b la n g.
- Quyidagi
X
3
fun k s iy a lar d a n q ay s il a ri z ichlik f u n k s iya b o ‗ lad i :
1
f ( x ) x 2 , f ( x ) 1 s i n x 1 , f ( x ) 1
.
1 2
3
2 2 1 x 2
8. Tasodifiy miqdorning zichlik funksiyasi
x h ,
3 x 2 ,
x h ,
f ( x ) 2
0,
bo‗lsa h ning qiymatini toping.
9. Taqsimot funksiyasi
0, agar x 0,
x 2
F ( x ) , agar, 0 x
2 ,
2
1, agar x 2,
b o ‗ l g a n X t. m .ning z ichlik f u n k s i y a s i n i top i ng va ehtimollikni hisoblang.
10. Agar X t.m.ning taqsimot funksiyasi
P { x X 1 }

0, agar x 1,
2
F ( x ) a ( x 1 ) , aga r , - 1 x 2 ,
1, agar x 2
bo‗lsa, o‗zgarmas a ning qiymatini hisoblang.
11. Tasodifiy miqdorning zichlik funksiyasi
,
0, agar x
2
f ( x ) a cos x , agar x ,
2
2
0 agar x ,
2
bo‗lsa, o‗zgarmas a ning qiymatini va t.m.ning taqsimot funksiyasini hisoblang.
12. Uzluksiz X t.m. zichlik funksiyasining grafigi berilgan:
20 - ras m .
zichlik funksiya f ( x ) ning ifodasini,
taq si m ot f u n k s i y a s i n i va
F ( x )
1 X 1 ho d i s a n i ng e hti m o l lig i ni h i s o bla n g.
4
13. X R (0, a ) va P X 1 1 bo‗lsa, a ning qiymatini toping.
3
3
14. Uzluksiz X t.m.ning zichlik funksiyasi:
![ 0 , a g a r x 0 v a x , f ( x ) 1 s in x , a g a r 0 x , 2 bo‗lsa, MX va DX ni hisoblang. X va Y bog‗liqsiz diskret t.m.lar bo‗lib, MX =0, MY =-3, DX =2, DY =9 bo‗lsa, Z =5 X -3 Y +2 t.m. uchun MZ va DZ ni hisoblang. Uzluksiz X t.m.ning taqsimot qonuni: 0, agar x A , 2 F ( x ) 0.25 x , agar A x B , 1, agar x B , bo‗lsa, A va B qiymatlarini toping, MX va X ni hisoblang. P { 3 X 5 } , P { X 4 } , P { X 3 6 } 17 . X N ( 3 , 2 ) b o ‗ l s a , ehtimolliklarni hisoblang. Agar X B i ( 1 ; 0 . 5 ) b o ‗ l s a , ( M X ) 2 va DX ni taq q o s la n g. Quyida X t.m.ning taqsimot jadvali berilgan: X P -0.5 0 0.1 0.5 0.4 0.1 1 0.3 1.5 0.1 a) Y = 1 0 X - 1; Z =- X 2 b) V=2 X t.m.larning matematik kutilmasi va dispersiyaslarini c) hiso b la n g. Agar X (23) va Y =1- X bo‗lsa F Y (2) ni hisoblang. Uzluksiz X t.m.ning zichlik funksiyasi quyidagicha ko‗rinishga ega: 3 h , x [ 1 , 0 ] , f ( x ) h , x [ 0 , 2 ] , 0, aks holda. h ni, X t.m.ning taqsimot funksiyasi F ( x ) ni, M [(2- X )( X -3)] va D [2- 3 X ] ni hisoblang. 22. X t.m.ning taqsimot funksiyasi 1 1 , a g a r x 1 , F ( x ) x 0, a g a r x 1 ,](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img62.jpg)
0 , a g a r x 0 v a x ,
f ( x )
1 s in x , a g a r 0 x ,
2
bo‗lsa, MX va DX ni hisoblang.
- X va Y bog‗liqsiz diskret t.m.lar bo‗lib, MX =0, MY =-3, DX =2, DY =9 bo‗lsa, Z =5 X -3 Y +2 t.m. uchun MZ va DZ ni hisoblang.
- Uzluksiz X t.m.ning taqsimot qonuni:
0, agar x A ,
2
F ( x ) 0.25 x , agar A x B ,
1, agar x B ,
bo‗lsa, A va B qiymatlarini toping, MX va X ni hisoblang.
P { 3 X 5 } , P { X 4 } , P { X 3 6 }
17 . X N ( 3 , 2 ) b o ‗ l s a ,
ehtimolliklarni hisoblang.
- Agar X B i ( 1 ; 0 . 5 ) b o ‗ l s a , ( M X ) 2 va DX ni taq q o s la n g.
- Quyida X t.m.ning taqsimot jadvali berilgan:
X
P
-0.5
0
0.1
0.5
0.4
0.1
1
0.3
1.5
0.1
a)
Y = 1 0 X - 1; Z =- X 2
b)
V=2 X t.m.larning matematik kutilmasi va dispersiyaslarini
c) hiso b la n g.
- Agar X (23) va Y =1- X bo‗lsa F Y (2) ni hisoblang.
- Uzluksiz X t.m.ning zichlik funksiyasi quyidagicha ko‗rinishga
ega:
3 h , x [ 1 , 0 ] ,
f ( x ) h , x [ 0 , 2 ] ,
0, aks holda.
h ni, X t.m.ning taqsimot funksiyasi F ( x ) ni, M [(2- X )( X -3)] va D [2- 3 X ] ni hisoblang.
22. X t.m.ning taqsimot funksiyasi
1 1 , a g a r x 1 ,
F ( x )
x
0, a g a r x 1 ,
![bo‗lsa, P { X a } 1 tenglik o‗rinli bo‗ladigan a ning qiymatini toping. 3 23. X uzluksiz t.m.ning taqsimot funksiyasi F ( x ) c b arc t g x a formula orqali aniqlanadi. Quyidagilarni toping: a) o‗zgarmas a , b va c larning qiymatlari; b) X t.m.ning zichlik funksiyasi. 24. X t.m.ning taqsimot funksiyasi 1 e 2 x , x 0 , F ( x ) 0, x 0 k o ‗ r i n ish g a e ga b o ‗ l s a , M [ ( X 4 )( 5 X )] , P { X M X } va hisoblang. lar n i 25. Agar f ( x ) zichlik funksiyasi bo‗lsa, u holda zichlik funksiya bo‗ladimi? D ( 3 2 X ) f ( x ) funksiya](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img63.jpg)
bo‗lsa, P { X a } 1 tenglik o‗rinli bo‗ladigan a ning qiymatini toping.
3
23. X uzluksiz t.m.ning taqsimot funksiyasi
F ( x ) c b arc t g x
a
formula orqali aniqlanadi. Quyidagilarni toping: a) o‗zgarmas a , b va c
larning qiymatlari; b) X t.m.ning zichlik funksiyasi.
24. X t.m.ning taqsimot funksiyasi
1 e 2 x , x 0 ,
F ( x )
0, x 0
k o ‗ r i n ish g a e ga b o ‗ l s a , M [ ( X 4 )( 5 X )] , P { X M X } va hisoblang.
lar n i
25. Agar f ( x ) zichlik funksiyasi bo‗lsa, u holda
zichlik funksiya bo‗ladimi?
D ( 3 2 X )
f ( x ) funksiya
III bob. Ko‘p o‘lchovli tasodifiy miqdorlar
3.1 Ko‘p o‘lchovli tasodifiy miqdorlar va ularning birgalikdagi taqsimot funksiyasi
Bir o‗lchovli t.m.lardan tashqari, mumkin bo‗lgan qiymarlari 2 ta, 3 ta, ..., n ta son bilan aniqlanadigan miqdorlarni ham o‗rganish zarurati tug‗iladi. Bunday miqdorlar mos ravishda ikki o‗lchovli, uch o‗lchovli, … , n o‗lchovli deb ataladi.
Faraz qilaylik, ( , A, P ) ehtimollik fazosida aniqlangan X 1 , X 2 ,..., X n
t.m.lar berilgan bo‗lsin.
- vektorga tasodifiy vektor yoki n -o‗lchovli t.m.
X ( X 1 , X 2 , ..., X n )
deyiladi.
Ko‗p o‗lchovli t.m. har bir elementar hodisa ga n ta t.m.larning qabul qiladigan qiymatlarini mos qo‗yadi.
- F X , X ,..., X ( x 1 , x 2 ,..., x n ) P { X 1 x 1 , X 2 x 2 ,..., X n x n }
1 2 n
X 1 , X 2 , ... , X n
n o ‗ lc h ov l i
funksiya tasodifiy vektorning taqsimot funksiyasi yoki
X ( X 1 , X 2 , ..., X n )
X 1 , X 2 ,..., X n t.m.larning birgalikdagi taqsimot funksiyasi deyiladi.
f un k s iy a ni k o ‗ r i n i s h i d a
F X , X , . . ., X ( x 1 , x 2 , ..., x n )
1 2 n
Qulaylik
u ch un
taq s i m ot
X 1 , X 2 , ... , X n
yozamiz.
F ( x 1 , x 2 , ... , x n )
indekslarini tushirib qoldirib,
F ( x 1 , x 2 , ... , x n )
taqsimot funksiyasi bo‗lsin. Ko‗p o‗lchovli
v e k t o r n i ng taq s imot
funksiya
tas o d i f iy
X ( X 1 , X 2 , ..., X n )
F ( x 1 , x 2 , ... , x n )
funksiyaning asosiy xossalarini keltiramiz:
0 F ( x 1 , x 2 , . . ., x n ) 1 ,
1. ya‘ni taqsimot funksiya
x i :
chegaralangan.
- F ( x 1 , x 2 ,..., x n ) funksiya har qaysi argumenti bo‗yicha kamayuvchi emas va chapdan uzluksiz.
- Agar biror x i bo‗lsa, u holda
lim F ( x 1 , x 2 ,..., x n ) F ( x 1 ,..., x i 1 , , x i 1 ,..., x n )
x i
( 3 .1.1)
, ... , X ( x 1 , ... , x i 1 , x i 1 , . .. , x n )
F X , ... , X , X
1 i 1 i 1 n
l i m F ( x 1 , x 2 , ... , x n ) 0 .
4. Agar biror x i bo‗lsa, u holda
x i

3-xossa yordamida keltirib chiqarilgan (3.1.1) taqsimot funksiyaga marginal(xususiy) taqsimot funksiya deyiladi. X ( X 1 , X 2 ,..., X n ) tasodifiy vektorning barcha marginal taqsimot funksiyalari soni
n
n n n n
1 2 n 1
m 0 n n
ga tengdir.
k C C ... C C C C 2 2
n n
n 0
M a s a lan,
( n =2) ikki o‗lchovlik tasodifiy vektorning
X ( X 1 , X 2 )
m a r g i n a l ta q s i m ot fun k s iy a lari quyidagilardir:
s on i ta b o ‗ l i b, u lar
F ( , x 2 ) F 2 ( x 2 ) P ( X 2 x 2 ) .
k 2 2 2 2
F ( x 1 , ) F 1 ( x 1 ) P ( X 1 x 1 ) ;
Soddalik uchun n =2 bo‗lgan holda, ya‘ni ( X , Y ) ikki o‗lchovlik tasodifiy vector bo‗lgan holni ko‗rish bilan cheklanamiz.
3.2 Ikki o‘lchovli diskret tasodifiy miqdor va uning taqsimot qonuni
( X , Y ) ikki o‗lchovli t.m. taqsimot qonunini
p i j P { X x i , Y y j } ; i 1 , n , j 1 , m
( 3 .2.1)
formula yordamida yoki quyidagi jadval ko‗rinishida berish mumkin:
Y
x 1
y 1
X
x 2
p 11
y 2
p 12
p 21
…
…
p 22
x n
…
y m
…
p n 1
…
…
p 1 m
p 21
…
p 2 m
…
…
p nm
( 3 .2.2)
b u ye r d a b a rcha
e hti m olli k lar y i g ‗ ind i s i b i r g a ten g , c hun k i
p ij
{ X x i , Y y j } i 1, n , j 1, m birgalikda bo‗lmagan hodisalar to‗la gruppani
tashkil etadi p ij 1 . (3.2.1) formula ikki o‗lchovli diskret t.m.ning
i 1 j 1
taqsimot qonuni, (3.2.2) jadval esa birgalikdagi taqsimot jadvali deyiladi. ( X , Y ) ikki o‗lchovli diskret t.m.ning birgalikdagi taqsimot qonuni
n m
berilgan bo‗lsa, har bir komponentaning alohida (marginal) taqsimot
qo n u n larini to p i sh m u m ki n . H a r bir u c hun
i 1 , n
b i r g a li k da Dem a k,
hodisalar
{ X x i , Y y 1 } , { X x i , Y y 2 } , ... , { X x i , Y y m }
p x P { X x i } p i 1 p i 2 ... p im .
bo‗lmagani sababli:
i
m
n
i ij
p x P { X x i } p ,
j ij
i 1 , n , p y P { Y y j } p j 1 , m .
j 1 i 1
3.1-misol. Ichida 2 ta oq, 1 ta qora, 1 ta ko‗k shar bo‗lgan idishdan tavakkaliga ikkita shar olinadi. Olingan sharlar ichida qora sharlar soni X
t.m. va ko‗k rangdagi sharlar soni Y t.m. bo‗lsin. ( X , Y ) ikki o‗lchovli
t.m.ning birgalikdagi taqsimot qonunini tuzing. X va Y t.m.larning alohida taqsimot qonunlarini toping.
X t.m. qabul qilishi mumkin qiymatlari: 0 va 1: Y t.m.ning qiymatlari
Mos e hti m olli k la r ni hiso b la y m iz:
h a m 0 va 1.
(yoki
C 2
2 1 1
4 3 6
1
6
2
6
P { X 0, Y 0} 2
);
p 11
C 2
4
C 1
2
6
; p P { X 1 , Y 0 }
p 12 P { X 0, Y 1} 2
;
C 2
21
4
p P { X 1 , Y 1 } 1 .
22
6
( X , Y ) vaktorning taqsimot jadvali quyidagicha ko‗rinishga ega:
Y
0
0
X
1
1
2
1
6
2
6
6
1
6
P { X 0 } 1 2 1 , P { X 1 } 2 1 1 ;
6 6 2 6 6 2
B u ye r d a n
P { Y 0 } 1 2 1 , P { Y 1 } 2 1 1 k e lib c h i q a di. X
6 6 2 6 6 2
va Y t.m.larning alohida taqsimot qonunlari quyidagi ko‗rinishga ega bo‗ladi:
Y : 0 , 1
X : 0 , 1
1 .
2 2 2 2
1 va p : 1 ,
p : 1 ,
- Ikki o‘lchovli tasodifiy miqdorning taqsimot funksiyasi va uning xossalari
- Ikki o‘lchovli tasodifiy miqdorning taqsimot funksiyasi va uning xossalari
Ikki o‗lchovli t.m. taqsimot funksiyasini F ( x , y ) orqali belgilaymiz.
- Ikki o‘lcholi (X,Y) t.m.ning taqsimot funksiyasi , x va y sonlarning har bir jufti uchun { X x } va { Y y } hodisalarning birgalikdagi ehtimolligini
- Ikki o‘lcholi (X,Y) t.m.ning taqsimot funksiyasi , x va y sonlarning har bir jufti uchun { X x } va { Y y } hodisalarning birgalikdagi ehtimolligini
- Ikki o‘lcholi (X,Y) t.m.ning taqsimot funksiyasi , x va y sonlarning har bir jufti uchun { X x } va { Y y } hodisalarning birgalikdagi ehtimolligini
aniqlaydigan F ( x , y ) funksiyasidir: ya‘ni

( 3 .3.1)
F ( x , y ) P { X x , Y y } P ( X . Y ) ( , x ) ( , y ) D .
(3.3.1.) tenglikning geometrik tasviri 21-rasmda keltirilgan.
21-rasm.
( X , Y ) i kki o ‗ lcho v lik d i s kret t. m . t a q s i m ot f u n k s iy a s i qu yi d a gi yig‗indi orqali aniqlanadi:
( 3 .3.2)
F ( x , y )
p ij .
x i x y j y
Ikki o‗lchovlik t.m. taqsimot funksiyasining xossalari:
- F ( x , y ) taqsimot funksiya chegaralangan: 0 F ( x , y ) 1 .
- F ( x , y ) funksiya har qaysi argumenti bo‗yicha kamayuvchi emas: a g a r x 2 x 1 b o ‗ l s a , F ( x 2 , y ) F ( x 1 , y ) ,
a g a r y 2 y 1 b o ‗ l s a , F ( x , y 2 ) F ( x , y 1 ) .
- F ( x , y ) funksiyaning biror argumenti bo‗lsa(limit ma‘nosida), u holda F ( x , y ) funksiya nolga teng, F ( x , ) F ( , y ) F ( , ) 0 .
- Agar F ( x , y ) funk s iy a ni n g b i tta a rgum e nti b o ‗ l s a ( l i m it ma‘nosida), u holda
F ( x , ) F 1 ( x ) F X ( x ) ; F ( , y ) F 2 ( y ) F Y ( y ) . ( 3 .3.3)

4 ' . Agar ikkala argumenti bo‗lsa(limit ma‘nosida), u holda
F ( , ) 1 .
5. F ( x , y ) funksiya har qaysi argumenti bo‗yicha chapdan uzluksiz,
ya ‘ n i l i m F ( x , y ) F ( x 0 , y ) , l i m F ( x , y ) F ( x , y 0 ) .
x x 0 0 y y 0 0
Isboti. 1. F ( x , y ) P { X x , Y y } ehtimollik bo‗lgaligi uchun
0 F ( x , y ) 1 .
2. ( x , y ) argumentlarning birortasini kattalashtirsak, 21-rasmda bo‗yalgan D soha kattalashadi, demak bu sohaga ( X , Y ) tasodifiy nuqtaning tushishi ehtimolligi kamaymaydi.
3. h o d i s a lar v a ular n i ng k o ‗ p a y tm a s i m u m kin
{ X } , { Y }
bo‗lmagan hodisalardir. Demak, bu hodisalarning ehtimolligi nolga teng.
4. { X } muqarrar hodisa bo‗lgani uchun
{ X } { Y y } { Y y }
F ( , y ) P { X ; Y y } P { Y y } F Y ( y ) .
b o ‗ ladi. D e m a k, X uddi
shunday F ( x , ) P { X x ; Y } P { X x } F X ( x ) .
4 ' . { X } va { Y } hodisalar muqarrar hodisalar bo‗lganligi uchun
{ X } { Y } ham muqarrar hodisa bo‗ladi va bu hodisaning
ehtimolligi 1 ga teng. ■
F ( x , y ) taq s i m ot f u nk s iya y or d a m i d a ( X , Y ) t. m .
bi r or s oh a ga t u s h i s hi e hti m olli g i ni t op i s h
D { ( x , y ) : x 1 x x 2 , y 1 y y 2 }
mumkin:
P { ( X , Y ) D } P { x 1 X x 2 , y 1 Y y 2 }
F ( x 2 , y 2 ) F ( x 1 , y 2 ) F ( x 2 , y 1 ) F ( x 1 , y 1 ) .
22-rasmda (3.3.4) tenglikning geometrik isboti keltirilgan.
( 3 .3.4)
22 - ras m .

3.2-misol. 3.1-misoldagi ( X , Y ) ikki o‗lchovlik t.m.ning hamda X va Y
t.m.larning taqsimot funksiyalarini toping. Avvalgi bobdagi (2.3.2) formuladan:
0, agar x 0, 0, agar y 0,
F ( x ) 0. 5 , a g a r 0 x 1 , F ( y ) 0. 5 , a g a r 0 y 1 ,
1
2
1 , a g a r x 1 ,
1 , a g a r y 1.
( X , Y ) i k k i o ‗ lc ho vl i k t . m . ni n g F ( x , y ) taq s i m ot f u n k s iy a s ini ( 3.3.2) formulaga ko‗ra topamiz:
Y
X
y 0
x 0
0 y 1
0 x 1
0
y 1
x 1
0
0
0
1
0
1 1 2
1 1 2
6
1 1 2 2 1
2 6 6
2 6 6
6 6 6 6
3.4 Ikki o‘lchovlik uzluksiz tasodifiy miqdor zichlik funksiyasi va uning xossalari
- Ikki o‗lchovlik t.m. uzluksiz deyiladi, agar uning taqsimot funksiyasi
F ( x , y ) : 1. u z l u k s iz b o ‗ l s a ;
2. har bir argumenti bo‗yicha differensiyallanuvchi;
3. F ( x , y ) ikkinchi tartibli aralash hosila mavjud bo‗lsa.
''
xy
- Ikki o‘lchovlik (X,Y) t.m.ning zichlik funksiyasi
2 F ( x , y )
''
F ( x , y )
f ( x , y )
( 3 .4.1)
xy
x y
Tenglik orqali aniqlanadi.
( X , Y ) t. m .ning G s oh a g a( 2 3 -ras m ) t u s h ishi e hti m ol l i g i ( 3.3. 4 ) f o r m ulaga k o ‗ ra: P { x X x x , y Y y y }

F ( x x , y y ) F ( x , y y ) F ( x x , y ) F ( x , y ) ,
P { x X x x , y Y y y }
f
o ' r t ac h a
x y
1 F ( x x , y y ) F ( x , y y ) F ( x x , y ) F ( x , y ) .
y
x x
y 0 da li m itga o ‗ ta m i z ,
x 0 ,
F ' ( x , y
y ) F ' ( x , y )
x
x
lim f o'rtacha lim
x 0 y 0
y 0
,
y
'
'
' '
f ( x , y ) F ( x , y )
F ( x , y )
ya ‘ n i
.
x y
x
y
23-rasm.
Demak, ( X , Y ) ikki o‗lchovli tasodifiy vektorning zichlik funksiyasi deb,
P { x X x d x , y Y y d y } f ( x , y ) d x d y
( 3 .4.2)
tenglikni qanoatlantiruvchi funksiya ekan.

f ( x , y ) zichlik funkiyasi quyidagi xossalarga ega: 1. f ( x , y ) 0 .
2. P { ( X , Y ) D } f ( x , y ) d x d y .
(3.4.3)
D
3. F ( x , y ) f ( u , v ) dud v .
4. f ( x , y ) d x d y 1 .
5. X va Y t . m .l a r ning b i r o ‗ lchovl i k tengliklar yordamida topish mumkin:
x y
( 3 .4. 4 )
zichlik funksiyalarini quyidagi
f ( x , y ) d y f X ( x ) ; f ( x , y ) d x f Y ( y ) .
( 3 .4.5)
Isboti. 1. Bu xossa F ( x , y ) funksiyaning har qaysi argumenti bo‗yicha kamaymaydigan funksiya ekanligidan kelib chiqadi.
2. f ( x , y ) dxdy ifoda ( X , Y ) tasodifiy nuqtaning tomonlari dx va dy bo‗lgan to‗g‗ri to‗rtburchakka tushish ehtimolligini bildiragi. D sohani to‗g‗ri to‗rtburchaklarga ajratamiz(24-rasm) va har biri uchun (3.4.2) formulani qo‗llaymiz:
P {( X , Y ) D } f ( x i , y i ) x y
i 1
b o ‗ ladi. li m itga o ‗ tib,
n
E ndi da
x 0 , y 0
P { ( X , Y ) D } f ( x , y ) d x d y
D
qilamiz.
ni h o s il
24-rasm.
3. (3.4.3) formuladan:
F ( x , y ) P { X x , Y y } P { X x , Y y } f ( u , v ) dudv .
x y

4. F ( , ) 1 va ( 3 .4. 4 ) f o r m ulada x y d e b ma‘nosida),
F ( , ) f ( x , y ) d x d y 1 .
5. Avval X va Y t.m.larning taqsimot funksiyalarini topamiz:
olsak(limit
x
x
F X ( x ) F ( x , ) f ( u , v ) dudv f ( u , y ) dy du ,
(3.4.5)
y
y
F Y ( y ) F ( , y ) f ( u , v ) dudv f ( x , v ) dx dv .
Birinchi tenglikni x bo‗yicha, ikkinchisini y bo‗yicha differensiyallasak, X av Y t.m.larnin zichlik funksiyalarini hosil qilamiz:
f ( x ) F ' ( x ) f ( x , y ) dy
X X
va
f ( y ) F ' ( y ) f ( x , y ) dx .
Y Y
■
Izoh . Agar X va Y t.m.larning alohida zichlik funksiyalari berilgan
bo‗lsa, (umumiy holda) ularning birgalikdagi zichlik funksiyalarini topish mumkin emas.
3.3-misol. ( X , Y ) ikki o‗lchovli t.m.ning birgalidagi zichlik funksiyasi berilgan
C e - x - y , a g a r x 0 , y 0
f ( x , y )
0, aks holda.
Quyidagilarni toping: 1) O‗zgarmas son C; 2) F ( x , y ) ; 3) F X ( x ) va F Y ( y ) ; 4) f X ( x ) va f Y ( y ) ; 5) P { X 0, Y 1} .

1) f ( x , y ) d x d y 1 ten g likd a n
C e x y d x d y C e x d x e y d y C 1.
0 0 0 0
x y x y
2) F ( x , y ) e u v dud v e u d u e v d v ( 1 e x ) ( 1 e y ) , x 0 , y 0 ,
0 0 0 0
ya‘ni
x 0, y 0, aks holda.
( 1 e x ) ( 1 e y ) ,
F ( x , y )
0,
x
x
u
x
u v
3) F ( x ) F ( x , )
e e d v d u 1 e d u 1 e
, x 0 , de m a k
X
0 0
0
x 0 ,
x 0 .
( 1 e x ) ,
F X ( x )
0,
Aynan shunday,
y 0 ,
y 0 .
( 1 e y ) ,
F Y ( x )
0,
x 0 ,
x 0 ,
( 1 e x ) ' ,
x 0 ,
e x ,
'
x
( x ) F ( x )
4) f X
X
x 0, 0,
0,
va shu kabi
y 0,
0, y 0.
e y ,
f Y ( y )
1
1
- y
x
1
x
P { X 0, Y 1} e dx e dy
( e 1 ) e d x 1 0 . 63 .
5)
e
0
0
0

3.5 Tasodifiy miqdorlarning bog‘liqsizligi
- X va Y t.m.lar bog‘liqsiz deiladi, agar x , y R uchun { X x } va
{ Y y } hodisalar bog‗liqsiz bo‗lsa.
Endi t.m.lar bog‗liqsizligining zarur va yetarli shartini keltiramiz.
Teorema. X va Y t.m.lar bog‗liqsiz bo‗lishi uchun
F ( x , y ) F X ( x ) F Y ( y )
( 3 .5.1)
tenglik bajarilishi zarur va yetarlidir.
Isboti. Zarurligi. Agar X va Y t.m.lar bog‗liqsiz bo‗lsa, { X x } va
ho d i s a lar h am b o g ‗ l i q s iz b o ‗ la d i. U ho l da
{ Y y }
P { X x , Y y } P { X x } P { Y y } , ya‘ni F ( x , y ) F X ( x ) F Y ( y ) .
Yetarliligi. (3.5.1) tenglik o‗rinli bo‗lsin, u holda P { X x , Y y } P { X x } P { Y y } bo‗ladi. Bu tenglikdan X va Y t.m.lar bog‗liqsizligi kelib chiqadi. ■
1-natija. X va Y uzluksiz t.m.lar bog‗liqsiz bo‗lishi uchun
f ( x , y ) f X ( x ) f Y ( y )
( 3 .5.2)
tenglik bajarilishi zarur va yetarlidir.
Isboti. Zarurligi. Agar X va Y t.m.lar bog‗liqsiz bo‗lsa, u holda (3.5.1) tenglik o‗rinli bo‗ladi. Bu tenglikni x bo‗yicha, keyin esa y bo‗yicha
f ( x , y ) d F ( x ) d F ( y )
differensiyallab,
ten g l i klar n i, ya ‘ n i
X Y
d x d y
f ( x , y ) f X ( x ) f Y ( y ) ho s i l qil a m iz.
Yetarliligi. (3.5.2) tenglik o‗rinli bo‗lsin. Bu tenglikni x bo‗yicha va
y bo‗yicha integrallaymiz:
x y x y
f ( u , v ) dud v f X ( u ) d u f Y ( v ) d v .
Bu esa F ( x , y ) F X ( x ) F Y ( y ) tenglikning o‗zidir. Teoremaga ko‗ra X va
Y t.m.lar bog‗liqsizligi kelib chiqadi. ■

2-natija. X va Y diskret t.m.lar bog‗liqsiz bo‗lishi uchun ihtiyoriy
i 1 , 2 , .. . n , j 1 , 2 , .. . m larda
( 3 .5.3)
P { X x i , Y y j } P { X x i } P { Y y j }
tengliklarning bajarilishi zarur va yetarlidir.
3.4-misol. a) 3.1-misoldagi X va Y t.m.lar bog‗liqmi? b) 3.3- misoldagi X va Y t.m.lar bog‗liqsizmi?
P { X 0 , Y 0 } 1 , P { X 0 } P { Y 0 } 1 1 1 , ya ‘ n i
a) p
11
6 2 2 4
P { X 0, Y 0} P { X 0} P { Y 0} . Demak, X va Y t.m.lar bog‗liq.
x 0 ,
x 0 ,
e - x - y , a g a r x 0 , y 0 e x ,
f ( x , y )
f X ( x )
b)
0, aks holda, 0,
y 0,
0 , y 0 .
e y ,
f ( y )
f ( x , y ) f X ( x ) f Y ( y ) ten g l i k o ‗ r i n li, d e m a k, X va Y
Y
t.m.lar bog‗liqsiz.
3.6 Shartli taqsimot qonunlari
( X , Y ) ikki o‗lchovlik t.m.ni tashkil etuvchi X va Y t.m.lar bog‗liq bo‗lsa, ularning bog‗liqligini xarakterlovchi shartli taqsimot qonunlari tushunchalari keltiriladi.
- ( X , Y ) ikki o‗lchovli diskret t.m. birgalikdagi taqsimot qonuni
p ij P { X x i , Y y j } , i 1, n , j 1, m bo‗lsin. U holda
P { X x i , Y y j }
P { Y y j / X x i }
i 1 , 2 , .. . n , j 1 , 2 , .. . m
,
( 3 .6.1)
P { X x }
i
p ( y 1 / x i ) , p ( y 2 / x i ) , . . . p ( y m / x i ) lar Y t. m .ning
ehtimolliklar to‗plami, ya‘ni
X x i dagi shartli taqsimot qonuni deyiladi. Bu yerda
p
1
m m
m
p ij
i j j 1
i
x
p
1
p ( y / x )
.
i
j
p p
p
j 1 j 1
x i
x i
x i
Xuddi shunday,

P { X x i , Y y j }
P { X x i / Y y j }
i 1 , 2 , .. . n , j 1 , 2 , .. . m
, ( 3 .6. 2 )
P { Y y }
i
p ( x 1 / y j ) , p ( x 2 / y j ) , ... p ( x n / y j ) lar X t . m . ning
ehtimolliklar to‗plami, ya‘ni
dagi shartli taqsimot qonuni deyiladi.
3.5-misol. ( X , Y ) ikki o‗lchovlik t.m.ni birgalikdagi taqsimot jadvali
Y y j
berilgan:
Quyidagilarni toping: a) X av Y t.m.larning alohida taqsimot qonunlari; b) X t.m.ning Y=2 dagi shartli taqsimot qonuni.
X \ Y
1
0.1
0.12
2
0.2
0.16
3
0.08
0.40
0.10
0.14
m n
a ) p x p ij
i
j 1
va p y p ij
j
i 1
tengliklardan:
X
P
0.1
0.2
0.60
0.40
Y
1
P
2
0.28
3
0.10
0.54
,
b) (3.6.2) formulaga asosan: P { X 0.1/ Y 2} 0.08 4 ,
0.1 8 9
P { X 0.2 / Y 2} 0.10 5 . X t.m.ning Y=2 dagi shartli taqsimot qonuni
0.1 8 9
quyidagiga teng:
X
P Y 2
0.1
4
0.2
5
9
9
Endi ( X , Y ) ikki o‗lchovli t.m. uzluksiz bo‗lgan holni ko‗ramiz.
f X ( x ) va f Y ( y ) lar
f ( x , y ) ( X , Y ) t.m.ning birgalikdagi zichlik funksiyasi,
esa X va Y t.m.larning alohida zichlik funksiyalari bo‗lsin.
- Y t.m.ning X = x bo‗lgandagi shartli zichlik funksiyasi
f ( x , y )
f ( y / x ) f ( x , y ) , f ( x ) 0
( 3 .6.3)
X
f ( x , y ) dy
f ( x )
X
ifodaga orqali aniqlanadi.

f ( y / x ) 0 , f ( y / x ) d y 1
Shartli zichlik funksiyasi zichlik funksiyasining kabi xossalariga egadir.
- Xuddi shunday, X t.m.ning Y = y bo‗lgandagi shartli zichlik funksiyasi
f ( x , y )
f ( x / y ) f ( x , y ) , f ( y ) 0 ,
( 3 .6.4)
y
f ( x , y ) dx
f ( y )
Y
tenglik orqali aniqlanadi.
(3.6.3) va (3.6.4) tengliklarni hisobga olib, f ( x , y ) zichlik funksiyani
quyidagi ko‗rinishda yozish mumkin:
f ( x , y ) f X ( x ) f ( y / x ) f Y ( y ) f ( x / y ) .
( 3 .6. 5 )
( 3 .6. 5 ) tenglik z i c hl i k fun k s iy a lar n ing k o ‗ p ay tir is h q oi d a s i ( te o re m a s i) deyiladi.
3.6-misol. ( X , Y ) ikki o‗lchovli uzluksiz t.m.ning birgalikdagi zichlik
f u n k s iy a s i b er ilg an : f ( x , y ) C x y , a g a r ( x , y ) D ,
0 , a g a r ( x , y ) D ,
25 - ras m .
bu yerda D {( x , y ) : y x , y 2, x 0} (25-rasm). 1) toping. 2) X va Y t.m.larning bog‗liqligini ko‗rsating.
1) Avval o‗zgarmas son C ni topamiz:
f X ( x ) v a f ( x / y ) lar n i

0
2
0
0
x 2
y 2
C x 2 d x 2 C .
2
1
f ( x , y ) d x d y d x C xy d y C x d x
x
2
2
2
2
2 x
f X ( x ) ni topa m i z :
Bundan C 1 .
2
0
1
4
1
f X ( x ) f ( x , y ) d y x y d y
x ( 4 x 2 ) , x ( 2 , 0 ) .
2
2
f ( x / y ) ni (3.6.4) formulasidan foydalanamiz, buning uchun dastlab ni hisoblash kerak:
f Y ( y )
y 3
4
0
1
f ( y ) f ( x , y ) dx xy dx
,
,
y ( 0 , 2 )
Y
2
y
- 1 xy
2
f ( x / y ) f ( x , y )
2 x , ( x , y ) D .
y 3
y 2
f ( y )
Y
4
t. m . l a r
bog‗liqsiz
bo‗lsa,
2) X va Y
f ( x / y ) f ( x , y ) f X ( x ) f Y ( y ) f
tenglik
o‗rinli.
( x )
X
f Y ( y ) f Y ( y )
f
( x ) 1 x (4 x 2 ) , x ( 2, 0) va f ( x / y ) 2 x , ( x , y ) D funksiyalarlar
y 2
X
4
bir-biridan farqli bo‗lganligi uchun X va Y t.m.lar bog‗liq.
3.7 Ikki o‘lchovli tasodifiy miqdorlarning sonli xarakteristikalari
( X , Y ) tasodifiy vektorning sonli xarakteristikalari sifatida turli tartibdagi momentlar ko‗riladi. Amaliyotda eng ko‗p I va II – tartibli momentlar bilan ifodalanuvchi matematik kutilma, dispersiya va korrelatsion momentlardan foydalaniladi.
- Ikki o‗lchovli diskret ( X , Y ) t.m.ning matematik kutilmasi ( MX , MY ) bo‗lib, bu yerda

MX m x x i p ij ,
MY m y y i p ij
i 1 j 1
i 1 j 1
n m
n m
( 3 .7.1)
va p ij P { X x i , Y y j } .
Agar ( X , Y ) t.m. uzluksiz bo‗lsa, u holda
M X m x x f ( x , y ) d x d y ,
M Y m y y f ( x , y ) d x d y .
(3.7.2)
- X va Y t.m.larning kovariatsiyasi
K X Y c o v ( X , Y ) M ( X m x ) ( Y m y ) 1 , 1
t e ngl i k bil a n a n i qlanad i . Agar ( X , Y ) t. m . diskr e t kovariatsiyasi
(3.7.3)
bo‗lsa,
un i ng
K XY ( x i m x ) ( y j m y ) p ij ,
i 1 j 1
n m
( 3 .7. 4 )
agar uzluksiz bo‗lsa,
K X Y ( x m x ) ( y m y ) f ( x , y ) d x d y
( 3 .7. 5 )
formulalar orqali hisoblanadi.
Kovariatsiyani quyidagicha hisoblash ham mumkin:
K X Y c o v ( X , Y ) M X Y MX M Y .
( 3 .7. 6 )
Bu tenglik (3.7.3) formula va matematik kutilmaning xossalaridan kelib chiqadi:
K X Y M ( X m x ) ( Y m y ) M ( X Y X m y Y m x m x m y )
MXY m y MX m x MY m x m y MXY m y m x m x m y m x m y MXY MXMY .
Kovariatsiya orqali X va Y t.m.larning dispersiyalarini aniqlash mumkin:
D X c o v ( X , X ) M ( X M X ) 2 M X 2 ( M X ) 2 ,
D Y c o v ( Y , Y ) M ( Y M Y ) 2 M Y 2 ( M Y ) 2 .
( X , Y ) vektorning kovariatsiya matritsasi
C M ( X , Y ) ( X , Y ) ( m , m ) ( m , m )
x y x y
DX
c o v ( Y , X ) D Y
K XY
K YX K YY
c o v ( X , Y ) K X X
- ifoda bilan aiqlanadi.
Kovariatsiyaning xossalari:
- K XY K YX ;
- Agar X Y b o ‗ l sa , u h o l d a K X Y 0 ;
- Agar X va Y i x ti y or i y t. m .l a r b o ‗ l s a , u h o l da D ( X Y ) D X DY 2 K X Y ;
y oki c o v ( C X , Y ) C c o v ( X , Y ) c o v ( X , C Y ) ;
4. K CX , Y CK XY K X , CY
y oki
5 . K X C , Y K X Y K X , Y C K X C , Y C
c o v ( X C , Y ) c o v ( X , Y ) c o v ( X , Y C ) c o v ( X C , Y C ) ;
X Y .
6. K XY
Isboti. 1. (3.7.3) dan kelib chiqadi.
2. Agar X Y bo‗lsa, u holda X m x va Y m y lar ham bog‗liqsiz bo‗ladi
va matematik kutilmaning xossasiga ko‗ra K XY 0 .
3. D ( X Y ) M (( X Y ) M ( X Y )) 2 M (( X MX ) ( Y MY )) 2
M ( X MX ) 2 2 M ( X MX )( Y MY ) M ( Y MY ) 2 DX DY 2 K .
XY
4. K CX , Y M ( CX MCX )( Y MY ) M C ( X MX )( Y MY ) CK XY .
5. K X C , Y M (( X C ) M ( X C ))( Y MY ) M ( X C MX C )( Y MY )
M ( X M X ) ( Y M Y ) K XY
X m x
Y m y
t.m.larga qo‗llasak,
6 . 3 - x o s s a ni va
x
y
m Y m
Y m
X m
X
y
y
- D
D
D
x
x
x
y
y
x

Y m y
X m Y m y
X m
x
M
2 M
x M
x y
y
x
X m Y m
1 1 2 M x y 2 1
K
XY
.
X Y
y
x
K XY
X Y . ■
Disp e r siya ma nf i y b o‗ l m a s lig i d a n 2 1 0 , ya ‘ n i K X Y
X Y
3-xossaga ko‗ra, agar K XY 0 bo‗lsa, X va Y t.m.lar bo‗gliq bo‗ladi.
B u h o l da X va Y t. m .l a r kor r e lats iy a lan g a n d ey il a di. L e kin
K XY 0
ekanligidan X va Y t.m.larning bog‗liqsizligi kelib chiqmaydi. Demak, X va Y t.m.larning bog‗liqsizligida ularning korrelatsiyalanmaganligi kelib chiqadi, teskarisi esa har doim ham o‗rinli emas.
- X va Y t.m.larning korrelatsiya koeffitsienti
c o v ( X , Y )
K XY
r
( 3 .7. 7 )
XY
D X D Y
X Y
formula bilan aniqlanadi.
Korrelyatsiya koeffisiyentining xossalari:
- r X Y 1 , y a ‘ n i 1 r X Y 1 ;
- Agar X Y b o ‗ l s a , u h o l d a r X Y 0 ;
3. Agar 1 bo‗lsa, u holda X va Y t.m.lar chiziqli funksional bog‗liq
r XY
bo‗ladi, teskarisi ham o‗rinli.
Shunday qilib, bogliqsiz t.m.lar uchun r XY 0 , chiziqli bog‗langan
1 r XY 1 . Agar 0
b o ‗ l s a ,
t.m.lar uchun 1 , qolgan hollarda
r XY r XY
t.m.lar musbat korrelatsiyalangan va aksincha manfiy korrelyatsialangan deyiladi.
r XY 0
a g a r
bo‗lsa, ular
3.8 Ba’zi muhim ikki o‘lchovlik taqsimotlar
Doiradagi tekis taqsimot . Radiusi R 1 bo‗lgan doirada X , Y t.m. tekis taqsimotga ega bo‗lsin(26-rasm).

y
1
1
O
1
x
1
26-rasm.
Demak, (X,Y) ning birgalikdagi zichlik funksiyasi
C , a g a r x 2 y 2 1 ,
f x , y
0 , a g a r x 2 y 2 1.
O‗zgarmas C ni
1 1 x 2
f x , y d x dy 1 , ya ‘ n i
C d x d y 1
1 1 x 2
shartdan aniqlaymiz. Bu karrali integralni geometrik ma'nosidan kelib chiqqan holda hisoblash osonroq(27-rasm).
27 - ras m .

f x , y sirt va OXY tekislik bilan chegaralangan jismning hajmi 1 ga tengdir. Bizning holda bu asosi R 2 1 2 va balandligi C bo‗lgan
silindr hajmidir V C 1 . Dеmаk, C 1 vа izlаnаyotgаn zichlik funksiyasi
1 , a g a r x 2 y 2 1 ,
f x , y
0 , a g a r x 2 y 2 1 .
Ungа mоs taqsimot funksiyani hisоblаymiz:
x y x y
F x , y f u , v dudv
1
dud v .
1 1 u 2
28-rаsm.
Tаbiiyki, bu intеgrаl x 2 y 2 1 dоirа bilаn uchi M nuqtаdа bo‗lgаn
1
D a , b R 2 : a x , b y - kv аd rаn t ning
аniqligidа kеsishishidаn hоsil
bo‗lgаn sоhа D 0 yuzаsigа tеngdir(28-rаsm). Tаbiiyki, x 1, y dа
F x , y 0 , chunki bu hоldа D 0 , endi x 1 vа y 1 dа F x , y 1 , chunki bu hоldа D 0 - sоhа x y 1 dоirа bilаn ustmа-ust tushаdi.
2 2
Endi X vа Y lаrning mаrginаl taqsimot funksuyalаri F X vа F Y lаrni hisоblаymiz: 1 x 1 dа

x
1 1 u 2
1 u
x
x
x 1 u 2
1
1
F x
f u , v dudv
du 2 1 u 2 du
dudv v
2
X
1
1
1 1 u 2
1 1
1
x
2
2
x 1 x arc s in u
x 1 x arc s in x .
1
2
Dеmаk,
0 ,
1
agar x -1,
- x 1 x a r c sin x , a g a r 1 x 1 ,
1
F X x
2
2
1,
a g a r x 1 .
Аynаn shungа o‗хshаsh
0 ,
1
agar y -1,
- y 1 y arc s i n y , a g a r 1 y 1 ,
1
F Y y
2
2
1 , a g a r y 1 .
Nihоyat, X vа Y lаrning mаrginаl zichliklаrini hisоblаymiz:
1 x 2 1
x f x , y d y
2
1 x 2
2
f X
1 x 1 ,
dy 1 x ,
vа shu kаbi
f Y y f x , y d x
1 y 2
1 y 2
1 2 2
dx 1 y ,
1 y 1 .
Ko‗rinib turibdiki, f x , y f X x f Y y , dеmаk, X vа Y bоg‗liq t.m.lаr ekаn. Shuni tа‘kidlаb o‗tish lоzimki, tеkis tаqsimоtgа egа bo‗lgаn hаr qаndаy X , Y juftlik dоimо bоg‗liq bo‗lаdi dеb аytish nоto‗g‗ridir. Chunki X vа Y lаrning bоg‗liqlik хоssаlаri ulаr qаndаy sоhаdа tеkis tаqsimоtgа
egа ekаnligigа bоg‗liqdir. Shu bоisdаn kеyingi tаqsimоtni ko‗rib o‗tаmiz.
Kvаdrаtdаgi tеkis tаqsimоt . X , Y juftlik 0,1 0,1 kvаdrаtdа tеkis tаqsimоtgа egа bo‗lsin. U hоldа ulаr birgаlikdаgi taqsomot funksiyasi ko‗rinishi quyidаgidеk bo‗lаdi:
0, x , y 0,
F x , y x y , 0 x , y 1 ,
1 , x , y 1.
B und а n
0, x 0,
F x F x , F x , 1 x , 0 x 1 ,
X
1 , x 1 .
0, y 0,
F y F , y F 1 , y y , 0 y 1 ,
Y
1 , y 1 .
x , y R lаr u c hun F x , y F x F y , ya ‘ n i vа
Dеmаk, bаrchа
X Y bоg‗liq
1
X Y
emаs ekаn.
Ikki o‘lchоvlik nоrmаl(Gаuss) tаqsimоti . X , Y tаsоdifiy vеktоr
i k k i o ‗ lchоvli n о r m а l tаq s i m оt g а e gа b o ‗ lsin. U h о l dа X , Y n in g birgаlikdаgi zichlik funksiyasi
1 x a 2 x a y a y a 2
1
f x , y
exp
1 2 r 1 2 2 .
2
2
2
2 1
2 1 r 2
1
2
1
2
1 2
G е о m е t r ik n u qt а y i n аzа r d а n f x , y grаf i gi c h o ‗ q q i s i a 1 , a 2 nu q tа d а jоylаshgаn « tоg‗ » shаklini bildirаdi(29-rаsm). Аgаrdа biz bu tоg‗ni OXY tеkisligigа паrаllеl tеkislik bilаn kеsаdigаn bo‗lsаk, u hоldа kеsilish chiziqlаri quyidаgi ellipslаrdаn ibоrаt bo‗lаdi:
x a y a
2
2
y a
x a
C -kоnstаntа, bu yеrdа a MX ,
1
1 2
2
2 r
1
2
2
2
1 2
1
2
M Y , D X
, 2 DY , vа r r -kоrrеlatsiya kоeffitsiеntidir.
a
2 1
2 X , Y
Аgаr r 0 bo‗lsа, bu chiziqlаr аylаnаlаrdаn ibоrаt bo‗lib qоlаdi. Biz r ning аynаn kоrrеlatsiya kоeffisiеnti bo‗lishigа ishоnch hоsil qilish mаqsаdidа

X a 1
Y a 2
vа Z
Z
2
2
1
2
1
2
ya ngi t. m . l а r n i ki r i t а m iz. T а b ii y ki, M Z k 0 , D Z k 1 , k 1 , 2 . U hо l dа Z 1 , Z 2
ning zichlik funksiyasi
1
2 1 r 2
2
2
z 2 r z z z
e x p
g z , z
1 1 2
2
.
2 1 r 2
1 2
29-rаsm.
Endi kоrrеlatsiya kоeffitsiеntini hisоblаymiz:
1
z z g z , z dz dz
2 1 2 1 2 1 2
r X , Y Cov Z 1 , Z 2 M Z 1 Z 2
2 1 r
2
z 2 2
1 2 1 r 2
z rz
z
1 2
z e 2
- rz rz e xp
dz dz
1 2
2
1 2 2
2
2 1 r
2
z 2 2
1
2
z r z
1
z e 2
z
r z d z
1 2
d z
- rz exp
1 2 2
2
1 2
2
2 1
- r
2 1 r 2
2
z 2 2
z r z
1
r
z 2 e 2 exp
r .
r z d z
1 2
d z
1 2 2
2
2
2
- r
2 1
2 1 r 2

Охirgi tеnglikni hоsil qilishdа quyidаgi intеgrаllаrdаn fоydаlаndik:
u 2
2 1 r 2
1
2
u e
u z 1 r z 2 ,
du 0,
2 1 r
-mаrkаzlаshtirilgаn nоrmаl t.m.ning mаtеmаtik kutilmаsi;
u 2
2 1 r 2
1
2
e
d u 1 , u z 1 r z 2 ,
2 1 r
-zichlik funksiya intеgrаli;
z 2 2
1
2
z e d z 1 ,
2
2 2
2
-stаndаrt nоrmаl t.m. dispеrsiyasi.
Dеmаk, r X , Y r ekаn. Аgаr ikki nоrmаl tаqsimоtgа egа bo‗lgаn X
bo‗lishi r ning хоssаsidаn kеlib
vа t.m.lаr bоg‗liq bo‗lmаsа,
Y r 0
chiqаdi. Endi shu t.m.lаr uchun r 0 bo‗lsin. U hоldа
1 x a 2 y a 2
1
f x , y
x f y ,
exp
1 2 f
X
Y
2
2
2
2
1
2
1 2
bu yеrdа
y a
x a
2
1
2
1
y exp
f x e xp
2
1
, f Y
2
X
2
2
2 2
2
2
1
2
1
funksiyalаr
nоrmаl t.m.lаr zichlik funksiyalаridir.
N a , , N a ,
2 2
1 1 2 2
Dеmаk, t.m.lаr kоrrеlyatsiyalаnmаgаnligidаn ulаrning bоg‗liqsizligi hаm kеlib chiqаr ekаn. Bu hоl ikki o‗lchоvlik nоrmаl tаqsimоtni bоshqа tаqsimоtlаrdаn аjrаtib turаdi.

3.9 Xarakteristik funksiyalar va uning xossalari
Taqsimot funksiya bilan bir qatorda u haqidagi hamma ma‘lumotni o‗z ichiga oluvchi xarakteristik funksiyalardan ham foydalaniladi. Xarakteristik funksiya yordamida bog‗liqsiz t.m.larning yig‗indisining taqsimotini topish, sonli xarakteristikalarni hisoblash bir muncha osonlashadi.
e itX t.m.ning
- X t.m.ning xarakteristik funksiyasi
m a t e m a tik
ku t il m a s i b o ‗ l i b, uni X ( t ) y oki ( t ) or q a li b e l g il a y m i z . S hu n d a y qili b , ta‘rifga ko‗ra:
( t ) Me itX .
( 3 .9.1)
x 1 , x 2 , . . . x n , . . . p k P { X x k }, k 1 , 2 , . . .
Agar X t.m. qiymatlarni
e hti m olli k lar bil a n q a bul qi l uv ch i d i s kret t. m . b o ‗ l s a , u h o l d a u ning xarakteristik funksiyasi
( t ) e it x k p
( 3 .9.2)
k
k 1
formula orqali, agar zichlik funksiyasi f ( x ) bo‗lgan uzluksiz t.m. bo‗lsa, u holda uning xarakteristik funksiyasi
( t ) e it x f ( x ) d x
( 3 .9.3)
formula orqali aniqlanadi.
Xarakteristik funksiyaning xossalari:
- B a rcha t R u c hun quy i d a gi ten g s izlik o ‗ r i n l i :
( t ) ( 0 ) 1 .
- Agar Y aX b bo‗lsa, bu yerda a va b o‗zgarmas sonlar, u holda
Y ( t ) e X ( a t ) .
itb
- Agar X va Y t.m.lar bog‗liqsiz bo‗lsa, u holda X + Y yig‗indining xarakteristik funksiyasi X va Y t.m.larning xarakteristik funksiyalari ko‗paytmasiga teng:
X Y ( t ) X ( t ) Y ( t ) .
4. Agar X t.m.ning k -tartibli boshlang‗ich momenti k MX mavjud
k
bo‗lsa, u holda unga mos xarakteristik funksiyaning k -tartibli hosilasi mavjud bo‗lib, uning t =0 dagi qiymati
( 0) i M ( X ) i
( k ) k k k
.
X
Is b ot i . 1. ( t ) M e it X M 1 1 , c hunki
k
M e itX
e itX
co s t X i si n t X c o s 2 t X s i n 2 t X 1 . ( 0) M e 0 M 1 1 .
- Y ( t ) M e M e M ( e e ) e M e e ( a t ) .
itY it ( aX b ) itb iaXt itb iatX itb
X
- X Y ( t ) M e M ( e e ) M e M e ( t ) ( t ) . B u xo ss a n
it ( X Y ) itX itY itX itY
X Y
ta bog‗liqsiz tasodifiy miqdorlar yig‗indisi uchun ham o‗rinlidir.
d k M e i t X
( k )
k k itX
( t ) i M ( X e
4. Hisoblashdan ko‗rinadiki,
) . Demak t =0
X
dt k
( 0) i M ( X ) i
bo‗lsa,
. ■
( k ) k k k
X
k
i ( 0)
4-xossadan
.
k ( k )
k X
1 MX i (0) ; MX (0) ;
' 2 ''
2
(3.9.4)
(0))
DX ( 0) (
.
2 ' '
'
2
2 1
3.7-misol. Agar X Bi ( n ; p ) bo‗lsa, u holda X t.m.ning xarakteristik funksiyasi, matematik kutilmasi va dispersiyasini toping.
X t.m. 0,1,2,…,n qiymatlarni
p P { X k } C k p k q n k k 0 , 1 , .. . , n
k n
ehtimolliklar bilan qabul qiladi. (3.9.2) va Nyuton binomi formulalaridan
n n
n n
( t ) e C p q C ( e p ) q ( e p q )
k it k n k it n
itk k k n k
foydalansak,
, y a ‘ ni X
k 0 k 0
t.m.ning xarakteristik funksiyasi ( t ) ( e it p q ) n ifoda bilan aniqlanishiga
ishonch hosil qilamiz. (3.9.4) formulaga
M X i ( n ( e i t p q ) n 1 p e i t i ) n p va s hu kabi D X np q .
t 0
ko‗ra:
3.8-misol. Agar bo‗lsa, u holda X ning xarakteristik
X N ( a , )
funksiyasi, matematik kutilmasi va dispersiyasini toping.
e it x e
( x a ) 2
1
( t )
dx
2 2
(3.9.3) formulaga asosan:
2
x 2 2 x ( a i t 2 ) ( a i t 2 ) 2 a 2 ( a i t 2 ) 2
x 2 2 ( a i t 2 ) x a 2
1
1
e
e
dx
dx
2 2
2 2
2
2
2 ai t 2 ( i t 2 ) 2
( x ( a i t 2 ) ) 2
2 ai t 2 t 2 4
( x ( a i t 2 ) ) 2
1
1
e
e
e
d x
e
d x
2 2
2 2
2 2
2 2
2
2
x ( a i t 2 ) 2
2 e
2 2
2 2
2 2
x ( a i t 2 )
1
1
i a t t
i a t t
i a t t
2
2
d
2
e
2 e
e
2
2
2
u
e du
b o ‗ l s a ,
P u a sso n i n t e gr al i . S h u n d a y qil i b, aga r
t 2 2
X N ( a , )
ia t
u ho l da ( t ) e
m a t e m a tik kutil m a s i va
. Endi X t.m.ning
hisoblaymiz.
t 2 2
2
dispersiyasini
M X i ' ( 0 ) i e iat ( i a t 2 ) i 1 i a a ,
2
t o
t 2 2
t 2 2
2
iat
D X ' ' ( 0) ( ' (0 ) ) 2 2 e
- ( ia t 2 ) 2 e iat
( i a ) 2
2
t o
2 i 2 a 2 i 2 a 2 2 .
III bobga doir misollar
1 . ( X , Y ) i kki o ‗ lchovli u z luk s iz t. m .ning b i r g a l i kd ag i z ichlik f u n k s iy a s i b o ‗ l s a ,
C
f ( x , y )
k o ‗ r i n i s h i da b e r i l g a n
( 1 x 2 ) ( 1 y 2 )
quyidagilarni toping:
1) o‗zgarmas son C; 2) F ( x , y ); 3) P { X Y f ( x )va f ( y ).
2. Agar ( X , Y ) vektor taqsimoti quyidagicha bo‗lsa:
Y
0
-1
0
0.1
1
0.2
0.2
1
0.3
0.1
0.1
Z XY ning matematik kutilmasini hisoblang.

3. ( X , Y ) ikki o‗lchovlik uzluksiz t.m. uchlari O (0,0), A (0,4), B (4,0) nuqtalarda bo‗lgan uchburchak ichida tekic taqsimlangan(ya‘ni f ( x , y )= c ). Quyidagilarni hisoblang: 1) birgalikdagi zichlik funksiyasi f ( x , y ); 2) f ( x )va f ( y ); 3) A ={0X Y
0 x 1 , 0 y 1 , аks holda
f ( x , y ) x y ,
4 . ( X , Y ) tas o d i f i y v e k t or z i c hl i gi
bo‗lsa, MX va MY larni hisoblang.
0,
5 . А g a r ( X , Y ) tas o di f iy v e k t orni n g t a q s i m oti
b o ‗ l s a , u h o l da M ( X Y ) M X M Y ,
D ( X Y ) D X D Y 2 Co v ( x , y ) ten g l i k lar ekanligini ko‗rsating.
X
0
Y
0
1/8
1
1
1/4
2
0
1/8
1/8
3/8
o ‗ r i n li
6. Quyida ( X , Y ) ikki o‗lchovli uzluksiz t.m.ning birgalikdagi zichlik
f ( x , y ) C x y , a g a r ( x , y ) D ,
, b u er da D
f u n k s iy a s i b e r i l g a n :
0 , a g a r ( x , y ) D
teki sl i kd ag i quy i d a gi s h a r t la r ni q an o a tl a nt ir uv c hi s o h a :
y x ,
y 2,
O‗zgarmas son C ni toping, X va Y t.m.lar bog‗liq ekanligini
x 0.
ko‗rsating.
7. Agar
va X Y b o ‗ ls a , u h o l d a
X B i ( 2 ; 0 .2) , Y B i ( 1 ; 0 . 8 )
Z X Y t.m.ning taqsimot funksiyasini toping va F Z (1) ni hisoblang.
8. Аgar X va Y t.m.larning birgalikdagi taqsimoti
Y
-1
-1
X
1
0.05
0
0.1
0.3
1
0.05
0.15
2
0.25
0.05
0.05
bo‗lsa, u holda Z Y X vа U Y 2 X 2 larning taqsimotlarini toping.
9. ( X , Y ) ikki o‗lchovlik diskret t.m.ning birgalikdagi taqsimot jadvali berilgan:
X va Y t. m . lar bo g ‗ l iq yo ki bog‗liqsizligini tekshiring va cov( X , Y ) ni
hisoblang.
X \ Y
1
1
2
0.07
2
0.04
3
0.08
3
0.11
0.09
0.11
4
0.13
0.06
0.11
0.08
0.10
0.02

10. X va Y t.m.larning birgalikdagi zichlik funksiyasi berilgan:
a ( 1 x y 3 ) , a g a r x 1 , y 1 ,
f ( x , y )
0, aks holda.
O‗zgarmas son a va korrelatsiya koeffitsientini hisoblang.
11. X va Y t.m.larning birgalikdagi zichlik funksiyasi berilgan:
f ( x , y ) C ( x y ) , a g a r 0 x 1 , 0 y 1 ,
0, aks holda.
1) X va Y t.m.lar bog‗liqmi? 2) X va Y t.m.larning matematik kutilmasi va dispersiyasini hisoblang.
12 . ( X , Y ) tas o di f iy v e kt o r n in g bi r g a li k d a gi ta q s i m oti
0, x 0, y 0,
xy
F ( x , y ) 8 , 0 x 2 , 0 y 4 ,
1,
bo‗lsa, X vа Y o‗zaro bog‗liqmi?
x 2, y 2,
Y
1
1
X
1
2
2
1
0
3
3
1
3
13 . А g a r ( X , Y ) tas o di f iy v e ktor n i ng bi r g a l i kd a gi taqsimoti berilgan bo‗lsa, Cov ( X , Y ) ni hisoblang.
C o v ( X , Y ) ni
14. X R ( a , a ) bo‗lsa, X vа Y X 2 lar uchun
hisoblang. X va Y lar bog‗liqmi?
15. Аgar X vа Y bog‗liqsiz, bir xil taqsimlangan va
M X 2 , M Y 2
bo‗lsa, u holda Cov ( X Y , X Y ) 0 ekanini isbotlang.
16. Agar X E (1) , DY 2 va D ( X Y ) 3 bo‗lsa, r XY ni hisoblang.
2
1 1 1
3 3 3
X : 0
2
17 . А g a r
b o ‗ l s a , Y si n X v a Z c o s X u c hun
P :
X
Co v ( Y , Z ) 0 , am m o Y v a Z b o g ‗ l i q l i g i ni k o ‗ r s a ti n g .
18. Аgar ( X , Y ) zichlik funksiyasi x , y 0 bo‗lsa,
f ( x , y ) e x y ,
sh a r t l i z ichlik f u n k s iy a lar f x Y y va g y X x ni hiso b l a n g .
![19. Аgar ( X , Y ) tasodifiy vektorning birgalikdagi zichlik funksiyasi ( x , y ) [ 0 , 1 ] [ 0 , 1 ] , аks holda f ( x , y ) x 2 y , bo ‗ l s a , M Y X x n i x 1 d а 0, hisoblang. 20 . А g a r ( X , Y ) ni n g bi r g a li kda gi taq s i m oti b o ‗ l s a , r XY ni hisoblang . Y 1 1 X 2/9 2 2 1/9 1/9 3 3 2/9 0 0 1/9 1/9 1/9 21. Agar X va Y t.m.larning birgalikdagi zichlik funksiyasi x 2 4 y 2 1 f ( x , y ) e bo‗lsa, u holda ( X , Y ) tasodifiy nuqtaning 6 3 { x 1, y 2} sohaga tushishi ehtimolligini toping. [ a , b ] o raliqda tek i s taq s i m lan g a n X t. m .ning x a ra k teri s t i k funksiyasini toping. Agar X t.m. a parametrli Puasson taqsimotiga ega bo‗lsa, uning matematik kutilmasini xarakteristik funksiya yordamida hisoblang. X t.m.ning zichlik funksiyasi berilgan: f ( x ) 2 x , a g a r x [ 1 , 0] , ( t ) ni hisoblang. 0 , a g a r x [ 1 , 0] , X 25. Аgar X va Y t.m.larning birgalikdagi taqsimoti quyidagi jadval yordamida berilgan bo‗lsa, Р ( Х =1/ У =1), Р ( Х =0/ У =1), МХ va MY larni toping. X Y 0 0 1 1/4 1 1/8 1/8 2 1/8 1/8 1/4](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img93.jpg)
19. Аgar ( X , Y ) tasodifiy vektorning birgalikdagi zichlik funksiyasi
( x , y ) [ 0 , 1 ] [ 0 , 1 ] ,
аks holda
f ( x , y ) x 2 y ,
bo ‗ l s a ,
M Y X x
n i x 1 d а
0,
hisoblang.
20 . А g a r ( X , Y ) ni n g bi r g a li kda gi taq s i m oti b o ‗ l s a ,
r XY ni hisoblang .
Y
1
1
X
2/9
2
2
1/9
1/9
3
3
2/9
0
0
1/9
1/9
1/9
21. Agar X va Y t.m.larning birgalikdagi zichlik funksiyasi
x 2 4 y 2
1
f ( x , y ) e
bo‗lsa, u holda ( X , Y ) tasodifiy nuqtaning
6
3
{ x 1, y 2} sohaga tushishi ehtimolligini toping.
- [ a , b ] o raliqda tek i s taq s i m lan g a n X t. m .ning x a ra k teri s t i k funksiyasini toping.
- Agar X t.m. a parametrli Puasson taqsimotiga ega bo‗lsa, uning
matematik kutilmasini xarakteristik funksiya yordamida hisoblang.
- X t.m.ning zichlik funksiyasi berilgan:
f ( x ) 2 x , a g a r x [ 1 , 0] ,
( t ) ni hisoblang.
0 , a g a r x [ 1 , 0] ,
X
25. Аgar X va Y t.m.larning birgalikdagi taqsimoti quyidagi jadval yordamida berilgan bo‗lsa, Р ( Х =1/ У =1), Р ( Х =0/ У =1), МХ va MY larni toping.
X
Y
0
0
1
1/4
1
1/8
1/8
2
1/8
1/8
1/4
IV bob. Tasodifiy miqdorlarning funksiyalari
4.1 Bir argumentning funksiyalari
- Agar X t.m.ning har bir qiymatiga biror qoida bo‗yicha mos ravishda Y t.m.ning bitta qiymati mos qo‗yilsa, u holda Y ni X tasodifiy argumentning funksiyasi deyiladi va Y ( X ) kabi yoziladi.
X diskret t.m. qiymatlarni mos bilan qabul qilsin:
ehtimolliklar
Y ( X ) t. m .
x 1 , x 2 , ..., x n p 1 , p 2 , ..., p n
p i P { X x i }, i 1 , 2 , ... , n . R a v s h a nki,
h a m d i skret t. m . b o‗ ladi va u n i n g q a bul qil a d i g a n q iy ma tl a ri y 1 ( x 1 ) ,
y 2 ( x 2 ) ,…, y n ( x n ) , mos ehtimolliklari esa p 1 , p 2 ,..., p n bo‗ladi. Demak,
p i P { Y y i } P { Y ( x i ) } , i 1 , 2 , ... , n .
S h uni ta ‘ kidl a sh l o z i m ki, X
t.m.ning har xil qiymatlariga mos Y t.m.ning bir xil qiymatlari mos kelishi mumkin. Bunday hollarda qaytarilayotgan qiymatlarning ehtimolliklarini qo‗shish kerak bo‗ladi.
t . m .ning m a t e matik k ut i l m a s i va disp er siy a s i qu yida gi
Y ( X )
tengliklar orqali aniqlanadi:
n
n
M Y ( x ) p ,
( x ) M Y ) p
2
D Y (
i .
i i
i
i 1 i 1
4.1-misol. X diskret t.m.ning taqsimot jadvali berilgan:
X
p
-1
0.1
1
0.2
2
0.6
Agar: 1) Y X 2 ; 2) Y 2 X 1 0 b o ‗ l s a , M Y ni hiso b lan g .
1) Y t.m.ning qabul qiladigan qiymatlari:
y ( x ) ( 1 ) 1 ,
2
y 1 2 1 ,
1 1 2
y 3 2 4 , ya‘ni uning qabul qiladigan qiymatlai 1 va 4. Y t.m. X t.m.ning
2
-1 va 1 qiymatlarida 1 qiymat qabul qilganligi uchun
p 1 P { Y 1 } P { X 1 } P { X 1 } 0. 1 0 .3 0 .4 ,
Y : 1 , 4
p 2 P { Y 4} P { X 2} 0.6 . Demak,
M Y 1 0 . 4 4 0 . 6 2 . 8 .
va
P : 0 . 4 , 0 . 6
Y : 8 , 1 2 , 1 4
2) Y t.m.ning taqsimot qonuni quyidagi ko‗rinishga ega: P : 0.1, 0.3,
0 . 6 .
M Y 8 0 . 1 1 2 0 . 3 1 4 0 . 6 12 . 8 .

Zichlik funksiyasi f ( x ) bo‗lgan X uzluksiz t.m. berilgan bo‗lsin. Y t.m. e s a X t . m . ni n g fu nk s iy a s i Y ( X ) . Y t.m . ni n g ta q s i m ot i n i topa m i z . Y ( X ) funksiya X t.m.ning barcha qiymatlarida uzluksiz, ( a , b ) intervalda
y ( x )
q a t ‘ iy o ‗ s u v c hi v a di f feren s ia l lanu vc hi b o ‗ l s i n, u h ol d a
x ( y )
funksiyaga teskari funksiya mavjud. Y t.m.ning taqsimot
funksiyasi formula orqali
aniqlanadi. { Y y } hodisa
G ( y ) P { Y y }
{ X ( y ) } ho d i s a ga e kvi v a le n t ( 3 0 -ras m ) .
30-rasm.
Yuqoridagilarni e‘tiborga olsak,
( y )
G ( y ) P { Y y } P { X ( y )} F X ( ( y )) f ( x ) dx .
a
( 4 .1.1)
(4.1.1) ni y bo‗yicha differensiallaymiz va Y t.m.ning zichlik funksiyasini topamiz: g ( y ) G ( y ) f ( ( y )) d ( ( y )) f ( ( y )) ' ( y ) .
dy dy
Demak,
g ( y ) f ( ( y ) ) ' ( y ) .
( 4 .1.2)
Agar y ( x ) funksiya ( a , b ) intervalda qat‘iy kamayuvchi bo‗lsa, u holda
{ Y y } hodisa { X ( y )} hodisaga ekvivalent. Shuning uchun,

b ( y )
G ( y ) f ( x ) d x f ( x ) d x .
( y ) b
g ( y ) f ( ( y )) ' ( y ) (4.1.3)
Bu yerdan,
Zichlik funksiya manfiy bo‗lmasligini hisobga olib, (4.1.2) va (4.1.3) formulalarni umumlashtirish mumkin:
g ( y ) f ( ( y ) ) ' ( y ) .
( 4 .1.4)
Agar y ( x ) funksiya ( a , b ) intervalda monoton bo‗lmasa, u holda g ( y ) ni topish uchun ( a , b ) intervalni n ta monotonlik bo‗lakchalarga ajratish, har bi r i b o ‗ y icha te s k a ri f u n k s iy a s i i n i t op i s h va q u y i d ag i for m uladan foydalanish kerak:
n
g ( y ) f (
i 1
( y ) ) ( y )
'
. ( 4 .1.5)
i i
Agar X zichlik funksiyasi f ( x ) bo‗lgan uzluksiz t.m. bo‗lsa, u holda Y ( X ) t.m.ning sonli xarakteristikalarini hisoblash uchun Y t.m.ning taqsimotini qo‗llash shart emas:
M Y M ( ( X ) ) ( x ) f ( x ) d x ,
(4.1.6)
D Y D ( ( X ) ) ( ( x ) M Y ) 2 f ( x ) d x .
4.2-misol. X zichlik funksiyasi f ( x ) bo‗lgan uzluksiz t.m. bo‗lsa, Y = -
5 X +2 t.m.ning zichlik funksiyasini toping.
f u n k s iya i n ter v a l d a m onot o n k a m ay uv c hi.
y 5 x 2
( ; )
x 1 ( 2 y ) ( y )
m a vvud, ' ( y ) 1 . U h ol d a
Teskari funksiyasi
5 5
(4.1.4) formulaga ko‗ra, g ( y ) f 2 y 1 1 f 2 y , y ( ; ) .
5
5 5
5
4.2- m i sol y o r d a mida taq s i m ot va z ichlik fun k s iya lar n i n g formulalarini tekshiramiz:
G ( y ) P { Y y } P { 5 X 2 y } P X 2 y
5
1 P X 2 y 1 P X 2 y P X 2 y
5
5
5
2 y .
1 P X 2 y 1 F
X
5
5
2 y
2 y '
Dem a k, G ( y ) 1 F X
'
g ( y ) G ( y ) 1 F
, u holda
X
5
5
y
2 y 1
2 y 2 y '
5 , ya ‘ n i
f
f X
5 5
5
y
g ( y ) 1 f 2 y , y ( ; ) .
5
5
Y = aX + b chiziqli almashtirish taqsimot xarakterini o‗zgartirmaydi: normal t.m.dan normal t.m.; tekis t.m.dan tekis t.m. hosil bo‗ladi.
4.3-misol. X t.m. , intervalda tekis taqsimlangan. Y cos X
2
2
t.m.ning matematik kutilmasini a) g ( y ) zichlik funksiyani topib; b) g ( y )
zichlik funksiyani topmasdan hisoblang.
1 , x ,
2
2
a) X t.m.ning zichlik funksiyasi
bo‗ladi.
x ,
f ( x )
2 2
0 , x ,
2
monoton
2
intervalda y cos x funksiya
e m a s : x , 0
intervalda
2
o‗suvchi, x 0 , intervalda esa kamayuvchi. Birinchi intervalda teskari
2
x 1 a r cc os y 1 ( y )
f u n k s iy a , i k k i n c hi i nter v a l d a e s a
x 2 arccos y 2 ( y ) ga teng. U holda (4.1.5) formulaga asosan

1 1
2
1
f ( ( y ) ) ( y )
( y ) ) ( y )
'
'
1
g ( y ) f (
1
2 2
1
1 y 2
1 y 2
1 y 2
De m a k,
2
, a g a r 0 y 1 ,
g ( y )
1 y 2
a g a r y 0 y ok i y 1.
o ,
U holda
1
2
dy
M Y y g ( y ) d y y
1 y 2
0
1 1
2
1
1
2
2
( 1 y 2 ) 2 d ( 1 y 2 ) 2 1 y 2 1
.
0
0
b) (4.1.6) formuladan foydalanamiz:
2
2
1
1
1
.
M Y c o s x d x sin x 2 ( 1 ( 1 ) )
2
2
4.2 Ikki argumentning funksiyalari
- Agar X va Y t.m.lar qabul qiladigan qiymatlarining har bir juftligiga biror qoidaga ko‗ra Z t.m. mos qo‗yilsa, u holda Z t.m. X va Y ikki tasodifiy argumentning funksiyasi deyiladi va Z ( X , Y ) kabi belgilanadi.
Z ( X , Y ) funksiyaning amaliyotda muhim ahamiyatga ega bo‗lgan xususiy holi Z X Y t.m.ning taqsimotini topamiz.
( X , Y ) ikki o‗lchovli uzluksiz t.m. f ( X , Y ) birgalikdagi zichlik
funksiyaga ega bo‗lsin. (3.4.3) formuladan foydalanib, Z X Y t.m.ning taqsimot funksiyasini topamiz:
F Z ( z ) P { Z z } P { X Y z } f ( x , y ) d x d y ,
D z
( 4 .2.1)
b u ye r d a D z { ( x , y ) : x y z } ( 3 1 -ras m ) .

D z
31 - ras m .
z x
U holda F Z ( z ) f ( x , y ) dy dx . Hosil bo‗lgan tenglikni z o‗zgaruvchi
bo‗yicha differensiallab, Z X Y t.m. uchun zichlik funksiyaga ega bo‗lamiz:
f Z ( z ) f ( x , z x ) d x .
( 4 .2.2)
Agar X va Y t. m .lar bo g ‗ li q s iz b o ‗ l s a , f ( x , y ) f ( x ) f ( y ) ten g l i k o ‗ r i n l i bo‗ladi va (4.2.2) formula
f Z ( z ) f X Y ( z ) f 1 ( x ) f 2 ( z x ) d x
( 4 .2.3)
ko‗rinishda bo‗ladi.
- B o g ‗ l i q s iz t.m . l a r y i g ‗ i nd i s ini n g taq s i m oti s h u t. m .l a r taqsimotlarining kompozitsiyasi deyiladi. Z t.m.ning zichlik funksiyasi
f X Y f X f Y
ko‗rinishda yoziladi, bu yerda * - kompozitsiya belgisi.
X uddi s h u nd a y a g a r Z Y X k o ‗ r i nish d a y o zi b o l s a k, u ch un boshqa formulaga ega bo‗lamiz:
f Z ( z )
f Z ( z ) f ( z y , y ) d y ,

agar X va Y t.m.lar bog‗liqsiz bo‗lsa, u holda
f Z ( z ) f 1 ( z y ) f 2 ( y ) d y .
t.m.larning taqsimotlarini topish ham xuddi shunga
Z X Y , Z X Y
o‗xshash amalga oshiriladi.
4.4- m i sol. Agar X va Y t. m .l a r b o g ‗ l i q s iz b o ‗ lib, X N ( 0 , 1 ) ,
Y N ( 0 , 1 )
asosan:
bo‗lsa, Z X Y ning taqsimotini toping. (4.2.3) formulaga
z 2
z 2
2 x
4
x 2
2
2
f Z ( z )
( z x ) 2
2 x 2 2 z x z 2
1
1
1
1
2
e
e
e
e
d x
d x
d x
2
2
2
2
2
2
z 2
2 2
2
- z 2
z 1
2 2
z 2
1
1
2
x z
2
e e
e e d x
,
4
4
2
2 2
z 2
1 2 2 2
ya‘ni f X Y ( z )
e
. Demak, bog‗liqsiz, normal taqsimlangan
2 2
t.m.lar ( a 0, 1 parametrli) yig‗indisi ham normal taqsimlangan ( a 0, 2 parametrli) bo‗lar ekan.
4.5-misol. X va Y t.m.larning birgalikdagi zichlik funksiyasi berilgan:
f ( x , y ) x y , a g a r 0 x 1 , 0 y 1 ,
0, aks holda.
Z X Y t.m.ning zichlik funksiyasini toping.
Avval Z t.m.ning taqsimot funksiyasi F Z ( z ) ni topamiz.
F Z ( z ) P { Z z } P { X Y z } ( x y ) d x d y ,
D z
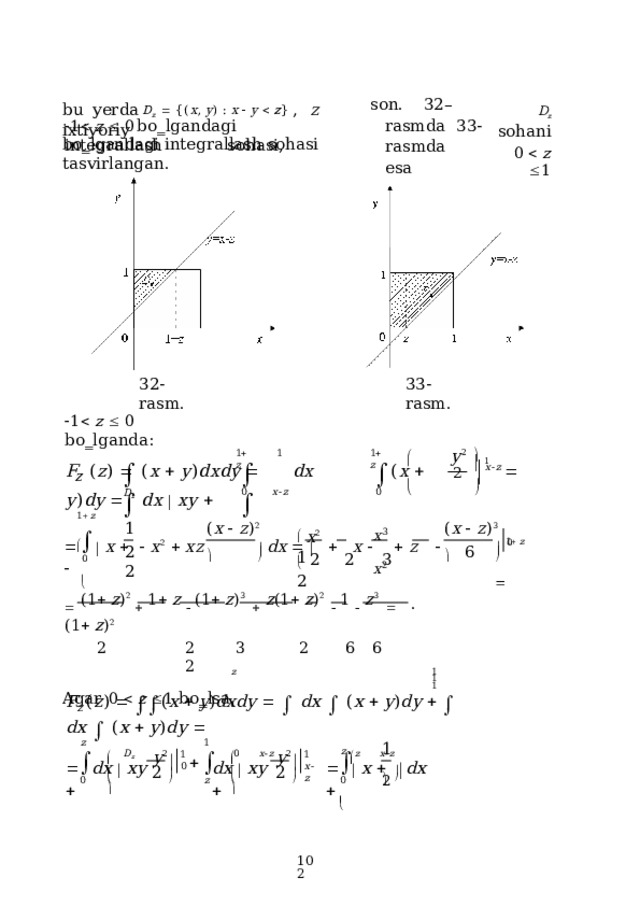
D z sohani
0 z 1
son. 32–rasmda 33 -ras m da e s a
bu yerda D z {( x , y ) : x y z } , z ixtiyoriy
1 z 0 b o ‗ l g a nd a gi i nt e grallash s oh a s i,
bo‗lgandagi integrallash sohasi tasvirlangan.
32-rasm.
33-rasm.
1 z 0 b o ‗ l g a nd a :
1 z
1 z
1
y 2 1
2 x z
F ( z ) ( x y ) d x d y d x ( x y ) d y d x x y
Z
0 x z
D z
0
1 z
x 3 x 2
( x z ) 3
( x z ) 2
x 2 1
1
1 z
dx x z
x x 2 x z
0
6
2 2
2 2 3 2
0
(1 z ) 2 1 z (1 z ) 3 z (1 z ) 2 1 z 3 (1 z ) 2
2 2 3 2 6 6 2
Agar 0 z 1 b o ‗ l s a ,
.
z 1 1 1
F Z ( z ) ( x y ) dxdy dx ( x y ) dy dx ( x y ) dy
D z 0 x z z x z
z
z
1
y 2
1
y 2
1
1
0
x d x
d x x y
- d x x y
2
x z
2
2
0
0
z
 1. Zichlik funksiyasi esa, a g a r z 1 , z 1 , 0 , ' agar -1F ( z ) f ( z ) z 1 , Z Z 1 z , a g a r 0 IV bobga doir misollar 1. X diskret t.m.ning taqsimot jadvali berilgan: X -2 p -1 0.10 0.20 0 1 0.30 0.25 2 3 0.10 0.05 a ) Y 2 X 2 3 ; b) X 2 ; c ) qonunlarini toping. Y sin X 3 t.m.larning taqsimot Y 2. Diskret X t.m.ning taqsimot qonuni X p -2 -1 0.2 0.1 0 1 0.3 2 0.1 0.3 b o ‗ l s a , Y X 2 1, t.m.larning taqsimot qonunlarini toping. Z X " width="640"
1. Zichlik funksiyasi esa, a g a r z 1 , z 1 , 0 , ' agar -1F ( z ) f ( z ) z 1 , Z Z 1 z , a g a r 0 IV bobga doir misollar 1. X diskret t.m.ning taqsimot jadvali berilgan: X -2 p -1 0.10 0.20 0 1 0.30 0.25 2 3 0.10 0.05 a ) Y 2 X 2 3 ; b) X 2 ; c ) qonunlarini toping. Y sin X 3 t.m.larning taqsimot Y 2. Diskret X t.m.ning taqsimot qonuni X p -2 -1 0.2 0.1 0 1 0.3 2 0.1 0.3 b o ‗ l s a , Y X 2 1, t.m.larning taqsimot qonunlarini toping. Z X " width="640"
1
1
x 2 x
( x z ) 2
x
x x 2 x z
dx
2 0
2
2
2
z
x 2
3
3
2
- x x z
2
z 2 z 1
x 2
( x z )
1
2
z
.
2 3
2
6
Yuqoridagi hisoblardan
0 ,
agar z 1,
agar -1
( 1 z ) 2
,
2
F ( z )
z
z 2 2 z 1
, a g a r 0
2
1, agar z1.
Zichlik funksiyasi esa,
a g a r z 1 , z 1 ,
0 ,
'
agar -1
F ( z ) f ( z ) z 1 ,
Z
Z
1 z , a g a r 0
IV bobga doir misollar
1. X diskret t.m.ning taqsimot jadvali berilgan:
X
-2
p
-1
0.10
0.20
0
1
0.30
0.25
2
3
0.10
0.05
a ) Y 2 X 2 3 ; b) X 2 ; c ) qonunlarini toping.
Y sin X
3
t.m.larning taqsimot
Y
2. Diskret X t.m.ning taqsimot qonuni
X
p
-2
-1
0.2
0.1
0
1
0.3
2
0.1
0.3
b o ‗ l s a , Y X 2 1,
t.m.larning taqsimot qonunlarini toping.
Z X
![3 . Agar X R [ 2 , 2 ] b o ‗ l s a , Y X 1 t.m . ning z ichl i k f u n k s iy a s i va dispersiyasini toping. Agar X N ( 0 , 1 ) b o ‗ l s a , a ) Y 3 X 3 ; b) Y X funksiyasini toping. X R(0,2) vа Y=-3X+1 bo‗lsa, Y t.m.ning taqsimot funksiyasini toping. Taqsimoti t.m.larning zichlik Х Р -1 0.4 0 0.1 1 0.5 b o ‗ l g a n t. m .dan t u z ilg a n У = 2 X t. m .ning m a t e m a tik kut i l m a s i va dispersiyasini toping. Таqsimoti Р(Х=-1)=P(X=1)=1/2 bo‗lgan t.m.dan olingan Z 1 =cosX , Z 2 =sinX t.m.larning matematik kutilmalari va dispersiyalarini toping. Таqsimoti b o ‗ l g a n t. m .dan t u z ilg a n У = Х t. m . ni n g matematik kutilmasi va dispersiyasini toping. Х Р -1 0 0.2 0.3 1 0.3 2 0.2 Y : 1 , 1 9. X Bi(2,1/3); vа X Y bo‗lsa, Z=X+2Y t.m.ning P : 1 / 4 , 3 / 4 matematik kutilmasi va dispersiyasini toping. 10. Ikkita tanga va kub tashlash tajribasida ―gerb‖lar soni Х va kubdagi ochkolar soni У ning birgalikdagi taqsimot jadvalini tuzing va DХ, DУ larni hisoblang. berilgan 11. X uzluksiz t.m.ning zichlik funksiyasi b o ‗ lsin : t.m.larning Y X 2 zichlik e x , a g a r x 0 , a ) Y 2 X 1 ; b) f ( x ) 0, agar x 0. funksiyalarini toping. 12 . Agar X R [ 0 , 4 ] , Y zichlik funksiyasini toping. R [0,1] va X Y bo‗lsa, Z X Y t.m.ning 13. Bog‗liqsiz X va Y t.m.larning taqsimot qonunlari berilgan Y p -1 0.2 0 0.25 1 0.3 2 0.25 X -1 p 0.4 1 0.3 2 0.3 bo‗lsa, X+Y va XY t.m.larning taqsimot qonunlarini toping.](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img103.jpg)
3 . Agar X R [ 2 , 2 ] b o ‗ l s a , Y X 1 t.m . ning z ichl i k f u n k s iy a s i va dispersiyasini toping.
- Agar X N ( 0 , 1 ) b o ‗ l s a , a ) Y 3 X 3 ; b) Y X
funksiyasini toping.
- X R(0,2) vа Y=-3X+1 bo‗lsa, Y t.m.ning taqsimot funksiyasini toping.
- Taqsimoti
t.m.larning zichlik
Х
Р
-1
0.4
0
0.1
1
0.5
b o ‗ l g a n t. m .dan t u z ilg a n У = 2 X t. m .ning m a t e m a tik kut i l m a s i va dispersiyasini toping.
- Таqsimoti Р(Х=-1)=P(X=1)=1/2 bo‗lgan t.m.dan olingan Z 1 =cosX , Z 2 =sinX t.m.larning matematik kutilmalari va dispersiyalarini toping.
- Таqsimoti
b o ‗ l g a n t. m .dan t u z ilg a n У = Х t. m . ni n g matematik kutilmasi va dispersiyasini toping.
Х
Р
-1
0
0.2
0.3
1
0.3
2
0.2
Y : 1 , 1
9. X Bi(2,1/3);
vа X Y bo‗lsa, Z=X+2Y t.m.ning
P : 1 / 4 , 3 / 4
matematik kutilmasi va dispersiyasini toping.
10. Ikkita tanga va kub tashlash tajribasida ―gerb‖lar soni Х va kubdagi ochkolar soni У ning birgalikdagi taqsimot jadvalini tuzing va DХ, DУ larni hisoblang.
berilgan
11. X uzluksiz t.m.ning zichlik funksiyasi
b o ‗ lsin :
t.m.larning
Y X 2
zichlik
e x , a g a r x 0 ,
a ) Y 2 X 1 ; b)
f ( x )
0, agar x 0.
funksiyalarini toping.
12 . Agar X R [ 0 , 4 ] , Y
zichlik funksiyasini toping.
R [0,1] va X Y bo‗lsa, Z X Y t.m.ning
13. Bog‗liqsiz X va Y t.m.larning taqsimot qonunlari berilgan
Y
p
-1
0.2
0
0.25
1
0.3
2
0.25
X
-1
p
0.4
1
0.3
2
0.3
bo‗lsa, X+Y va XY t.m.larning taqsimot qonunlarini toping.
![V bob. Ehtimollar nazariyasining limit teoremalari Ehtimollar nazariyasining limit teoremalari deb nomlanuvchi qator tasdiq va teoremalarni keltiramiz. Ular yetarlicha katta sondagi tajribalarda t.m.lar orasidagi bog‗lanishni ifodalaydi. Limit teoremalar shartli ravishda ikki guruhga bo‗linadi. Birinchi guruh teoremalar katta sonlar qonunlari(KSQ) deb nomlanadi. Ular o‗rta qiymatning turg‗unligini ifodalaydi: yetarlicha katta sondagi tajribalarda t.m.larning o‗rta qiymati tasodifiyligini yo‗qotadi. Ikkinchi guruh teoremalar markaziy limit teoremalar(MLT) deb nomlanadi. Yetarlicha katta sondagi tajribalarda t.m.lar yig‗indisining taqsimoti normal taqsimotga intilishi shartini ifodalaydi. KSQ ni keltirishdan avval yordamchi tengliklarni isbotlaymiz. 5.1 Chebishev tengsizligi Teorema(Chebishev). Agar X t.m. DX dispersiyaga ega bo‗lsa, u holda 0 uchun quyidagi tengsizlik o‗rinli: P X M X D X . ( 5 .1.1) 2 (5.1.1) tengsizlik Chebishev tengsizligi deyiladi. P X a Isboti. e hti m ollik X t . m .ning [ a ; a ] orali q qa tushmasligi ehtimolligini bildiradi bu yerda a MX . U holda a P X a d F ( x ) d F ( x ) a x a d F ( x ) ( x a ) 2 x a 2 x a d F ( x ) , 1 d F ( x ) ( x a ) 2 2 c hun k i x a i n teg r a ll a s h s oh a s i ni k o ‗ ri nish d a y o z i sh ( x a ) 2 mumkin. Bu yerdan 1 ekanligi kelib chiqadi. Agar integrallash 2 sohasi kengaytirilsa, musbat funksiyaning integrali faqat kattalashishini hisobga olsak,](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img104.jpg)
V bob. Ehtimollar nazariyasining limit teoremalari
Ehtimollar nazariyasining limit teoremalari deb nomlanuvchi qator tasdiq va teoremalarni keltiramiz. Ular yetarlicha katta sondagi tajribalarda t.m.lar orasidagi bog‗lanishni ifodalaydi. Limit teoremalar shartli ravishda ikki guruhga bo‗linadi. Birinchi guruh teoremalar katta sonlar qonunlari(KSQ) deb nomlanadi. Ular o‗rta qiymatning turg‗unligini ifodalaydi: yetarlicha katta sondagi tajribalarda t.m.larning o‗rta qiymati tasodifiyligini yo‗qotadi. Ikkinchi guruh teoremalar markaziy limit teoremalar(MLT) deb nomlanadi. Yetarlicha katta sondagi tajribalarda t.m.lar yig‗indisining taqsimoti normal taqsimotga intilishi shartini ifodalaydi. KSQ ni keltirishdan avval yordamchi tengliklarni isbotlaymiz.
5.1 Chebishev tengsizligi
Teorema(Chebishev). Agar X t.m. DX dispersiyaga ega bo‗lsa, u holda 0 uchun quyidagi tengsizlik o‗rinli:
P X M X D X .
( 5 .1.1)
2
(5.1.1) tengsizlik Chebishev tengsizligi deyiladi.
P X a
Isboti.
e hti m ollik X t . m .ning [ a ; a ] orali q qa
tushmasligi ehtimolligini bildiradi bu yerda a MX . U holda
a
P X a d F ( x ) d F ( x )
a
x a
d F ( x )
( x a ) 2
x a
2
x a
d F ( x ) ,
1 d F ( x )
( x a ) 2 2
c hun k i x a i n teg r a ll a s h s oh a s i ni k o ‗ ri nish d a y o z i sh
( x a ) 2
mumkin. Bu yerdan
1 ekanligi kelib chiqadi. Agar integrallash
2
sohasi kengaytirilsa, musbat funksiyaning integrali faqat kattalashishini hisobga olsak,

1
1
1
2
x a
P X a
2
( x a ) 2 dF ( x ) DX .
( x a ) 2 d F ( x )
■
2
Chebishev tengsizligini quyidagi ko‗rinishda ham yozish mumkin:
P X M X 1 D X .
( 5 .1.2)
2
Chebishev tengsizligi ihtiyoriy t.m.lar uchun o‗rinli. Xususan, X t.m.
taqsimlangan
b o ‗ lsin , h o l d a
q 1 p (0,1) . U
binomial qonun bo‗yicha
P { X m } C m p m q n m , m 0 , 1 , ..., n ,
n
MX a np , DX npq va (5.1.1) dan
P m n p 1 np q ;
( 5 .1.3)
2
p M m a ,
dispersiyasi
n ta bog‗liqsiz tajribalarda ehtimolligi
n
D m qp b o ‗ l g a n h od i s a n i ng m c h a s t o tasi u c h u n,
n
n n
P m p 1 q p .
( 5 .1. 4 )
n
n 2
X t.m.ni [ ; ) oraliqga tushushi ehtimolligini baholashni Markov tengsizligi beradi.
Teorema(Markov). Manfiy bo‗lmagan, matematik kutilmasi MX
c h e kli b o ‗ l g a n X t.m. uch u n 0 da
P X MX
( 5 .1.5)
tengsizlik o‗rinli.
Isboti. Quyidagi munosabatlar o‗rinlidir:
x 1
MX
P X d F ( x ) d F ( x ) x d F ( x )
. ■
0
(5.1.5) tengsizlikdan (5.1.1) ni osongina keltirib chiqarish mumkin. (5.1.5) tengsizlikni quyidagi ko‗rinishda ham yozish mumkin:
P X 1 M X .
( 5 .1.6)
5.1.-misol. X diskret t.m.ning taqsimot qonuni berilgan:
X : 1 2 3
0.4
X M X
P
Chebishev tengsizligidan foydalanib,
P :0.3 0.2 0.5.
X
ehtimollikni baholaymiz. X t.m.ning sonli xarakteristikalarini hisoblaymiz:
MX 1 0.3 2 0.2 3 0.5 2.2 ; DX 1 2 0.3 2 2 0.2 3 2 0.5 2.2 2 0.76 .
0 . 4 1 0 . 7 6 0 . 9.
Chebishev tengsizligiga ko‗ra: P X 2.2
0 . 4
5.2 Katta sonlar qonuni Chebishev va Bernulli teoremalari
Ehtimollar nazariyasi va uning tadbiqlarida ko‗pincha yetarlicha katta sondagi t.m.lar yig‗indisi bilan ish ko‗rishga to‗g‗ri keladi. Yig‗indidagi har bir t.m.ning tajriba natijasida qanday qiymatni qabul qilishini oldindan aytib bo‗lmaydi. Shuning uchun katta sondagi t.m.lar yig‗indisining taqsimot qonunini hisoblash burmuncha qiyinchilik tug‗diradi. Lekin ma‘lum shartlar ostida yetarlicha katta sondagi t.m.lar yig‗indisi tasodifiylik xarakterini yo‗qotib borar ekan. Amaliyotda juda ko‗p tasodifiy sabablarning birgalikdagi ta‘siri tasodifga deyarli bog‗liq bo‗lmaydigan natijaga olib keladigan shartlarni bilish juda muhimdir. Bu shartlar ―Katta sonlar qonuni‖ deb ataluvchi teoremalarda keltiriladi. Bular qatoriga Chebishev va Bernulli teoremalari kiradi.
- X 1 , X 2 , .. . X n , ...
t.m.lar o‗zgarmas son A ga ehtimollik bo‗yicha
ya qi n las h a di d ey il a di, a g a r 0 u c hun
l i m P X n A 1
n
P
munosabat o‗rinli bo‗lsa. Ehtimollik bo‗yicha yaqinlashish X n A kabi
n
belgilanadi.
- X 1 , X 2 , .. . X n , ...
t.m . lar ket m a-k e tli g i m o s ravish d a
MX 1 , MX 2 ,... MX n ,... matematik kutilmalarga ega bo‗lib, 0 son uchun
n da
1
n
n
i i
M X 1
lim P 1 X
n i 1
n i 1
n
X 1 , X 2 , .. . X n
munosabat bajarilsa, t.m.lar ketma-ketligi katta sonlar
qoniniga bo‘ysunadi deyiladi.
Teorema(Chebishev). Agar bog‗liqsiz X 1 , X 2 ,... X n ,... t.m.lar ketma-
k e tligi u ch un s h u n d a y C 0 b o ‗ l i b ten g s izli k l a r o‗rinli bo‗lsa, u holda 0 uchun
D X i C , i 1 , 2 , . . .
1
n
n
i i
M X 1
lim P 1 X
(5.2.1)
n i 1 n i 1
n
munosabat o‗rinli bo‗ladi.
Is b ot i . D X i C , i 1 , 2 , . . . b o ‗ l g a ni u c hun
1
1 1
1
1
n
n
n
i i
X D
X
D
C .. . C
D X .. . D X
DX
2 2
1 n
i
2
2
n
n
n n n
i 1 i 1
i 1
1 Cn C . U holda Chebishev tengsizligiga ko‗ra:
n 2
n
D 1 n X
n i
C
n 2
1
1
n
n
P X M X
i 1
1
1
.
(5.2.2)
2
i
i
n
n
i 1 i 1
1
n
n
M X 1
X
l i m P 1
. ■
E ndi n da l i m itga o ‗ ts a k,
i
i
n i 1 n i 1
n
X 1 , X 2 , .. . X n , ...
Na ti j a. Agar
bog‗liqsiz va bir xil taqsimlangan
M X i a , D X i
2
t.m.lar va
bo‗lsa, u holda 0 uchun quyidagi
munosabat o‗rinli
n
i
l i m P 1 X a 1
.
( 5 .2.3)
n i 1
n
Bernulli teoremasi katta sonlar qonuninig sodda shakli hisoblanadi.
U nisbiy chastotaning turg‗unligini asoslaydi.
Teorema(Bernulli). Agar A hodisaning bitta tajribada ro‗y berishi
ehtimolligi p bo‗lib, n ta bog‗liqsiz tajribada bu hodisa marta ro‗y bersa, u holda 0 uchun
n A
n
p 1
l i m P
A
( 5 .2.4)
n
n
munosabat o‗rinli.
Is b ot i . X 1 , X 2 , .. . X n
indikator t.m.larni quyidagicha kiritamiz: agar i -
tajribada A hodisa ro‗y bersa, X i 1 ; agar ro‗y bermasa X i 0 . U holda
n
n A X i . X i
i 1
ni quyidagi ko‗rinishda yozish mumkin:
t. m .ning
n A
X i : 0 1
X
taqsimot qonuni ixtiyoriy i da: P :1 p p bo‗ladi. i t.m.ning matematik
M X i 1 p 0 ( 1 p ) p
g a , d i s p e rsi y a s i t. m . l a r b o g ‗ l i q s iz va
ku t il m a s i
X i
p ( 1 p ) p q .
D X i ( 0 p ) ( 1 p ) ( 1 p ) p
2 2
1 2
1
4
1
p .
p ( 1 p ) p p 2
ularning dispersiyalari chegaralangan,
2 4
1
n
n
i i
M X 1
lim P 1 X
U holda Chebishev teoremasiga asosan:
n i 1
n i 1
n
n
1
1
n
n
i
i
p 1
l i m P
A
X n A
MX 1 np
.
p bo‗lgani uchun
va
;
n
n
n
n i 1
n i 1
n
■
5.3 Markaziy limit teorema
Markaziy limit teorema t.m.lar yig‗indisi taqsimoti va uning limiti – normal taqsimot orasidagi bog‗lanishni ifodalaydi. Bir xil taqsimlangan t.m.lar uchun markaziy limit teoremani keltiramiz.
Teorema. X 1 , X 2 ,... X n bog‗liqsiz, bir xil taqsimlangan, MX i a
chekli matematik kutilma va DX i , i 1, n dispersiyaga ega bo‗lsin,
2
![X n n n i i X M X na i i 1 i 1 Z i 1 0 u holda t.m.ning taqsimot 2 n n X n D i i 1 qonuni n da standart normal taqsimotga intiladi 1 2 x t 2 e 2 dt . F ( x ) P { Z x } ( x ) ( 5 .3.1) Z n n n Z n N ( 0 , 1 ) , bo‗yicha De m a k, ( 5 .3.1) ga k o ‗ ra ye tarl i c ha k a tta n lar d a y i g ‗ i ndi e s a qu y i d ag i n or m a l q o n u n S n X 1 X n n n ) . Bu holda X i t.m. asimptotik i 1 taqsimlangan bo‗ladi: S n N ( na , normal taqsimlangan deyiladi. Agar X t.m. uchun MX 0, DX 1 bo‗lsa X t.m. markazlashtirilgan va normallashtirilgan(yoki standart) t.m. deyiladi. (5.3.1) formula yordamida b il a n b o g‗ l i q h o d i s a lar t.m.ni standartlashtirsak, yetarlicha katta n larda t.m.lar yig‗indisi S n X i i 1 e hti m olli g i ni h iso b lash m u m ki n . yetarlicha katta n larda n n a n X i n a n a n a n a n P X P i 1 , n n i n n n i 1 y oki M S n M S n . P S ( 5 .3.2) n D S D S n n 5.2-misol. b o ‗ l s a , Y X i X i bog‗liqsiz t.m.lar [0,1] oraliqda tekis taqsimlangan 100 P { 5 5 Y 7 0 } t.m.ning taqsimot qonunini toping va i 1 ehtimollikni hisoblang.](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img109.jpg)
X
n
n
n
i
i
X M
X na
i
i 1 i 1
Z
i 1
0 u holda
t.m.ning taqsimot
2
n
n
X
n
D
i
i 1
qonuni n da standart normal taqsimotga intiladi
1
2
x
t 2
e 2 dt .
F ( x ) P { Z x } ( x )
( 5 .3.1)
Z n
n
n
Z n N ( 0 , 1 ) ,
bo‗yicha
De m a k, ( 5 .3.1) ga k o ‗ ra ye tarl i c ha k a tta n lar d a
y i g ‗ i ndi e s a qu y i d ag i n or m a l q o n u n
S n X 1 X n
n
n ) . Bu holda X i t.m. asimptotik
i 1
taqsimlangan bo‗ladi: S n N ( na ,
normal taqsimlangan deyiladi.
Agar X t.m. uchun MX 0, DX 1 bo‗lsa X t.m. markazlashtirilgan va
normallashtirilgan(yoki standart) t.m. deyiladi. (5.3.1) formula yordamida
b il a n b o g‗ l i q h o d i s a lar t.m.ni standartlashtirsak,
yetarlicha katta n larda t.m.lar yig‗indisi
S n X i
i 1
e hti m olli g i ni h iso b lash m u m ki n . yetarlicha katta n larda
n
n a
n
X i n a
n a
n a
n a
n
P X P
i 1
,
n
n
i
n
n
n
i 1
y oki
M S n M S n .
P S
( 5 .3.2)
n
D S D S
n n
5.2-misol.
b o ‗ l s a , Y X i
X i
bog‗liqsiz t.m.lar [0,1] oraliqda tekis taqsimlangan
100
P { 5 5 Y 7 0 }
t.m.ning taqsimot qonunini toping va
i 1
ehtimollikni hisoblang.

Markaziy limit teorema shartlari bajarilganligi uchun, Y t.m.ning
( y M Y ) 2
1
2 2
bo‗ladi. Tekis taqsimot matematik
zichlik funksiyasi
e
f ( y )
y
Y
2 y
0 1 1 (1 0) 2 1
, DX i
2 2
1 2 1 2
kutilmasi va dispersiyasi formulasidan MX i
10 0
1
10 0
MY M
X M X 10 0 5 0 ,
bo‗ladi. U holda
i
i
2
i 1 i 1
10 0
5 3
1 2 5
10 0
i i
X D X 10 0 ,
DY D
, s h u ning uc hun,
Y
3
1 2 3
i 1 i 1
3 ( y 5 0 ) 2
3
f Y ( y )
e
50
. (5.3.2) formulaga ko‗ra,
5 6
4 3 3 0.04.
70 50 55 50
P 55 S n 7 0
5 3 5 3
3 3
V bobga doir misollar
1 . B o g ‗ l i q s iz bir x i l taq s i m lan g a n ketligining taqsimot qonuni berilgan
k e t m a-
t. m . l a r
X 1 , X 2 , . .. , X n , . . .
X n
P
a
n
- a
n 1
2 n 1
2 n 1
Bu ketma-ketlik K.S.Q. bo‗ysunadimi?
2. Bog‗liqsiz bir xil taqsimlangan
ketligining taqsimot qonuni berilgan
t. m . l a r
k e tma-
X 1 , X 2 , . .. , X n , . . .
X
P
n
n
1 / 2 n
0
n
1 1
1 / 2 n
2 n
Bu ketma-ketlik K.S.Q. bo‗ysunadimi?
3. Diskret t.m. taqsimot qonuni berilgan:
X
0.1
P
0.4
0.2
0.3
0.6
0.5

Chebishev tengsizligidan foydalanib
X MX 0.4 ni baholang.
4. X 1 , X 2 ,..., X n ,... bog‗liqsiz t.m.lar ketma-ketligi quyidagi taqsimotga
2 n 2 ( 2 n 1 ) ,
P X
P X 0 1 2 2 n . B u t. m .l a r u c hun
ega bo‗lsin:
n
n
K.S.Q. o‗rinlimi?
- Detalning nostandart bo‗lish ehtimolligi 0.2 ga teng. 400 ta detaldan iborat partiyada nostandart detal chiqishning chastotasi va ehtimoli orasidagi farqning moduli 0.05 dan kichik bo‗lishini ehtimolligini baholang.
- Chebishev tengsizligidan foydalanib, quyidagi ehtimollikni baholang:
simmetrik tanga 500 marta tashlanganda gerb tushushlari soni k uchun
20 0 k 30 0 o ‗ r i n l i.
Ikkinchi bo‘lim MATEMATIK STATISTIKA
VI bob. Tanlanma va uning xarakteristikalari
6.1 Matematik statistika predmeti
Oldingi bo`limlardan ma`lumki, ehtimollar nazariyasi tasodifiy hodisalar bilan bog`liq jarayonlarning matemetik modellarini o`rganish bilan shug`ullanadi. Ixtiyoriy tasodifiy jarayonlarga mos matematik modellar yordamida bizni qiziqtirayotgan u yoki bu hodisalarning ro`y berish ehtimolligini topishimiz mumkin.
Matematik statistika tasodifiy hodisalar yoki jarayonlar haqida shu hodisalarni kuzatish yoki tajribalar natijasida olingan ma‘lumotlar asosida umumiy xulosalar chiqaradigan matematik fandir. Bu xulosalar umumiylik xususiyatlariga ega bo‗lib, kuzatilayotgan tasodifiy holatlarning barchasiga taaluqlidir. Matematik statistika ehtimollar nazariyasiga tayangan holda, uning usullari va nazariy hulosalari asosida o‗rganilayotgan obyekt haqida xulosalar chiqaradi. Agarda ehtimollar nazariyasida biz o‗rganayotgan matematik model to‗la-to‗kis berilgan deb hisoblab, bu model bizni qiziqtirayotgan holatlarni o‗rgansak, matematik statistikada biz qandaydir tasodifiy hodisalar natijalaridan kelib chiqqan holda(bular ko‗pchilik hollarda sonlardan iborat bo‗ladi), tasodifiy jarayonlarning matematik modelini tuzishga harakat qilamiz. Matematik statistika o‗zining xulosa chiqarish usullari yordamida o‗rganilayotgan obyektning nazariy ehtimoliy modelini tuzishga qaratilgan. Masalan, Bernulli sxemasida biz kuzatayotgan A hodisaning bitta tajribada ro‗y berish ehtimolligi p bo‗lsin. Bizni n ta bog‗liqsiz tajribalar natijasida A hodisasining k ( k n ) marta ro‗y berish ehtimolligi qiziqtirsin. Bu masala ehtimollar nazariyasining usullari bilan to‗liq hal etiladi. Endi shunday masala qo‗yilsin: n ta bog‗liqsiz tajribalarda bizni qiziqtiradigan A hodisa k marta ro‗y bersin. U holda shu hodisaning bitta tajribada ro‗y berish ehtimolligi p deb qanday miqdorni olish kerak? Bu hol matematik statistikaning namunaviy masalasidir. Ko‗rinib turibdiki, matematik statistika masalalari ehtimollar nazariyasi masalalariga teskari masalalar ekan.
Matematik statistika o‗z hulosalarida biz qiziqayotgan tasodifiy hodisalarni tavsiflaydigan, odatda sonlardan iborat bo‗lgan statistic ma‘lumotlar asosida o‗rganilayotgan tasodifiy jarayonning nazariy-
ehtimoliy qonuniyatlarini tuzish uchun turli usullarni ishlab chiqishga qaratilgandir.
Endi Bernulli sxemasi misolida matematik statistika
shug‗ullanadigan va hal qilinadigan asosiy masalalarni ko‗rib chiqaylik.
I. Noma’lum parametrni statistik baholash. n ta tajriba natijasida biz kuzatayotgan A hodisa m marta ro‗y bersin. U holda, shu ma‘lumotlar
asosida biz shunday p € miqdorni aniqlaylikki, uni p P ( A ) sifatida qabul
p € m
qilish mumkin bo‗lsin. Bizning holimizda A hodisaning chastotasini
n
deb qabul qilishimiz tabiiy. Albatta, biz statistik baho deb taklif etayotgan
p € miqdor ma‘lum ma‘noda noma‘lum parametr p ga yaqin bo‗lishi kerak.
II.Ishonchlilik oralig‘i. Ba‘zi hollarda noma‘lum parametr p ning aniq qiymati emas, balki 1 ga yetarlicha yaqin ehtimollik bilan uning
[ p € 1 ; p € 2 ]
qiy m a tini stati s t ik m a ‘ l u m otl a r a sosi d a a n i qlanad i g a n bi r or
oraliqqa tegishli bo‗lishi qiziqtiradi. Bunda oraliq chegaralari p € 1 va p € 2 - t.m.lar faqat m ga bog‗liq bo‗ladi. Tajriba natijasida to‗liq aniqlanadigan [ p € 1 ; p € 2 ] oraliq - i s h on c h l il i k o r a l i g ‗ i d ey il a di.
III. Statistik gipotezalarni tekshirish. Faraz qilatlik, qandaydir (aprior) mulohazalar asosida p p 0 degan xulosaga keldik. Bu yerda p 0 -
m n
a s o s i d a biz s tat i s t i k gipot ez a ning
aniq miqdor. Nisbiy chastota
p p
0
to‗g‗ri yoki noto‗g‗riligini tekshirishimiz kerak. Yetarli katta n lar uchun
m
nisbiy chastota p ehtimollikka yaqin bo‗lgani uchun, statistik gipoteza
n
m p ayirma asosida quriladi. Agarda bu
p p ni tekshiruvchi alomat
0
0
n
ayirma katta bo‗lsa, asosiy gipoteza rad etiladi, agarda bu ayirma
p p 0
yetarlicha kichik bo‗lsa, statistik gipotezani rad etishga asos bo‗lmaydi.
Yuqorida ko‗rsatilgan va boshqa statistik ma‘lumotlarni hal etish matematik statistikaning vazifasidir. Matematik statistika bu masalalarni o‗zining tushunchalari va statistik usullari bilan hal etadi.
6.2 Bosh va tanlanma to‘plam
Aytaylik, ishlab chiqarilgan mahsulotlarning katta to‗piga tegishli biron-bir xususiyat (masalan, mahsulotning o‗lchami, og‗irligi, narxi va hokazo) o‗rganilayotgan bo‗lsin. To‗pga tegishli barcha mahsulotlar bosh to‘plamni tashkil qiladi deyiladi. Ko‗p hollarda , bosh to‗plamga
mahsulotlar juda ko‗p miqdorda bo‗lib, ularning barchasini uzluksiz o‗lchash amaliyotda mumkin bo‗lmaydi. Ba‘zi hollarda bu umuman mumkin bo‗lmasa, ayrim hollarda juda katta xarajatlarni talab qiladi. Bunday hollarda bosh to‗plamdan tasodifiy ravishda chekli sondagi mahsulot ajratib olinadi va ularning xususiyatlari o‗rganiladi. Bu jarayon tanlanmalarga olib keladi. Demak, tanlanma bosh to‗plamdan tasodifiy ravishda olingan elementlar. Tanlanmalar usuli deganda biz bosh to‗plamdan tasodifiy ravishda olingan elementlarga xos bo‗lgan qaralayotgan xususiyatlarni statistik tahlil qilib, shular asosida bosh to‗plam elementlariga xos bo‗lgan xususiyatlar haqida umumiy xulosalar chiqarishni tushunamiz.
Matematik statistikada har qanday mulohaza va xulosalar statistik ma‘lumotlarga yoki boshqacha qilib aytganda tajriba natijalariga tayanadi.
Odatda tajriba natijalari taqsimoti F ( x ) bo‗lgan X t.m.ning
X 1 , X 2 , ... , X n
kuzatilmalaridan iborat bo‗ladi. Demak, kuzatilmalar bog‗liqsiz va X t.m. bilan bir xil taqsimlangan t.m.lar ekan.
- Kuzatilmalardan tuzilgan ( X 1 , X 2 ,..., X n ) vektor hajmi n ga teng
bo‗lgan t anlanma deyiladi.
Endi X bilan X t.m. qabul qiladigan qiymatlar to‗plami bo‗lsin. X
to‗plam bosh to‗plamdan iborat bo‗ladi. X to‗plam chekli yoki cheksiz bo‗lishi mumkin. Mavzu boshida ko‘rilgan misoldagi barcha mahsulotlarning xususiyatlaridan iborat to‗plam-bosh to‗plam va shu xususiyatlarning sonli ifodasi esa X t.m. qiymatlaridan iborat bo‗ladi. Bosh to‗plam X dan qiymatlar qabul qiluvchi X t.m.ning taqsimot funksiyasini va sonli xarakteristikalarini (masalan, matematik kutilma, dispersiya, yuqori tartibli momentlar va hokazo) mos ravishda nazariy taqsimot va nazariy sonli xarakteristikalar deyiladi. Kuzatishlar asosida aniqlangan taqsimot funksiya va unga mos sonli xarakteristikalar empirik yoki tanlanma taqsimot funksiyasi va sonli xarakteristikalari deyiladi.
6.3 Empirik taqsimot funksiya
Faraz qilaylik, taqsimot funksiyasi F ( x ) bo‗lgan X t.m. kuzatilayotgan bo‗lsin. ( X 1 , X 2 ,..., X n ) – vektor esa unga mos hajmi n ga teng bo‗lgan tanlanma bo‗lsin. Shu vektorning biron-bir aniq qiymati:
x ( x 1 , x 2 , ..., x n )
( 6 .3.1)

X t.m.ning amalga oshgan qiymati deyiladi. Har qanday tajriba natijalari (6.3.1) qatordan iborat bo‗lgan sonlar to‗plami bo‗ladi.
- Birinchi satri tajriba nomerlari, ikkinchisi esa X ning mos amaldagi
qiymatlaridan iborat bo‗lgan quyidagi jadvalga
1
2
x 1
x 2
3
…
x 3
n
…
x n
statistik qator deb ataladi. Statistik qator turli maqsadlarda va turli usullar bilan tahlil qilinishi mumkin. Mana shunday tahlilning maqsadi X t.m.ning empirik(yoki statistik) taqsimot funksiyasini tuzishdan iborat bo‗lishi mumkin.
(6.3.1) qatorni kamaymasligi bo‗yicha tartiblaymiz:
x ( 1 ) x ( 2 ) ... x ( n )
( 6 .3.2)
hosil bo‗lgan (6.3.2) qator variatsion qator deyiladi.
Ixtiyoriy statistik qator (6.3.1) yordamida empirik yoki tanlanma taqsimot funksiyasi aniqlanishi mumkin.
- Quyidagicha
n
i 1
F € ( x ) 1 I ( X x )
( 6 .3.3)
n
i
n
aniqlangan funksiya empirik (yoki tanlanma) taqsimot funksiyasi deyiladi. Bu yerda I ( A ) orqali A hodisa indikatori belgilangan. Statistik qator (6.3.1) t.m.lardan iborat bo‗lgani uchun, empirik taqsimot funksiya ham har bir tayinlangan x da t.m. bo‗ladi.
6.1-misol. Uzoqlikni o‗lchovchi asbob bilan ma‘lum masofa o‗lchanganda tasodifiy xatolikka yo‗l qo‗yildi. Tajriba 20 marta takrorlanganda yo‗l qo‗yilgan xatoliklar statistik taqsimot funksiyasini tuzing. Statistik qator quyidagicha bo‗lsin:
i
x i
1
2
5
-8
3
4
10
5
15
3
6
7
-6
8
-15
9
20
10
12
15
i
x i
11
12
-4
-2
13
14
20
15
14
-8
16
17
-12
18
16
19
10
20
-5
18

E ng kic h ik k u za ti l ma -15. De m a k, F € ( 1 5 ) 0 . - 15 bir m a r t a
20
kuzatildi, demak, uning chastotasi 1 . Shuning uchiun, -15 nuqtada
20
empirik taqsimot funksiya 1 ga teng bo‗lgan sakrashga ega, -15 nuqtadan
20
-12 nuqtagacha bo‗lgan oraliqda F € ( x ) funksiya 1 ga teng. -12 niqtada
n
20
empirik taqsimot funksiya 1 ga teng bo‗lgan sakrashga ega, -12 nuqtadan
20
2
20
ga teng. -8 niqtada
-8 nuqtagacha bo‗lgan oraliqda F € ( x ) funksiya
n
2
20
empirik taqsimot funksiya
ga teng bo‗lgan sakrashga ega, chunki -8
qiymat ikki marta uchraydi va hokazo. Empirik taqsimot funksiya grafigini chizamiz.
34-rasm.
Har qanday t.m.ning empirik taqsimot funksiyasi kuzatilgan nuqtalarda shu kuzatilmaning chastotasiga teng va sakrashga ega bo‗lgan pog‗onali, uzlukli funksiyadan iborat bo‗ladi.
Bernulli teoremasiga asosan tajribalar soni n cheksiz o‗sganda
{ X x } hodisaning chastotasi shu hodisaning ehtimolligiga intiladi. Bu esa empirik taqsimot funksiyaning n cheksizlikka intilganda haqiqiy
F ( x ) P { X x }
taq si m ot f u n k s iya ga i s ta l g a n c ha ya qin b o ‗ l i s h i ni anglatadi.
Empirik taqsimot haqida quyidagi tasdiqni keltirish mumkin.
![Teorema(Glivenko-Kantelli). Ixtiyoriy 0 uchun quyidagi munosabat o‗rinli € 1 . l im P s u p F ( x ) F ( x ) n n x Demak n ortgani sari F € ( x ) funksiya F ( x ) ga barcha x larda 1 n ehtimollik bilan tekis yaqinlashar ekan. 6.4 Gistogramma va poligon Tajribalar soni katta bo‗lsa, tajriba natijalari statistik qatori ham katta bo‗ladi. Shuning uchun, ko‗p hollarda intervallik statistik qatordan foydalanish maqsadga muvofiq bo‗ladi. Faraz qilaylik, biron-bir usul bilan tajriba natijalari intervallarga ajratilgan bo‗lsin. Har bir intervaldagi kuzatilmalarning chastotasini hisoblaymiz. Olingan ma‘lumotlar asosida jadval tuzamiz. Hosil bo‗lgan jadval tanlanma majmua deyiladi. 6.2-misol. Ma‘lum masofa 100 marta o‗lchanganda yo‗l qo‗yilgan xatolar quyidagilardan iborat: Guruhlar Guruhlarda [-20;- Chastotalar [-15;- 2 gi x a t o lar soni 15) 0.02 8 [-10;- 10) 17 [- 0.08 5) 24 0.17 5;0) [0;5) 0.24 26 [5;10 [10;1 13 0.26 ) 0.13 6 [15;2 5) 4 0.06 0] 0.04 Statistik majmuaning grafik tasviri gistogramma deyiladi. Uni qurish uchun t.m.ning qiymatlar sohasini uzunligi h ga teng bo‗lgan k ta oraliqlarga bo‗linadi va kuzatilmalarning har bir oraliqqa tushgan sonlari aniqlanadi. Masalan, n i - soni i - oraliqqa tushgan kuzatilmalar soni b o ‗ l s i n, u holda n 1 n 2 .. . n k n . Chastotalar gistogrammasi deb asoslari oraliq uzunligi h ga teng n i bo‗lgan va balandliklari bo‗lgan to‗g‗ri to‗rtburchaklardan tuzilgan h shaklga aytiladi. Chastotalar gistogrammasi quyidagi ko‗rinishda bo‗ladi:](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img117.jpg)
Teorema(Glivenko-Kantelli). Ixtiyoriy 0 uchun quyidagi
munosabat o‗rinli
€
1 .
l im P s u p F ( x ) F ( x )
n
n
x
Demak n ortgani sari F € ( x ) funksiya F ( x ) ga barcha x larda 1
n
ehtimollik bilan tekis yaqinlashar ekan.
6.4 Gistogramma va poligon
Tajribalar soni katta bo‗lsa, tajriba natijalari statistik qatori ham katta bo‗ladi. Shuning uchun, ko‗p hollarda intervallik statistik qatordan foydalanish maqsadga muvofiq bo‗ladi.
Faraz qilaylik, biron-bir usul bilan tajriba natijalari intervallarga ajratilgan bo‗lsin. Har bir intervaldagi kuzatilmalarning chastotasini hisoblaymiz. Olingan ma‘lumotlar asosida jadval tuzamiz. Hosil bo‗lgan jadval tanlanma majmua deyiladi.
6.2-misol. Ma‘lum masofa 100 marta o‗lchanganda yo‗l qo‗yilgan xatolar quyidagilardan iborat:
Guruhlar
Guruhlarda
[-20;-
Chastotalar
[-15;-
2
gi x a t o lar soni
15)
0.02
8
[-10;-
10)
17
[-
0.08
5)
24
0.17
5;0)
[0;5)
0.24
26
[5;10
[10;1
13
0.26
)
0.13
6
[15;2
5)
4
0.06
0]
0.04
- Statistik majmuaning grafik tasviri gistogramma deyiladi. Uni qurish uchun t.m.ning qiymatlar sohasini uzunligi h ga teng bo‗lgan k ta oraliqlarga bo‗linadi va kuzatilmalarning har bir oraliqqa tushgan sonlari aniqlanadi. Masalan, n i - soni i - oraliqqa tushgan kuzatilmalar soni
b o ‗ l s i n, u holda n 1 n 2 .. . n k n .
Chastotalar gistogrammasi deb asoslari oraliq uzunligi h ga teng
n i
bo‗lgan va balandliklari
bo‗lgan to‗g‗ri to‗rtburchaklardan tuzilgan
h
shaklga aytiladi. Chastotalar gistogrammasi quyidagi ko‗rinishda bo‗ladi:
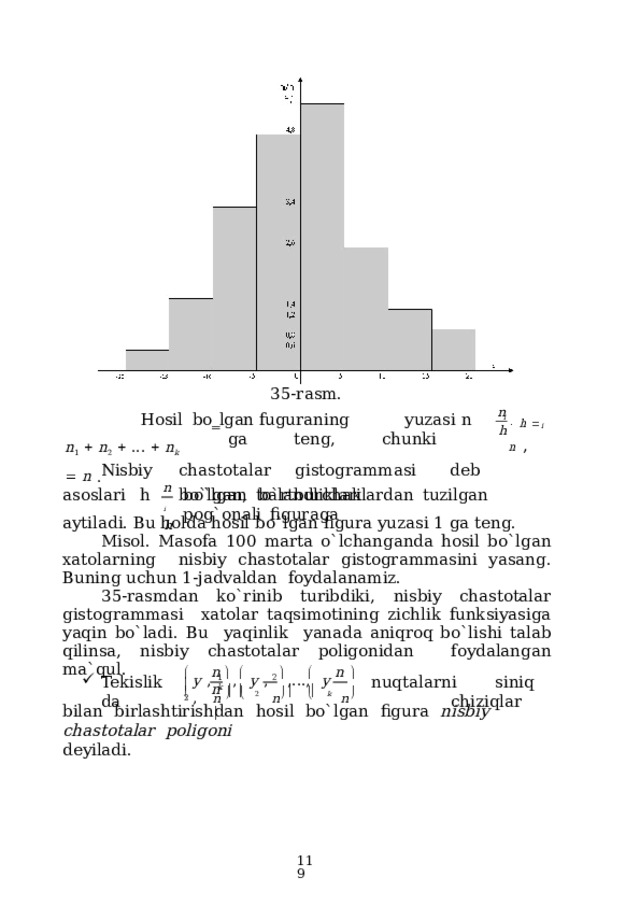
35-rasm.
Hosil bo‗lgan fuguraning yuzasi n ga teng, chunki
n
h n ,
i
i
h
n 1 n 2 .. . n k n .
Nisbiy c h a s t o tal a r g i s t ogra m m a s i d e b a s o s lari h bo` l g a n, balandliklari
n i h
bo`lgan to`rtburchaklardan tuzilgan pog`onali figuraga
aytiladi. Bu holda hosil bo`lgan figura yuzasi 1 ga teng.
Misol. Masofa 100 marta o`lchanganda hosil bo`lgan xatolarning nisbiy chastotalar gistogrammasini yasang. Buning uchun 1-jadvaldan foydalanamiz.
35-rasmdan ko`rinib turibdiki, nisbiy chastotalar gistogrammasi xatolar taqsimotining zichlik funksiyasiga yaqin bo`ladi. Bu yaqinlik yanada aniqroq bo`lishi talab qilinsa, nisbiy chastotalar poligonidan foydalangan ma`qul.
n
n n
nuqt a lar n i s i niq c hiz i q la r
- Tekislikda
y , , y , ,..., y ,
1 2 k
2
n 2 n k n
bilan birlashtirishdan hosil bo`lgan figura nisbiy chastotalar poligoni
deyiladi.
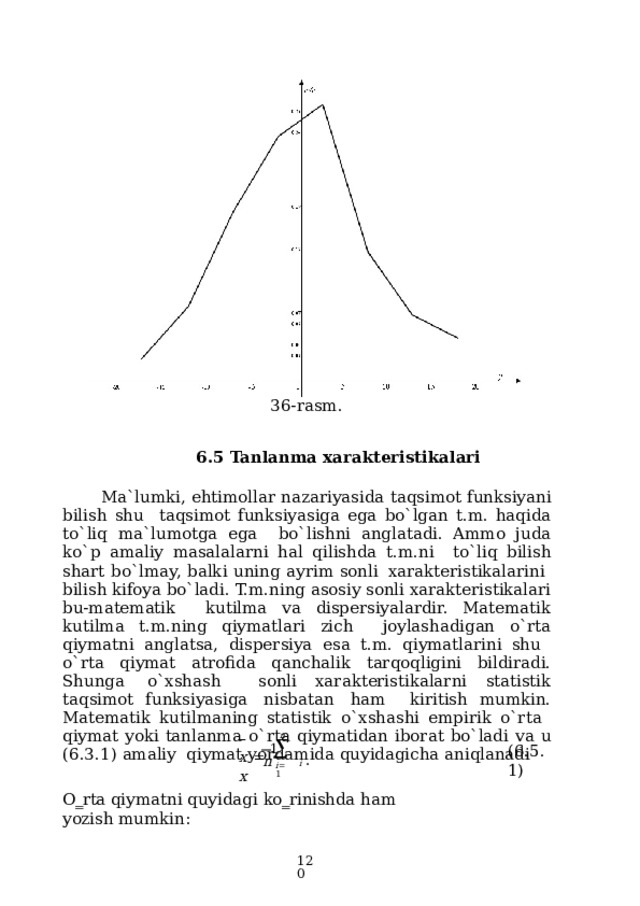
36-rasm.
6.5 Tanlanma xarakteristikalari
Ma`lumki, ehtimollar nazariyasida taqsimot funksiyani bilish shu taqsimot funksiyasiga ega bo`lgan t.m. haqida to`liq ma`lumotga ega bo`lishni anglatadi. Ammo juda ko`p amaliy masalalarni hal qilishda t.m.ni to`liq bilish shart bo`lmay, balki uning ayrim sonli xarakteristikalarini bilish kifoya bo`ladi. T.m.ning asosiy sonli xarakteristikalari bu-matematik kutilma va dispersiyalardir. Matematik kutilma t.m.ning qiymatlari zich joylashadigan o`rta qiymatni anglatsa, dispersiya esa t.m. qiymatlarini shu o`rta qiymat atrofida qanchalik tarqoqligini bildiradi. Shunga o`xshash sonli xarakteristikalarni statistik taqsimot funksiyasiga nisbatan ham kiritish mumkin. Matematik kutilmaning statistik o`xshashi empirik o`rta qiymat yoki tanlanma o`rta qiymatidan iborat bo`ladi va u (6.3.1) amaliy qiymat yordamida quyidagicha aniqlanadi
n
i 1
x 1 x
(6.5. 1 )
i .
n
O‗rta qiymatni quyidagi ko‗rinishda ham yozish mumkin:

k
i i ,
i 1
x 1 x n
( 6 .5.2)
n
bu yerda n i har bir x i variantaning mos chastotasidir.
E m pi r ik d i s p e rsi y a y oki ta n lan m a d i sp e rsi y a s i aniqlanadi:
esa quyidagicha
1
n
S 2 1 x x n
k
n
, (yoki
2
S
x x
) ( 6 .5. 3 )
i
i i
n
i 1
i 1
r-ichi tartibli tanlanma momentlar va markaziy momentlar ham shunga o`xshash aniqlanadi:
n
n
1
1
x x r
x r ,
( 6 .5. 4 )
k
i
n
n
i 1
i 1
Agar tajribalar soni cheksiz katta bo`lsa barcha statistik taqsimot xarakteristikalari nazariy sonli xarakteristikalarga yaqin bo`ladi. Endi shu yaqinlikni o`rganishga kirishamiz.
6.3 – misol. Test natijalariga ko‗ra talabalar quyidagi ballarni yig‗dilar: {5,3,0,1,4,2,5,4,1,5}. Ushbu tanlanmaning sonli xarakteristikalarini hisoblang.
Avval ushbu tanlanmaga mos chastotali taqsimot tuzamiz:
x i
n i
0
1
1
2
2
3
1
4
1
5
2
3
(6.5.2) va (6.5.3) formulalarga asosan:
x 1 0 1 1 2 2 1 3 1 4 2 5 3 3 ,
10
S 2 1 (0 3) 2 1 (1 3) 2 2 (2 3) 2 1 (3 3) 2 1 (4 3) 2 2 (5 3) 2 3 3.2
10
.
VI bobga doir misollar
1. Quyida berilgan tanlanma uchun variatsion qator hamda chastotali taqsimot tuzing: {5,3,7,10,5,5,2,10,7,2,7,7,4,2,4}.

2. Tavakkaliga tanlangan 30 ta talabalarning bo‗y uzunliklaridan iborat quyidagi tanlanma berilgan:
178
157
160
175
154
179
183
165
170
166
156
155
179
159
153
173
167
158
186
182
171
167
175
155
173
163
169
171
172
164
Ushbu tanlanma uchun interval statistik taqsimot tuzing.
3. Chastotali taqsimoti berilgan tanlanmaning empirik taqsimot funksiyasini toping:
a)
b)
X i
n i
15
1
16
17
4
5
18
4
19
2
X i
n i
2
3
1
4
3
5
4
6
6
7
5
8
2
1
4. Quyidagi tanlanma uchun:
X i
n i
0
8
1
2
14
3
20
25
4
30
5
6
24
7
16
12
8
9
7
4
nisbiy chastotali gistogramma yasang.
5. Quyidagi tanlanma uchun:
X i
-3
n i
-2
2
4
-1
5
0
1
6
5
2
3
2
1
poligon yasang.
6.
X i
-1
n i
0
3
6
1
7
2
3
6
4
tanlanmaning sonli xarakteristikalarini hisoblang.
7. Quyidagi tanlanmaning o‗rta qiymati va dispersiyasini hisoblang:

Interval
n i
chegarasi
34-36
36-38
2
3
38-40
40-42
30
42-44
40
44-46
20
5
- Agar har bir variantani a) d songa kattalashtirilsa(yoki kichiklashtirilsa); b) k marta kattalashtirilsa(yoki kichiklashtirilsa) tanlanma o‗rta qiymati va dispersiyasi qanday o‗zgaradi?
- Talabalardan 24 savoldan iborat test sinovi o‗tkazildi. Ushbu test natijalariga ko‗ra talabalar quyidagicha taqsimlanishdi:
To‗g‗ri
T a labal a r soni
jav o b lar soni
2
10-12
4
12-14
14-16
8
16-18
12
18-20
16
20-22
10
3
22-24
Tanlanma sonli xarakteristikalarini hisoblang.
VII bob. Noma’lum parametrlarni baholash
7.1 Statistik baholar va ularning xossalari
Faraz qilaylik, taqsimot funksiyasi noma`lum parametr ga bog`liq bo`lgan t.m. X berilgan bo`lsin. Boshqacha qilib aytganda, kuzatilayotgan
t.m. X ning taqsimot funksiyasi f( x , ) bitta parametrli parametrik taqsimot
funksiyalar oilasiga tegishli bo`lsin. Endi tajriba natijasida olingan ma`lumotlar yordamida noma`lum parametr ni ―tiklash‖, ya`ni ma`lum ma`noda unga yaqin bo`lgan va tajribalar asosida to`liq tiklanadigan biron- bir miqdorni tuzish masalasini ko`raylik. Θ orqali ning qiymatlari to‗plamini belgilaymiz.
Faraz qilaylik, X t.m.ning xajmi n ga teng bo`lgan tanlanmasi bo`lsin.
( X 1 , , X n )
T n T X 1 , , X n
- X 1 , , X n
kuzatilmalarning ixtiyoriy
funksiyasi
statistika deyiladi.
Ta`rifdan kelib chiqadiki, statistika faqat kuzatilmalarga bog`liq bo`lgan tasodifiy miqdor bo`lib, u tajriba natijasida to`liq aniqlanadi.
- Agar T n bo‗lsa, u holda T n statistika noma‘lun parametr uchun
baho deb ataladi.
Ta`rifdan kelib chiqadiki, bitta parametr uchun bir necha statistik baho taklif qilinishi mumkin. Shuning uchun, statistik baholardan ma`lum ma`noda ―yaxshi‖ xossalarga ega bo`lishlari talab etiladi. Odatda har qanday statistik baholarning quyidagi xossalarga ega bo`lishligi maqsadga muvofiqdir.
Siljimagan baho
- Agarda statistik bahoning matematik kutilmasi noma`lum parametrga teng, ya`ni
M T n M T X 1 , , X n
( 7 .1.1)
bo`lsa, statistik baho siljimagan baho deyiladi.
Agar s tat i s t i k b a ho T n T X 1 , , X n u c hun b M T X 1 , , X n 0
bo ` l s a , u s il j igan ba h o d ey il a di va b - s ilj i s h kattaligi bo`lad i .
Nom a ` l um p a r a m e t r X t . m . ni n g m a t e m a tik kut i l m a s i va X 1 , , X n
lar unga mos kuzatilmalar bo`lsin. Quyidagi statistikani kiritamiz
T X 1 , , X n a 1 X 1 .. . a n X n .
( 7 .1.2)
Bu yerda a 1 ,..., a n -lar a 1 ... a n 1 tenglikni qanoatlantiruvchi o`zgarmas
sonlar. va demak, MX 1 ... MX n matematik kutilmani hisoblash
MX
qoidasidan
, X n M a 1 X 1 .. . a n X n a 1 .. . a n a 1 .. . a n
(7.1.3)
M T X 1 ,
ega bo`lamiz. Bu tenglikdan (7.1.2) statistikaning noma`lum parametr u c h un s i lji m a g a n b ah o e k a n l i g i k e l i b ch i q a di. X u s u s a n, a 1 1 , a 2 .. . a n 0
bo ` l sa ( 7 .1. 2 ) d a n T X ,
statistikaga, agarda a ... a 1 bo`lsa
, X n X 1
1 n
n
1
statistikaga ega bo`lamiz. (7.1.3) munosabat a 1 ... a n 1
T X 1 , , X n x
ten g l i k b a jari l a d i g a n i xti y o r iy a 1 , ..., a n lar u ch un t o ` g`ri b o ` l g an l i gi d a n x 1 va x statistikalar ham noma`lum parametr uchun siljimagan baho ekanligi kelib chiqadi. Demak, bitta parametr uchun bir nechta siljimagan
baho tuzish mumkin ekan. Bu xulosadan, tabiiy, siljimagan baholarni taqqoslash zaruriyati kelib chiqadi.
Optimal baho
Noma`lum parametr uchun siljimagan baholar to`plamini U bilan belgilaylik. Oldingi boblardan ma`lumki, t.m. dispersiyasi shu t.m.ning qiymatlari uning matematik kutilmasi atrofida qanchalik zich yoki tarqoq joylashganligining mezoni bo`ladi. Shuning uchun, tabiiy, siljimagan baholarni ularning dispersiyasiga ko`ra taqqoslaymiz.
Faraz qilaylik, T 1 ( X 1 , , X n ) va T 2 ( X 1 , , X n ) lar noma`lum parametr
uchun siljimagan baholar bo`lsin, T 1 ( X 1 , , X n ) U va T 2 ( X 1 , , X n ) U . Agarda shu statistikalar uchun
D T 1 ( X 1 , , X n )D T 2 ( X 1 , , X n )
munosabat bajarilsa, T 1 ( X 1 , , X n ) baho T 2 ( X 1 , , X n ) bahodan aniqroq baho deyiladi.
 0 son uchun , X n l im P { T X 1 , n munosabat o‗rinli bo`lsa, u holda T ( X 1 , , X n ) statistik baho asosli baho deyiladi. Demak, asosli baho T n ( X 1 , , X n ) tajribalar soni ortib borganida noma`lum parametrga ehtimol bo`yicha yaqinlashar ekan. Odatda har qanday statistik bahodan asosli bo`lish talab etiladi. Matematik ststistikada asosli bo`lmagan baholar o`rganilmaydi. 7.1 – misol. Tanlanma o`rta qiymat x noma`lum matematik qurilma MX ga asosli baho ekanligini ko`rsating. Chebishev tengsizligiga va (7.1.3) munosabatga ixtiyoriy kichik 0 son uchun P { x } D x D X . 2 n 2 " width="640"
0 son uchun , X n l im P { T X 1 , n munosabat o‗rinli bo`lsa, u holda T ( X 1 , , X n ) statistik baho asosli baho deyiladi. Demak, asosli baho T n ( X 1 , , X n ) tajribalar soni ortib borganida noma`lum parametrga ehtimol bo`yicha yaqinlashar ekan. Odatda har qanday statistik bahodan asosli bo`lish talab etiladi. Matematik ststistikada asosli bo`lmagan baholar o`rganilmaydi. 7.1 – misol. Tanlanma o`rta qiymat x noma`lum matematik qurilma MX ga asosli baho ekanligini ko`rsating. Chebishev tengsizligiga va (7.1.3) munosabatga ixtiyoriy kichik 0 son uchun P { x } D x D X . 2 n 2 " width="640"
Demak, bitta parametr uchun bir necha siljimagan baholar mavjud bo`lsa, uning statistik bahosi sifatida aniqroq bahoni qabul qilish maqsadga muvofiq bo`ladi. Yuqorida biz noma`lum matematik kutilma uchun ikkita siljimagan X 1 va x -lardan iborat bo`lgan baholarni ko`rdik. Endi ularni taqqoslaylik. Dispersiyani hisoblash qoidasiga asosan:
1
n
1
1
n 2
n
n
( 7 .1.4)
D x D X
x
Dx D
i
i
n
i 1
i 1
va DX 1 DX bo`ladi. yuqorida keltirilgan taqqoslash qoidasiga muvofiq, ko`rinib turibdiki x baho X 1 bahoga nisbatan aniqroq bo`ladi.
- Ag a r
i n f D T X 1 , , X n D T X , , X n
T ( X 1 , , X n ) U bo`lsa,
*
1
, X n - s tatis t ik ba h o o pt i mal ba h o d ey il a di.
T * X ,
1
Ko`rsatish mumkinki x statistika noma`lum matematik kutilma
uchun barcha siljimagan chiziqli baholar ichida eng aniq (optimal) bahodir.
Asosli baho
- Agarda n cheksizlikka intilganda T ( X 1 , , X n ) statistika ehtimol bo`yicha noma`lum parametr ga yaqinlashsa, ya`ni ixtiyoriy kichik 0 son uchun
, X n
l im P { T X 1 ,
n
munosabat o‗rinli bo`lsa, u holda T ( X 1 , , X n ) statistik baho asosli baho
deyiladi.
Demak, asosli baho T n ( X 1 , , X n ) tajribalar soni ortib borganida
noma`lum parametrga ehtimol bo`yicha yaqinlashar ekan. Odatda har qanday statistik bahodan asosli bo`lish talab etiladi. Matematik ststistikada asosli bo`lmagan baholar o`rganilmaydi.
7.1 – misol. Tanlanma o`rta qiymat x noma`lum matematik qurilma
MX ga asosli baho ekanligini ko`rsating.
Chebishev tengsizligiga va (7.1.3) munosabatga ixtiyoriy kichik 0 son uchun
P { x } D x D X .
2
n 2
 0 uchun Chebishev tengsizligidan quyidagi tengsizlikni yoza olamiz: P { T DT n . (7.1.5) 2 n Am m o, s h a r t ga ko ` r a , i x ti yo r i y ta y inl a ng a n 0 u c h u n n da DT n 0. 2 Demak, (7.1.5) tengsizlikdan T ( X 1 ,..., X n ) statistikaning asosli baho ekanligi kelib chiqadi. Nuqtaviy baholash usullari Nuqtaviy baholash usullari Biz oldingi paragraflarda statistik baholar va ularning xossalari bilan tanishdik. Statistik baholar qanday topiladi? Mana shu savolga javob beramiz. Statistik baholar tuzishning ikki usulini ko`rib chiqamiz. Momentlar usuli Momentlar usuli Momentlar usuli Faraz qilaylik, X kuzatilmalari X 1 ,..., X n lardan iborat va taqsimot funksiyasi F x , noma`lum parametr ,..., ga bog`liq bo`lgan t.m. 1 r bo`lsin. Birinchi bobda tanlanma momentlar tushunchalarini kiritdik va ularning ayrim xossalari bilan tanishdik. Xususan, KSQ ga asosan tanlanma momentlar tajribalar soni katta bo`lganida nazariy momentlarga istalgancha yaqin bo`lishligini bildik. Momentlar usuli asosida mana shu yaqinlik g`oyasi yotadi. " width="640"
0 uchun Chebishev tengsizligidan quyidagi tengsizlikni yoza olamiz: P { T DT n . (7.1.5) 2 n Am m o, s h a r t ga ko ` r a , i x ti yo r i y ta y inl a ng a n 0 u c h u n n da DT n 0. 2 Demak, (7.1.5) tengsizlikdan T ( X 1 ,..., X n ) statistikaning asosli baho ekanligi kelib chiqadi. Nuqtaviy baholash usullari Nuqtaviy baholash usullari Biz oldingi paragraflarda statistik baholar va ularning xossalari bilan tanishdik. Statistik baholar qanday topiladi? Mana shu savolga javob beramiz. Statistik baholar tuzishning ikki usulini ko`rib chiqamiz. Momentlar usuli Momentlar usuli Momentlar usuli Faraz qilaylik, X kuzatilmalari X 1 ,..., X n lardan iborat va taqsimot funksiyasi F x , noma`lum parametr ,..., ga bog`liq bo`lgan t.m. 1 r bo`lsin. Birinchi bobda tanlanma momentlar tushunchalarini kiritdik va ularning ayrim xossalari bilan tanishdik. Xususan, KSQ ga asosan tanlanma momentlar tajribalar soni katta bo`lganida nazariy momentlarga istalgancha yaqin bo`lishligini bildik. Momentlar usuli asosida mana shu yaqinlik g`oyasi yotadi. " width="640"
Oxirgi tengsizlikda dispersiya chekli bo`lsa, n da limitga o`tsak, haqiqatan ham x statistikaning asosli baholigi kelib chiqadi.
Umuman, ixtiyoriy siljimagan baho T ( X 1 , , X n ) ning noma`lum
parametrga asosli baho bo`lishlik shartini keltiramiz.
Teorema. Agar T n T ( X 1 , , X n ) statistika parametr uchun
siljimagan baho bo`lib, n uning dispersiyasi DT n 0 bo`lsa, u holda u asosli baho bo`ladi.
Isbot. T ( X 1 , , X n ) statistika siljimagan baho bo`lgani uchun
MT ( X 1 , , X n ) . U holda ixtiyoriy 0 uchun Chebishev tengsizligidan quyidagi tengsizlikni yoza olamiz:
P { T DT n . (7.1.5)
2
n
Am m o, s h a r t ga ko ` r a , i x ti yo r i y ta y inl a ng a n 0 u c h u n n da
DT n 0.
2
Demak, (7.1.5) tengsizlikdan T ( X 1 ,..., X n ) statistikaning asosli baho ekanligi kelib chiqadi.
- Nuqtaviy baholash usullari
- Nuqtaviy baholash usullari
Biz oldingi paragraflarda statistik baholar va ularning xossalari bilan tanishdik. Statistik baholar qanday topiladi? Mana shu savolga javob beramiz. Statistik baholar tuzishning ikki usulini ko`rib chiqamiz.
- Momentlar usuli
- Momentlar usuli
- Momentlar usuli
Faraz qilaylik, X kuzatilmalari X 1 ,..., X n lardan iborat va taqsimot
funksiyasi F x , noma`lum parametr ,..., ga bog`liq bo`lgan t.m.
1 r
bo`lsin. Birinchi bobda tanlanma momentlar tushunchalarini kiritdik va ularning ayrim xossalari bilan tanishdik. Xususan, KSQ ga asosan tanlanma momentlar tajribalar soni katta bo`lganida nazariy momentlarga istalgancha yaqin bo`lishligini bildik. Momentlar usuli asosida mana shu yaqinlik g`oyasi yotadi.
ta k MX ,
k
Faraz qilaylik X tasodifiy miqdorning birinchi r
k 1 , ... , r
m o m e ntl a ri m a v j u d bo ` l s i n. T a bi i y k i, ular no m a ` l u m
n
n k
k
A X , k 1 , . . ., r
funksiyalari bo`ladilar.
parametrning
,
k k
i
i 1
tanlanma momentlarini mos ravishda k , k 1,..., r , larda tenglashtirib r ta tenglamalar sistemasini tuzib olamiz:
1 ( ) A n 1 ,
( ) A ,
2 n 2
( 7 .2.1)
.................
r ( ) A n r .
larga nisbatan yechib,
Mana shu tenglamalar sistemasini
1 , ... , r
k k ( X 1 ,
k 1 , ... , r
, X n ), k 1,..., r yechimlarga ega bo‗lamiz. Shunday topilgan k ,
statistikalar momentlar usuli bilan noma‘lum k ,
k 1 , ... , r
paramertlar uchun tuzilgan statistik baholar bo‗ladi.
7.2 - misol. Matematik kutilmasi va dispersiyasi no‗malum bo‗lgan,
( x 1 ) 2
1
2 2
e
z ichlik fun k s iy a s i f ( x , )
bo‗lgan normal qonunni qaraylik.
2 2
Noma‘lum 1 va 2 parametrlarni momentlar usulida baholaylik. Bu holda (7.2.1) tenglamalar quyidagi ko‗rinishda bo‗ladi
1 A n 1 va A .
2
2 1 n 2
Natijada momentlar usuli bilan tuzilgan statistik baholar
1
1
n
n
n
n
i
X i x , 2
( X x ) 2 S 2
1
i 1 i 1
ko‗rinishda bo‗ladi.
Momentlar usuli bilan topilgan statistik baholar ayrim hollarda siljimagan, asosli va eng aniq baholar bo‗ladi.
II. Haqiqatga maksimal o‘xshashlik usuli
Kuzatilmalari X 1 ,..., X n lardan va umumlashgan zichlik funksiyasi p ( x , ) dan iborat X t.m.ni olaylik. Agar X diskret t.m. bo‗lsa, p ( x , ) P { X x ; } ehtimolliklardan, X uzluksiz t.m. bo‗lgan holda esa

p ( x , ) f ( x ; ) zichlik funksiyadan iborat bo‗ladi. Quyidagi funksiyaga L ( x 1 ,..., x n , ) p ( x 1 , ) ... p ( x n , ) haqiqatga maksimal o‗xshashlik funksiyasi deyiladi. Faraz qilaylik, L ( x 1 ,..., x n , ) funksiya yopiq sohada biror
* nuqtada eng katta qiymatga erishsin:
L ( x , ... , x , ) m a x L ( x , ... , x , )
*
.
1 n
1 n
Haqiqatga maksimal o‗xshashlik funksiyasi eng katta qiymatga e r i s h a d i g a n * qiy m at n o m a ‘ l um p a ra m e tr u ch un h a q i q a tga m a k s i m a l o‗xshashlik usuli bilan tuzilgan statistik baholar deb ataladi. Ularni quyidagi tenglamalr sistemasidan ham topish mumkin:
L ( x 1 , ... , x n , )
k
(7.2.2)
0 , k 1 , .. . r .
*
(7.2.2) tenglamalar sistemasi haqiqatga maksimal o‗xshashlik tenglamalri deyiladi.
K o ‗ p oll ar da ( 7 . 2.2) ten g la m a lar si ste m a s i o ‗ r ni g a qu y i d ag i
tenglamar sistemasini yechish qulay bo‗ladi:
l n L ( x 1 , ... , x n , )
k
(7.2.3)
0 , k 1 , .. . r .
*
7.3 -misol. Matematik kutilmasi va dispersiyasi noma‘lum bo‗lgan,
( x 1 ) 2
1
2 2
f ( x , ) e
zichlik funksiyasi
bo‗lgan normal qonunni olaylik.
2 2
Haqiqatga maksimal o‗xshashlik funksiyasini tuzamiz:
( X i 1 ) 2
1
n n
L ( x 1 , ... , x n , ) f ( X i , )
i 1 i 1
2 2
e
2
2 2
2
1 1
n
( X 1 ) .
n
i i 1
e x p
2
2
2 2
2
B und a n

( X ) 2
n
n
1 n 2
i 1
l n L ( x , ... , x , ) l n 2 n l n
.
i 1
2
2
2
2
Avval (7.2.3) sistemaning birinchi tenglamasini qaraylik:
ln L ( x 1 ,..., x n , ) 1
n
i 1 .
2( X ) 0
2
2 i 1
1
n
Soddalashtirgandan so‗ng X i n 1 0 tenglamaga kelamiz.
i 1
Endi (7.2.3) sistemaning ikkinchi tenglamasini tuzamiz:
ln L ( x 1 ,..., x n , ) 1 1
n
i 1
i 1
( X ) 0 .
n
2
3
2 2
k
n
Soddalashtirgandan so‗ng ( X i 1
) n 0
2
2
tenglamaga kelamiz.
2
i 1
Natijada va lar uchun
2
1 2
1
1
n
n
n
n
X x ,
2
( X x ) 2 S 2
i
i
1
2
i 1
i 1
Ko‗rinishdagi statistik baholarni topamiz.
Demak, normal qonun uchun momentlar va haqiqatga maksimal o‗xshashlik usullari bilan tuzilgan statistik baholar aynan bir xil ekan.
7.3 Interval baholash Ishonchlilik oralig‘i
Oldingi paragraflarda biz noma‘lum parametrlarning nuqtaviy
statistik baholari bilan tanishdik. Tuzilgan nuqtaviy baholar tanlanmaning aniq funksiyalari bo‗lgan t.m. bo‗lib, ular noma‘lum parametrlarning asl qiymatiga yaqin bo‗lgan nuqtani aniqlab beradi xolos. Ko‗p masalalarda noma‘lum parametrlarni statistik baholash bilan birgalikda bu bahoning aniqligini, ishonchliligini topish talab etiladi. Matematik statistikada
 0 sonini topish lozim bo‗lsin. Bu munosabatni boshqa ko‗rinishda yozamiz P{ T ( X 1 , , X n )– δ θ T ( X 1 , , X n )+ δ }= β (7.3.1) (7.3.1) tenglik noma‘lum θ parametrning qiymati β ehtimollik bilan ℮ β =( T ( X 1 , , X n )– δ ; T ( X 1 , , X n )+ δ ) (7.3.2) oraliqda ekanligini anglatadi. Shuni aytish joizki, (7.3.2) dagi ℮ β – oraliq tasodifiy miqdorlardan iborat chegaralarga ega. Shuning uchun, β – ehtimollikni noma‘lum θ parametrning aniq qiymati ℮ β – oraliqda yotish ehtimoli deb emas, balki ℮ β – oraliq θ nuqtani o‗z ichiga olish ehtimoli deb talqin qilish to‗g‗ri bo‗ladi (37 – rasm). ℮ β • • • , X n ) – δ θ T ( X 1 , , X n ) + δ T ( X 1 , 37 – rasm. Demak, aniqlangan ℮ β oralig‗i ishonchlilik oralig‗i, β – ehtimol esa ishonchlilik ehtimoli deyiladi. " width="640"
0 sonini topish lozim bo‗lsin. Bu munosabatni boshqa ko‗rinishda yozamiz P{ T ( X 1 , , X n )– δ θ T ( X 1 , , X n )+ δ }= β (7.3.1) (7.3.1) tenglik noma‘lum θ parametrning qiymati β ehtimollik bilan ℮ β =( T ( X 1 , , X n )– δ ; T ( X 1 , , X n )+ δ ) (7.3.2) oraliqda ekanligini anglatadi. Shuni aytish joizki, (7.3.2) dagi ℮ β – oraliq tasodifiy miqdorlardan iborat chegaralarga ega. Shuning uchun, β – ehtimollikni noma‘lum θ parametrning aniq qiymati ℮ β – oraliqda yotish ehtimoli deb emas, balki ℮ β – oraliq θ nuqtani o‗z ichiga olish ehtimoli deb talqin qilish to‗g‗ri bo‗ladi (37 – rasm). ℮ β • • • , X n ) – δ θ T ( X 1 , , X n ) + δ T ( X 1 , 37 – rasm. Demak, aniqlangan ℮ β oralig‗i ishonchlilik oralig‗i, β – ehtimol esa ishonchlilik ehtimoli deyiladi. " width="640"
statistik baholarning aniqligini topish ishonchlilik oralig‗i va unga mos ishonchlilik ehtimolligi orqali hal etiladi.
Faraz qilaylik, tanlanma yordamida noma‘lum θ parametr uchun
siljimagan T ( X 1 , , X n ) baho tuzilgan bo‗lsin. Tabiiyki │ T ( X 1 , , X n ) – θ │
ifoda noma‘lum θ parametr bahosining aniqlik darajasini belgilaydi. T ( X 1 , , X n ) statistik bahoning noma‘lum θ parametrga qanchalik yaqinligini aniqlash masalasi qo‗yilsin. Oldindan biron-bir β (0β
Ρ{│ T ( X 1 , , X n ) – θ │δ }= β
munosabat o‗rinli bo‗ladigan δ 0 sonini topish lozim bo‗lsin. Bu munosabatni boshqa ko‗rinishda yozamiz
P{ T ( X 1 , , X n )– δ θ T ( X 1 , , X n )+ δ }= β (7.3.1)
(7.3.1) tenglik noma‘lum θ parametrning qiymati β ehtimollik bilan
℮ β =( T ( X 1 , , X n )– δ ; T ( X 1 , , X n )+ δ ) (7.3.2)
oraliqda ekanligini anglatadi.
Shuni aytish joizki, (7.3.2) dagi ℮ β – oraliq tasodifiy miqdorlardan iborat chegaralarga ega. Shuning uchun, β – ehtimollikni noma‘lum θ parametrning aniq qiymati ℮ β – oraliqda yotish ehtimoli deb emas, balki ℮ β
– oraliq θ nuqtani o‗z ichiga olish ehtimoli deb talqin qilish to‗g‗ri bo‗ladi
(37 – rasm).
℮ β
•
•
•
, X n ) – δ
θ
T ( X 1 ,
, X n ) + δ
T ( X 1 ,
37 – rasm.
- Demak, aniqlangan ℮ β oralig‗i ishonchlilik oralig‗i, β – ehtimol esa
ishonchlilik ehtimoli deyiladi.
 0 sonni shunday topaylikki, u uchun quyidagi munosabat o‗rinli bo‗lsin: P x a . ( 7 .3.3) x - t.m.ning taqsimot funksiyasi normal qonunga yaqinligini hisobga olib, (7.3.3) – tengsizlikning o‗ng tomondagi β – sonini Laplas funksiyasi bilan bog‗laymiz: P x a . (7.3.4) 2 2 x x 2 n - o‗rta kvadratik chetlanish. B u ye r d a x Laplas funksiyasining Φ ( -x ) = 1– Φ ( x ) xossasini inobatga olsak, (7.3.4) - tenglikni quyidagicha yozish mumkin: x a 2 1 P ( 7 .3.5) 2 x (7.3.3) va (7.3.5) tengliklardan quyidagini hosil qilamiz: " width="640"
0 sonni shunday topaylikki, u uchun quyidagi munosabat o‗rinli bo‗lsin: P x a . ( 7 .3.3) x - t.m.ning taqsimot funksiyasi normal qonunga yaqinligini hisobga olib, (7.3.3) – tengsizlikning o‗ng tomondagi β – sonini Laplas funksiyasi bilan bog‗laymiz: P x a . (7.3.4) 2 2 x x 2 n - o‗rta kvadratik chetlanish. B u ye r d a x Laplas funksiyasining Φ ( -x ) = 1– Φ ( x ) xossasini inobatga olsak, (7.3.4) - tenglikni quyidagicha yozish mumkin: x a 2 1 P ( 7 .3.5) 2 x (7.3.3) va (7.3.5) tengliklardan quyidagini hosil qilamiz: " width="640"
Matematik kutilma uchun ishonchlilik oralig‘i
Faraz qilaylik, X tasodifiy miqdorning matematik kutilmasi θ va dispersiyasi σ bo‗lsin. Noma‘lum θ – parametr uchun ishonchlilik ehtimoli β – ga teng bo‗lgan ℮ β – ishonchlilik oralig‗ini tuzish masalasini qaraylik.
X 1 , …, X n – hajmi n – ga teng bo‗lgan tanlanma va unga mos
tanlanma o‗rta qiymati va dispersiyasini tuzaylik:
2
n
x 1 X , S 2 1 n ( X x ) 2 .
i
i 1
i
n
n
i 1
Eslatib o‗tamiz, x – bir xil taqsimlangan, bog‗liqsiz tasodifiy miqdorlar yig‗indisidantuzilgandir. Shuning uchun, markaziy limit teoremaga asosan uning taqsimot funksiyasi normal qonunga yaqindir. x ning matematik kutilmasini va dispersiyasini hisoblaymiz:
2
M x , D x
n
Endi δ β 0 sonni shunday topaylikki, u uchun quyidagi munosabat o‗rinli bo‗lsin:
P x a .
( 7 .3.3)
x - t.m.ning taqsimot funksiyasi normal qonunga yaqinligini hisobga olib, (7.3.3) – tengsizlikning o‗ng tomondagi β – sonini Laplas funksiyasi bilan bog‗laymiz:
P x a
.
(7.3.4)
2
2
x
x
2
n
- o‗rta kvadratik chetlanish.
B u ye r d a
x
Laplas funksiyasining Φ ( -x ) = 1– Φ ( x ) xossasini inobatga olsak, (7.3.4) - tenglikni quyidagicha yozish mumkin:
x a 2
1
P
( 7 .3.5)
2
x
(7.3.3) va (7.3.5) tengliklardan quyidagini hosil qilamiz:

1
.
2
2
x
Oxirgi tenglikdan δ β ni aniqlaymiz:
1
x 2
1
( 7 .3.6)
2
Bu yerda Φ -1 ( x ) orqali Laplas funksiyasiga teskari funksiyani belgiladik. (7.3.6) – tenglik bilan aniqlangan δ β – soni noma‘lum x miqdor orqali yoziladi. Yetarli katta n lar uchun tanlanma dispersiya S 2
S 2
n
nazariy dispersiyaga yaqin bo‗lgani uchun
deyish mumkin, ya‘ni
S 2
ni taqriban
ga teng
x
x
n
Shunday qilib, noma‘lum o‗rta qiymat θ – uchun β – ishonchlilik ehtimoliga teng ℮ β – ishonchlilik oralig‗i
℮ β = x , x
( 7 .3.7)
2
2 S 1
ga teng bo‗ladi. Bu yerda
.
n
7.4 -misol. X t.m.ning tajriba natijasida 20 ta qiymati olindi.
i
X i
1
10.9
i
2
3
10.7
11
X i
11.0
12
10.8
4
13
5
10.3
10.5
10.5
14
10.6
6
10.4
7
15
10.8
16
8
11.3
10.9
10.8
9
17
10.6
18
11.2
10
11.3
19
10.9
10.8
20
10.9
10.7

X t.m.ning matematik kutilmasi θ uchun β = 0.86 ishonchlilik ehtimoliga mos keluvchi ishonchlilk oralig‗ini tuzing.
Tanlanma o‗rta qiymat va dispersiyani topamiz.
20
X 1 0 . 78
2 0 1
20
2
i i 1
i
X 10.78 0.064 ;
X 1
20
2
2
S
;
1 9 2 0 i 1
S 2
n
0.0564 .
x
(7.3.7) formula bo‗yicha ishonchlilik oralig‗ini tuzamiz:
0.0564 2 1 0.86 0.083 va x 10.78 0.083 10.70 ;
x 1 0 . 7 8 0 . 0 8 3 1 0 . 8 6 ,
u holda ishonchlilk oralig‗i ℮ β =(10.70; 10.86) ekan.
Normal taqsimot matematik kutilmasi uchun ishonchlilik oralig‘i. Styudent taqsimoti
Oldingi paragraflarda biz taqsimoti funksiyasi ixtiyoriy bo‗lgan t.m. matematik kutilmasi uchun taqribiy ishonchlilik oralig‗i tuzdik. Agarda tanlanma o‗rta qiymatining taqsimoti ma‘lum bo‗lsa, aniq ishonchlilik oralig‗ini tuzish mumkin.
Faraz qilaylik, X 1 , …, X n lar matematik kutilmasi θ va dispersiyasi σ 2 bo‗lgan normal qonun bo‗yicha taqsimlangan X t.m.ning tajribalar natijasida olingan hajmi n – ga teng bo‗lgan tanlanmasi bo‗lsin.
Quyidagi statistikani kiritamiz:
n 1 x
S
( 7 .3.8)
t
Bu yerda,
1
n
n
1
n
S 2 x x .
x i
i 1
2
x
,
i
n 1
i 1
Teorema. Agarda X 1 , X 2 , …, X n – bog‗liqsiz va ( θ , σ 2 ) parametrli normal qonun bo‗yicha taqsimlan statistik tanlanma bo‗lsa, u holda t – statistika erkinlik darajasi n- 1 ga teng bo‗lgan Styudent taqsimotiga ega bo‗ladi.

Styu d en t bo‗ladi:
zichlik
f u nk s iy a s i
qu y d a gi
ko‗rinishda
taqsimotining
n
- n
2
t 2
2
S n 1 t
1
n 1
( n 1 ) n 1
2
funksiya yuqoridagi formuladan ko‗rinib
( x ) u x 1 e u d u -
g a m m a
0
turibdiki, Styudent taqsimoti x va S statistikalarga bog‗liq bo‗lmay, faqat kuzatilmalar hajmi n ga bog‗liqdir.
Endi Styudent taqsimotining ishonchlilik oralig‗i qurishga tadbiqini ko‗raylik.
Normal qonun bo‗yich taqsimlangan X t.m.ning tajribalar natijasida
X 1 , , X n qiymatlari topilgan bo‗lsin. Bular asosida x va S statistikalarni hisoblaymiz. T.m. noma‘lum matematik kutilmasi θ – uchun ishonchlilik ehtimoli β (0β ℮ β ishonchlilik oralig‗ini qurish masalasini qaraylik.
Quyidagi ehtimolni ko‘raylik:
P x .
Bu tenglikning chap tomonida x t.m.dan t – statistikaga o‗tamiz.
n S
ga
tengsizlikning ikkala tomonini
B uning u ch un
x
ko‗paytiramiz.U holda,
n x
P
S
S
n
tenglik hosil bo‗ladi. (7.3.8) formuladan foydalansak,
P t
S
n
munosabatga kelamiz.
Styudent taqsimoti zichlik funksiyasining juftligidan foydalanib quyidagini hosil qilamiz:

t
P t t 2 S n 1 ( t ) d t
( 7 .3.9)
0
Endi (7.3.9) tenglikdan t β ni topishiniz mumkin. Styudent taqsimoti qiymatlari jadvaldan foydalanib, ishonchlilik ehtimoli β va erkinlik darajasi n- 1 ga mos t β ni aniqlaymiz:
S
n
t
Bu esa ℮ β ishonchlilik oralig‗i uzunligining yarmiga teng Demak,
~ ~
S
n n
S
x t
, x t
.
℮ =
β
7.5 - misol. ( θ , σ 2 ) parametrli normal qonun bo‗yicha taqsimlangan
X t.m.ning 10 ta bog‗liqsiz tajribalar natijasida quyidagi qiymatlari topildi:
i
X i
1
2
2.5
2
3
4
-2.3
1.9
5
-2.1
6
7
2.4
8
2.3
-2.5
9
10
1.5
-1.7
matematik kutilma θ uchun ishonchlilik ehtimoli β = 0.95 bo‗lgan ℮ β – ishonchlilik oralig‗ini toping.
Tanlanmaning o‗rta qiymati va dispersiyasini topamiz:
1
10
x x i 0 .4 ,
1 0 1
10
i
x ( 0.4 ) 4.93 3 .
2 2
S
10 i 1 9 10 i 1
Jadvaldan erkinlik darajasi n- 1=9 va ehtimollik β = 0.95 bo‗yicha Styudent taqsimotining (1 -t β ) – kvantilini topamiz t β =2.26. Demak,
S
t 1.58
n
va izl a n ay ot g a n i s hon ch li l ik oral i g ‗ i ℮ β = x , x = ( - 1.18; 1 . 9 8) ko‗rinishda bo‗lar ekan.
![VII bobga doir misollar 1. Binomial taqsimot baho bo‗la oladimi? n 1 parametrik uchun Т X 1 s tati s tika n i n i 1 Empirik taqsimot funksiyaning siljimagan va asosli baho ekanini ko‗rsating. Agar ixtiyoriy taqsimotga ega bo‗lsa, a M vа D lar u c hun x , S 2 lar qan d a y baho b o ‗ lad i ? tanlanma [0, ] oraliqda tekis taqsimlangan bo‗lsa, 4. X 1 , . .. , X n parametr uchun quyidagi baholarning siljimaganlik va asoslilik xossalarini tekshiring: a) 2 x ; n / 2 ; c ) ( n 1 ) X b) x X ; d) X X ; e) X ( 1 ) ( n ) ( n ) ( 1 ) ( n ) n 1 uchun haqiqatga maksimal o‗xshashlik 5 . B i ( 1 , ) m od e l d a bahosi toping. 6. П ( ) modelda noma‘lum parametrini baholang va xossalarga tekshiring. 7 . m od e l d a h a qi q at ga m a k s im a l o ‗ x s h a s hl i k b ah o s i E ( ) toping. 8 . Mo m e ntl a r u s u l i d a n f o y d a lanib, a ) [ 0, ] ; b) [ 0 , 2 ] ; c ) [ - 1, + 1 ] ; d) [ - , ] orali q da gi tek i s ta q si m ot no m a ‘ l um p a r a m e t ri ni baholang. 9. Agar т.м. kuzatish natijasida olingan tanlanma X ( n ) ( X ,... , X ) 1 n X ( n ) m a x ( X 1 , . .. , X n ) bo‗lsa, vа X (1) min( X 1 ,..., X n ) -statistikalarning taqsimot funksuyasini toping. X t.m. o‗rtacha kvadratik chetlashishi σ =3 ma‘lum bo‗lgan normal taqsimotga ega. Tanlanma hajmi n =36 va bahoning ishonchliligi γ=0,95 berilgan. Noma‘lum a matematik kutilma uchun ishonch intervalini tuzing. Quyida tasodifan tanlangan 100 ta talabaning bo‗ylari haqidagi ma‘lumotlar keltirilgan: X i n i 154- 10 158- 158 14 162 162- 166 166- 26 170 170- 28 174 174- 12 178 178- 8 2 182](https://fsd.multiurok.ru/html/2022/04/26/s_62681c75b8bd5/img136.jpg)
VII bobga doir misollar
1. Binomial taqsimot
baho bo‗la oladimi?
n
1
parametrik uchun Т
X 1 s tati s tika
n
i
n
i 1
- Empirik taqsimot funksiyaning siljimagan va asosli baho ekanini ko‗rsating.
- Agar ixtiyoriy taqsimotga ega bo‗lsa, a M vа D lar
u c hun x , S 2 lar qan d a y baho b o ‗ lad i ?
tanlanma [0, ] oraliqda tekis taqsimlangan bo‗lsa,
4.
X 1 , . .. , X n
parametr uchun quyidagi baholarning siljimaganlik va asoslilik xossalarini tekshiring: a) 2 x ;
n
/ 2 ; c ) ( n 1 ) X
b) x X
; d) X X ; e)
X
( 1 )
( n )
( n )
( 1 ) ( n )
n 1
uchun haqiqatga maksimal o‗xshashlik
5 . B i ( 1 , ) m od e l d a
bahosi toping.
6. П ( ) modelda noma‘lum parametrini baholang va xossalarga
tekshiring.
7 . m od e l d a h a qi q at ga m a k s im a l o ‗ x s h a s hl i k b ah o s i
E ( )
toping.
8 . Mo m e ntl a r u s u l i d a n f o y d a lanib, a ) [ 0, ] ; b) [ 0 , 2 ] ; c ) [ - 1,
+ 1 ] ; d) [ - , ] orali q da gi tek i s ta q si m ot no m a ‘ l um p a r a m e t ri ni baholang.
9. Agar т.м. kuzatish natijasida olingan tanlanma
X ( n ) ( X ,... , X )
1 n
X ( n ) m a x ( X 1 , . .. , X n )
bo‗lsa, vа X (1) min( X 1 ,..., X n ) -statistikalarning
taqsimot funksuyasini toping.
- X t.m. o‗rtacha kvadratik chetlashishi σ =3 ma‘lum bo‗lgan normal taqsimotga ega. Tanlanma hajmi n =36 va bahoning ishonchliligi γ=0,95 berilgan. Noma‘lum a matematik kutilma uchun ishonch intervalini tuzing.
- Quyida tasodifan tanlangan 100 ta talabaning bo‗ylari haqidagi ma‘lumotlar keltirilgan:
X i
n i
154-
10
158-
158
14
162
162-
166
166-
26
170
170-
28
174
174-
12
178
178-
8
2
182

Talabalarning bo‗yi ( a , 2 ) parametrli normal taqsimotga ega va o‗rtacha bo‗y a x ma‘lum deb olib, 2 uchun ishonchlilik intervalini tuzing(γ=0,995).
VIII bob. Statistik gipotezalarni tekshirish
- Statistik gipotezalar. Statistik gipotezalarni tekshirish alomatlari va ularning xossalari
- Statistik gipotezalar. Statistik gipotezalarni tekshirish alomatlari va ularning xossalari
Ko‗p hollarda tajribalardan olingan ma‘lumotlar asosida o‗rganilayotgan tasodif bilan bog‗liq bo‗lgan jarayonlar xarakteristikalari haqida bir yoki bir necha turli gipotezalar(tahminlar) qilish mumkin. Statistik ma‘lumotlar asosida tasodifiy jarayon taqsimoti yoki boshqa xarakteristikalari haqida aytilgan gipotezalarni tekshirishni matematik statistikaning statistik gipotezalar nazariyasi bo‗limi o‗rganadi.
- Kuzatilayotgan t.m. haqida aytilgan ixtiyoriy fikrga statistik gipoteza
- Kuzatilayotgan t.m. haqida aytilgan ixtiyoriy fikrga statistik gipoteza
- Kuzatilayotgan t.m. haqida aytilgan ixtiyoriy fikrga statistik gipoteza
deyiladi.
8.1-misol . Hosildorligi a 0 bo‗lgan bug‗doy navini hosildorligi a 1 bo‗lgan bug‗doy navi bilan solishtirilmoqda. Ma‘lum tumanda birinchi nav bug‗doy ikkinchi navga qaraganda ko‗proq hosil beradi degan gipotezani tekshirish kerak.
Keltirilgan misoldan ko‗rinib turibdiki, mavjud bo‗lishi mumkin bo‗lgan gipotezalar turlicha bo‗lishi mumkin. Biron – bir obyekt haqida aytilgan gipoteza statistik ma‘lumotlar asosida tekshirilishi mumkin.
- Tekshirilishi kerak bo‗lgan gipoteza asosiy gipoteza deyiladi va u H 0 bilan belgilanadi. Asosiy gipotezadan qarama-qarshi bo‗lgan ixtiyoriy gipotezaga raqobatlashuvchi yoki alternativ gipoteza deb ataladi.
- Tekshirilishi kerak bo‗lgan gipoteza asosiy gipoteza deyiladi va u H 0 bilan belgilanadi. Asosiy gipotezadan qarama-qarshi bo‗lgan ixtiyoriy gipotezaga raqobatlashuvchi yoki alternativ gipoteza deb ataladi.
- Tekshirilishi kerak bo‗lgan gipoteza asosiy gipoteza deyiladi va u H 0 bilan belgilanadi. Asosiy gipotezadan qarama-qarshi bo‗lgan ixtiyoriy gipotezaga raqobatlashuvchi yoki alternativ gipoteza deb ataladi.
Afsuski, statistik ma‘lumotlar asosida aniq va qat‘iy bir yechimga kelish qiyin, shuning uchun har qanday yechimda ma‘lum xatolikka yo‗l qo‗yish mumkin. Matematik statistikada statistik gipotezalarni tekshirishda ikki xil xatolikka yo‗l qo‗yishi mumkin. Statistik yechim asosida asosiy faraz u to‗g‗ri bo‗lgan holda ham rad etilishi mumkin. Bunday xatolik birinchi tur xatolik deyiladi. Statistik yechim asosida alternativ gipoteza to‗g‗ri bo‗lsa ham rad etilishi mumkin. Bunday xatolik ikkinchi tur xatolik deyiladi. Tabiiyki, xatoliklarni imkon qadar kamaytirish lozim. Statistik gipotezalarni tekshirish iloji boricha bir emas, bir necha marotaba takrorlanishi va ular asosida xulosaga kelinishi maqsadga muvofiqdir.
Statistik gipotezalarni tekshirish statistik ma‘lumotlarga asoslanadi. Faraz qilaylik, X 1 , X 2 , …, X n lar n – ta bog‗liqsiz tajribalardagi X t.m.ning kuzatilmalari bo‗lsin. X t.m.ning biron – bir xarakteristikasi haqidagi
asosiy H 0 gipoteza ko‘rilayotgan bo‗lsin. Endi statistik ma‘lumotlar asosida asosiy gipoteza H 0 ni qabul qilish yoki rad etish qoidasini tuzish kerak.
Asosiy gipoteza H 0 ni qabul qilish yoki rad etish qoidasi - H 0 gipotezani
tekshirishning statistik alomati deyiladi. Odatda statistik gipotezalarni tekshirish – statistik ma‘lumotlar asosida asosiy gipotezani tasdiqlash yoki uni rad etishdan iborat bo‗ladi. Endi statistik alomatlarni tuzish qoidalari bilan tanishamiz. Odatda statistik alomatni qurish empirik ma‘lumotarni asosiy H 0 gipoteza bo‗yicha tavsiflovchi statistika T = T ( X 1 , , X n ) ni
tanlashdan boshlanadi. Bunday tanlashda ikki xossa bajarilishi talab etiladi: a) statistika manfiy qiymatlar qabul qilmaydi; b) asosiy gipoteza to‗g‗ri bo‗lganda statistikaning aniq yoki gipotezaiy taqsimoti ma‘lum bo‗lishi kerak. Faraz qilaylik, bunday stastistika topilgan bo‗lib, S = { t: t = T ( X 1 , , X n ), X 1 , , X n – tanlanma fazosiga tegishli} - statistikaning
qiymatlar to‗plami bo‗lsin. Oldindan 0S 1 va S \ S 1 sohalarga ajratamizki, bunda asosiy gipoteza H 0 to‗g‗ri bo‗lganida T ( X 1 , , X n ) S 1 tasodifiy hodisaning ro‗y berish ehtimoli α dan oshmasin:
P T X 1 , H 0 .
, X n S 1
Asosiy gipoteza H 0 ni takshirish qoidasi quyidagicha bo‗ladi: x =( x 1 ,
… , x n ) t.m. X ning biror tanlanmasi qiymati bo‗lsin. Agar t = T ( x ) miqdor
soh a ga tegi s h li b o ‗ l s a : T ( x ) S 1 , u hol d a a s o s iy gi p o te z a H 0 to ‗ g ‗ r i
S 1
bo‗lganida rad etiladi. Aks holda, ya‘ni T ( x ) S 1 bo‗lsa asosiy gipoteza H 0 ni qabul qilishga asos bo‗ladi, chunki statistik ma‘lumotlar asosida qilingan hulosalar asosiy gipotezani rad etmaydi. Shuni ta‘kidlash lozimki, t S \ S 1 bo‗lishi asosiy gipoteza H 0 ni albatta to‗g‗ri bo‗lishini tasdiqlamaydi, balki bu holat statistik ma‘lumotlar va nazariy gipotezaning yetarli darajada
muvofiqligini
ko‗rsatadi
x a l o s . Yu q o r i d a k el tir i l g a n q o i d a da s tatist i k a l o m a t s tatist i k a s i, - s oha
T=T ( X 1 , , X n ) statistikani
S 1
alomatning kritik sohasi deyiladi. Odatda α ning qiymatlari uchun 0.1; 0.05; 0.01 sonlari qabul qilinadi. Yuqorida keltirilgan qoidadan shu kelib chiqadiki, alomatning kritik sohasi asosiy gipoteza H 0 to‗g‗ri bo‗lganida alomat statistikasining barcha kichik ehtimolli qiymalari to‗plamini o‗z
ichiga olishi lozim. Odatda kritik sohalar t t yoki t t ko‗rinishida
bo‗ladi.
Asosiy gipoteza H 0 ni tekshirish uchun yuqorida keltirilgan qoidaga asoslanganimizda biz ikki turdagi xatolikka yo‗l qo‗yishimiz mumkin: aslida to‗g‗ri bo‗lgan asosiy gipoteza H 0 ni rad etishimiz mumkin, ya‘ni H 0
to‗g‗ri bo‗lganida hodisasi ro‗y beradi. Bunday xatolik birinchi
t S 1
turdagi xatolik deyiladi. Demak, shartga asosan birinchi turdagi xatolik α dan oshmaydi. Ammo aslida noto‗g‗ri bo‗lgan asosiy gipoteza H 0 ni qabul qilishimiz, ya‘ni H 0 noto‗g‗ri bo‗lganida t T ( x ) S \ S 1 bo‗lib biz H 0 ni qabul qilishimiz mumkin. Bunday xatolik ikkinchi turdagi xatolik deyiladi.
Statistik alomatlarga qo‗yiladigan asosiy talablardan biri bu ikki turdagi xatoliklarni iloji boricha kichik bo‗lishini ta‘minlamog‗i kerak.
Demak, asosiy gipoteza H 0 ni tekshirish uchun turli statistikalarga
asoslangan statistik alomatlarni tuzish mumkin ekan. Tabiiyki, bunda statistik alomatlarni solishtirish masalasi kelib chiqadi.
Faraz qilaylik, alomatning kritik sohasi bo‗lsin. U holda H
S 1
gipoteza to‗g‗ri bo‗lganida statistikaning qiymati kritik sohaga tegishli bo‗lish ehtimolligi
W H P T X 1 , ... , X n S 1 H
alomatning quvvat funksiyasi deyiladi. Alomat quvvati H=H 1 bo‗lganida, ya‘ni W ( H 1 ) ehtimollik asosiy gipoteza noto‗g‗ri bo‗lganida to‗g‗ri yechimni qabul qilishi ehtimolligini anglatadi. Alomatning siljimaganlik xossasi muhim o‗rin tutadi va bu xossa
P T ( X 1 ,... , X n ) S 1 H 1
tengsizlik bilan aniqlanadi.
Asosiy gipoteza H 0 ni tekshirish uchun qiymatdorlik darajasi α
bo‗lgan ikkita S va S - alomat to‗plamlari aniqlangan bo‗lsin. Mavjud
*
1 1
statistik gipotezalarni ikki guruhga ajratish mumkin: parametrik va noparametrik gipoteza. T.m.larning taqsimot funksiyasi paramerli taqsimotlar oilasiga tegishli bo‗lsin. Ammo, taqsimotning parametrlari
( 1 ,..., n ) noma‘lumdir. Masalan, t.m. normal qonunlar oilasiga tegishli
bo‗lsa, uning taqsimot funksiyasi ikkita: o‗rta qiymat va dispersiya orqali to‗liq aniqlanadi va H 0 gipoteza, bu holda matematik kutilma hamda dispersiya qiymatlari haqida bo‗ladi. Demak H 0 gipoteza asosiy noma‘lum parametr qiymatlari haqida bo‗lar ekan. Bunday statistik gipotezaga parametrik gipoteza deb ataladi.
Agarda t.m.ning taqsimot funksiyasi umuman noma‘lum bo‗lsa, noparametrik gipoteza qabul qilinadi. Noparametrik gipoteza taqsimot funksiyasining ma‘lum xossalarga ega ekanligi haqida bo‗lishi mumkin.
Endi parametrik statistik alomatlarini qaraylik. X t.m.ning asl taqsimot funksiyasi quyidagi taqsimotlar oilasiga tegishli bo‗lsin:
F = F x , ,
Bu yerda θ =( θ 1 , …, θ r ) – r - o‗lchovli vektor, R r parametrlar qiy m a ti t o ‗ pla m i b o‗ lsin . U h o l da a s o s iy g i p o te z a H 0 ga a s o s a n 0 , alternativ gipotezaga asosan esa 1 \ 0 . Asosiy gipoteza H 0 ni
tekshirish uchun S va S ikkita kritik to‗plamlar bo‗lib, ular har birining
*
1 1
qiymatdorlik darajasi α bo‗lsin. Faraz qilaylik,
W S , W S , ,
( 8 .1.1)
*
1
1
0
va
W S , W S
, , (8.1. 2 )
*
1 1 1
bo‗lsin.
Aytaylik, (8.1.2) tengsizlikda hech bo‗lmaganda θ ning bitta qiymati
uchun qat‘iy tengsizlik o‗rinli bo‗lsin. U holda S ga asoslangan statistik
*
1
alomat nikiga nisbatan tekis quvvatliroq deyiladi. Tabiiyki, bu holda
S 1
S *
nikiga afzal ko‗rmoq maqsadga
ga a s o s lan g a n s ta ti s tik a l o m a t n i S
1 1
muvofiq bo‗ladi, chunki u alomat kam xatolikka yo‗l qo‗yadi.
Agarda (8.1.1) va (8.1.2) munosabatlar ixtiyoriy uchun o‗rinli
S 1
bo‗lsalar, S ga mos alomat tekis eng quvvatli (t.e.q.) alomat deyiladi.
*
1
8.2 Parametrik statistik alomat tuzish usullari
Oldingi paragrafda biz tekis eng quvvatli alomat haqida so‗z yuritdik. Tabiiyki t. e. q. alomat har doim mavjud bo‗lavermaydi. Endi parametrik statistik alomatlar orasida bo‗ladigan holni ko‗raylik. Faraz qilamiz, parametlar to‗plam Θ ikki elementdan iborat bo‗lsin: Θ = { θ 1 , θ 2 }. Asosiy gipoteza H 0 ga asosan θ=θ 0 bo‗lsin. U holda alternativ H 1 gipotezaga ko‗ra esa θ = θ 1 bo‗ladi.
Demak, shartga binoan biz o‗rganayotgan X t.m. H 0 gipotezaga a s o s a n F 0 x F x , 0 taq s i m ot g a , am m o H 1 raqob a tl a s h u v c hi g ipot ez a ga
k o ‗ ra e s a F 1 x F x , 1 taq s i m otiga e ga b o ‗ l a di. H a j m i n – ga teng b o ‗ l g a n ( X 1 , X 2 , ..., X n ) tanlanma asosida qaysi gipoteza to‗g‗ri ekanini aniqlash
 θ 0 bo‗lsin. Demak, ( x 0 ) ( x 1 ) 2 1 1 f x e , f ( x ) e 2 2 2 2 0 1 2 2 2 Endi haqiqatga o‗xshashlik statistik nisbati l ( x ) ni topaylik n n x x i exp n 2 2 1 0 x 2 2 2 2 l ( x ) exp 0 i 1 0 1 1 2 2 2 i 1 " width="640"
θ 0 bo‗lsin. Demak, ( x 0 ) ( x 1 ) 2 1 1 f x e , f ( x ) e 2 2 2 2 0 1 2 2 2 Endi haqiqatga o‗xshashlik statistik nisbati l ( x ) ni topaylik n n x x i exp n 2 2 1 0 x 2 2 2 2 l ( x ) exp 0 i 1 0 1 1 2 2 2 i 1 " width="640"
kerak. Bu statistik masala Yu. Neyman va E. Pirsonlar tomonidan hal qilingan.
Faraz qilaylik, F 0 ( x ) va F 1 ( x ) taqsimot funksiyalar absolut uzluksiz
taqsimot funksiyalar bo‗lib, mos ravishda f 0 ( x ) va f 1 ( x ) lar ularning zichlik funksiyalari bo‗lsin. Quyidagi nisbatni ko‗raylik
n
f 1 x i
l ( x ) i 1
f 0 x i
i 1
n
Mana shunday aniqlangan l ( x ) – haqiqatga o‗xshashlik nisbati deyiladi. Bu funksiya bilan bo‗g‗liq
c P l ( x ) c H 0
ehtimollikni kiritamiz. Bu yerda с – soni Ψ ( c ) = α tenglama bilan aniqlanadi.
Teorema(Neyman – Pirson). Yuqorida keltirilgan shartlar
bajarilganda har doim tekis eng quvvatli alomat mavjud va u quyidagi kritik to‗plam bilan aniqlanadi
S *
x : l ( x ) c .
1
Bu yerda c- kritik nuqta Ψ ( c ) = α tenglamadan topiladi.
T. e. q. alomat taqsimoti funksiyasi absolyut uzluksiz bo‗lgan hol uchun keltirildi. Ammo bunday alomat diskret taqsimotlar uchun ham mavjud bo‗ladi.
8.2 – misol. X 1 , X 2 , ..., X n lar noma‘lum θ o‗rta qiymatli va ma‘lum σ 2 dispersiyali normal taqsimlangan t.m.ning bog‗liqsiz tajribalar natijasida olingan kuzatilmalari bo‗lsin. Asosiy gipotezaga ko‗ra H 0 : θ = θ 0 , raqobatlashuvchi gipoteza H 1 ga ko‗ra θ = θ 1 va θ 1 θ 0 bo‗lsin. Demak,
( x 0 )
( x 1 ) 2
1
1
f x e
,
f ( x )
e
2 2
2 2
0
1
2 2 2
Endi haqiqatga o‗xshashlik statistik nisbati l ( x ) ni topaylik
n
n
x x i exp
n
2 2
1
0 x
2 2
2 2
l ( x ) exp
0
i 1 0
1
1
2
2
2
i 1
U holda l ( x ) c tengsizlik quyidagi
x 2 l n c n 2
1 0 1 0
tengsizlikka ekvivalent. Oxirgi tengsizlikni quyidagicha yozish mumkin.
l n c n t ( c )
n x
n
0
1 0
2
1 0
x - tanlanma o‗rta qiymat θ 0 va 2 n - parametrlik normal qonun bo‗yicha taqsimlangani uchun
( c ) P l ( x ) c H P n x t ( c ) t ( c )
0
0
Bu yerda ( x ) - Laplas funksiyasi. Tanlangan ixtiyoriy 0;1 ehtimollik u c hun, t c t , t ten g li k lar b a jari l a di g a n c α s oni h a r doim mavjud. Demak, Neyman – Pirson teoremasining barcha shartlari qanoatlantiriladi. Shu teoremaga asosan t. e. q. alomat mavjud va uning kritik to‗plami quyidagicha aniqlanadi.
x :
S *
n x t ,
- t
1
0
Mana shu alomatning quvvatini hisoblaylik. Alternativ H 1 gipotezaga ko‗ra x - tanlanmaning o‗rta qiymati θ 1 va 2 n - parametrli normal qonun bo‗yicha taqsimlangandir. U holda
n
n
x
t H 1
W ( S , ) P x t H P
n
*
1 1 0 1
1 0
1
(8.2.1)
n
t
0
1
( 8.2. 1 ) m uno s a b a td a n ikk i n c hi t ur x a to l ik , n t n 1 0
ekanligi kelib chiqadi.
Endi quyidagi masalani ko‗raylik. Aliomatning qiymatdorlik darajasi
α ga teng bo‗lganida, ikkinchi tur xatolik β ga teng bo‗lishi uchun nechta
ku za til m a k e ra k ? ; ya ‘ n i tanl a n m a ni n g h a j m i q a nd a y b o ‗ l i s hi k e ra k ? Kerakli n soni topish uchun ikkita tenglamaga egamiz. Bular
t v a t n 1 0
(8.2. 2 )
Φ ( y )= p tenglamaning yechimini ko‗raylik. Bu tenglamaning yechimi y p
normal qonunning p – chi kvantili deyiladi. U holda (8.2.2) ga asosan
2
2 y y
t n 1 0 y . Ox i r g i ikki ten g l ikdan n
1
- t y ,
2
1 0
munosabatga ega bo‗lamiz. Qidirayotgan son butun bo‗lishi lozim.
2
2 y y
1 . Bu erda [ a ] – a sonning butun
Shuning uchun,
n *
2
1 0
qismi. Masalan, α=β =0.05 va 1 0 0.1 bo‗lsa, u holda n * =1076 bo‗ladi;
agarda α = β =0.001, 1 0 1 bo‗lsa, n * =39 bo‗ladi.
8.3 Noparametrik muvofiqlik alomatlari
Faraz qilaylik, X 1 ,X 2 , ..., X n lar bog‗liqsiz n ta tajriba natijasida X t.m.ning olingan kutilmalari bo‗lsin. X t.m.ning taqsimoti noma‘lum F ( x ) funksiyadan iborat bo‗lsin. Noparametrik asosiy gipotezaga ko‗ra H 0 : F ( x )= F 0 ( x ). Mana shu statistik gipotezani tekshirish talab etilsin.
1. A. Kolmogorovning muvofiqlik alomati
X 1 ,X 2 , ..., X n kuzatilmalar asosida F n ( x ) empirik taqsimot funksiyasini tuzamiz. Faraz qilamiz, F ( x ) uzluksiz taqsimot funksiyasi bo‗lsin. Quyidagi statistikani kiritamiz
D n D n X 1 , X 2 , ... , X n s u p
x
F n ( x ) F ( x )
Glivenko teoremasiga ko‗ra n yetarli katta bo‗lganda D n kichik qiymat qabul qiladi. Demak, agar asosiy gipoteza H 0 o‗rinli bo‗lsa D n statistika kichik bo‗lishi kerak. Kolmogorovning muvofiqlik alomati D n statistikaning shu xossasiga asoslangandir.
Teorema(Kolmogorov). Ixtiyoriy uzluksiz F ( x ) taqsimot funksiyasi va λ uchun
l im P n D K ( )
2 2
( 1) i e 2 i
n
n
i
bo‗ladi.
D n – statistikaga asoslangan statistik alomat kritik to‗plami quyidagicha aniqlanadi
S 1 t : t D n ( x 1 , x 2 ,... , x n ) t .
Bu yerdan 0α
Kolmogorov teoremasidan quyidagi xulosalar kelib chiqadi:
a) D n – statistikaning H 0 gipoteza to‗g‗ri bo‗lgandagi taqsimoti F ( x ) bog‗liq emas;
b ) A m a liy nuqt a y i n aza r d a n n ≥ 20 b o ‗ l g a nd ay oq t e ore m a d a gi
ya qi n las h i sh juda ya xshi n a t i ja b e ra d i, ya ‘ n i P n D n ni K( λ ) bil a n almashtirishdan yo‗l qo‗yiladigan xatolik yetarlicha kichikdir.
Bu xulosalardan kelib chiqadiki, n ≥ 20 bo‗lsa kritik chegara t α ni
n ga teng deb olish mumkin. Bu yerda λ α K (λ α ) = 1- α tenglamaning
ildizlaridan iborat. Haqiqatan ham berilgan 0
P D n S 1 H 0 P n D n H 0 1 K ( ) .
Shunday qilib, Kolmogorov alomati quyidagicha aniqlanadi:
- berilgan α orqali K( λ α ) = 1- α tenglama yechimi λ α jadval yordamida topiladi.
- berilgan tajriba natijalari x 1 , x 2 , …, x n larga ko‗ra t = D n ( x 1 , x 2 , …, x n )
qiymati hisoblanadi,
3) nt va λ α solishtiriladi, agar nt bo‗lsa asosiy gipoteza H 0 rad eriladi, aks holda tajriba H 0 ni tasdiqlaydi.
2. K. Pirsonning xi–kvadrat muvofiqlik alomati
Amaliyotda Kolmogorov statistikasini hisoblash ancha murakkab va undan tashqari Kolmogorov alomatini qo‗llash faqat taqsimot funksiya F ( x ) uzluksiz bo‗lgandagina mimkindir. Shuning uchun, amaliyotda ko‗p hollarda Pirsonning xi – kvadrat alomati qo‗llaniladi. Bu alomat universal xarakterga ega bo‗lib, kuzatilmalarni guruhlash usuliga asoslangandir.
Faraz qilaylik, X – kuzatilayotgan va taqsimot funksiyasi noma‘lum
F ( x ) bo‗lgan X t.m.ning qiymatlari to‗plami bo‗lsin. X ni k ta kesishmaydigan oraliqlarga ajratamiz:
k
X i , i ∩ j 0 , i j , i , j 1 , 2 ,.. . , k
i 1
Takrorlanishlar vektori deb ataladigan ( 1 ,..., k ) vektorni olaylik.
i o raliqqa vektori
Bu vektorning i – koordinatasi kuzatilmalardan i tasi
tushganligini anglatadi. Ko‗rinib turibdiki, takrorlanishlar
tanlanma ( X 1 , , X n ) orqali bir qiymatli aniqlanadi va 1 2 ... k n . Asosiy gipoteza H 0 to‗g‗ri, bo‗lgandagi kuzatilmaning i oraliqqa tushish, ehtimolligini P i 0 bilan belgilaylik:
P i 0 P X i
Quyidagi statistikani kiritamiz
k
H 0 , i 1 , 2 ,... , k .
2
- nP
n
i 1
k
i 0
2
nP
i 0
va H 0 : F ( x ) F 0 ( x ) a s o s iy gi p otez a ni to ‗ g ‗ r il i gini t e k s h i r a m iz.
Kuchaytirilgan katta sonlar qonuniga asosan nisbiy chastota r n bir
intiladi. Demak, agar H 0
e hti m ollik b i lan naza r i y e hti m ollik ga
P r 0
2
gipoteza o‗rinli bo‗lsa, u holda
statistikaning qiymati yetarli darajada
n
kichik bo‗lishi kerak.Demak, Pirsonning mezoni statistikaning katta
2 2
n
qiymatlarida asosiy gipoteza H 0 ni rad etadi, ya‘ni alomatning kritik sohasi
S ko‗rinishda bo‗ladi. Asosiy gipoteza H to‗g‗ri bo‗lganida
2
t : t t
0
1
n
statistikaning aniq taqsimotini hisoblash ancha murakkab, bu esa o‗z navbatida alomatning kritik chegarasi t ni topishda qiyinchilik tug‗diradi.
2
Am m o, n ye tar l i k a tta b o ‗ l sa H 0 gipot ez a to ‗g‗ ri b o ‗ l g a n i da statistikaning taqsimotini limit taqsimot bilan almashtirish mumkin.
Teorema(Pirson). Agar 0P i 0 i 1,2,..., k . bo‗lsa, u holda
n
t .
t H P
2
2
l i m P
0
n
k 1
n
erkinlik darajasi k-1 bo‗lgan xi – kvadrat taqsimotiga ega
Bu yerda
2
k 1
bo‗lgan t.m.dir:
- x
t
1
P
k 1
x 2
2
k 1
t
e 2 dx
,
k 1
k 1
0
2 2
2

n - Gamma funksiya. ■
Amaliyotda bu teorema natijasidan n≥50, i 45 , i 1,2,..., k . bo‗lganda
P t , 0 1
foydalanish mumkin. Bu holda t
2
k 1
tenglamadan topiladi.
8.4 Matematik kutilma va dispersiyalar haqidagi statistik gipotezalarni tekshirish
Ikki bosh to‗plamlar matematik kutilmalari va dispersiyalarining tengligini tekshirish masalalariini ko‗raylik. Ikkala bosh to‗plam normal taqsimlangan deb faraz qilamiz. Demak, birinchi bosh to‗plamdan X (n) =( X 1 ,
… , X n ) , ikkinchi bosh to‗plamdan esa Y (m) =( Y 1 , …, Y m ) tanlanmalari olingan bo‗lsin.
1. Matematik kutilmalar noma’lum bo‘lganida dispersiyalar tengligi haqidagi gipotezani tekshirish
X , X , …, X lar o‗rta qiymati noma‘lum va dispersiyasi bo‗lgan
2
x
1 2 n
normal taqsimlangan X t.m. kuzatilmalari va Y 1 , Y 2 , …, Y m lar esa o‗rta
bo‗lgan normal taqsimlangan
qiy m a ti nom a ‘ l um va di s p e rsi ya si
2
y
tas diqdan,
t.m.ning kuzatilmalari bo‗lsin. Asosiy gipoteza H : =
2
x y
0
alternativ gipoteza H : ≠ tasdiqdan iborat bo‗lsin. Dispersiyalarining
2
y
2
1
x
eng yaxshi statistik baholarini ko‗raylik:
1
m 1
1
n 1
X x 2 va
y
n
m
2
2
2
i
Y y
x
i
i 1
i 1
F – statistika deb ataluvchi quyidagi statistikani kiritamiz
1 X
n
x 2
2
i
x n 1
i 1
F
1
m 1
m
2
y
2
Y y
i
i 1
Teorema(Snedekor). Agarda X o‗rta qiymati θ va dispersiyasi
2
x
1
bo‗lgan normal qonun bo‗yicha taqsimlangan t.m. va Y o‗rta qiymati θ 2 va

disp er siy a s i
bo‗lsa, u holda
bo‗lgan normal qonun bo‗yicha taqsimlangan t.m.lar
2
y
2
x
2
y
2
y
2
x
t.m. erkinlik darajalari n -1 va m -1 bo‗lgan Snedekor taqsimotiga ega bo‗ladi. ■
Snedekor taqsimotining zichlik funksiyasi
n m
n
n
x 2
1
2
f x n 2
, x 0
m
n , m
n m
1 n x m n m
2
2 2
formula bilan aniqlanadi.
Alomatning kritik sohasi quyidagicha tiziladi. Agarda
2
2
yoki x
( C 1 C 2 )
x C
- C
2
2 1 2
y y
bo‗lsa, asosiy gipoteza H 0 ni rad etmoq lozim.
Yuqorida keltirilgan Snedekor teoremasidan foydalanib C 1 va C 2 – sonlarni aniqlaylik. Jadvaldan erkinlik darajasiga asosan Snedekor taqsimotining 1-α kvantili topiladi. Masalan, α = 0.15 va n = m = 9 bo‗lsa
1
C 1 = 3.44, C 0.29 .
1
C
2
2. Mat e m at i k kut i l m al a r m a’ l um b o ‘l g a n i d a d i sp er s i y a l a r tengligi haqidagi gipotezani tekshirish
2
Bu gipoteza oldingi gipotezaga o‗xshash tekshiriladi. Ammo x va
2
y dispersiyalar mos ravishda quyidagicha hisoblanadi:
1
n
X
1
m
,
2
2
i 1
2
i 1
2
Y
,
x
y
i x
i y
n 1
m 1
B u ye r d a x va y lar X va Y t .m .l a r o ‗ rta q i y m a t lari d i r .
3. Dispersiyalar noma’lum bo‘lganida matematik kutilmalar tengligi haqidagi gipotezani tekshirish
Faraz qilaylik, X va Y t.m.lar mos ravishda o‗rta qiymatlari x va y ,
dispersiyalari bo‗lgan normal qonun bo‗yicha taqsimlangan
2 2 2
x y
bo‗lib, 2 , va lar noma‘lum bo‗lsin. ( X , …, X ) X t.m.ning
x y 1 n
tanlanmasi va ( Y 1 , …, Y m ) – Y t.m.ning tanlanmasi bo‗lsin. Asosiy gipoteza
H 0 : x = y va alternativ gipoteza H 1 : x ≠ y lardan biri o‗rinli ekanini
tekshirish kerak. Tanlanmalar o‗rta qiymatlari ayirmasi x y ni qaraylik. Shartga ko‗ra
D x y 2 n m .
n m
Quyidagi statistikani kiritamiz:
n m
x y
t
n m
2
2
y n m 2
n 1 m 1
x
Bu statistika erkinlik darajasi n + m – 2 bo‗lgan Styudent taqsimotiga ega bo‗ladi. U holda asosiy gipoteza H 0 o‗rinli bo‗lishini tekshiruvchi statistik
t t n m 2 b o ‗ l sa g i pote z a H 0
a l o m a t qu y i d a gicha t u z il a di: a g ar da
t n m 2
gipoteza rad etiladi. Bu yerda
qiymatdorlik darajasi α –
bo‗lgan Styudent taqsimotining kritik nuqtasidir.
4. Di sp er siya l ar m a’ l u m bolgani d a o ‘ r ta q i y m at l a r ten gl i gi haqidagi gipotezani tekshirish
E ndi o ‗ r ta qiy m a t lar ten g l i g i h a q ida gi g i pote z a ni d isp er siy a lar ma‘lum bo‗lganida tekshiruvchi alomat ko‗rib o‗tamiz. Bu holda
x y
t
2
y
2
x
n m
t.m. standart normal qonunga ega. Shuning uchun agarda t U bo‗lsa H 0
: x = y asosiy gipoteza rad etiladi. Bu yerda U α – qiymatdorlik darajasi α
(0α

VIII bobga doir misollar
- Telefon stansiyasida har minutda noto‗g‗ri ulanishlar soni X ustida kuzatishlar olib borilib 1 soat davomida quyidagi ma‘lumotlar olindi: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; 4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5. Bu tanlamaning nazariy taqsimoti Puasson taqsimotidan iboratligi haqidagi H gipotezani tekshiring( α =0.05).
- Ma‘lum mahsulotning narxi X ning dispersiyasi 2 2.25 ga teng va quyidagi statistik tanlanmaga ega:
Narxlar I n te r v a li
Chastotasi
3.0-3.6
3.6-4.2
2
4.2-4.8
8
4.8-5.4
35
5.4-6.0
43
6.0-6.6
22
6.6-7.2
15
5
Xi -kvadrat alomat yordamida bu tanlanmaning 99% ishonch bilan
normal taqsimotga ega ekanligi haqidagi H gipoteza o‗rinli
N ( 5 ; 2 . 2 5 )
bo‗lishini tekshiring.
3. Byuffon tangani n=4040 marta tashlaganida gerb tomoni m=2048 marta tushgan. Bu tajriba natijanlari tanga simmetrikligi haqidagi H gipoteza bilan muvofiq keladimi? Bunda α =0.05 va α =0.1 bo‗lgan hollarni ko‗ring.
IX bob. Ko‘p o‘lchovli statistik tahlil usullari
Ko‗p sondagi korrelatsiyalangan miqdorlardan, yangi oz sondagi korrelatsiyalanmagan miqdorlarga o‗tish ko‗p o‗lchovli statistik tahlilning mohiyatini tashkil qiladi.
9.1 Faktorli tahlil
Iqtisodiy ko‗rsatkichlarning o‗zgarishini belgilovchi va iqtisodiy obyektlarni tasniflashni o‗rganuvchi ― yashirin‖ faktorlarni aniqlash va ularni tahlil qilish ko‗p o‗lchovli statistik tahlilni asosiy masalalaridir.
Iqtisodiy ko‗rsatkichlar o‗zgarishini belgilovchi omillar to‗plami komponentalari orasida stoxastik bog‗lanishlar bo‗lgan ko‗p o‗lchovli vektor sifatida hamda ―yashirin‖ faktorlar esa markazlashtirilgan va korrelatsiyalanmagan t.m.lar deb qaraladi. Mana shunday ―yashirin‖ faktorlarni aniqlash faktorli tahlilning, xususan, bosh komponentalar usulining asosiy masalalarini tashkil qiladi.
Iqtisodiy obyektlarni tasniflashda ko‗p o‗lchovli tanlanma iqtisodiy omillar qiymatlaridan tuziladi. Har bir ko‗p o‗lchovli tanlanma – ko‗p o‗lchovli t.m.ning amalga olingan qiymatlaridan iborat bo‗lib, u
o‗rganilayotgan iqtisodiy ob‘ektni tavsiflashga, sinflarga ajratishga xizmat qiladi. Shu maqsad yo‗lida ko‗p o‗lchovli t.m.ning taqsimot funksiyasi
haqida oldindan ma‘lumotga ega bo‗lish muhimdir. Agar mana shunday
ma‘lumot bo‗lmasa, sinflarga ajratish ularni tashkil qiluvchi obyektlar
― yaqinligi‖ asosida amalga oshiriladi; bunda bir sinfdagi obyektlar
― yaqin‖, turli sinfdagilari esa bir – birlaridan ―uzoq‖ da bo‗ladilar. Obyektlar orasidagi ―yaqinlik‖ ni belgilovchi masofa turlicha aniqlanishi mumkin, xususan, n o‗lchovli Yevklid fazosidagi masofa deb ham aniqlanishi mumkin.
Endi faktorli tahlil usuliga o‗taylik. Quyidagi holatni o‗rganaylik. Aniq bir shaxsga yakka holda kiyim tikish lozim. Buning uchun shu yakka
shaxsni qaddi – qomatini tavsiflaydigan bir nechta ma‘lumotlar yig‗iladi. Shu kiyim sanoat korxonasida ishlab chiqilsa faqat uchta o‗zaro bog‗liq
ma‘lumotlarga asoslanadi xolos: o‗lcham, bo‗y va to‗lalik. Bu holat
faktorli tahlilning asosiy masalasini to‗liq namoyish qiladi: boshlang‗ich ko‗p sondagi o‗zaro bog‗langan F 1 , …, F k, k t ―yashirin‖ omillarga o‗tish masalasi.
Iqtisodiyotda shu turdagi masalalar ko‗plab uchraydi. Masalan, ishlab chiqarish manbalaridan samarali foydalanish uchun bir necha umumlashtiruvchi ko‗rsatkichlarni topish zarurati tug‗iladi.
Faktorli tahlil modeli quyidagi ko‗rinishda bo‗ladi:
X i a i a ij F j v i i ,
j 1
n
i = 1, 2, … , m , k m ( 9 . 1.1)
Bu yerda MX i a i , F j , j = 1, 2, …, k – umumiy (―yashirin‖) faktorlar;
- b o s h la n g ‗ ich k o ‗ r s a t k ic h lar n in g u m u m iy faktorlariga ta‘s i r
a ij
koeffitsentlari;
i , i 1 , 2 ,... , m - m a x s u s f a k t o r lar ;
i - k o ‗ r s a tki c hlar n ing m a xsus f a k t o r lar g a t a ‘ s i r i.
U m u m iy va m a x s u s faktorlar m a r k az l a s hti r ilg a n ( M F j 0 , j 1 , 2 ,. . . , k ,
), normallangan ( MF 1, j 1,2,..., k , ) va
M 0 , i 1 , 2 ,... , m
M 1 , i 1 , 2 ,.. . , m
2
2
i
i
j
ko r rel y a t siy a la n m a g a n ( M F j F j 0 , j j , M F j j 0 ,
M i i 0 , i i ,
j , j 1,2,... k , i , i 1,2,..., m ) deb faraz qilamiz.
Faktorli tahlilning (9.1.1) modeli matritsalar yordamida quyidagicha yoziladi
X a A F V , ( 9 . 1.2)
X 1 a 1
, a ⁝ - boshlang‗ich ko‗rsatkichlar va ularning
bu yerda X ⁝
X
a
m m
matematik kutilmalaridan tuzilgan vektor ustun.
F 1 1
F ⁝ , ⁝ - umumiy va maxsus faktorlar vektor ustuni.
F
m
k
0 …
0 v … 0
⁝ ⁝⁝⁝
0 0 … v
…
a a … a
⁝ ⁝⁝⁝ ⁝
a a … a
0
v 1
a 1 k
a 11 a 12
-
2
V
21
2 k
22
,
A
⁝
⁝
⁝
m
m 1 m 2 m k
umumiy va maxsus faktorlar ta‘sir koeffitsientlari matritsalari.
( 9 . 1. 2 ) ga a s o s a n X k o ‗ p o‗ l c ho v li k o ‗ r s a tki c h u c hta korrelatsiyalanmagan tarkibiy qo‗shiluvchilardan iborat ekan:
- a - tasodifiy bo‗lmagan tarkibiy bo‗lak (matematik kutilma);
- umumiy faktorlar aniqlaydigan AF – tasodifiy tarkibiy bo‗lak;
- maxsus faktorlar aniqlaydigan V ε tasodifiy tarkibiy bo‗lak.
Faktorli tahlilning (9.1.2) modelini amalga oshirish (qo‗llash) uchun hech bo‗lmaganda uning birinchi ikki tarkibiy qoshiluvchilarini statistik ma‘lumotlar asosida statistik baholash lozim. Bulardan, birinchisi matematik kutilma a ni tanlanmaning o‗rta qiymati a ga, ikkinchi qo‗shiluvchini ularning statistik baholariga, ya‘ni umumiy faktorlar ta‘sir koeffitsientlari bahosi va umumiy faktorlar bahosiga almashtirish kerak.
Yuqoridagi masalalarni yechish uchun bir necha usullar mavjud. Ana shulardan biri – bosh komponentalar usulidir.
9.2 Bosh komponentalar usuli
Bosh komponentalar usulu (ingl. Principal component analysis, PCA) — olingan ma‘lumotlarni eng kam informatsiya yo‗qotgan holda o‗lchovini pasaytirishning asosiy usullaridan biri hisoblanadi. U K. Pirson tomonidan 1901 yilda taklif etilgan bo‗lib, ko‗pgina amaliy masalalarni echishda keng qo‗llaniladi. Bosh komponentalarni hisoblash boshlang‗ich ma‘lumotdan tuzilgan kovariatsion matrisaning hos son va hos vectorlarni hisoblashga keltiriladi.
Bosh komponentalar usuli butun to‗lig‗icha umumiy ko‗rsatkichlarga asoslanib hulosa chiqaradi. Bu usulda ham faktorlar markazlashtirilgan, normallangan va korrelatsiyalanmagandir.
- O‘rganilayotgan X ko‘rsatkichlar sistemasining birinchi bosh komponentasi Y 1 ( X ) ushbu ko‘rshatkichlardan tuzilgan normallashgan, markazlashtirilgan shunday chiziqli kombinatsiyasiki, u qolgan barcha shunday chiziqli kombinatsiyalar orasida eng katta dispersiyaga ega bo‗lishi kerak.
- O‘rganilayotgan X ko‘rsatkichlar sistemasining k -bosh komponentasi Y 1 ( X ) ushbu ko‘rshatkichlardan tuzilgan normallashgan, markazlashtirilgan shunday chiziqli kombinatsiyasiki, u oldingi k -1 bosh komponentalar bilan korrelyatsiyalanmagan va qolgan barcha normallashgan, markazlashtirilgan va korrelyatsiyalanmagan oldingi k -1 chiziqli kombinatsiyalar orasida eng katta dispersiyaga egadir.

Uning mohiyati quyidagicha. Ushbu
X i a i a j F j ,
j 1
m
(9.2. 1 )
i 1 , 2 ,. . . , m
yoki matritsa ko‗rinishida yozib oladigan bo‗lsak,
X a AF
ifodani ko‗raylik. Markazlashtirilgan boshlang‗ich ko‗rsatkichlarni
Y j X j a j , deb belgilaylik. U holda (9.2.1) munosabatni
j 1 , 2 ,... , m
(9.1.2) bilan solishtirish natijasida quyidagicha yozishimiz mumkin:
(9.2. 2 )
Y A F ,
A – faktorlar ta‘siri koeffitsienti matritsasini aniqlash maqsadida boshlang‗ich ko‗rsatkichlar kovariatsiyasi matritsasining xos sonlarini va xos vektorlarini l bilan belgilaylik:
B c o v x , x c o v ( y , y ) M Y Y .
i j i j
m m
Eslatib o‗tish joizki, xos sonlar quyidagi tenglamadan topiladi:
B l l y oki B E m l 0 .
(9.2. 3 )
Bu yerda E m – birlik matritsa. (9.2.3) bir jinsli tenglamalar sistemasi noldan farqli yechimga ega bo‗lishi uchun bosh determinanti nol bo‗lishi kerak
B E 0 (9.2.4)
(9.2.4) tenglama λ ga nisbatan m ta tenglamalardan iborat bo‗lib, B – matritsaning 1 ,..., m xos sonlaridan iborat bo‗lgan yechimlarga ega.
Turli xos sonlarga mos keluvchi xos vektorlar ortogonal, shuning uchun
L ( l 1 , . . . , l m )

matritsa normallangan xos vektorlardan tuzilgan bo‗lganligi uchun ham ortogonal matritsadir. Ortogonal matritsa koordinatalar o‗qini burishni anglatadi.
Shuning uchun, markazlashtirilgan boshlang‗ich ko‗rsatkichlarni ortogonal L matritsa yordamida chiziqli almashtirish koordinatalar o‗qini burishni anglatadi:
f L Y , Y Lf
(9.2.5)
Hosil bo‗lgan yangi ko‗rsatkichlar korrelatsiyalanmagan bo‗ladi. Haqiqatan ham, (9.2.5) ga asosan ko‗rsatkichlar markazlashtirilgan bo‗lgani uchun
c o v ( f i , f j ) M f f M L Y Y L L M Y Y L L B L
0
1
0
0
0
.
2
I I
I B I
j
i j
0
0
m
De m a k,
D f i c o v ( f i , f i ) i .
c o v ( f i , f j ) 0 , i j ,
Ortogonal almashtirish masofani saqlaydi, shu sababli
m m
i
i 1
2
2
Y f
.
i
i 1
dispersiyasi
Demak, boshlang‗ich ko‗rsatkichlarni barcha normallashmagan bosh komponentalar dispersiyasiga tengdir:
m m
2 2
n m
n
D X i M Y i M f i D f i i .
(9.2. 6 )
i 1 i 1
i 1
i 1
i 1
Oxirgi tenglikdan ko‗rinadiki, boshlang‗ich ko‗rsatkichlarning barcha dispersiyasi xos sonlar yig‗indisiga teng ekan. Bosh komponentalar usulida xos sonlar tartiblanadi 1 2 ... m .
Amaliyotda katta xos sonlarga mos keluvchi bir necha bosh komponentalar bilan ish ko‗riladi. Bunga asos bo‗lib (9.2.6) tenglik xizmat

qiladi, ya‘ni boshlang‗ich ko‗rsatkichlarning dispersiyasi shu xos sonlar yig‗indisiga juda yaqin bo‗ladi.
f i
Bosh komponentalarni normallashtiraylik F
y oki
F 1 2 f
i
i
-matritsa ko‗rinishida yozamiz. Bu yerda
1
0 … 0
1
1
.
… 0
0
1 2
⁝
0
2
⁝ ⁝⁝ ⁝ ⁝
1
0 …
m
E ndi f 1 2 F b o ‗ l g a n l i g i uc hun Y L f L 1 2 F A F .
Oxirgi tenglikdan boshlang‗ich ko‗rsatkichlarning umumiy faktorlarga ta‘siri
1 0 … 0
0 2 … 0
⁝ ⁝ ⁝⁝⁝ ⁝
0 0 …
(9.2. 7 )
A L 1 2 ,
1 2
m
ko‗rinishda ekanligi kelib chiqadi.
Amaliyotda yuqorida chiqarilgan xulosalar va bajarilgan hisoblarni nazariy matematik kutilma a va kovariatsiyalar matritsasi B uchun emas,
balki tanlanmalar yordamida ular uchun qurilgan a va B statistik baholar uchun bajarish kerak. Buni quyidagi misolda ko‘raylik.
9.1 – misol . 24 ta ( n =24) toshbaqalarning tosh pansirlari ko‘rsatkichlari: uzunligi X 1 , eni X 2 va balandligi X 3 ni (mm larda) o‘lchash natijasida quyidagi
kovariatsion matrisa B hosil qilingan bo‘lsin,
271.17 168.70
45 1 . 39
171.73 103.29 .
10 3 . 2 9 6 6 . 6 5
B € 27 1 . 17
168.70
(9.2.4)ga asosan quyidagi mos 3-darajali
168.70
1 0 3 . 2 9 0 .
6 6 . 6 5
451.39 271.17
2 7 1 . 1 7 1 7 1 . 7 3
168.70 103.29

tenglamani echib mos ravishda λ 1 =680.40, λ 2 =6.50 va λ 3 =2.86 ekanligini aniqlaymiz. Topilgan xos sonlarni mos ravishda (9.2.5) sistemaga qo‘yib, ularni noma‘lum l i ( l i 1 , l i 2 , l i 3 ) larga nisbatan hisoblaymiz:
0. 812 6 0. 545 4
0. 205 4
l 0.4955 , l 0.8321 , l
'
'
'
0. 249 1
3
2
1
0.1006 0.9465
0. 306 8
U holda bosh komponentalar quyidagiga teng bo‘ladi:
f (1 ) 0 . 8 1 X 1 0 . 5 0 X 2 0 . 3 1 X 3 ;
f ( 1 ) 0 . 5 5 X 1 0 . 8 3 X 2 0 . 1 0 X 3 ;
f ( 1 ) 0 . 2 1 X 1 0 . 2 5 X 2 0 . 9 5 X 3 .
IX bobga doir misollar
1. Tavakkaliga tanlangan 20 talabalarning vazni ( X ), yoshi (Y) va
bo‗yi (Z) to‗g‗risidagi ma‘lumotlar asosida tuzilgan quyidagi B kovariatsion matrisa uchun bosh komponentalarini hisoblang:
19.69 1.11 14.13
B € 1.11 2.09 1.33 .
14.13 1.33 17.61
2. Quyidagi kovariatsion matrisalar uchun
hamda bosh komponentalarini hisoblang.
3.74 1.85 2.12 2 6 .03 1 6 .50 1 6 .40
D f i c o v ( f i , f i ) i
lar n i
b) 16.50
6 4 .95 9. 5 6 .
a) 1.85 6.33 0.70 ;
2.12 0.70 2.00
1 6 .40 9. 5 6 1 9 .79
ILO V A
1-ilova
- x 2
1
( x ) e 2 funksiyaning qiymatlari jadvali
x
0,0
0
0,1
0,3989
1
2
3970
0,2
3989
2
0,3
3910
3965
3989
3814
3961
3
3902
0,4
3988
4
3894
0,5
3986
3683
3956
3802
3951
3790
5
3521
3668
0,6
3885
3984
6
3778
3503
0,7
3653
3945
3982
3332
3876
3123
3765
3485
7
3939
3312
3867
3637
0,8
3980
8
3467
3101
3292
3621
3977
3932
2897
3752
3857
0,9
9
3448
3079
3925
3739
3271
2661
1,0
2874
3973
3847
3605
2850
3918
3429
0,2420
3589
3251
3056
3836
3726
2637
1,1
3034
3712
3410
2827
2396
2613
2179
3572
3230
3825
1,2
3697
3011
1942
3555
3209
3391
2803
2371
1,3
2589
2155
2989
3327
3538
1,4
2780
2131
3187
2565
1919
1714
2347
3352
3166
2323
1895
2966
1497
2756
1691
2541
1,5
2107
2943
1,6
1295
2083
1669
1476
1872
3144
2299
2516
2732
1456
1849
2920
1109
2709
2275
1647
1,7
1276
2492
2059
1435
2685
1092
0940
1626
1257
1826
1,8
2251
2036
2468
2227
1074
1415
1804
0790
2012
2444
1238
0925
1604
1,9
1219
2,0
0656
1057
0775
0909
2203
1582
1781
1989
1394
1040
1758
1374
0761
0,0540
1561
1965
1200
2,1
0893
0644
0748
1736
0529
0878
0632
1539
1023
1182
2,2
1354
0440
0734
0355
0519
1006
1334
1163
0620
2,3
1518
0431
0863
0508
2,4
0283
0608
0347
0422
0721
0989
0848
1315
1145
0498
0224
0339
0707
0973
0413
2,5
1127
0596
0833
0277
0332
0175
2,6
0404
0219
0270
0957
0488
0584
0818
0694
0478
0136
0681
0325
0213
2,7
0396
0804
0573
0264
0171
0167
0104
0208
0132
0258
0669
0387
0562
0468
0317
2,8
0129
0459
0310
0203
0551
2,9
0079
0163
0379
0101
0252
0371
0060
0198
0099
0303
0126
0449
0158
0246
3,0
0077
0122
0297
0194
0058
0075
0241
0154
0,0044
3,1
0096
0363
0056
0093
0033
0151
0119
0290
0189
0235
0043
3,2
0073
0116
0184
0091
0055
3,3
0042
0147
0229
0071
0032
0024
0180
0017
0143
0031
0088
0113
0053
0040
0023
3,4
0069
0110
0051
0012
0022
0067
0139
0017
0039
0030
0086
3,5
0009
0016
0029
0050
0084
0107
0012
0038
3,6
0022
0065
0006
0048
0063
0021
0016
0081
3,7
0012
0028
0037
0008
0015
0008
0004
0047
0027
0020
0061
0006
0011
0036
3,8
0008
0035
0006
0004
0011
0015
0003
0020
0026
3,9
0046
0025
0004
0014
0002
0008
0005
0034
0019
0003
0010
0002
0004
0003
0005
0007
0010
0014
0025
0018
0007
0013
0002
0004
0010
0003
0005
0018
0013
0004
0003
0009
0002
0005
0007
0003
0007
0002
0002
0009
0005
0002
0006
0002
0005
0003
0002
0003
0002
0004
0003
0002
0002
0001
0002
0001
2-ilova
1
2
x
0
2
e t 2 d t f u n k s iy a ning qiy m a tl a ri j a dv a li
( x )
0
x
0,00
0 ( x )
0,0000
x
0,01
0 ( x )
0,0040
0,45
0,02
0,0080
0,1736
x
0,03
0,46
0,47
0,04
0,1772
0,0120
0 ( x )
0,90
0,0160
0,3159
0,1808
0,05
0,91
x
0,48
0,06
0,1844
0,49
0,0199
0,92
0,3186
1,35
0 ( x )
0,0239
0,3212
0,1879
0,4115
0,07
0,93
1,36
0,50
0,51
0,08
0,1915
0,4131
0,94
0,3238
1,37
0,0279
0,3264
0,0319
0,4147
0,1950
0,09
0,95
1,38
0,52
0,0359
0,10
0,53
0,1985
1,39
0,96
0,4162
0,3289
0,4177
0,3315
0,0398
0,2019
0,11
0,97
1,40
0,54
0,55
1,41
0,2054
0,0438
0,4192
0,98
0,3340
0,12
0,4207
0,3365
0,2088
0,0478
0,99
0,13
0,56
1,42
0,2123
0,0517
1,00
0,3389
1,43
0,4222
0,14
0,57
0,3413
0,4236
1,44
1,01
0,0557
0,58
0,15
0,2157
0,2190
0,0596
0,4251
1,45
0,3438
0,16
1,02
0,59
0,4265
0,60
0,2224
1,46
0,3465
0,0636
1,03
0,17
0,0675
0,3485
0,4279
0,2257
0,61
1,04
0,18
1,47
0,0714
0,62
0,4292
0,19
1,48
0,2291
1,05
0,3508
0,4306
0,0753
0,3531
0,2324
1,49
1,06
0,20
0,63
0,64
0,2357
0,0793
0,21
0,3554
1,07
0,4319
1,50
0,0832
0,3577
0,4332
0,2389
0,65
1,08
1,51
0,22
0,23
0,0871
1,09
1,52
0,66
0,3599
0,4345
0,2422
0,2454
0,4357
0,0910
0,3621
0,24
1,10
1,53
0,67
0,25
0,2486
0,68
0,0948
0,3643
1,11
1,54
0,4370
0,3665
0,0987
0,4382
0,2517
0,26
1,12
0,69
1,55
0,1026
0,27
0,70
0,2549
0,3686
1,13
0,4394
1,56
0,3708
0,4406
0,1064
0,2580
0,28
1,14
0,71
1,57
0,2611
1,58
0,72
0,1103
1,15
0,4418
0,29
0,3729
0,1141
0,4429
0,2642
0,3749
1,16
1,59
0,73
0,30
0,4441
0,3770
1,17
0,74
1,60
0,2673
0,1179
0,31
0,2703
0,4452
0,3790
1,61
0,32
0,75
0,1217
1,18
0,4463
1,19
0,1255
0,3810
0,2734
1,62
0,76
0,33
0,3830
0,4474
0,1293
0,77
0,34
0,2764
1,63
1,20
0,2794
0,1331
0,3849
1,64
0,4484
1,21
0,78
0,35
0,4495
0,2823
0,1368
0,79
1,22
1,65
0,3869
0,36
0,1406
0,2852
0,4505
0,3883
1,23
1,66
0,80
0,37
0,81
0,2881
0,1443
0,38
1,24
0,4515
0,3907
1,67
0,4525
0,3925
0,1480
0,2910
0,82
1,25
0,39
1,68
0,1517
0,83
0,2939
1,69
0,40
0,4535
1,26
0,3944
0,4545
0,3962
0,1554
0,2967
0,84
1,70
0,41
1,27
0,4554
1,71
1,28
0,85
0,1591
0,3980
0,2995
0,42
0,3023
0,1628
0,3997
0,4564
1,72
1,29
0,43
0,86
0,3051
0,87
1,73
1,30
0,1664
0,44
0,4573
0,4015
0,3078
0,1700
0,4032
0,4582
1,31
0,88
1,74
0,3106
0,89
0,4591
0,4049
1,32
1,75
0,4066
0,3133
0,4599
1,76
1,33
0,4608
0,4082
1,77
1,34
0,4616
0,4099
1,78
1,79
0,4625
0,4633
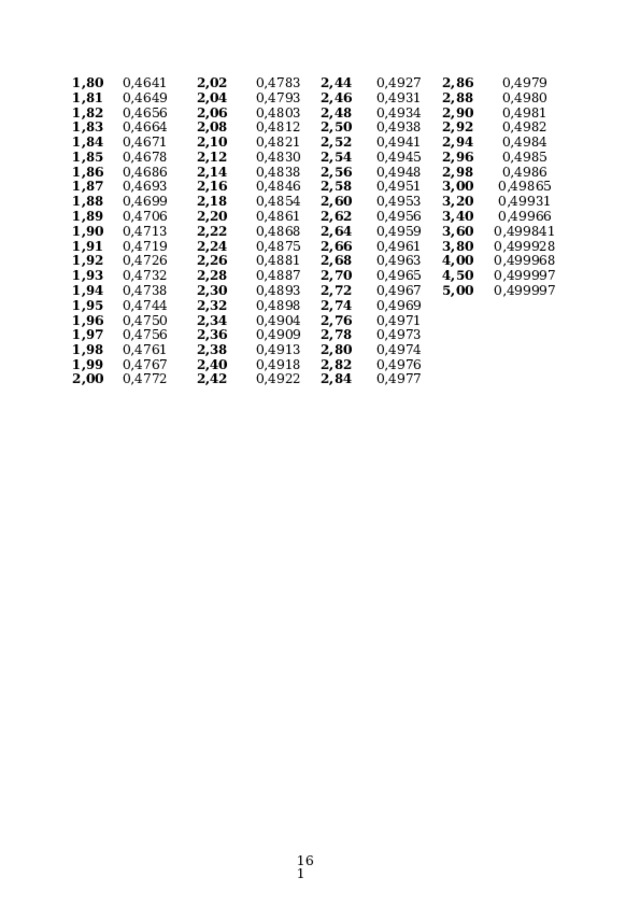
1,80
0,4641
1,81
0,4649
2,02
1,82
0,4783
2,04
0,4656
1,83
0,4793
2,44
1,84
2,06
0,4664
2,46
0,4927
0,4671
1,85
2,08
0,4803
2,86
0,4931
1,86
0,4812
2,10
2,48
0,4678
2,88
0,4979
0,4934
2,50
1,87
0,4686
0,4821
2,12
0,4980
1,88
0,4693
2,14
0,4830
2,52
2,90
0,4938
2,92
0,4941
2,54
0,4699
0,4981
1,89
0,4838
2,16
0,4706
2,18
0,4846
1,90
2,94
2,56
0,4982
0,4945
0,4713
0,4948
2,58
2,96
1,91
0,4854
2,20
0,4984
1,92
2,22
0,4861
0,4719
0,4951
2,60
2,98
0,4985
1,93
0,4953
3,00
0,4726
0,4986
0,4868
2,24
2,62
0,4732
1,94
2,26
0,4875
0,4956
2,64
3,20
0,49865
0,4738
3,40
2,28
0,49931
1,95
0,4881
2,66
0,4959
0,49966
1,96
2,68
3,60
0,4961
0,4887
2,30
0,4744
0,4750
2,32
1,97
0,4893
0,499841
3,80
2,70
0,4963
0,4756
4,00
1,98
2,34
0,499928
0,4898
2,72
0,4965
0,499968
2,36
2,74
1,99
0,4967
0,4904
0,4761
4,50
0,4767
2,38
2,00
0,499997
0,4909
2,76
5,00
0,4969
0,4971
0,4913
2,78
0,499997
2,40
0,4772
2,80
0,4918
0,4973
2,42
0,4974
2,82
0,4922
2,84
0,4976
0,4977
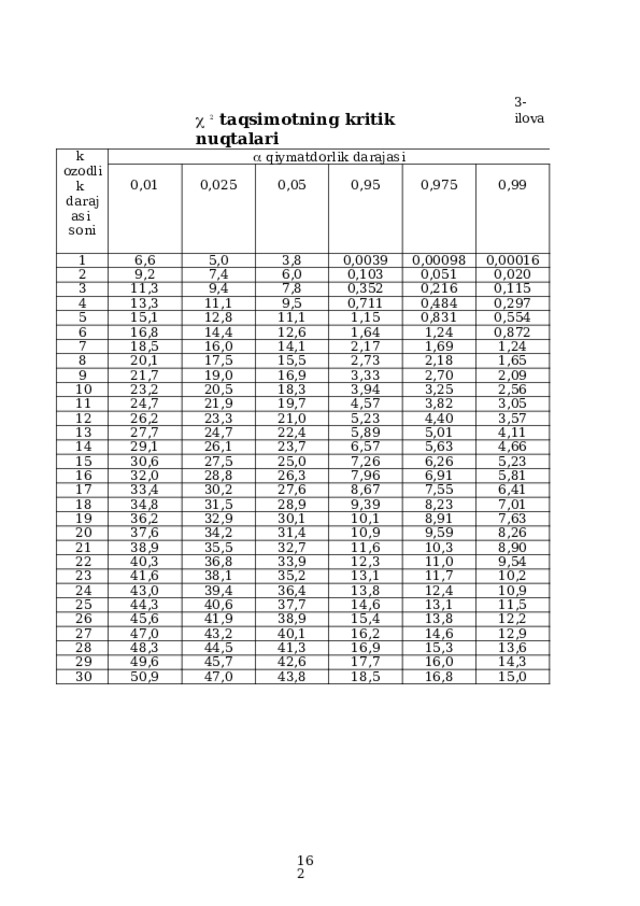
3-ilova
2 taqsimotning kritik nuqtalari
k o z odlik d a r a jasi soni
qiymatdorlik darajasi
1
0,01
6,6
2
0,025
9,2
5,0
3
3,8
11,3
0,05
4
7,4
5
0,95
0,0039
13,3
9,4
6,0
15,1
7,8
0,975
0,00098
6
11,1
0,103
12,8
0,99
7
0,051
9,5
0,00016
0,352
16,8
18,5
0,216
11,1
0,711
8
14,4
0,020
9
12,6
16,0
0,484
1,15
0,115
20,1
0,831
14,1
21,7
1,64
0,297
10
17,5
11
23,2
19,0
0,554
15,5
1,24
2,17
24,7
1,69
16,9
0,872
2,73
12
20,5
26,2
18,3
21,9
3,33
1,24
2,18
13
19,7
2,70
23,3
14
27,7
1,65
3,94
4,57
3,25
21,0
29,1
2,09
24,7
15
3,82
30,6
26,1
16
22,4
5,23
2,56
32,0
23,7
3,05
4,40
5,89
27,5
17
3,57
18
33,4
5,01
25,0
28,8
6,57
34,8
26,3
5,63
19
7,26
30,2
4,11
36,2
31,5
7,96
4,66
27,6
6,26
20
6,91
28,9
37,6
5,23
32,9
8,67
21
34,2
30,1
22
38,9
9,39
7,55
5,81
31,4
40,3
8,23
35,5
10,1
23
6,41
24
36,8
32,7
8,91
7,01
10,9
41,6
9,59
33,9
43,0
11,6
25
7,63
38,1
44,3
39,4
26
35,2
12,3
10,3
8,26
11,0
36,4
45,6
27
40,6
8,90
13,1
28
47,0
41,9
9,54
37,7
13,8
11,7
48,3
12,4
38,9
29
43,2
14,6
10,2
13,1
40,1
30
49,6
15,4
10,9
44,5
50,9
41,3
13,8
45,7
11,5
16,2
16,9
14,6
42,6
12,2
47,0
15,3
43,8
12,9
17,7
13,6
16,0
18,5
16,8
14,3
15,0
Foydalanilgan adabiyotlar
- Аbdushukurov А.А. Xi-kvadrat kriteriysi: nazariyasi va tatbiqi, O‗zMU, 2006.
- Аbdushukurov А.А. , Azlarov T . A ., Djamirzayev A . A . Ehtimollar
nazariyasi va matematik statistikadan misol va masalalar to‗plami. Toshkent «Universitet», 2003.
- Azlarov T .A., Abdushukurov A.A. Ehtimollar nazariyasi va matematik
statistikadan Inglizcha-ruscha-o‗zbekcha lug‗at. Toshkent: «Universitet», 2005.
- Abdushukurov A. A. Ehtimollar nazariyasi. Ma‘ruzalar matni. Toshkent:
«Universitet», 2000.
- Бочаров П. П., Печинкин А. В. Теория вероятностей. Математическая статистика. - 2-е изд. - М.: ФИЗМАТЛИТ, 2005.
- Ватутин В.А., Ивченко Г.И., Медведев Ю.И., Чистяков В.П.
Теория вероятностей и математическая статистика в задачах М.: 2003.
- Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: Высшая школа, 1984.
- Кибзун А. И., Горяинова Е. Р., Наумов А. В., Сиротин А. Н. Теория
вероятностей и математическая статистика. Базовый курс с примерами и задачами / Учебн. пособие. - М.: ФИЗМАТЛИТ, 2002.
- Кибзун А.И., Панков А.Р., Сиротин А.Н. Учебное пособие по
теории вероятностей. — М.: Изд-во МАИ, 1993.
- Коршунов Д.А., Чернова Н.И. Сборник задач по математической статистике: учебное пособие. 2-е изд., испр. –Новосибирск, изд-во Института математики, 2004.
- Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. 2-е изд., перераб. и доп.- М.: ЮНИТИДАНА, 2004.
- Максимов Ю.Д. Куклин Б.А., Хватов Ю.А. Математика. Выпуск 6. Теория вepoятностей. Контрольные задания с образцами решений.
Тесты. Конспект-справ. / Под ред. Ю.Д. Максимова СПб.: Изд-во ИЗkВО СПбГТУ, 2002.
- Максимов Ю.Д. Маreматика. Выпуск 8. Матeматическая
статистика: Опорный конспект. СПб.: Изд-во ИЗkВО СПбГТУ, 2002.
- Писм е нн ый Д.Т. К о нспе кт л е кц и й п о те о р и и в ер о я тно с тей и математической статистике. М.: Айрис-пресс, 2004.

- Пугачев B.C. Теория вероятностей и математическая статистика. М.: Учеб. пособие. 2-е изд., исправл. и допол. М.: ФИЗМАТЛИТ, 2002.
- http://www.el.tfi.uz/pdf/enmcoq22.uzl.pdf ; 17. http://www.nsu.ru/icem/grants/etfm/ ; 18. http://www.lib.homelinex.org/math/ ; 19. http://www.eknigu.com/lib/mathematics/ ; 20. http://www.eknigu.com/info/M_Mathematics/MC .














