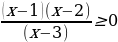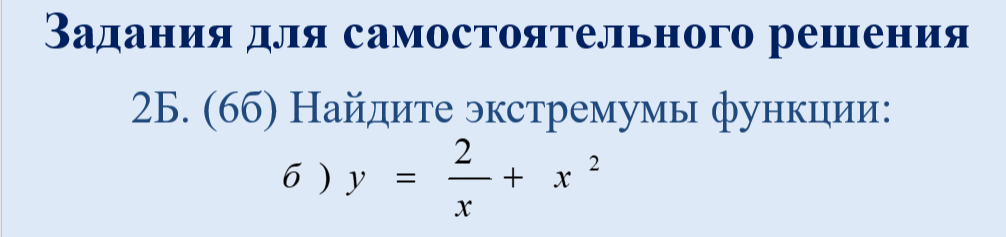Экстремумы функции

Учитель Кузьмин В. А. дата: 29.11.2023

Тема: «Экстремумы функции»

Цели урока:

Образовательные:

1. Опираясь на знания учащихся по производной функции помочь сформулировать и осознать определение понятий критических, стационарных точек и точек экстремума; подвести к гипотезе: необходимое и достаточное условие существования экстремума функции.

2. Создать условие для первичного закрепления учащимися умения аналитически и графически определять наличие у функции критических, стационарных точек и точек экстремума.

3. Подготовить учащихся к сдаче ЕГЭ.

Развивающие:

Способствовать развитию учебно-познавательной деятельности, логического мышления.

Воспитательные:

1. Сформировать умения наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии.

2. Развивать мышление, внимание, речь учащегося.

3. Сформировать обще трудовые умения в условиях наибольшей ответственности и ограниченности во времени.

4. Воспитывать умение прислушиваться к другому мнению и отстаивать свою точку зрения.

Тип урока: урок ознакомления с новым материалом.

Ход урока:

I. Организационный момент (Метод информационно-сообщающий)

1. Актуализация знаний. «Мозговой штурм»

1.Вычислить производную функции: ( задание выполняется самостоятельно, с дальнейшей самопроверкой, количество правильных заданий отмечают в листе самоконтроля)

2. Решить неравенство: ( у доски)

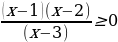
А) f(x) = 3х – 9 ( 1 балл)

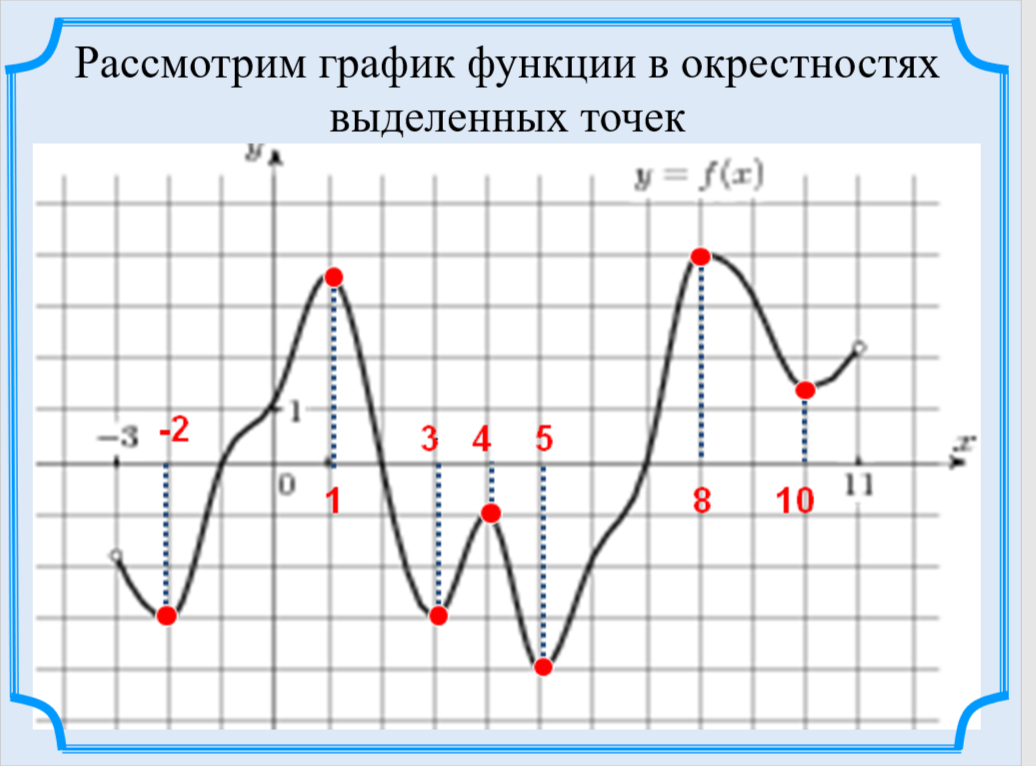
Определения

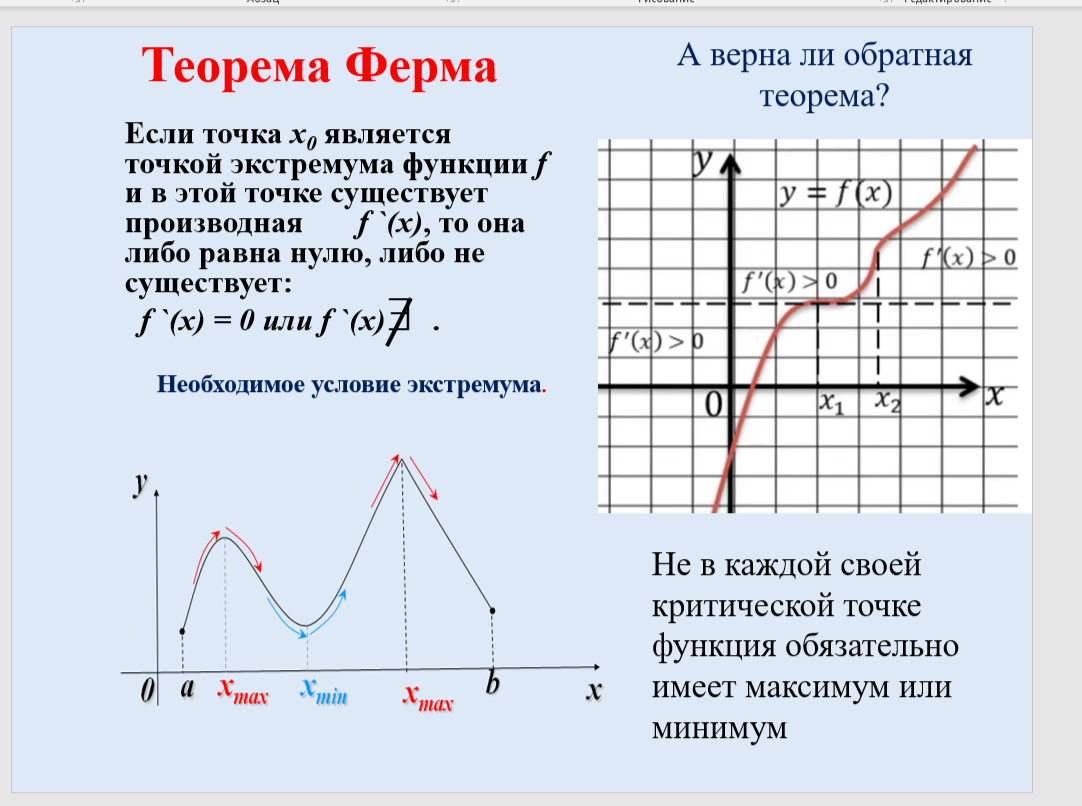
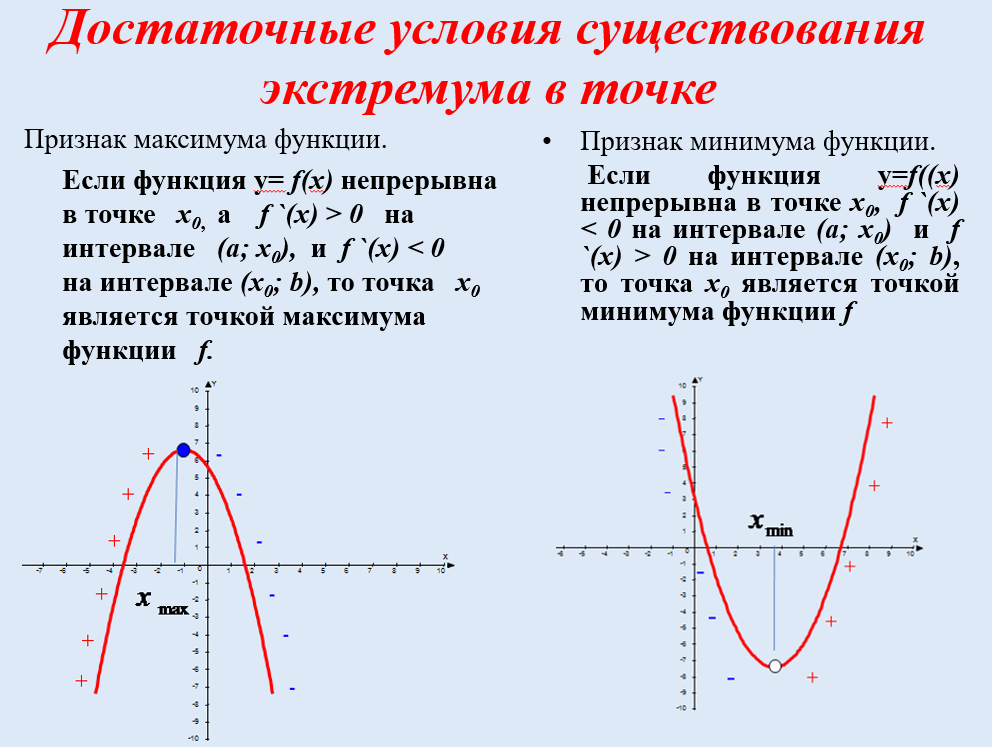
Работа с материалами ЕГЭ

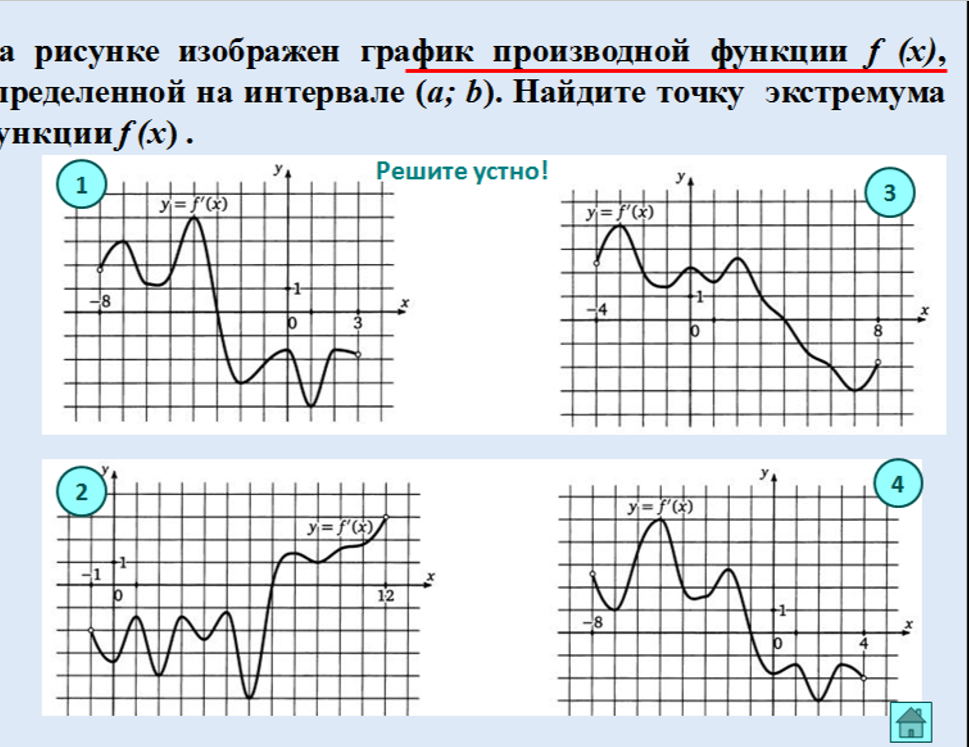
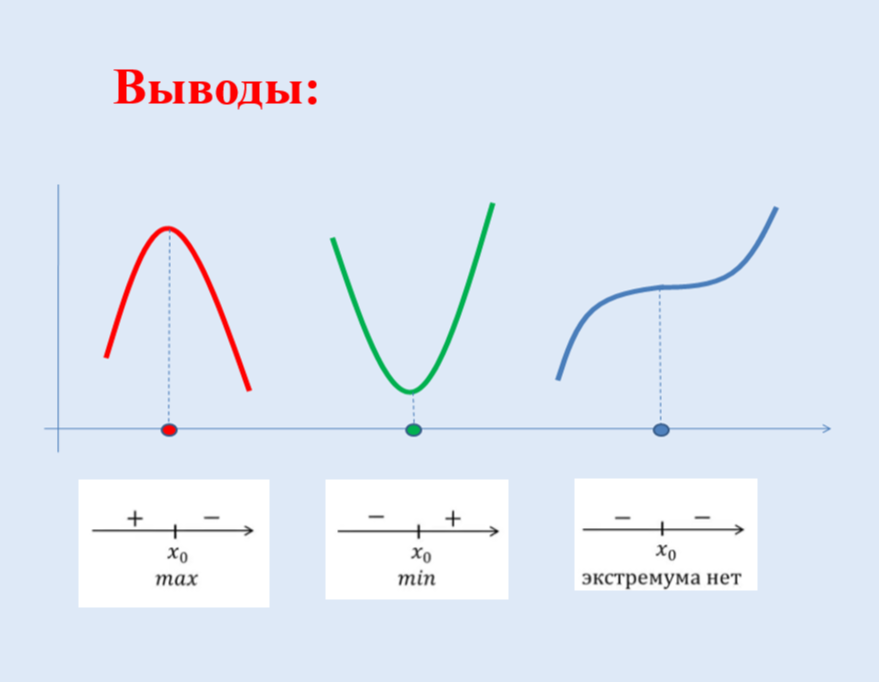
Составить алгоритм нахождения точек экстремума функции.

1. Найти область определения функции.

2. Найти f'(x).

3. Найти критические  точки, т.е. точки, где  f'(x) = 0 или f'(x) не существует.
(Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Расположить область определения и эти точки на координатной прямой.

5. Определить знаки производной на    каждом из интервалов

6. Применить признаки.

7. Записать ответ.

(Практический метод) (

Самостоятельно решаем у доски

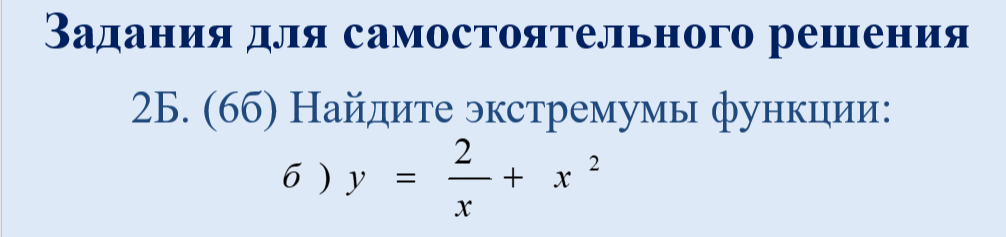
Резерв

Рефлексия : что понравилось? что нет?