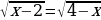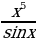Государственное автономное профессиональное образовательное учреждение
Мурманской области
«МУРМАНСКИЙ СТРОИТЕЛЬНЫЙ КОЛЛЕДЖ ИМ. Н.Е. МОМОТА»
Экзаменационные задания по учебной дисциплине
«Математика: алгебра и начала математического анализа; геометрия»
для специальностей ППСЗ
Мурманск
2025 г.
Организация-разработчик:
Государственное автономное профессиональное образовательное учреждение Мурманской области «МУРМАНСКИЙ СТРОИТЕЛЬНЫЙ КОЛЛЕДЖ ИМ. Н.Е. МОМОТА»
Разработчик:
Новикова Е.В., преподаватель Мурманского строительного колледжа
| Рассмотрена и одобрена предметно-цикловой комиссией «Естественнонаучные дисциплины» Председатель _______ И.А.Егорова Протокол № _____ от «___» _______________ 2025г. |
Содержание
| Пояснительная записка | 4 |
| Вариант 1 | 5-6 |
| Вариант 2 | 7-8 |
| Вариант 3. | 9-10 |
| Вариант 4 | 11-12 |
| Вариант 5 | 13-14 |
| Вариант 6 | 15-16 |
| Вариант 7 |
|
| Вариант 8 |
|
| Вариант 9 |
|
| Вариант 10 |
|
Пояснительная записка
Экзаменационные задания по учебной дисциплине «Математика: алгебра и начала математического анализа; геометрия» для специальностей ППСЗ составлены в соответствии с образовательной программой среднего общего образования в пределах освоения основной профессиональной образовательной программы СПО на базе основного общего образования.
Задания подразделяются на 3 уровня. В первой группе составлены задания базового уровня знаний на оценку «3». Задания из первой группы оцениваются в 1 балл.
Задания из второй группы оцениваются в 2 балла. Задания имеют повышенный уровень и за правильно выполненные задания из 1 и 2 уровня ставится оценка «4».
Задания из третьей группы оцениваются в 3 балла. Задания составлены для проверки углубленного знания математики. Максимальное возможное количество баллов – 23.
На оценку «3» необходимо набрать 10 баллов.
На оценку «4» необходимо набрать 20 баллов.
На оценку «5» необходимо набрать 23 балла.
Экзаменационная работа
Вариант 1
Уровень 1
Найдите значение выражения:  8·(0,2+1,6) -2,7
8·(0,2+1,6) -2,7
На бензоколонке один литр бензина стоит 43 рубля 60 копеек. Водитель залил в бак 15 литров бензина и купил бутылку воды за 68 рублей. Сколько сдачи он должен получить с 1000 рублей?
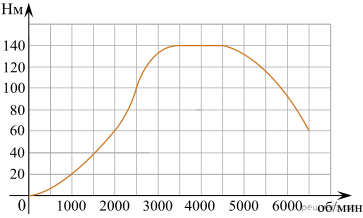
На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в Н · м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 60 Н · м. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения 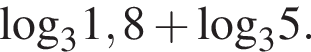
Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
| Перевозчик | Стоимость перевозки одним автомобилем (руб. на 100 км) | Грузоподъемность автомобилей (тонн) |
| А | 3200 | 3,5 |
| Б | 4100 | 5 |
| В | 9500 | 12 |
Решите уравнение: 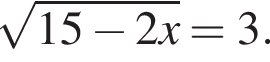
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
Работа постоянного тока (в джоулях) вычисляется по формуле 𝐴= 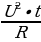 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 3 c, U = 10 В и R = 12 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 3 c, U = 10 В и R = 12 Ом.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 2 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑠𝑖𝑛2𝛼, если 𝑐𝑜𝑠𝑥=0,6 и 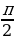 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 2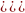 +5
+5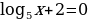
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Найдите производную функции: 𝑓(𝑥)= 2𝑥5+ 3𝑐𝑜𝑠𝑥−5
Решите неравенство: sin2x≥0
Уровень 3
Вычислите площадь фигуры, ограниченную линиями: y=x2, y=0, x=4
Экзаменационная работа
Вариант 2
Уровень 1
Найдите значение выражения: 2,4+1,56:1,3-5,4
Для приготовления яблочного варенья на 1 кг яблок нужно 1,2 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 14 кг яблок?
На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в Н · м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 60 Н · м. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?

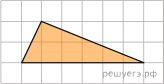
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите значение выражения: 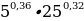
Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
| Тарифный план | Абонентская плата | Плата за трафик |
| План «0» | Нет | 2,5 руб. за 1 Мб |
| План «500» | 550 руб. за 500 Мб трафика в месяц | 2 руб. за 1 Мб сверх 500 Мб |
| План «800» | 700 руб. за 800 Мб трафика в месяц | 1,5 руб. за 1 Мб сверх 800 Мб |
Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб?
Решите уравнение: 
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество целых точек, в которых график функции возрастает.
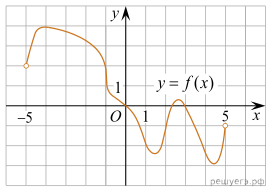
Площадь треугольника можно вычислить по формуле 𝑆=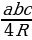 где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 10, S = 36 и R =
где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 10, S = 36 и R =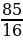 .
.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 80 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
2 уровень
Найдите 𝑐𝑜𝑠2𝛼, если 𝑠𝑖𝑛𝑥=0,6 и 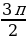 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 0,25x+1,5·0,5x -1=0
Площадь боковой поверхности цилиндра равна 96π, а диаметр его основания – 12. Найдите высоту цилиндра.
Найдите производную функции: f(x)=x3·tgx
Решите неравенство: 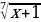 ≥-2
≥-2
3 уровень
Напишите уравнение касательной к графику функции y=x2+3x в точке xo=1.
Экзаменационная работа
Вариант 3
Уровень 1
Найдите значение выражения: (48,96-37,29) ·1,3-3,6
Стоимость проезда в маршрутном такси составляет 20 рублей. Какое наибольшее число поездок можно будет совершить в этом маршрутном такси на 150 рублей, если цена проезда снизится на 10%?
На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
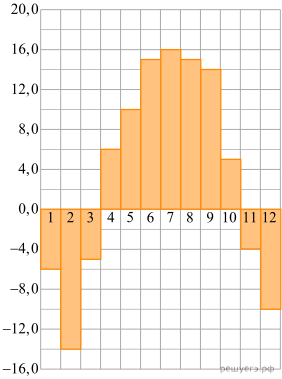
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения 36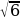 ·tg
·tg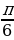 ·sin
·sin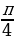
Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
| Тарифный план | Абонентская плата | Плата за трафик |
| План «0» | Нет | 2,5 руб. за 1 Мб |
| План «500» | 550 руб. за 500 Мб трафика в месяц | 2 руб. за 1 Мб сверх 500 Мб |
| План «800» | 700 руб. за 800 Мб трафика в месяц | 1,5 руб. за 1 Мб сверх 800 Мб |
Пользователь предполагает, что его трафик составит 600 Мб в месяц и, исходя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 600 Мб?
Решите уравнение: 24-2х=64
Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=3x3+2x-5 в точке xo=2.
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле 𝑔=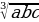 . Вычислите среднее геометрическое чисел 5, 25 и 27.
. Вычислите среднее геометрическое чисел 5, 25 и 27.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑡𝑔𝛼, если 𝑐𝑜𝑠𝑥=0,6 и 0𝛼 .
Решите уравнение: 6cos2x+cosx-1=0
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Найдите производную функции: f(x)=sin(2x3+5)
Решите неравенство: 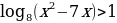
Уровень 3
Вычислите площадь фигуры, ограниченную линиями: y=x3, y=0, x=-3, x=1.
Экзаменационная работа
Вариант 4
Уровень 1
Найдите значение выражения: 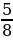 ÷ (2
÷ (2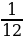 - 4
- 4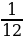 ·
·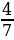 )
)
Для приготовления вишневого варенья на 1 кг вишни нужно 1,3 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 40 кг вишни?
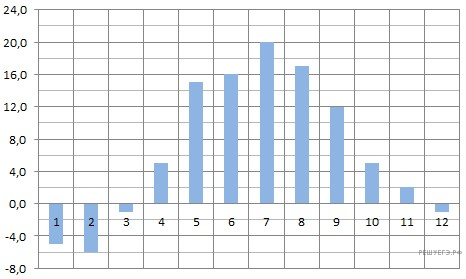
На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения 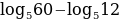
Для остекления музейных витрин требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 м2. В таблице приведены цены на стекло и на резку стекол. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена стекла (руб. за 1 м2) | Резка стекла (руб. за одно стекло) | Дополнительные условия |
| A | 300 | 17 | |
| Б | 320 | 13 | |
| В | 340 | 8 | При заказе на сумму больше 2500 руб. резка бесплатно. |
Решите уравнение: sin 2x=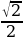
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
Работа постоянного тока (в джоулях) вычисляется по формуле 𝐴=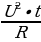 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 18 c, U = 7 В и R = 14 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 18 c, U = 7 В и R = 14 Ом.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите c𝑡𝑔𝛼, если 𝑐𝑜𝑠𝑥=0,6 и 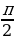 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 3·9x-10·3x+3=0
Объем цилиндра равен 216π, а его высота – 6. Найдите радиус основания цилиндра.
Найдите производную функции: f(x)=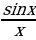
Решите неравенство: 45x-1≤163x+2
Уровень 3
Напишите уравнение касательной к графику функции y=x3-2x в точке xo=-1.
Экзаменационная работа
Вариант 5
Уровень 1
Найдите значение выражения: 9-3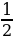 ·(1
·(1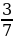 +2
+2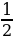 )
)
Для приготовления маринада для огурцов на 1 литр воды требуется 8 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 13 литров маринада?
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января. Ответ дайте в градусах Цельсия.
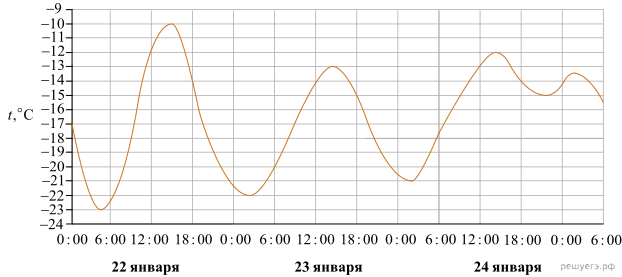
Ответ дайте в градусах Цельсия.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения 48·1110:448
От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.
| | 1 | 2 | 3 |
| Автобусом | От дома до автобусной станции — 15 мин | Автобус в пути: 2 ч 15 мин. | От остановки автобуса до дачи пешком 5 мин. |
| Электричкой | От дома до станции железной дороги — 25 мин. | Электричка в пути: 1 ч 45 мин. | От станции до дачи пешком 20 мин. |
| Маршрутным такси | От дома до остановки маршрутного такси — 25 мин. | Маршрутное такси в дороге: 1 ч 35 мин. | От остановки маршрутного такси до дачи пешком 40 минут |
Решите уравнение: 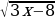 =5
=5
На рисунке изображен график y=f '(x) — производной функции y=f(x) определенной на интервале (-6;6). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
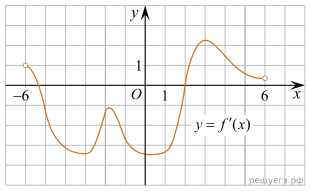
Площадь треугольника можно вычислить по формуле 𝑆=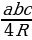 где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 5, S = 18 и R =
где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 5, S = 18 и R = 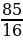 .
.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 60 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑠𝑖𝑛2𝛼, если 𝑐𝑜𝑠𝑥=0,8 и 𝜋 𝛼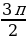 .
.
Решите уравнение: 2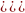 -4
-4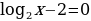
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3.
Найдите производную функции: f(x)=52x+3
Решите неравенство: cos 3x ≤-1
Уровень 3
Вычислите площадь фигуры, ограниченную линиями: y=x2, y=0, x=-3.
Экзаменационная работа
Вариант 6
Уровень 1
Найдите значение выражения (2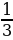 :2
:2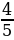 -1)·2
-1)·2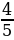
Таксист за месяц проехал 9000 км. Цена бензина 30 рублей за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?
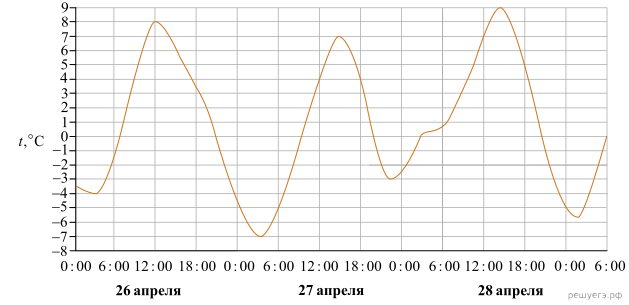
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 27 апреля. Ответ дайте в градусах Цельсия.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения: -4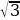 cos(-750o)
cos(-750o)
Клиент хочет арендовать автомобиль на сутки для поездки протяженностью 500 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?
| Автомобиль | Топливо | Расход топлива (л на 100 км) | Арендная плата (руб. за 1 сутки) |
| А | Дизельное | 7 | 3700 |
| Б | Бензин | 10 | 3200 |
| В | Газ | 14 | 3200 |
Цена дизельного топлива — 19 рублей за литр, бензина — 22 рублей за литр, газа — 14 рублей за литр.
Решите уравнение: 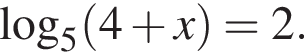
Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=x-ln x в его точке с абсциссой x=3.
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле 𝑔=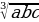 . Вычислите среднее геометрическое чисел 6, 36 и 27.
. Вычислите среднее геометрическое чисел 6, 36 и 27.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 90 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑐𝑜𝑠2𝛼, если 𝑠𝑖𝑛𝑥=0,8 и 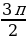 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 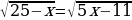
Высота прямого кругового конуса равна 3 см, образующая – 5 см. Найдите его объем.
Найдите производную функции: f(x)=cosx·ctgx
Решите неравенство: 11-7х+1˃121-2х-10
Уровень 3
Найдите промежутки монотонности и экстремумы функции: f(x)=3x2-x3
Экзаменационная работа
Вариант 7
Уровень 1
Найдите значение выражения: 2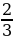 ·1
·1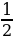 -1,5:
-1,5: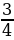
В доме, в котором живет Петя, один подъезд. На каждом этаже находится по 6 квартир. Петя живет в квартире № 50. На каком этаже живет Петя?
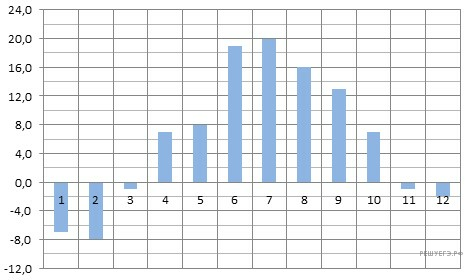
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
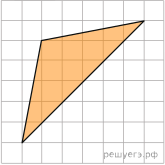
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите значение выражения: (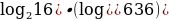
Телефонная компания предоставляет на выбор три тарифных плана.
| Тарифный план | Абонентская плата | Плата за 1 минуту разговора |
| Повременный | 135 руб. в месяц | 0,3 руб. |
| Комбинированный | 255 руб. за 450 мин. в месяц | 0,28 руб. за 1 мин. сверх 450 мин. в месяц |
| Безлимитный | 380 руб. в месяц | |
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 650 минут? Ответ дайте в рублях.
Решите уравнение: 5x-7=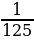
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени с.
Работа постоянного тока (в джоулях) вычисляется по формуле 𝐴=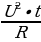 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 15 c, U = 6 В и R = 9 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 15 c, U = 6 В и R = 9 Ом.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 60 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑡𝑔𝛼, если 𝑐𝑜𝑠𝑥=0,8 и 0𝛼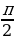 .
.
Решите уравнение: 3sin2x-5sinx-2=0
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды.
Найти производную функции: f(x)=6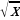 +13x10
+13x10
Решите неравенство: 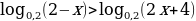
Уровень 3
Вычислите площадь фигуры, ограниченную линиями: y=x4, y=0, x=-1, x=2.
Экзаменационная работа
Вариант 8
Уровень 1
Найдите значение выражения:0,4+0,2·(1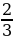 -4
-4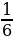 )
)
В обменном пункте 1 тенге стоит 4 рубля 50 копеек. Отдыхающие обменяли рубли на тенге и купили 5 кг огурцов по цене 6 тенге за 1 кг. Во сколько рублей обошлась им эта покупка?
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
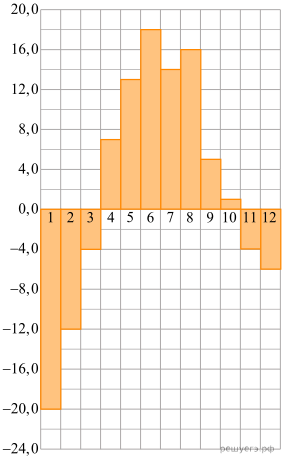
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите значение выражения: (512)3:537
Строительный подрядчик планирует купить 5 тонн облицовочного кирпича у одного из трех поставщиков. Вес одного кирпича 5 кг. Цены и условия доставки приведены в таблице. Во сколько рублей обойдется наиболее дешевый вариант покупки?
| Поставщик | Цена кирпича (руб. за шт) | Стоимость доставки (руб.) | Специальные условия |
| А | 17 | 7000 | Нет |
| Б | 18 | 6000 | Если стоимость заказа выше 50 000 руб., доставка бесплатно |
| В | 19 | 5000 | При заказе свыше 60 000 руб. доставка со скидкой 50%. |
Решите уравнение: cos 3x=-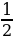
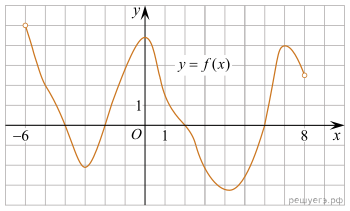
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Площадь треугольника можно вычислить по формуле 𝑆=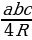 где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите a, если b = 18, с = 10, S = 72 и R =
где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите a, если b = 18, с = 10, S = 72 и R =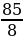 .
.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑐𝑡𝑔𝛼, если 𝑐𝑜𝑠𝑥=0,8 и 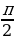 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 2·4x-5·2x+2=0
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
Найти производную функции: f(x)=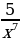 - ex
- ex
Решите неравенство: 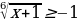
Уровень 3
Найдите промежутки монотонности и экстремумы функции: f(x)=6x+x3
Экзаменационная работа
Вариант 9
Уровень 1
Найдите значение выражения:  ·
·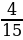 -
- 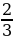 ):(-8)
):(-8)
Для покраски 1 кв.м. потолка требуется 200 г краски. Краска продается в банках по 2 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 64 кв.м.?
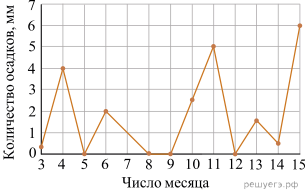
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало  миллиметров осадков.
миллиметров осадков.
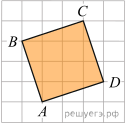
Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите значение выражения: 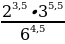
Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
| Поставщик | Цена бруса(руб. за 1 м3) | Стоимость доставки | Дополнительные условия |
| A | 4200 | 10200 | |
| Б | 4800 | 8200 | При заказе на сумму больше 150 000 руб. доставка бесплатно |
| В | 4300 | 8200 | При заказе на сумму больше 200 000 руб. доставка бесплатно |
Решите уравнение: 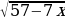 =6
=6
Найдите угловой коэффициент касательной, проведенной к графику функции f(x)=3x3+2x-5 в его точке с абсциссой x=2.
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле 𝑔=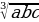 . Вычислите среднее геометрическое чисел 9, 12 и 16.
. Вычислите среднее геометрическое чисел 9, 12 и 16.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑠𝑖𝑛2𝛼, если 𝑐𝑜𝑠𝑥=0,6 и 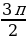 𝛼𝜋.
𝛼𝜋.
Решите уравнение: 2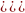 -4
-4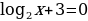
Объём конуса равен 64π, а его высота равна 12. Найдите радиус основания конуса.
Найти производную функции: f(x)=(cosx)2x+3
Решите неравенство: (0,1)-3х-0,5≤(0,1)х+1,5
Уровень 3
Вычислите площадь фигуры, ограниченную линиями: y=x3+2, y=0, x=0, x=2.
Экзаменационная работа
Вариант 10
Уровень 1
Найдите значение выражения 4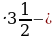 )
)
Ананасы стоят 85 рублей за штуку. Какое максимальное число ананасов можно купить на 500 рублей, если их цена снизится на 20%?
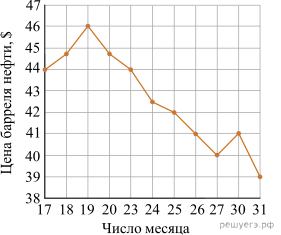
На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 17 по 31 августа 2004 года. По горизонтали указываются числа месяца, по вертикали — цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену нефти на момент закрытия торгов в указанный период (в долларах США за баррель).
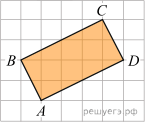
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите значение выражения: 24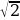 cos
cos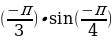
В таблице даны условия банковского вклада в трех различных банках. Предполагается, что клиент кладет на счет 10 000 рублей на срок 1 год. В каком банке к концу года вклад окажется наибольшим? В ответе укажите сумму этого вклада в рублях.
| Банк | Обслуживание счета * | Процентная ставка (% годовых) ** |
| Банк А | 40 руб. в год | 2 |
| Банк Б | 8 руб. в месяц | 3,5 |
| Банк В | Бесплатно | 1,5 |
* В начале года или месяца со счета снимается указанная сумма в уплату за ведение счета
** В конце года вклад увеличивается на указанное количество процентов.
Решите уравнение: 16x-9=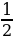
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Работа постоянного тока (в джоулях) вычисляется по формуле 𝐴=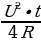 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 8 c, U = 6 В и R = 2 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 8 c, U = 6 В и R = 2 Ом.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 10 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 30 см. Ответ дайте в кубических сантиметрах.
Уровень 2
Найдите 𝑐𝑜𝑠2𝛼, если 𝑠𝑖𝑛𝑥=0,6 и π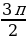 .
.
Решите уравнение: 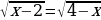
В основании прямой призмы лежит прямоугольный треугольник, катеты которого равны 11 и 5. Найдите объём призмы, если её высота равна 4.
Найти производную функции: f(x)=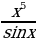
Решите неравенство: lg(8x-16)˂lg(3x+1)
Уровень 3
Найдите промежутки монотонности и экстремумы функции: f(x)=x3+3x2
33






 8·(0,2+1,6) -2,7
8·(0,2+1,6) -2,7

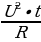 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 3 c, U = 10 В и R = 12 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 3 c, U = 10 В и R = 12 Ом. 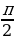 𝛼𝜋.
𝛼𝜋. 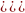 +5
+5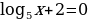

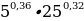
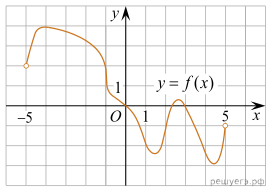
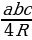 где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 10, S = 36 и R =
где a, b и c – стороны треугольника, а R – радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если a = 9, с = 10, S = 36 и R =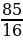 .
.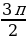 𝛼𝜋.
𝛼𝜋.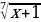 ≥-2
≥-2

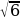 ·tg
·tg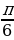 ·sin
·sin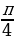
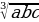 . Вычислите среднее геометрическое чисел 5, 25 и 27.
. Вычислите среднее геометрическое чисел 5, 25 и 27. 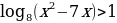
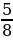 ÷ (2
÷ (2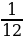 - 4
- 4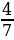 )
)

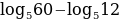
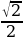
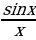
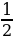 ·(1
·(1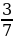 +2
+2

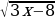 =5
=5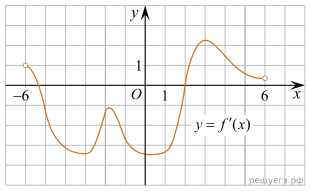
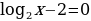
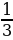 :2
:2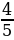 -1)·2
-1)·2

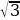 cos(-750o)
cos(-750o)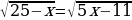
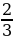 ·1
·1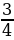


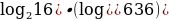
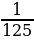
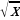 +13x10
+13x10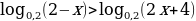
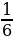 )
)


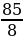 .
. 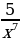 - ex
- ex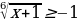
 ·
·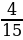 -
- 

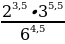
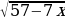 =6
=6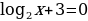
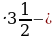 )
)

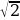 cos
cos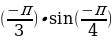
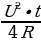 , где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 8 c, U = 6 В и R = 2 Ом.
, где U – напряжение (в вольтах), R – сопротивление (в омах), t – время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 8 c, U = 6 В и R = 2 Ом.