Экзаменационный материал для проведения промежуточной аттестации по математике (углубленный уровень) в 10 классе
Пояснительная записка к экзаменационным билетам
для промежуточной аттестации
Билеты для промежуточной аттестации по математике в письменной форме за курс 10 класса составлены в соответствии с требованиями федерального государственного образовательного стандарта среднего общего образования (приказ Министерства образования и науки РФ от 17 мая 2012 г. N 413).
Экзаменационные материалы разработаны с учетом требований федеральной рабочей программы учебных предметов «Алгебра и начала математического анализа. Углубленный уровень», «Вероятность и статистика. Углубленный уровень» и «Геометрия. Углубленный уровень».
Экзаменационный материал составлен в формате ГИА в связи с подготовкой к ЕГЭ в следующем учебном году.
Содержание разработано по основным темам курса математики:
Стереометрия
Начала теории вероятностей и вероятность сложных событий
Логарифмические уравнения
Тригонометрические выражения и преобразования
Задачи с прикладным содержанием
Текстовые задачи на движение
Графики функций
Тригонометрические уравнения
Логарифмические неравенства
Финансовые задачи.
К комплекту билетов имеется приложение с решением 2-ой части, а также критерии оценивания ответов.
Спецификация к экзаменационным билетам
для промежуточной аттестации по математике (профильный уровень)
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей и включает в себя 15 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 12 заданий (задания 1–12) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 3 задания (задания 13–15) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне.
Задание с кратким ответом (1–12) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
При выполнении заданий с развернутым ответом части 2 экзаменационной работы в бланке ответов № 2 должны быть записаны полное обоснованное решение и ответ для каждой задачи.
В таблице 1 приведено распределение заданий по частям экзаменационной работы.
Таблица 1
Распределение заданий по частям экзаменационной работы
| Часть работы | Количество заданий | Максимальный первичный балл | Процент максимального первичного балла за выполнение заданий данной части от максимального первичного балла за всю работу, равного 18 | Тип заданий |
| Часть 1 | 12 | 12 | 67 | С кратким ответом |
| Часть 2 | 3 | 6 | 33 | С развернутым ответом |
| Итого | 15 | 18 | 100 |
|
Распределение заданий экзаменационного варианта по содержанию, видам умений и способам действий.
Задания части 1 проверяют следующий учебный материал.
1. Алгебра и начала математического анализа, 10 класс.
2. Вероятность и статистика, 10 класс.
3. Геометрия, 10 класс.
Задания части 2 проверяют следующий учебный материал.
1. Алгебра и начала математического анализа, 10 класс.
2. Геометрия, 10 класс.
В таблице 2 приведено распределение заданий экзаменационной работы по содержательным разделам курса математики.
Таблица 2
Распределение заданий экзаменационной работы
по содержательным разделам курса математики
| Содержательные разделы | Количество заданий | Максимальный первичный балл | Процент максимального первичного балла за выполнение заданий данной части от максимального первичного балла за всю работу, равного 18 |
| Алгебра и начала математического анализа | 10 | 13 | 72,2 |
| Геометрия | 3 | 3 | 16,7 |
| Вероятность и статистика | 2 | 2 | 11,1 |
| Итого: | 15 | 18 | 100 |
Содержание экзаменационной работы даёт возможность проверить комплекс умений по предмету:
уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни;
уметь выполнять вычисления и преобразования;
уметь решать уравнения и неравенства;
уметь выполнять действия с функциями;
уметь выполнять действия с геометрическими фигурами, координатами и векторами;
уметь строить и исследовать математические модели.
Распределение заданий экзаменационного варианта по уровням сложности.
Часть 1 содержит 7 заданий базового уровня (задания 1-4, 6-8) и 5 заданий повышенного уровня (задания 5, 9-12). Часть 2 содержит 3 задания повышенного уровня (задания 13-15).
В таблице 4 приведено распределение заданий экзаменационной работы по уровням сложности.
Таблица 4
Распределение заданий по уровням сложности
| Уровень сложности заданий | Количество заданий | Максимальный первичный балл | Процент максимального первичного балла за выполнение заданий данной части от максимального первичного балла за всю работу, равного 15 |
| Базовый | 7 | 7 | 38,9 |
| Повышенный | 8 | 11 | 61,1 |
| Итого: | 15 | 18 | 100 |
Продолжительность экзамена
На выполнение экзаменационной работы отводится 2 часа 30 минут (150 минут).
Обобщенный план экзаменационного варианта по математике
Используются следующие условные обозначения.
Уровни сложности заданий: Б – базовый, П – повышенный, В – высокий.
| Номер задания | Проверяемые требования к предметным результатам освоения основной образовательной программы | Коды проверяемых требований (по кодификатору) | Коды проверяемых элементов содержания (по кодификатору) | Уровень сложности задания | Максимальный балл за выполнение задания | Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) |
| 1 | Умение оперировать понятиями: плоский угол, площадь фигуры, подобные фигуры; умение использовать при решении задач изученные факты и теоремы планиметрии; умение вычислять геометрические величины (длина, угол, площадь), используя изученные формулы и методы. | 9,10,11 | 7 | Б | 1 | 3 |
| 2 | Умение оперировать понятиями: вектор, координаты вектора, сумма векторов, произведение вектора на число, скалярное произведение, угол между векторами | 12 | 7 | Б | 1 | 3 |
| 3 | Умение оперировать понятиями: точка, прямая, плоскость, величина угла, плоский угол, двугранный угол, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями, объем фигуры, площадь поверхности; умение использовать геометрические отношения при решении задач; умение вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы; умение использовать при решении задач изученные факты и теоремы планиметрии | 9,10,11 | 7 | Б | 1 | 3 |
| 4 | Умение оперировать понятиями: случайное событие, вероятность случайного события; умение вычислять вероятность | 8 | 6 | Б | 1 | 2 |
| 5 | Умение оперировать понятиями: случайное событие, вероятность случайного события; умение вычислять вероятность с использованием графических методов; применять формулы сложения и умножения вероятностей, формулу полной вероятности, комбинаторные факты и формулы | 8 | 6 | П | 1 | 7 |
| 6 | Умение решать уравнения, неравенства и системы с помощью различных приемов | 3 | 2 | Б | 1 | 2 |
| 7 | Умение выполнять вычисление значений и преобразования выражений со степенями и логарифмами, преобразования дробно-рациональных выражений | 2 | 1 | Б | 1 | 3 |
| 8 | Умение оперировать понятиями: функция, экстремум функции, наибольшее и наименьшее значения функции на промежутке, производная функции, первообразная; находить уравнение касательной к графику функции; умение находить производные элементарных функций; умение использовать производную для исследования функций, находить наибольшие и наименьшие значения функций; находить площади фигур с помощью интеграла | 4 | 3,4 | Б | 1 | 5 |
| 9 | Умение моделировать реальные ситуации на языке математики; составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать построенные модели с использованием аппарата алгебры, исследовать полученное решение и оценивать правдоподобность результатов | 6 | 22 | П | 1 | 5 |
| 10 | Умение решать текстовые задачи разных типов, составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать полученное решение и оценивать правдоподобность результатов | 6 | 2 | П | 1 | 6 |
| 11 | Умение выражать формулами зависимости между величинами; использовать свойства и графики функций для решения уравнений | 5 | 3 | П | 1 | 8 |
| 12 | Умение оперировать понятиями: экстремум функции, наибольшее и наименьшее значения функции на промежутке; умение находить производные элементарных функций; умение использовать производную для исследования функций, находить наибольшие и наименьшие значения функций | 4 | 4 | П | 1 | 8 |
| 13 | Умение решать уравнения, неравенства и системы с помощью различных приёмов | 3 | 2 | П | 2 | 10 |
| 14 | Умение решать уравнения, неравенства и системы с помощью различных приёмов | 3 | 2 | П | 2 | 15 |
| 15 | Умение моделировать реальные ситуации на языке математики; составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат; умение решать тестовые задачи разных типов, в том числе задачи из области управления личными и семейными финансами | 6 | 1-3 | П | 2 | 25 |
| Всего заданий – 15; из них по типу заданий: с кратким ответом – 12, с развернутым ответом – 3; По уровню сложности: Б – 75, П – 8. Максимальный первичный балл за работу – 18. Общее время выполнения работы: 2 часа 30 минут (150 минут) |
Вариант 1
Часть 1
Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.
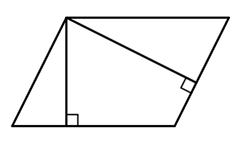
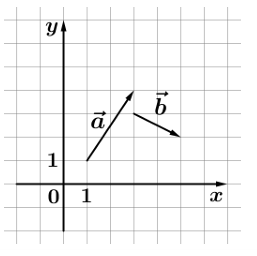
На координатной плоскости изображены вектора 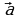 и
и 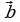 , координатами которых являются целые числа. Найдите скалярное произведение
, координатами которых являются целые числа. Найдите скалярное произведение 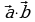 .
.
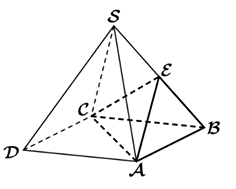
Объем правильной четырехугольной пирамиды SABCD равен 116. Точка Е – середина ребра SB. Найдите объем треугольной пирамиды ЕАВС.
В чемпионате по гимнастике участвуют 25 спортсменок: 6 из Венгрии, 7 из Румынии, остальные из Болгарии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Болгарии.
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,96. Вероятность того, что масса окажется больше 790 г, равна 0,82. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Найдите корень уравнения: 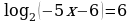
Найдите значение выражения: 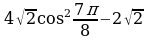
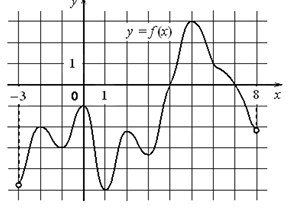
На рисунке изображен график функции 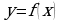 , определенной на интервале
, определенной на интервале 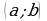 . Найдите количество точек, в которых производная функции
. Найдите количество точек, в которых производная функции 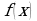 равна 0.
равна 0.
К источнику с ЭДС 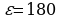 В и внутренним сопротивлением
В и внутренним сопротивлением 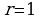 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле
Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле 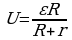 . При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В? Ответ дайте в Омах.
. При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В? Ответ дайте в Омах.
От пристани А к пристани В, расстояние между которыми равно 240 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью на 1 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
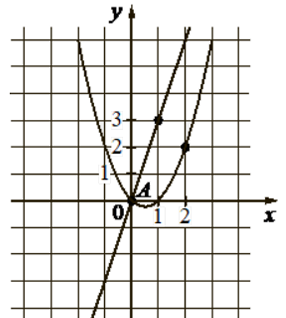
На рисунке изображены графики функций видов 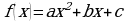 и
и 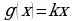 , пересекающиеся в точках А и В. Найдите абсциссу точки В.
, пересекающиеся в точках А и В. Найдите абсциссу точки В.
Найдите точку минимума функции 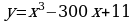 .
.
Часть 2
а) Решите уравнение: 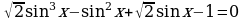
б) Найдите все корни этого уравнения, принадлежащие отрезку 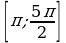 .
.
Решите неравенство: 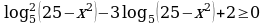 .
.
15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Вариант 2
Часть 1
Стороны параллелограмма равны 9 и 15. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите высоту, опущенную на большую сторону параллелограмма.

На координатной плоскости изображены вектора 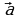 и
и 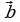 , координатами которых являются целые числа. Найдите скалярное произведение
, координатами которых являются целые числа. Найдите скалярное произведение 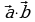 .
.
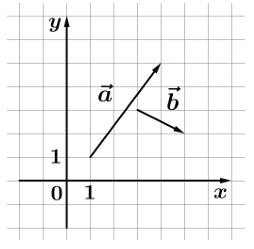
Объем правильной четырехугольной пирамиды SABCD равен 152. Точка Е – середина ребра SB. Найдите объем треугольной пирамиды ЕАВС.

В чемпионате по гимнастике участвуют 50 спортсменок: 13 из
Великобритании, 7 из Франции, остальные из Германии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность
того, что спортсменка, выступающая первой, окажется из Германии.
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,98. Вероятность того, что масса окажется больше 790 г, равна 0,83. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Найдите корень уравнения: 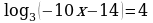
Найдите значение выражения: 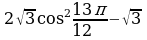
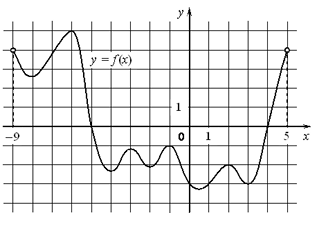
На рисунке изображен график функции 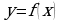 , определенной на интервале
, определенной на интервале 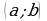 . Найдите количество точек, в которых производная функции
. Найдите количество точек, в которых производная функции 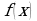 равна 0.
равна 0.
К источнику с ЭДС 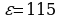 В и внутренним сопротивлением
В и внутренним сопротивлением 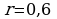 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле
Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле 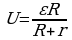 . При каком значении сопротивления нагрузки напряжение на ней будет равно 100 В? Ответ дайте в Омах.
. При каком значении сопротивления нагрузки напряжение на ней будет равно 100 В? Ответ дайте в Омах.
От пристани A к пристани B, расстояние между которыми равно153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.
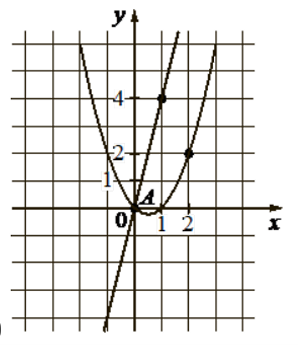
На рисунке изображены графики функций видов 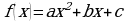 и
и 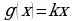 , пересекающиеся в точках А и В. Найдите абсциссу точки В.
, пересекающиеся в точках А и В. Найдите абсциссу точки В.
Найдите точку минимума функции 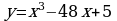 .
.
Часть 2
а) Решите уравнение: 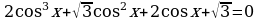
б) Найдите все корни этого уравнения, принадлежащие отрезку 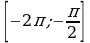 .
.
Решите неравенство: 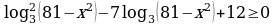 .
.
15-го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Приложение
Система оценивания экзаменационной работы по математике
Правильное выполнение каждого из заданий 1–12 оценивается 1 баллом. Задание считается выполненным верно, если ответ записан в той форме, которая указана в инструкции по выполнению задания, и полностью совпадает с эталоном ответа.
| Номер задания | Правильный ответ |
| 1 вариант | 2 вариант |
| 1. | 1,5 | 6 |
| 2. | 1 | 2 |
| 3. | 29 | 38 |
| 4. | 0,48 | 0,6 |
| 5. | 0,78 | 0,81 |
| 6. | -14 | -9,5 |
| 7. | 2 | 1,5 |
| 8. | 7 | 9 |
| 9. | 17 | 4 |
| 10. | 15 | 9 |
| 11. | 4 | 5 |
| 12. | 10 | 4 |
Критерии оценивания выполнения заданий с развёрнутым ответом
Задание 13
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | 2 |
| Обоснованно получен верный ответ в пункте а ИЛИ Получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Задание 14
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ. | 2 |
| Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Задание 15
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Процентное соотношение выставления отметки за экзаменационную работу
| Уровень | Общий % выполнения работы | Количество баллов | Отметка |
| Повышенный | 90-100% | 17-18 | «5» |
| Прочный базовый | 66-89% | 12-16 | «4» |
| Базовый | 50-65% | 7-11 | «3» |
| Недостаточный | 49% и ниже | 0-6 | «2» |







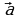 и
и 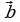 , координатами которых являются целые числа. Найдите скалярное произведение
, координатами которых являются целые числа. Найдите скалярное произведение 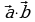 .
.

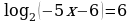
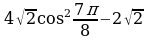
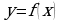 , определенной на интервале
, определенной на интервале 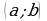 . Найдите количество точек, в которых производная функции
. Найдите количество точек, в которых производная функции 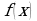 равна 0.
равна 0.
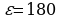 В и внутренним сопротивлением
В и внутренним сопротивлением 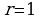 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле
Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле 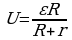 . При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В? Ответ дайте в Омах.
. При каком значении сопротивления нагрузки напряжение на ней будет равно 170 В? Ответ дайте в Омах. 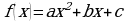 и
и 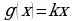 , пересекающиеся в точках А и В. Найдите абсциссу точки В.
, пересекающиеся в точках А и В. Найдите абсциссу точки В.
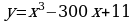 .
.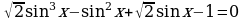
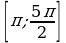 .
.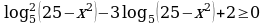 .
.
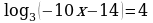
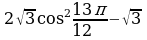

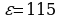 В и внутренним сопротивлением
В и внутренним сопротивлением 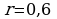 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле
Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле 
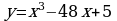 .
.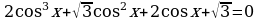
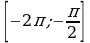 .
.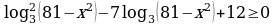 .
.









