Разработка внеклассного мероприятия
на тему «Фрактальные кривые, их характеристика и применение»
Ярославль
2018 г.
Пояснительная записка.
Элективный курс разработан в рамках реализации Концепции пред профильного обучения на средней ступени общего образования и соответствует государственному стандарту среднего образования по математике. При разработке данного курса учитывалось, что элективный курс как компонент образования должен быть направлен на удовлетворение потребностей и интересов десятиклассников, на формирование у них новых видов познавательной и практической деятельности.
Одной из самых важных целей преподавания геометрии является формирование и развитие у учащихся пространственных представлений, а также способности и умения производить операции над пространственными объектами. Достижение этой цели важно не только для тех учащихся, которые в дальнейшем посвятят себя техническим профессиям, но и для тех, кто выберет специальности художника, дизайнера, модельера, хирурга, астронома и других. Слабое развитие пространственных представлений затрудняет изучение ряда учебных дисциплин, а в деятельности взрослого человека может стать причиной многих неудач. Например, конструктору этот недостаток может помешать реализовать творческие планы. Систематическая работа над формированием и развитием пространственных представлений приводит к их улучшению даже при наличии средних природных данных.
Знакомство с современными направлениями развития математики, новыми теоретическими методами исследований, использованием компьютерных программ и технологий для решения учебных и научных задач может осуществляться в рамках факультативов, которые открывают большие возможности для реализации познавательных интересов учащихся и развития личности в целом. В этом случае большую помощь школьному учителю может оказать привлечение к разработке и проведению занятий преподавателей, аспирантов и студентов университетов. Такие курсы могут быть организованы не только в виде факультативов, но и в летних математических школах, школах для одаренных детей и т.д.
Выбор темы факультатива определило то, что фракталы являются одним из молодых и бурно развивающихся разделов математики, который имеет широкий спектр приложений во многих областях, как математики, так и физики, биологии, медицины, геологии, психологии, экономики и др.
Цели курса:
углубить теоретическое и практическое содержание курса фрактальная геометрия;
развивать пространственные представления и логическое мышление;
развивать умение применять знания на практике, в новой ситуации, приводить аргументированное решение, анализировать условие задачи и выбирать наиболее рациональный способ ее решения.
Задачи курса:
познакомиться с фракталами, их многообразием и классификацией;
изучить методы построения геометрических фракталов;
решить задачи на построение фракталов с помощью L-кодов;
решить задачи на построение фракталов геометрическим способом;
Все занятия направлены на расширение и углубление базового курса. Содержание курса можно варьировать с учетом склонностей, интересов и уровня подготовленности учеников.
Основной тип занятий - практикум. Для наиболее успешного усвоения материала планируются различные формы работы с учащимися: лекционно-семинарские занятия, групповые, индивидуальные формы работы. Для текущего контроля на каждом занятии учащимся рекомендуется серия заданий, часть которых выполняется в классе, а часть - дома самостоятельно.
Тематическое планирование
| Тема занятия
| Количество часов |
Форма проведения |
| Обзорная лекция | 2 | Лекция |
| Снежинка Коха Площадь снежинки Коха Длина дуги Непрерывность Дифференцируемость Размерность | 2 | Практика |
| Ковер Серпинского | 2 | Практика |
| Губка Менгера Площадь губки Менгера Периметр Непрерывность Дифференцируемость Размерность | 2 | Практика |
Вводная лекция по теме «Фракталы»
«Фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
Является самоподобной или приближённо самоподобной.
Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Сообщение на тему «Мандельброт-отец современной фрактальной геометрии» (отвечает 1 ученик)
Классификация
Фракталы делятся на группы. Самые большие группы это:
* геометрические фракталы
* алгебраические фракталы
* системы итерируемых функций
* стохастические фракталы.
Геометрические фракталы.
Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.
Алгебраические фракталы (Проект «Алгебраические фракталы»)
Множество Мандельброта
Множество Жюлиа
Треугольники Серпинского
Геометрические фракталы (Проект «Геометрические фракталы»)
Кривая Коха (снежинка Коха)
Кривая Леви
Кривая Гильберта
Ломаная (кривая) дракона (Фрактал Хартера-Хейтуэя)
Множество Кантора
Дерево Пифагора
Круговой фрактал
Стохастические фракталы ( Проект «Стохастические фракталы»)
В течение последующих двадцати лет метод фазового пространства использовался для исследования множества сложных систем. Каждый раз ученые и математики составляют нелинейные уравнения, решают их численными методами, а компьютеры вычерчивают решения в виде траекторий в фазовом пространстве. К своему великому удивлению, исследователи обнаружили, что число различных аттракторов весьма ограничено. Их формы можно классифицировать топологически, а общие динамические свойства системы — вывести из формы ее аттрактора.
Существует три основных типа аттракторов: точечные, соответствующие системам, которые достигают устойчивого равновесия; периодические, соответствующие периодическим колебаниям; и так называемые странные аттракторы, соответствующие хаотическим системам. Типичный пример системы со странным аттрактором представляет собой «хаотический маятник», впервые исследованный японским математиком Йошисуке Уэда в конце 1970-х годов. Это нелинейная электронная схема с внешним питанием, относительно простая, но с исключительно сложным поведением. Каждое колебание этого хаотического генератора колебаний уникально. Система никогда не повторяет себя, и каждый цикл открывает новую область фазового пространства. Тем не менее, несмотря на кажущуюся неустойчивость движения, точки в фазовом пространстве расположены отнюдь не беспорядочно. Вместе они формируют сложный высокоорганизованный паттерн — странный аттрактор, который теперь носит имя Уэда.
 Аттрактор Уэда.
Аттрактор Уэда.
Аттрактор Уэда — это траектория в двухмерном фазовом пространстве, которая образует почти повторяющие друг друга паттерны. Это типичная особенность хаотических систем. Изображение на рис. 6-10 содержит более 1 000 000 точек. Ее можно представить в виде среза куска теста, который многократно растягивали и сворачивали. Это означает, что в основе аттрактора Уэда лежит математика преобразования пекаря.
Одно удивительное свойство странных аттракторов заключается в том, что они, как правило, ограничены малым числом измерений — даже в многомерном фазовом пространстве. Например, система может содержать 50 переменных, но ее движение при этом описывается трехмерным странным аттрактором — свернутой поверхностью в 50-мерном пространстве. Это, естественно, характеризует высокую степень порядка.
Таким образом, хаотичное поведение — в современном научном понимании этого термина — разительно отличается от беспорядочного, неустойчивого движения. С помощью странных аттракторов можно определить различие между обычной беспорядочностью, или шумом, и хаосом. Хаотичное поведение детерминировано и образует паттерны, а странные аттракторы позволяют преобразовывать на первый взгляд случайные данные в отчетливые визуальные формы.
В работах некоторых математиков ранее была установлена возможность существования странных аттракторов, впервые построение странного аттрактора (рис. 2) как решение системы дифференциальных уравнений осуществил в работе по компьютерному моделированию термоконвекции и турбулентности в атмосфере американский метеоролог Э. Лоренц (E.Lorentz, 1963). Конечное состояние системы Лоренца чрезвычайно чувствительно к начальному состоянию. Сам же термин «странный аттрактор» появился позже, в работе Д. Рюэлля и Ф. Такенса в (D.Ruelle, F. Takens, 1971: см. Рюэль, 2001) о природе турбуленции в жидкости; авторы отмечали, что размерность странного аттрактора отлична от обычной, или топологической.Позже Б. Мандельброт (B.Mandelbrot) отождествил странные аттракторы, траектории которых при последовательных вычислениях компьютера бесконечно расслаиваются, расщепляются, с фракталами.
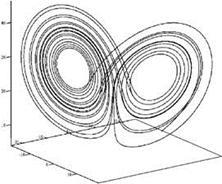

Рис. 2. (Хаотические траектории в системе Лоренца). Аттрактор Лоренца (Кроновер, 2000)
Лоренц (Lorenz, 1963) обнаружил, что даже простая система из трех нелинейных дифференциальных уравнений может привести к хаотическим траекториям В свою очередь, движение воздушных потоков в плоском слое жидкости постоянной толщины при разложении скорости течения и температуры в двойные ряды Фурье с последующем усечением до первых-вторых гармоник:

где s, r и b -- некоторые положительные числа, параметры системы. Обычно исследования системы Лоренца проводят при s =10, r =28 и b =8/3 (значения параметров).
Таким образом, системы, поведение которых детерминируется правилами, не включающим случайность, с течением времени проявляют непредсказуемость за счет нарастания, усиления, амплификации малых неопределенностей, флуктуаций. Наглядный образ системы с нарастанием неопределенности - так называемый биллиард Я.Г. Синая: достаточно большая последовательность соударений шаров неизбежно ведет к нарастанию малых отклонений от исчисляемых траекторий (за счет не идеально сферической поверхности реальных шаров, не идеально однородной поверхности сукна) и непредсказуемости поведения системы.
«преобразование пекаря» с последовательным растягиванием и складыванием, бесконечным образованием складок - одна из моделей возникновения перехода от порядка к хаосу; при этом число преобразований может служить мерой хаоса. Есть Аттрактор Айдзавы, который является частным случаем аттрактора Лоренца.

где а = 0,95, B = 0,7, с = 0,6, d = 3,5, е = 0,25, F = 0,1. Каждая предыдущая координата вводится в уравнения, полученное в результате значение , умноженное на значения времени.

Примеры других странных аттракторов
Аттрактор ВангСун
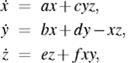
Здeсь a, b, d, e?R, c 0 и f

Аттрактор Рёсслера

, где a,b,c= положительные постоянные. При значениях параметров a=b=0.2 и

Размерности аттракторов
Отличительная особенность странных аттракторов состоит в наличии свойства масштабной инвариантности (скейлинга), выражающегося в повторяемости их структуры на все более мелких масштабах. Следствием закономерностей подобия является универсальность в геометрии хаотических множеств сечений Пуанкаре, в распределении энергии колебаний по частотам и амплитудам в спектре и т.д. Для характеристики странных аттракторов введено понятие размерности. Размерность определяет количество информации, необходимое для задания координат точки, принадлежащей аттрактору, в рамках указанной точности. Для регулярных аттракторов, являющихся многообразиями, размерность – целое число: неподвижная точка имеет размерность 0, предельный цикл – 1, двумерный тор – 2. Ввиду сложности геометрической структуры странные аттракторы не являются многообразиями и имеют дробную размерность. Определения размерности в общем разделяются на два типа: зависящие только от метрических свойств аттрактора и, помимо метрики, зависящие от статистических свойств потока, обусловленных динамикой. В типичных случаях метрические размерности принимают одинаковую величину, которую принято называть фрактальной размерностью аттрактора D. Размерность, определяемую с учетом вероятности посещения траекторией различных областей аттрактора в фазовом пространстве, называют информационной или размерностью натуральной меры.



Ляпуновская размерность
Фрактальную размерность аттрактора ДС в фазовом пространстве R^N можно оценить с помощью спектра ляпуновских характеристических показателей (ЛХП). Такая оценка называется ляпуновской размерностью D L и задается определенным соотношением, называемым формулой Каплана-Йорке. Пусть известен спектр ЛХП странного аттрактора N-мерной системы, размерность которого нужно оценить: 1 2 … N. Сумма всех показателей спектра отрицательна в силу диссипативности системы. Рассмотрим первые k показателей спектра ЛХП, где k – наибольшее число, удовлетворяющее условию В указанное число показателей включены все положительные, все нулевые и некоторая часть отрицательных, чтобы сумма оставалась неотрицательной. Поскольку сумма показателей задает характер локального изменения элемента фазового объема в аттракторе, то фазовый объем размерности k
25Таким образом, можно предположить, что размерность аттрактора заключена в интервале k D L k + 1. Разумно потребовать, чтобы движение на аттракторе подчинялось условию, отвечающему физическим представлениям о стационарности процесса, где d – дробная часть размерности. Полная ляпуновская размерность аттрактора будет суммой целой k и дробной d частей. Различия в сигнатуре спектров ЛХП и размерность D L могут быть признаком классификации регулярных и странных аттракторов. Из формулы Каплана-Йорка для регулярных аттракторов получаем следующие значения ляпуновской размерности, совпадающие с фрактальной размерностью соответствующего множества и равные числу нулевых показателей в спектре ЛХП:
состояние равновесия (-, -, -, …) – D L = 0;
предельный цикл (0, -, -, -, …) – D L = 1;
двумерный тор (0, 0, -, -, …) – D L = 2;
N-мерный тор (0, 0, 0, …,0, -, …) – D L = N.
Для регулярных аттракторов в полном соответствии находятся: ляпуновская размерность, фрактальная размерность и сигнатура спектра ЛХП аттрактора. В отношении странных аттракторов о подобном взаимодействии можно говорить лишь применительно к трехмерным дифференциальным системам и двумерным обратимым отображениям с постоянным растяжением и сжатием. Было доказано, что для аттракторов в таких системах фрактальная размерность может быть определена следующими соотношениями: - для двумерных отображений - для трехмерных дифференциальных систем В общем случае имеет место следующее соотношение между размерностями: Однако в пределах ошибок вычислений можно приближенно считать, что значения размерностей совпадают. При выборе, каким определением размерности лучше воспользоваться, обычно исходят из возможностей численных расчетов. При численном моделировании ДС наиболее удобно использовать размерность Ляпунова. Для оценки фрактальной размерности аттрактора по экспериментальным данным лучше всего подходит корреляционная размерность.
Развитие теории динамических систем во второй половине ХХ века привело к грандиозным последствиям не только в теоретической физике и математике, но и в естествознании в целом -- открытию динамического хаоса и связанными с ним свойствами. Оказалось, что многие нелинейные системы, несмотря на полную детерминированность, т.е. отсутствие шумов, стохастических возмущений и т.п., могут демонстрировать поведение, подобное случайным процессам. Тем самым возникающая статистика поведения систем определяется исключительно особенностями динамики. И хотя предпосылки такой идеологии наметились еще более ста лет назад в работах А.М.Ляпунова и А.Пуанкаре, основные открытия и осмысление этого явления были сделаны в 60-80-х годах прошлого века. Необходимо отметить, что для изучения хаотических систем классические аналитические средства, такие, например, как ряды теории возмущений, асимптотические методы и т.п., оказались непригодными. Так, подкову Смейла, с которой в известном смысле началось современное исследование хаотических явлений, невозможно описать соотношениями в математическом стиле XIX века. Для построения и анализа таких конструкций потребовалось разработать совершенно новые методы, развитие которых и привело к крупным открытиям в теории динамических систем.
ПЛАН-КОНСПЕКТ ЭЛЕКТИВНОГО ЗАНЯТИЯ
Тема занятия: Снежинка Коха
Тип занятия: изложение нового материала, повторения
Форма проведения: комбинированное занятие
Цели занятия:
1. Образовательная:
формирование знаний о фрактальной кривой – Снежинка Коха, изучение площади, длины дуги, непрерывности, дифференцируемости, размерности Снежинки Коха.
2. Воспитательная:
создать условия, обеспечивающие формирование у учеников навыков самоконтроля, обеспечить высокую активность при выполнении задания.
3. Развивающая:
развитие речи, мышления; умственная деятельность: анализ, синтез, классификация, способность наблюдать, делать выводы, выделять существенные признаки объектов, умение выделять цели и способы деятельности, проверять ее результаты, выдвигать гипотезы.
Оборудование к уроку:
Инструкция для обучающихся
ХОД УРОКА:
изложение нового материала:
| Этап занятия | время (мин) | Действия учителя | Деятельность обучающихся | УУД |
|
Организационный момент
|
1-2 мин
| Проверяет готовность обучающихся к занятию. Озвучивает тему и цель урока. - Здравствуйте, ребята. Садитесь. Сегодня мы с вами начнем изучать фрактальные кривые, а именно рассмотрим Снежинку Коха. | Учащиеся сообщают кого нет на занятии, заслушивают тему занятия. | Регулятивные УУД: самостоятельно организовывают свое рабочее место |
| Этап актуализации знаний | 2 мин | На прошлом занятии мы с вами познакомились с классическими фрактальными кривыми, заслушали ваши доклады, давайте вспомним, что вы узнали в прошлый раз и ответим на несколько вопросов. Кто был родоначальником понятия фрактал? (Бенуа Мандельброт) Как вы поняли, что же такое фрактал? (Фрактал – термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.) На какие группы делятся фракталы? (геометрические, алгебраические, системы итерируемых функций, стохастические)
| Учащиеся отвечают на вопросы учителя, вспоминают материал, изученный ранее. Примерные ответы учеников: Бенуа Мандельброт Фрактал – термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. геометрические, алгебраические, системы итерируемых функций, стохастические | Коммуникативные УУД: участвовать в диалоге, высказывать свою точку зрения, оформлять свои мысли в устной речи. Регулятивные УУД: определять цель учебной деятельности. Познавательные УУД: определять круг своего незнания, самостоятельно делать выводы, перерабатывать информацию.
|
| Изложение нового материала
| 30-35 мин | Чтобы приступить к изучению нашей темы, давайте разделимся на 5 групп. Сегодня вы будете самостоятельно добывать новые знания. Для каждой группы будет свое задание, затем как вы его выполните, мы будем обсуждать ваши полученные результаты и представлять другим. Итак, первая группа сегодня будет вычислять площадь Снежинки Коха, вторая группа будет заниматься длиной дуги, третья изучит непрерывность, четвертая группа рассмотрит дифференцируемость и пятая группа будет заниматься размерностью Снежинки Коха. Вам будет выдана инструкция с ходом действий, теоретическим материалом. | Учащиеся приступают к делению на группы, работают с выданной им инструкцией, выполняют поставленное задание. Составляют опорные конспекты, находят в тексте понятия, информацию. | Коммуникативные УУД: участвовать в работе группы, распределять роли, договариваться друг с другом, слушать и понимать других, читать про себя информацию и понимать прочитанное. Познавательные УУД: перерабатывать, систематизировать информацию, выбирать нужную информацию. Регулятивные УУД:самостоятельно организовывать рабочее место в соответствии с целью выполнения заданий, определять цель учебной деятельности, план выполнения задания, самоконтроль.
|
| Первичное закрепление
| 10 мин | Давайте посмотрим, что у вас получилось сделать. По очереди по одному из представителей группы выйдут и расскажут всем, что получилось. Остальные записывают полученное в тетради. | Рассказывают о том, что у них получилось, формулируют свои выводы. Слушают доклады, делятся впечатлениями. | Познавательные УУД: систематизировать информацию, выбирать нужную информацию. Регулятивные УУД: Самоконтроль и коррекция.
|
| Самоанализ и самоконтроль.
| 5 мин | Мы заслушали ответы всех групп, теперь давайте подведем итоги, сделаем выводы. | Анализируют проделанную работу, высказывают свое мнение. | Познавательные УУД: систематизировать информацию, выбирать нужную информацию. Регулятивные УУД: Самоконтроль и коррекция.
|
| Подведение итогов занятия
| 3 мин | Итак, сегодня мы изучили такую фрактальную кривую как Снежинка Коха, какие вопросы у вас есть? Какие моменты остались непонятными? (Если вопросы остались, то учитель отвечает на них) Запишите домашнее задание. | Задают вопросы по информации, которая им осталась непонятной, формулируют конечный результат своей работы на занятии.
| Коммуникативные УУД: участвовать в коллективном обсуждении, осуществлять контроль. Познавательные УУД: выполнять логические операции: сравнивать, синтезировать, классифицировать Регулятивные УУД: способность к преодолению препятствий, оценивать результаты своей и чужой деятельности, самоконтроль, самооценка.
|
Домашнее задание: еще раз просмотреть изученный материал на занятии, найти и изучить информацию про Ковер Серпинского.
Пример инструкции.
Теоретический материал
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.

Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии.
 Формула суммы геометрической прогрессии:
Формула суммы геометрической прогрессии:

Задание: Найти площадь Снежинки Коха.
Теоретический материал про снежинку Коха
Основные свойства кривой Коха
1. Она непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана — как пример такого рода математических «уродцев».
2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.

3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно — снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний — формулы площади треугольника и суммы геометрической прогрессии проходят в школе. Для интересующихся вычисление приведено ниже мелким шрифтом.
Пусть сторона исходного правильного треугольника равна a. Тогда его площадь  . Сначала сторона равна 1, а площадь:
. Сначала сторона равна 1, а площадь:  . Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n-м шаге будет достроено Tn = 3 · 4n–1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3)n. Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна
. Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n-м шаге будет достроено Tn = 3 · 4n–1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3)n. Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна  . При больших значениях n это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равенTn · Sn = 3/4 · (4/9)n · S0. Поэтому после n-го шага площадь фигуры будет равна сумме S0 + T1 · S1 + T2 · S2 + ... +Tn · Sn =
. При больших значениях n это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равенTn · Sn = 3/4 · (4/9)n · S0. Поэтому после n-го шага площадь фигуры будет равна сумме S0 + T1 · S1 + T2 · S2 + ... +Tn · Sn =  . Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула:
. Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула:  . Площадь снежинки равна
. Площадь снежинки равна .
.
4. Фрактальная размерность равна log4/log3 = log34 ≈ 1,261859... . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности. Из формулы степенной зависимости N(δ) ~ (1/δ)D, где N — число пересекающихся квадратиков, δ — их размер, D — размерность, получаем, что D = log1/δN. Это равенство верно с точностью до прибавления константы (одной и той же для всех δ). На рисунках изображена пятая итерация построения кривой Коха, зеленым закрашены квадратики сетки, которые с ней пересекаются. Длина исходного отрезка равна 1, поэтому на левом рисунке длина стороны квадратиков равна 1/9. Закрашено 12 квадратиков, log912 ≈ 1,130929... . Пока не очень похоже на 1,261859... . Смотрим дальше. На среднем рисунке квадратики в два раза меньше, их размеры 1/18, закрашено 30. log1830 ≈ 1,176733... . Уже лучше. Справа квадратики еще вдвое меньше, закрашено уже 72 штуки. log7230 ≈ 1,193426... . Еще ближе. Дальше нужно увеличивать номер итерации и одновременно уменьшать квадратики, тогда «эмпирическое» значение размерности кривой Коха будет неуклонно приближаться к log34, а в пределе и вовсе совпадет.

Варианты
 Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника. Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°. Квадратный вариант. Тут достраиваются квадраты.
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника. Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°. Квадратный вариант. Тут достраиваются квадраты.
Граф согласования






Список литературы.
Р.М. Кроновер. Фракталы и хаос в динамических системах. Основы теории. Москва: Постмаркет, 2000.-352 с.
http://ru.wikipedia.org/wiki/фрактал
http://ghcube.com/
Мандельброт Б. Фрактальная геометрия природы.
Третьяков Ю.Д. Дендриты, фракталы и материалы // Соросовский образовательный журнал.
http://www.fractals-main.ru/perelman_page0.html:
http://lol54.ru/education/uvgsfeshshht_informative/28368-ogromnaja-podborka-fraktalov-fractals-176-sht..html
http://ru.wikipedia.org/wiki/%D4%F0%E0%EA%F2%E0%EB. http://3dfractal.ru/stati-o-fraktalah/31.html






 Аттрактор Уэда.
Аттрактор Уэда.




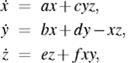







 Формула суммы геометрической прогрессии:
Формула суммы геометрической прогрессии:


 Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника. Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°. Квадратный вариант. Тут достраиваются квадраты.
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника. Линии Чезаро. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°. Квадратный вариант. Тут достраиваются квадраты. 









