Просмотр содержимого документа
«Электромагнитные колебания и волны»

Электромагнитные колебания и волны
- Свободные электромагнитные (ЭМК) в колебательном контуре.
- Виды нагрузок в цепи переменного тока (активная, емкостная, индуктивная).
- Полное сопротивление в цепи переменного тока.
- Электрический резонанс. (Добротность контура).

1. Свободные электромагнитные колебания(ЭМК)
- Периодические гармонические изменения электрических величин: q(t), u(t), i(t),e(t), ф (t), …
- Мгновенные значения электрических величин q(t), u(t), i(t) определяются:
q(t)= q 0 cos( ω t+ φ 0 ) , q 0
u(t)= u 0 cos( ω t+ φ 0 ), u 0 =q 0 /с
i (t)= q '(t)= - q 0 ω sin( ω t+ φ 0 )= = i 0 cos( ω t+ φ 0 + π / 2 ), i 0 =q 0 ω
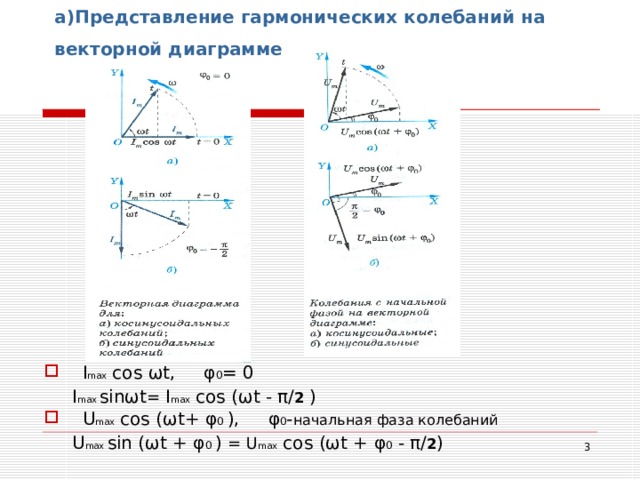
а)Представление гармонических колебаний на векторной диаграмме
I max sin ω t = I max cos ( ω t - π / 2 )
- U max cos ( ω t+ φ 0 ) , φ 0 - начальная фаза колебаний
U max sin ( ω t + φ 0 ) = U max cos ( ω t + φ 0 - π / 2 )

б) Свободные ЭМК в колебательном контуре(КК)
КК – устройство, включающее последовательно соединенные конденсатор c электроемкостью С и катушку c индуктивностью L . В идеальном случае R =0 (идеальный КК).

в)Преобразование энергии в колебательном контуре(КК)
- Периодические изменения потенциальной энергии заряженного конденсатора Wp и энергии магнитного поля катушки Wm .
W = W p +W m = const
W = W p max = const
W = W m max =const


Преобразование энергии в колебательном контуре(КК)
- t=0 Конденсатор заряжен, ток в катушке отсутствует.
W p = max , W m =0
Конденсатор начинает разряжаться, ток в катушке нарастает постепенно (ЭМИ препятствует току) до W m max .
W = W p +W m = const
- t= Т/4 Конденсатор разряжен, ток в катушке максимальный, противоположный по знаку.
W p = 0 , W m = max
Конденсатор начинает перезаряжаться, ток в катушке убывает постепенно (ЭМИ поддерживает) до Wp max .
W = W p +W m = const

Преобразование энергии в колебательном контуре(КК)
- t= Т/2 Конденсатор полностью перезарядился (знак заряда противоположный первоначальному), ток в катушке уменьшился до 0.
W p = max , W m = 0
Процессы начинают протекать аналогично в обратном направлении. Система возвращается в первоначальное состояние.
При отсутствии потерь в КК совершаются незатухающие ЭМК заряда на обкладках конденсатора и силы тока в катушке индуктивности.

Частота и период собственных гармонических колебаний в КК
Из закона сохранения
энергии
W = Wp+Wm = const
частота и период собственных колебаний в КК определяется формулой У.Томсона
(полученной в 1853 г.)

2.Виды нагрузок в цепи переменного тока (таблица)
- Активная (активное сопротивление) – резистор с сопротивлением R
- Емкостная (емкостное сопротивление) – конденсатор с электроемкостью c
- Индуктивное (реактивное сопротивление) – катушка индуктивности L

Таблица «Виды нагрузок в цепи переменного тока»
- Схема подключения нагрузки
- Законы изменения u(t), i(t)
- Амплитудные значения u 0 , i 0
- Сопротивление нагрузки и график зависимости сопротивления от циклической частоты ω
- Графики зависимости u(t), i(t)
- Векторные диаграммы, характеризующие сдвиг фаз между колебаниями u(t), i(t)

а)Активное сопротивление R

б)Емкостное сопротивление Хс

в)Индуктивное (реактивное) сопротивление Х L

Действующие значения силы тока и напряжения в цепи переменного тока и среднюю мощность переменного тока фиксируют измерительные приборы
- Действующие (эффективные) значения силы тока и напряжения в цепи переменного тока равны значениям силы постоянного тока и напряжения, при которых в проводнике выделяется такое же количество теплоты за одинаковый промежуток времени
I д = i 0 /√2 U д = U 0 /√2
- Средняя мощность переменного тока равна мощности, выделяющейся при протекании по резистору R постоянного тока:
Р ср = I д ² R= i 0 ² R / 2
На конденсаторе и катушке средняя мощность за период переменного тока равна 0 .

3. Полное сопротивление в цепи переменного тока
- В реальном КК потери энергии на сопротивлении R компенсируют, подключая в электрическую цепь генератор переменного тока.

4. Резонанс в цепи переменного тока
- Резонанс - явление резкого возрастания амплитуды колебаний при совпадении частоты вынуждающей силы и собственной частоты колебаний системы.
- В КК – резкое возрастание амплитуды силы тока при равенстве U C = -U L
- Х С =Х L
- Добротность Q характеризует возможные потери энергии в КК в зависимости от его характеристик

Домашнее задание
- Лекция – записи
- Обобщающая таблица «Виды нагрузок в цепи переменного тока»
- ФМШ № - по группам



































