Электронная математическая газета "Занимательное в мире математики"

Электронная математическая газета «Занимательное в мире математики»

Многие из нас думают, что математика скучная и сложная. Но что если это не так?

Руководитель Мамасуева Т.П.

Подготовили учащиеся 8Ж класса

Содержание

1. Занимательные задачи (Сколько лет? Кирпичик)

2. Пятое математическое действие (занимательная задача « Четырьмя единицами»)

3. Числовые великаны( Упражнения с миллионом, Названия числовых великанов: миллиард, триллион, числа-сверхгиганты, гугол, гуголплекс, гуголбиплекс и гуголтриплекс, число Грэма)

4. Числовые лилипуты(Лилипуты времени)

5 Параболоиды(Эллиптический параболоид, Гиперболический параболоид, Параболический цилиндр)

6. Виды геометрии (Неевклидовые геометрии, Геометрия Лобачевского, Сферическая геометрия, Геометрия Римана)

Сколько лет?

У любителя головоломок спросили, сколько ему лет. Ответ был замысловатый:

— Возьмите трижды мои годы через три года и отнимите трижды мои годы три года назад, — у вас как раз и получатся мои годы.

Сколько же ему теперь лет?

Решение

Через трижды три года загадчик будет на 9 лет старше, чем теперь. Трижды три года назад он был на 9 лет моложе, чем теперь. Разница лет, следовательно, составляет 9 + 9, т.е. 18 лет. Это и есть возраст загадчика, согласно условию задачи.

Но эту же задачу можно решить и алгебраическим способом, составив уравнение. Искомое число лет обозначим буквой х. Возраст спустя 3 года обозначим х + 3, возраст 3 года назад обозначим х - 3. Получим уравнение

3( х + 3) – 3( х - 3) = х ,

Решив которое, получаем х = 18.

Проверим: через 3 года ему будет 21, 3 года назад ему было 15. Разность

3 * 21 – 3 * 15 = 63 – 45 = 18,

т.е. равна нынешнему возрасту любителя головоломок.

Кирпичик

Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 4 раза меньше?

Решение

Ответ, что игрушечный кирпичик весит 1 кг, т. е. всего вчетверо меньше, грубо ошибочен. Кирпичик ведь не только вчетверо короче настоящего кирпича, но и вчетверо уже и вчетверо ниже ; поэтому его объём и вес меньше в 4 * 4 * 4 = 64 раза. Правильный ответ такой:

игрушечный кирпичик весит 4000 : 64 = 62,5 г.

Пятое математическое действие

Поговорим о «пятом действии» – возведении в степень. Мы очень часто сталкиваемся с ним в реальной действительности. Вспомним о многочисленных случаях вычисления площадей и объёмов, где обычно приходится возводить числа во вторую и третью степени. Далее: сила всемирного тяготения, электростатическое и магнитное взаимодействия, свет, звук – ослабевают пропорционально второй степени расстояний.

Таких примеров можно привести массу. Но не надо думать, что практика сталкивает нас со вторыми и третьими степенями, а более высокие показатели существуют только в учебниках и задачниках по алгебре. Например, исследуя силу, с какой текучая вода увлекает камни, гидротехник наталкивается на зависимость шестой степени: если скорость течения в одной реки вчетверо больше, чем в другой, то быстрая река способна перетаскивать по своему ложу в 4^6, т. е. в 4096 раз более тяжёлые, чем медленная.

Четырьмя единицами

Задача: четырьмя единицами, не употребляя никаких знаков математических действий, написать большее число.

Решение: Естественно приходящее на ум число – 1111 – не отвечает требованию задачи, так как число 11 11 во много раз больше. Вычислить это число десятикратным умножением на 11 едва ли у кого хватит терпения. Гораздо быстрее можно оценить его величину с помощью лагорифмических таблиц.

Это число превышает 258 миллиардов и, следовательно, больше числа 11 в 25 с лишним миллионов раз.

Числовые великаны

Начнём с миллиона – старейшего числового великана (слово «миллион», означающее тысячу тысяч, в XIII веке придумал великий итальянский путешественник Марко Поло). Если хотите ощутить истинные размеры миллиона, попробуйте хотя бы представить в чистой тетради миллион точек. Я не предлагаю вам доводить такую работу до конца. Едва ли у кого на это хватит терпения, уже одно начало работы, её медленный ход даст вам почувствовать, что такое «настоящий» миллион.

В Павильоне занимательной науки был нанесён на потолке миллион тёмных кружков. Необозримое поле чёрных точек производило на посетителей сильное впечатление и действительно давало возможность ощутить огромность миллиона.

Вопреки распространённому мнению, невооружённый глаз видит на одном полушарии ночного неба 3,5 тыс. звёзд. Это число в 300 раз меньше миллиона. Небольшой голубой кружок на потолке упомянутого павильона, содержавший 3500 тёмных точек и изображавший ночное небо, наглядно подчёркивал своими скромными размерами огромность подлинного числового великана – т миллиона.

Упражнения с миллионом

Задача: величина обыкновенной комнатной мухи около 7 мм в длину. Какова была бы её длина при увеличении в миллион раз?

Решение: умножив 7 мм на 1 000 000, мы получим 7 км – примерно ширина крупного города. Значит, муха, увеличенная линейно в миллион раз, могла бы покрыть его своим телом!

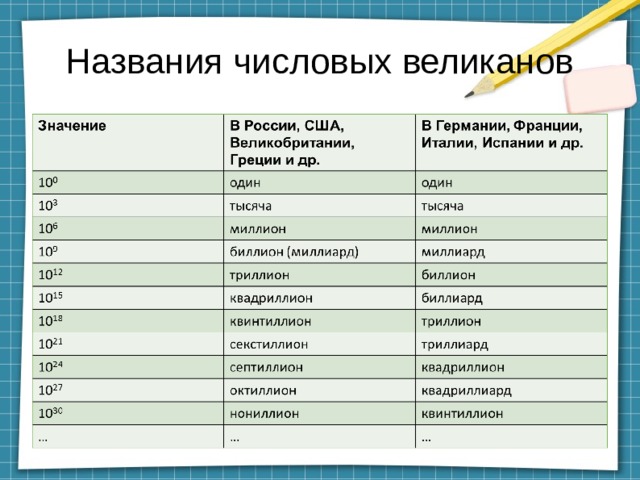
Названия числовых великанов

Миллиард

Миллиард – одно из самых молодых названий чисел. Оно вошло в употребление лишь со времени окончания франко-прусской войны 1871 года, когда французам пришлось уплатить Германии контрибуцию в 5 000 000 000 франков. Как и миллион , слово миллиард происходит от корня «милле» (тысяча) и представляет собою итальянское увеличительное от этого существительного.

Чтобы представить себе огромность миллиарда, подумайте о том, что в «Большой книге занимательных наук» заключается немногим более 300 000 букв. В трёх таких книжках окажется один миллион букв. А один миллиард букв будет заключать в себе стопка из 30 000 экземпляров этой книжки – стопка, которая, будучи аккуратно сложена, составила бы столб высотой с Исаакиевский собор (101 м).

Триллион

Ощутить огромность триллиона трудно даже человеку, привыкшему к обращению с миллионами. Великан-миллион такой же карлик по сравнению с триллионом, как единица по сравнению с миллионом. Многим современным культурным людям эта разница представляется несущественной. По крайней мере они не думают о том, что одно из этих чисел в миллион раз больше другого и что, значит, первое относится ко второму приблизительно так, как расстояние от Москвы до Сан-Франциско относится к ширине улицы.

Волос, увеличенный по толщине в триллион раз, был бы в 8 раз шире земного шара, а муха при таком увеличении была бы в 70 раз толще Солнца!

Числа-сверхгиганты

Число молекул в кубическом сантиметре газа – одно из самых больших множеств, реально исчисленных, – выражается десятками квинтиллионов. Если мы вздумали подсчитать, сколько капель в океане, считая объём капли 1 мм 3 , что весьма мало, нам тогда бы пришлось обратиться к наименованиям выше септиллиона, потому что это число исчисляется только тысячами септиллионов.

И лишь при желании выразить, сколько граммов вещества содержит наша солнечная система, понадобились бы наименования выше септиллиона, так как в этом числе 34 цифры: 2 и 33 нуля, или 2*10 33 .

Гугол

Гугол – число, изображаемое единицей с сотней нулей.

Термин «гугол» не имеет серьёзного теоретического и практического значения. Казнер предложил его для того, чтобы проиллюстрировать разницу между невообразимо большим числом и бесконечностью, и с этой целью термин иногда используется при обучении математике.

Гугол больше, чем количество атомов в известной нам части Вселенной, которых, по разным оценкам, насчитывается от 10 79 до 10 81 , что также ограничивает его применение.

Название компании Google является искажённым написанием слова «гугол» (googol). Создатели известной поисковой машины хотели использовать термин «googol» в качестве названия, но при регистрации выяснилось, что такой домен уже занят. Многие интернет-сервисы компании Google имеют в обратной зоне DNS записи, оканчивающиеся суффиксом «1e100.net», что является вариантом написания числа «гугол» в экспоненциальной нотации (единица, умноженная на 10 в степени 100).

Гуголплекс

Гуголплекс – число, равное 10 гугол (десяти в степени гугол), то есть 10^10 100 . В десятичной записи число можно представить как одна единица и гугол нулей после неё.

Как и гугол, термин «гуголплекс» был придуман американским математиком Эдвардом Казнером и его племянником Мильтоном Сироттой.

Число гугол (а тем более, гуголплекс) больше числа всех частиц в известной нам части вселенной, которое составляет величину от 10 79 до 10 81 .

Гуголбиплекс и гуголтриплекс

С помощью суффикса -плекс образуется число гуголплексплекс (гуголдуплекс или гуголбиплекс) – десять в степени гуголплекс (10^10^10^100).

гуголплексплексплекс (гуголтриплекс) – десять в степени гуголплексплекс (10^10^10^10^100).

Дальше можно образовать такие числа как гуголтетраплекс, гуголпентаплекс, гуголгексаплекс, гуголгептаплекс, гуголоктаплекс, гуголнонаплекс и гуголдекаплекс.

Число Грэма

Число Грэма появилось в работе, посвященной решению одной из задач в теории Рамсея. Задача конечно же довольно надуманная с обывательской точки зрения, хоть и не сильно замороченная, даже легко понятная.

Предлагается взять n-мерный куб, соединить его вершины линиями, и каждое получившееся ребро покрасить одним цветом из двух — либо синим, либо красным.

Суть в том, чтобы понять, до какого значения n можно, по-разному закрашивая рёбра, избежать ситуации, когда одна плоскость в кубе закрашена одним цветом.

(На верхнем изображении показано, как должно быть, на нижнем — как не должно быть)

На самом деле, оно больше любых самых смелых фантазий. Представьте себе цифру, написанную самым мелким шрифтом. Таким мелким, что на атоме можно нарисовать миллионы таких цифр. Представьте себе пространство, заполненное этими цифрами во всех трёх измерениях, вплотную друг к другу. Так вот, места, чтобы вместить десятичную запись числа Грэма, потребуется гораздо больше всей наблюдаемой Вселенной. Мало того, оно не вместится даже в количество Вселенных, равное количеству цифр, помещённых в нашу Вселенную.

Числовые лилипуты

Чтобы их разыскать, не надо прикладывать особых усилий. Достаточно написать ряд чисел, обратных миллиону, миллиарду, триллиону и т. д., т. е. надо делить единицу на эти числа. Это типичные числовые лилипуты. Для них придуман сокращённый способ обозначения. Например, 10 -6 это одна миллионная, 10 -9 это одна миллиардная.

Лилипуты времени

Легко написать 1/1000 секунды, но это – чисто бумажная величина, потому что ничего не может произойти за такой ничтожный промежуток времени.

Так думают многие, но ошибаются, потому что в тысячную долю секунды могут произойти весьма много явлений.

Поезд, проходящий 36 километров в час, делает за секунду 10 метров и, следовательно, в течение 1000-й доли секунды проходит 1 сантиметр. Звук в воздухе переносится в течение 1000-й доли секунды на 34 сантиметра, а пуля, покидающая ружейный ствол со скоростью 700-800 м/с, переносится за тот же промежуток времени на 70 см. Земной шар перемещается каждую 1000-ю долю секунды в своём обращении вокруг Солнца на 30 метров.

Параболоиды

Параболоид – незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

z = tx 2 + uy 2 , где t и u – действительные числа не равные нулю одновременно.

При этом:

• Если t и u одного знака, то параболоид называется эллиптическим . Частный случай эллиптического параболоида, когда t = u, в этом случае поверхность принято называть параболоидом вращения .
• Если t и u разного знака, то параболоид называется гиперболическим .
• Если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром .

Эллиптический параболоид

Эллиптический параболоид – семейство параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.

В декартовых (прямоугольных) координатах задаётся функцией:

z = x 2 /a 2 + y 2 /b 2

Если а = b, то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг оси её симметрии.

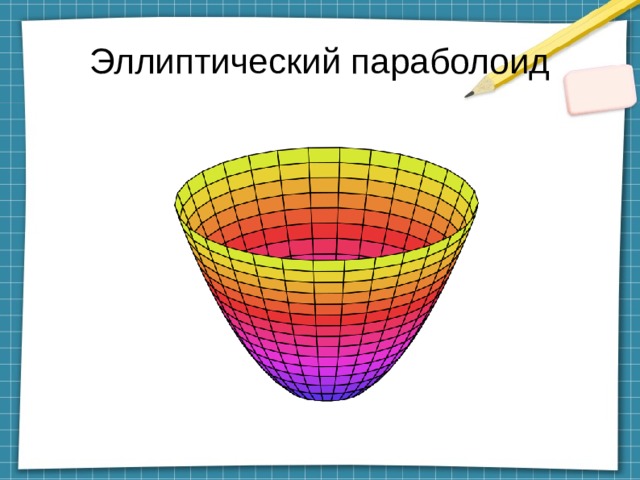
Эллиптический параболоид

Гиперболический параболоид

Гиперболический параболоид — седловая поверхность, описываемая в прямоугольной системе координат уравнением вида

z = x 2 /a 2 - y 2 /b 2 или z = y 2 /b 2 - x 2 /a 2

Также гиперболический параболоид может быть образован движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх.

Гиперболический параболоид

Параболический цилиндр

Параболический цилиндр — цилиндрическая поверхность второго порядка, для которой образующей служит парабола. Её получают при перемещении параболы по направляющей прямой. Тогда следом от параболы будет параболический цилиндр.

В прямоугольной системе координат описывается уравнением

z = ax 2 ,

При а = 0 вырождается в плоскость.

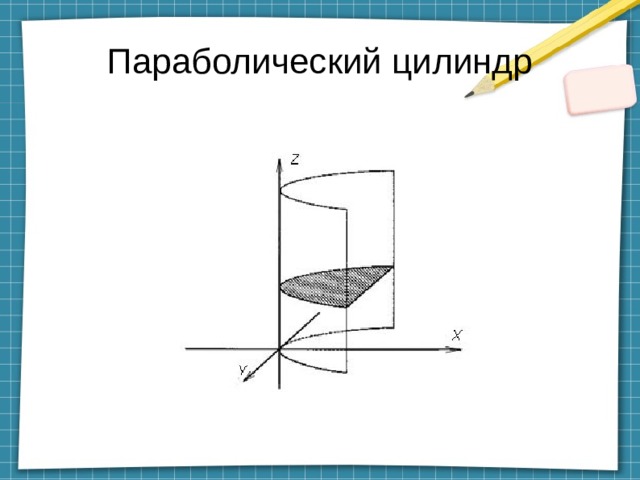
Параболический цилиндр

Неевклидовые геометрии

Неевклидова геометрия  — в буквальном понимании — любая геометрическая система, которая отличается от геометрии Евклида; однако традиционно термин «неевклидова геометрия» применяется в более узком смысле и относится только к традиционным неевклидовым геометрическим системам: геометрии Лобачевского и сферической геометрии (или схожей с ней геометрии Римана).

Геометрия Лобачевского

Геометрия Лобачевского (или гиперболическая геометрия ) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных прямых, которая заменяется её отрицанием.

Евклидова аксиома о параллельных прямых может быть сформулирована так:

На плоскости через точку, не лежащую на данной прямой, можно провести одну, и только одну прямую, параллельную данной.

В геометрии Лобачевского вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Сферическая геометрия

Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы.

Основные положения:

1) Большой круг  — это круг, который делит шар (сферу) на две равные половины. Центр большого круга всегда совпадает с центром сферы. На глобусе, к примеру, все меридианы являются большими кругами. А вот из параллелей только экватор является большим кругом. Все остальные параллели — это малые круги .

2) Кратчайший путь между любыми двумя точками пройдёт по линии большого круга.

3) Через любые две точки на поверхности сферы, кроме диаметрально противоположных, можно провести единственный большой круг. Через диаметрально противоположные точки на сфере можно провести сколько угодно больших кругов.

4) Любые два больших круга пересекаются по прямой, проходящей через центр сферы, а окружности больших кругов пересекаются в двух диаметрально противоположных точках.

5) При пересечении двух больших кругов образуются четыре сферических двуугольника. Площадь двуугольника определяется формулой

S = 2R 2 a , где R — радиус сферы, а а — угол двуугольника в радианах.

6) Три больших круга, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым. Помимо трёх признаков равенства плоских треугольников, для сферических треугольников имеет место ещё один: два сферических треугольника равны, если их соответствующие углы равны.

Геометрия Римана

Двумерная геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения.

Если геометрия Евклида реализуется в пространстве с нулевой гауссовой кривизной, Лобачевского — с отрицательной, то геометрия Римана реализуется в пространстве с постоянной положительной кривизной..

Спасибо за внимание