Электронное приложение по подготовке к ОГЭ (модуль "геометрия, 2 часть,№26")

Данное приложение направлено на подготовку и успешное решение задач по геометрии 2 части, задачи №26.

Желаю удачи!!!

Задача№1

Задача№2

Задача№3

Задача№4

Задача№5

Каждая задача содержит комплект аналогичных текстов заданий и необходимой теории для их выполнения

Необходимая теория

Решаем сами

Решаем вместе

Трапеция  – четырехугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны  трапеции  называются основаниями, а непараллельные — боковыми сторонами

Трапеция называется  равнобедренной  ( равнобокой ), если ее боковые стороны равны.

Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.

Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:

В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 200, а площадь равна 1500, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 80, а площадь равна 320, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

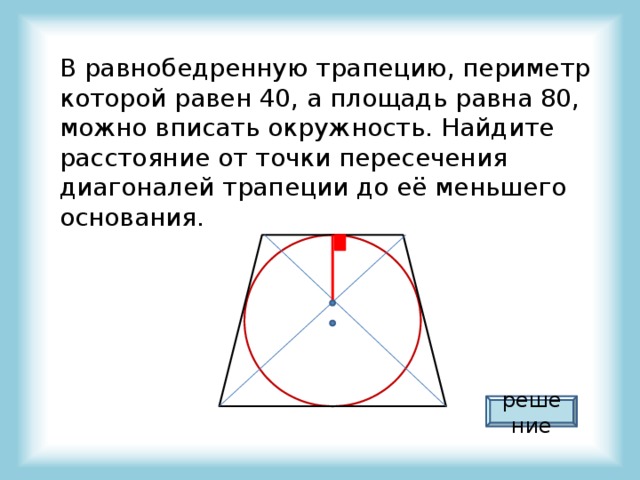
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

решение

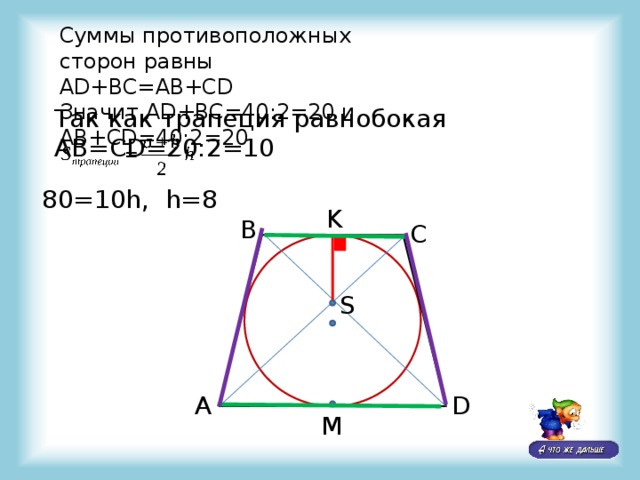
Суммы противоположных сторон равны

AD+BC=AB+CD

Значит AD+BC=40:2=20 и AB+CD=40:2=20

Так как трапеция равнобокая AB=CD=20:2=10

80=10h, h=8

K

B

C

S

D

A

M

K

B

C

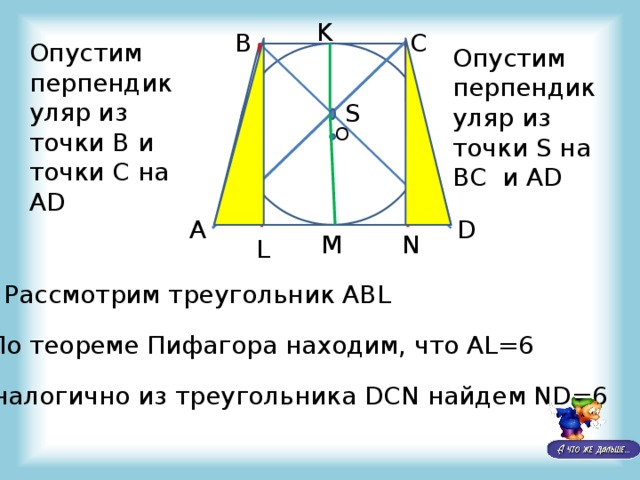
Опустим перпендикуляр из точки В и точки С на AD

Опустим перпендикуляр из точки S на BC и AD

S

O

D

A

N

M

L

Рассмотрим треугольник ABL

По теореме Пифагора находим, что AL=6

Аналогично из треугольника DCN найдем ND=6

K

C

B

S

8

10

10

8

O

A

D

M

6

6

N

L

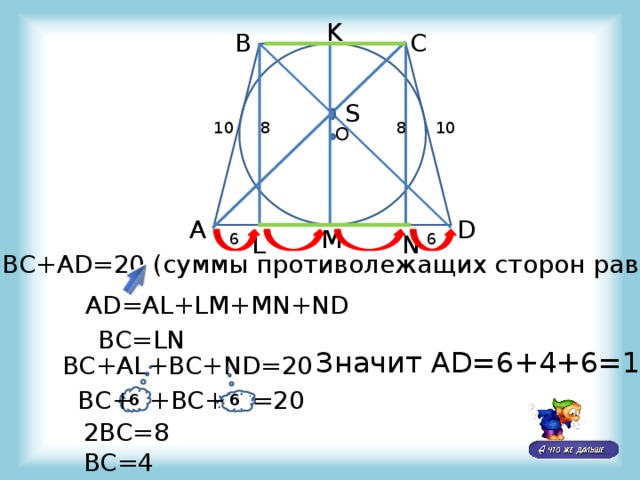
BC+AD=20 (суммы противолежащих сторон равны)

AD=AL+LM+MN+ND

BC=LN

Значит AD=6+4+6=16

BC+AL+BC+ND=20

BC+

+BC+

=20

6

6

2BC=8

BC=4

K

B

C

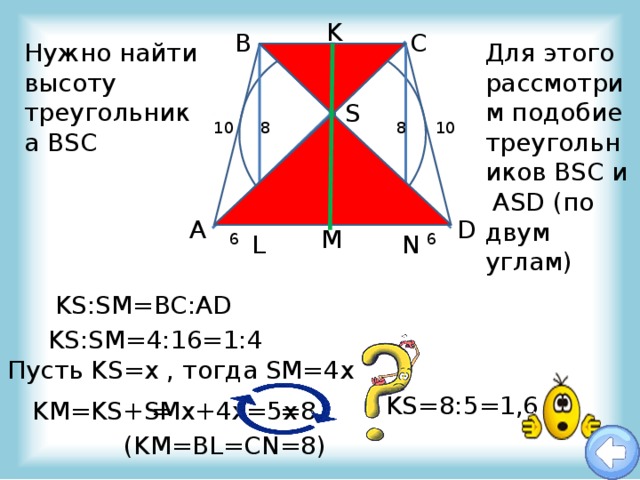
Для этого рассмотрим подобие треугольников BSC и ASD (по двум углам)

Нужно найти высоту треугольника BSC

S

8

8

10

10

O

D

A

M

6

N

L

6

KS:SM=BC:AD

KS:SM=4:16=1:4

Пусть KS=х , тогда SM=4х

KS=8:5=1,6

= х+4х=5х

=8

KM=KS+SM

(KM=BL=CN=8)

Необходимая

теория

Решаем сами

Решаем вместе

Описанная окружность около многоугольника  – это окружность, содержащая все вершины многоугольника.

Биссектриса угла — это луч, которых выходит из вершины угла, проходит между его сторонами и делит этот угол на два равных угла.

Вписанные углы, опирающиеся на одну хорду, равны.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=22.

В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.

В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=72, SQ=1.

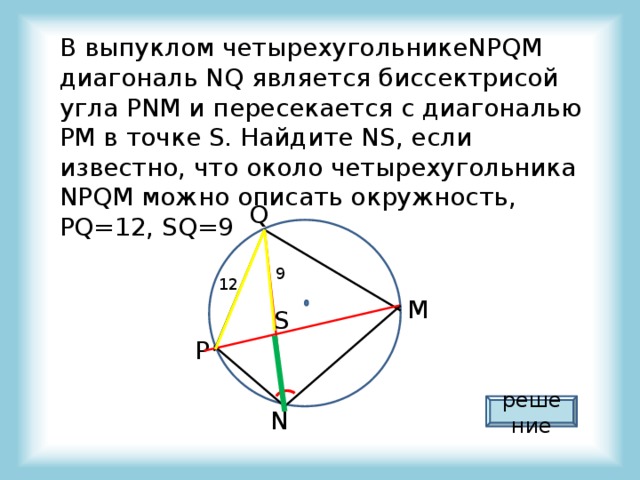
В выпуклом четырехугольникеNPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырехугольника NPQM можно описать окружность, PQ=12, SQ=9

Q

9

12

M

S

P

решение

N

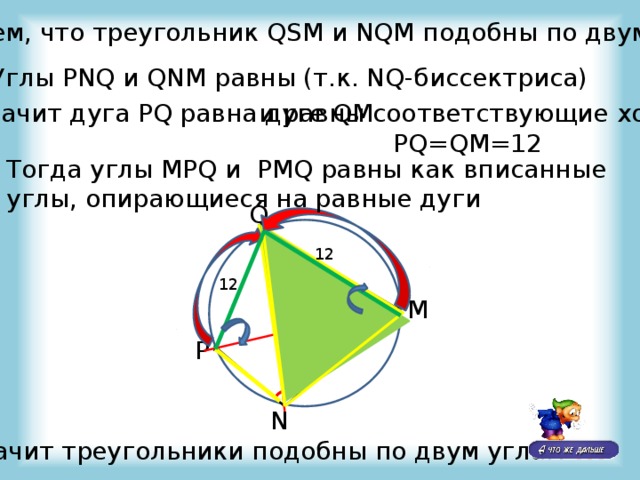
Докажем, что треугольник QSM и NQM подобны по двум углам

Углы PNQ и QNM равны (т.к. NQ-биссектриса)

Значит дуга PQ равна дуге QM

и равны соответствующие хорды

PQ=QM=12

Тогда углы MPQ и PMQ равны как вписанные углы, опирающиеся на равные дуги

Q

12

9

12

M

S

P

N

Значит треугольники подобны по двум углам !!!

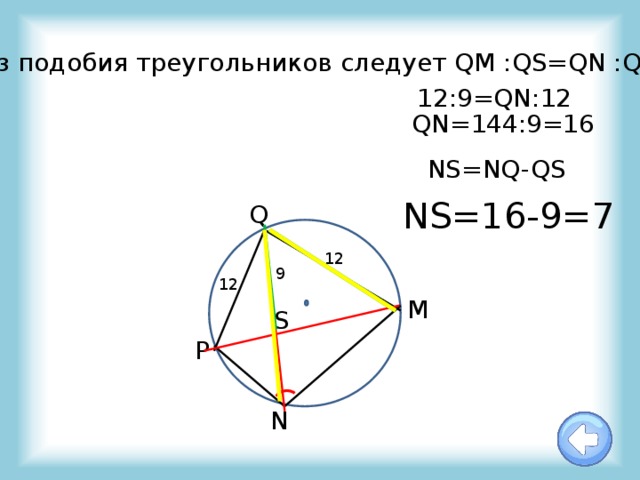
Из подобия треугольников следует QM :QS=QN :QM

12:9=QN:12

QN=144:9=16

NS=NQ-QS

NS=16-9=7

Q

12

9

12

M

S

P

N

Необходимая

теория

Решаем сами

Решаем вместе

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=7.

Трапеция называется  прямоугольной , если один из ее углов прямой

Прямая, имеющая одну общую точку с  окружностью  и лежащая с ней в одной плоскости, называется  касательной   к окружности

Квадрат касательной равен произведению секущей на её внешнюю часть.

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=4, BC=3.

4

A

D

E

K

С

B

3

решение

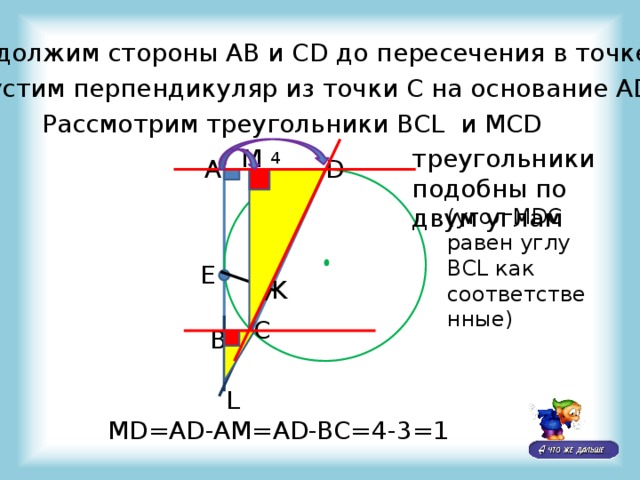
Продолжим стороны AB и CD до пересечения в точке L

Опустим перпендикуляр из точки С на основание АD

Рассмотрим треугольники BCL и MCD

треугольники подобны по двум углам

M

4

A

D

(угол MDC равен углу BCL как соответственные)

E

K

С

B

3

L

MD=AD-AM=AD-BC=4-3=1

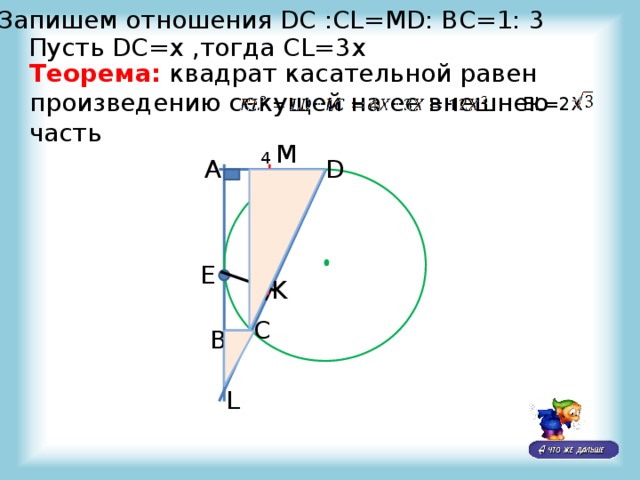
Запишем отношения DC :CL=MD: BC=1: 3

Пусть DC=x ,тогда CL=3х

Теорема: квадрат касательной равен произведению секущей на ее внешнею часть

EL=2X

M

4

A

D

E

K

С

B

3

L

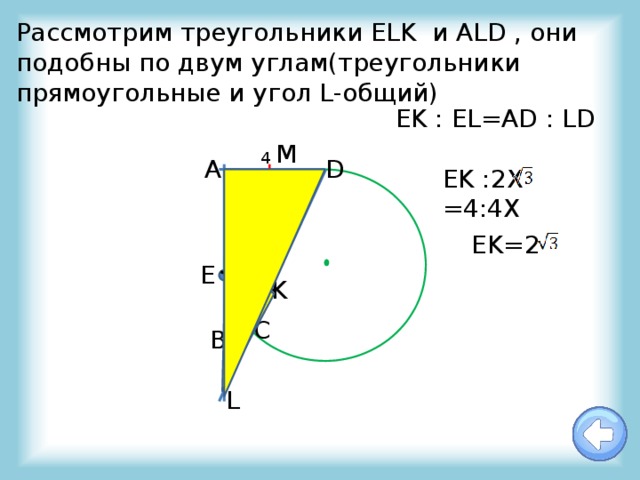
Рассмотрим треугольники ELK и ALD , они подобны по двум углам(треугольники прямоугольные и угол L-общий)

EK : EL=AD : LD

M

4

D

A

EK :2X =4:4Х

EK=2

E

K

С

B

3

L

Необходимая

теория

Решаем сами

Решаем вместе

Отрезки касательных к окружности, проведенные из одной точки, равны 

Сумма острых углов прямоугольного треугольника равна 90º.

Радиусы одной окружности всегда равны

Отрезки касательных к окружности, проведенные из одной точки, равны  

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Площадь прямоугольника равна произведению его длины на ширину.

В параллелограмме  ABCD  проведена диагональ  AC . Точка  O  является центром окружности, вписанной в треугольник  ABC . Расстояния от точки  O  до точки  A  и прямых  AD  и  AC  соответственно равны 5, 4 и 3. Найдите площадь параллелограмма  ABCD .

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 6 и 5. Найдите площадь параллелограмма ABCD.

В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 7 и 5. Найдите площадь параллелограмма ABCD.

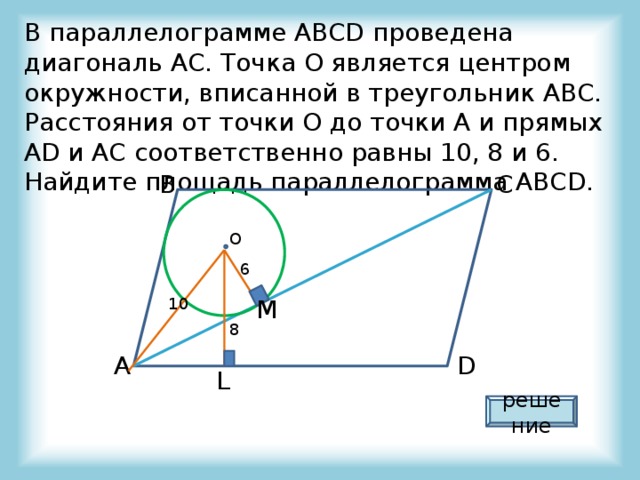
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 8 и 6. Найдите площадь параллелограмма ABCD.

C

B

O

6

M

10

8

A

D

L

решение

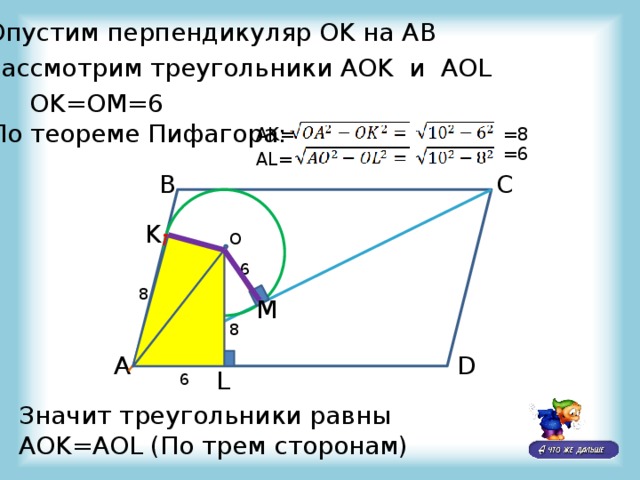
Опустим перпендикуляр OK на АВ

Рассмотрим треугольники AOK и AOL

OK=OM=6

По теореме Пифагора:

=8

AK=

=6

AL=

C

B

K

O

6

8

M

10

8

A

D

L

6

Значит треугольники равны AOK=AOL (По трем сторонам)

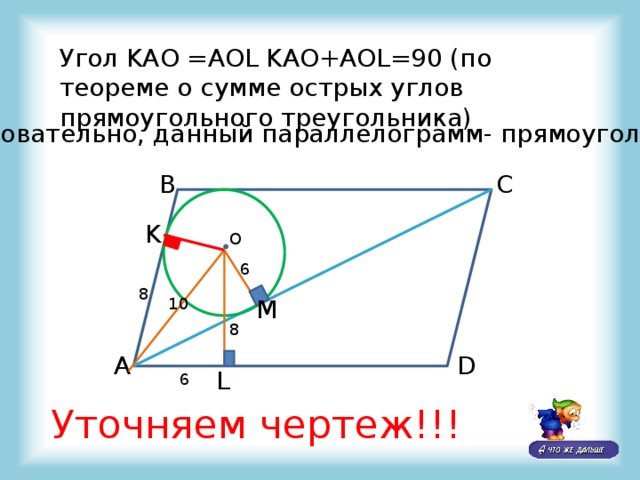
Угол KAO =AOL KAO+AOL=90 (по теореме о сумме острых углов прямоугольного треугольника)

Следовательно, данный параллелограмм- прямоугольник

C

B

K

O

6

8

M

10

8

D

A

L

6

Уточняем чертеж!!!

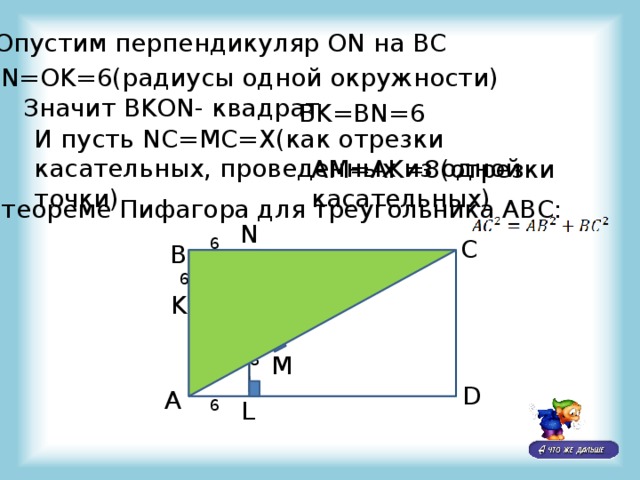
Опустим перпендикуляр ON на BC

ON=OK=6(радиусы одной окружности)

Значит BKON- квадрат

BK=BN=6

И пусть NC=MC=X(как отрезки касательных, проведенных из одной точки)

AM=AK=8(отрезки касательных)

По теореме Пифагора для треугольника ABC:

N

6

C

B

6

K

6

6

10

8

M

D

A

6

L

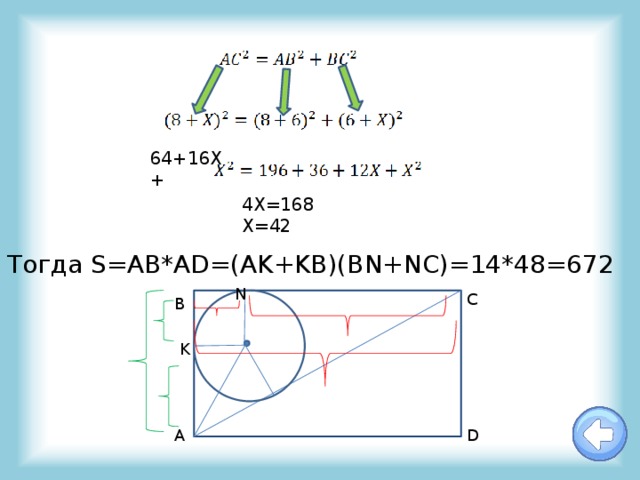
64+16X+

4X=168

X=42

Тогда S=AB*AD=(AK+KB)(BN+NC)=14*48=672

N

C

B

K

D

A

Необходимая

теория

Решаем сами

Решаем вместе

Площадь трапеции равна произведению полусуммы ее оснований на высоту

Средняя линия трапеции -отрезок, соединяющий середины боковых сторон этой трапеции.

Средняя линия трапеции равна полусумме оснований этой трапеции

Внутренние накрест лежащие углы это два угла во внутренней области параллельных прямых и на разных сторонах секущей

Накрест лежащие углы попарно равны.

Биссектриса угла - это луч с началом в вершине угла, делящий угол на две равные части.

Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 26, а основание BC равно 8. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Боковые стороны AB и CD трапеции ABCD равны соответственно 36 и 39, а основание BC равно 12. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 30, а основание BC равно 6. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

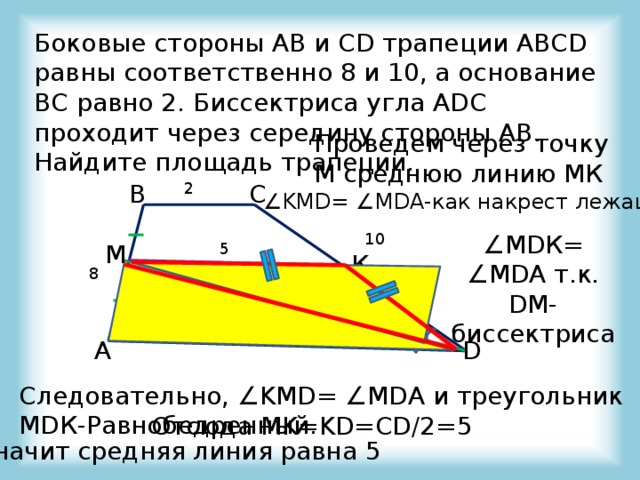
Боковые стороны AB и CD трапеции ABCD равны соответственно 8 и 10, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

Проведем через точку М среднюю линию МК

C

2

B

∠ KMD= ∠MDA-как накрест лежащие

∠ MDК= ∠MDA т.к. DМ-биссектриса

10

M

5

К

8

D

A

Следовательно, ∠KMD= ∠MDA и треугольник MDК-Равнобедренный.

Отсюда MK=KD=CD/2=5

Значит средняя линия равна 5

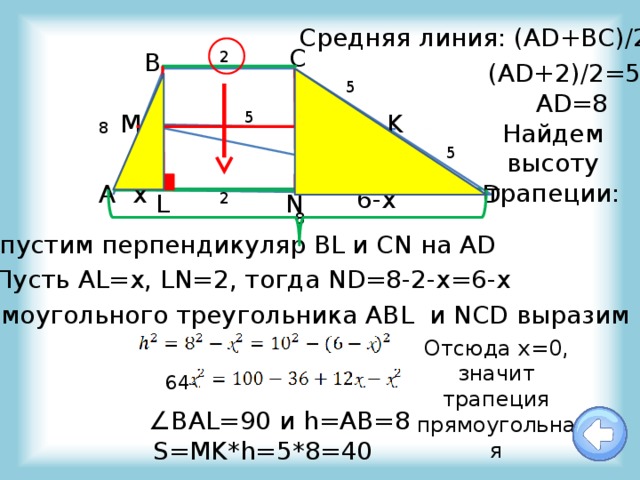
Cредняя линия: (AD+BC)/2=5

С

2

В

(AD+2)/2=5

5

AD=8

5

K

M

Найдем высоту трапеции:

8

5

А

x

D

6-x

L

2

N

8

Опустим перпендикуляр BL и CN на AD

Пусть AL=x, LN=2, тогда ND=8-2-x=6-x

Из прямоугольного треугольника ABL и NCD выразим высоту:

Отсюда х=0, значит трапеция прямоугольная

64-

∠ BAL=90 и h=AB=8

S=MK*h=5*8=40

Необходимая

теория

Решаем сами

Решаем вместе

Если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный

Биссектриса треугольника делит третью сторону на отрезки, пропорциональные двум другим сторонам

длины прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону



BC=a, AC=b, AB=c,

сторона AC - наибольшая

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 60. Найдите стороны треугольника ABC.

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 72. Найдите стороны треугольника ABC.

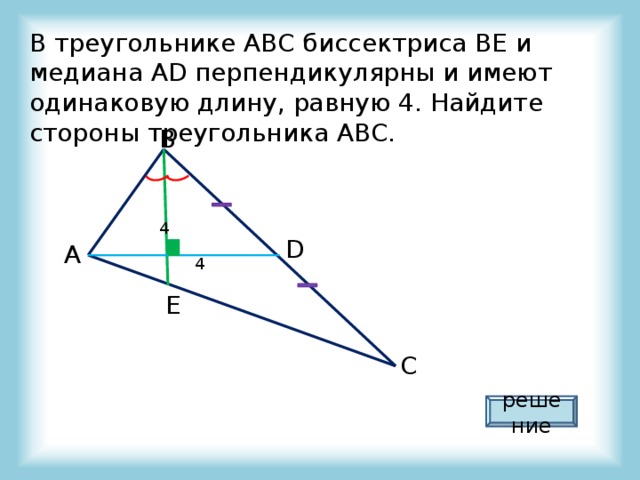
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 4. Найдите стороны треугольника ABC.

В

4

D

А

4

Е

С

решение

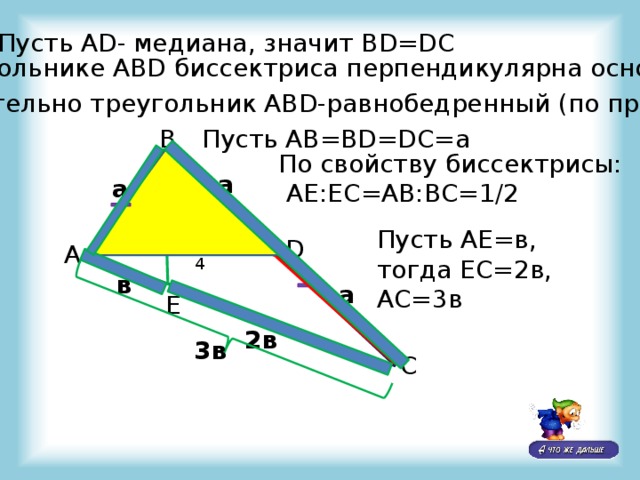
Пусть АD- медиана, значит ВD=DС

В треугольнике АВD биссектриса перпендикулярна основанию

Следовательно треугольник АВD-равнобедренный (по признаку)

В

Пусть АВ=ВD=DC=а

По свойству биссектрисы:

АЕ:ЕС=АВ:ВС=1/2

а

а

4

Пусть АЕ=в, тогда ЕС=2в, АС=3в

D

А

4

в

а

Е

2в

3в

С

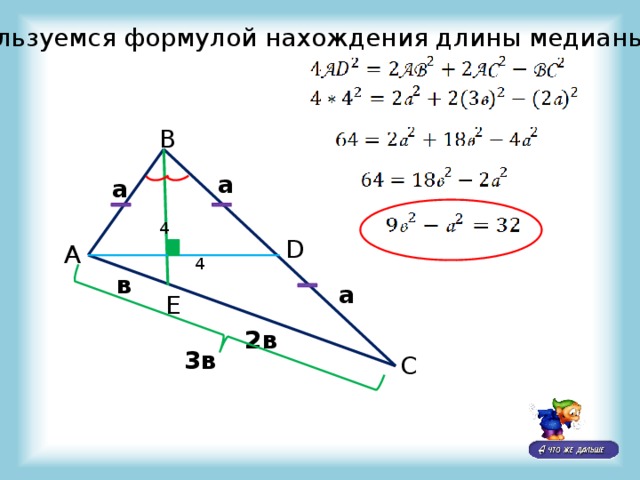
Воспользуемся формулой нахождения длины медианы:

В

а

а

4

D

А

4

в

а

Е

2в

3в

С

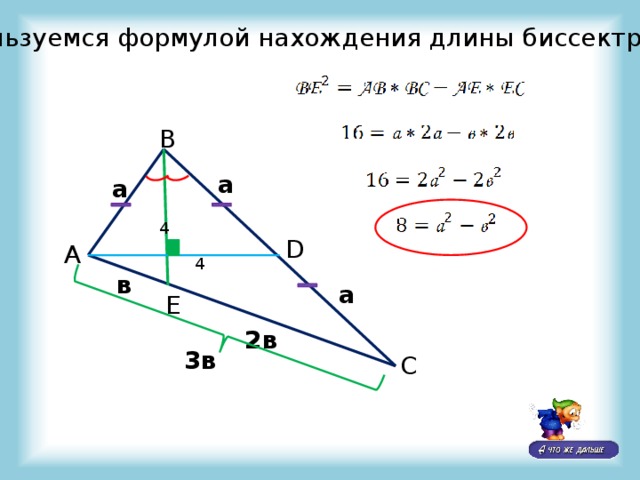
Воспользуемся формулой нахождения длины биссектрисы:

В

а

а

4

D

А

4

в

а

Е

2в

3в

С

Получим систему:

Выполнив сложение уравнений получим:

Отсюда

Тогда

Конец!!!