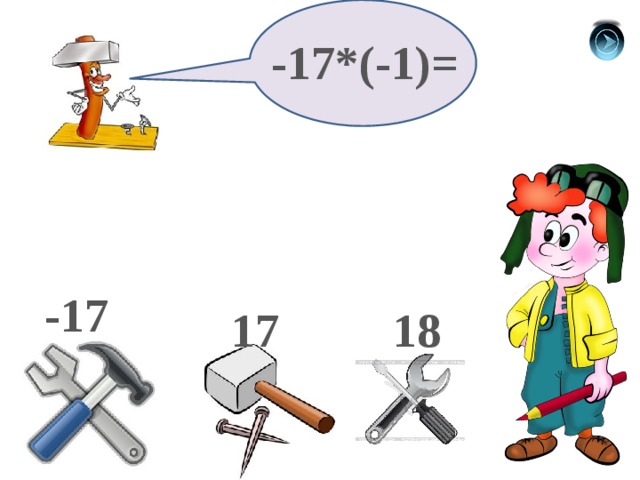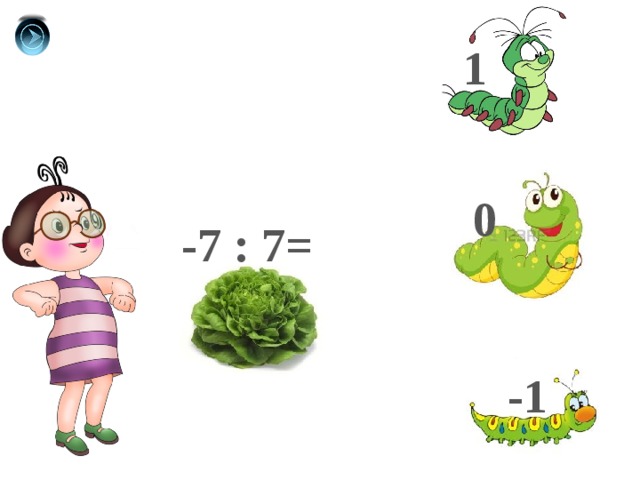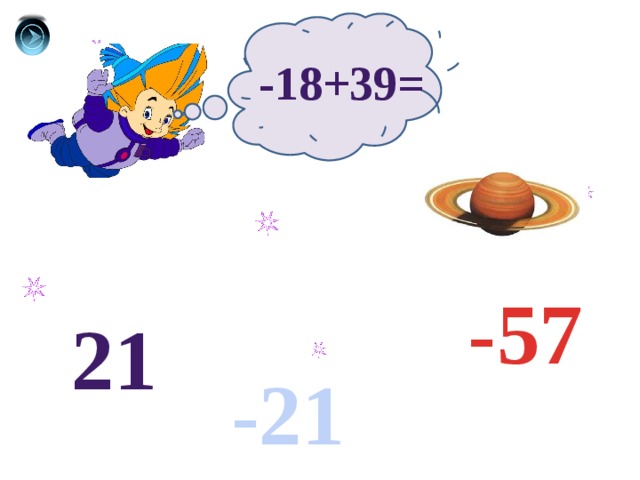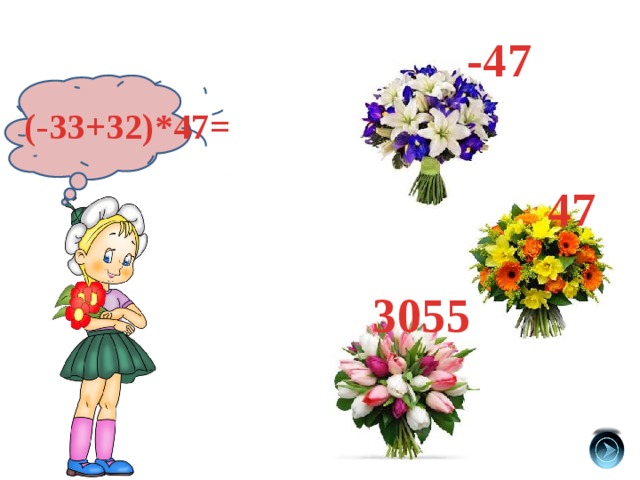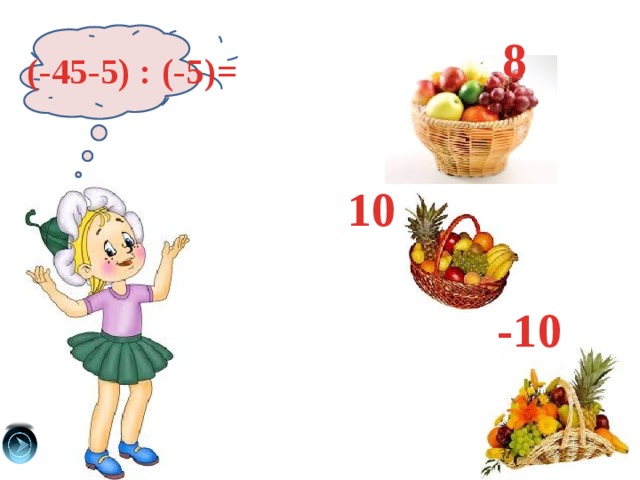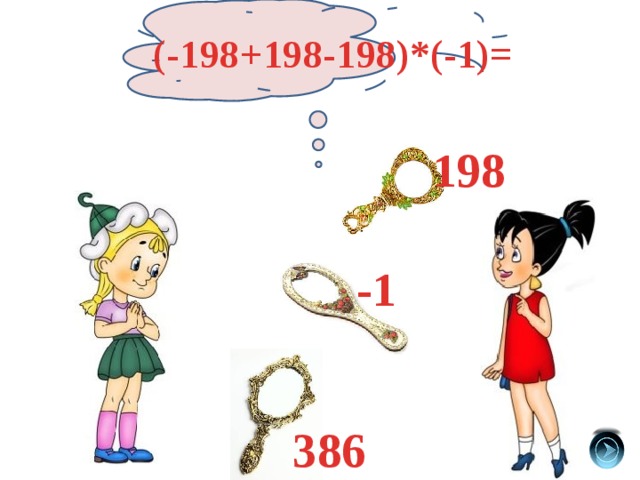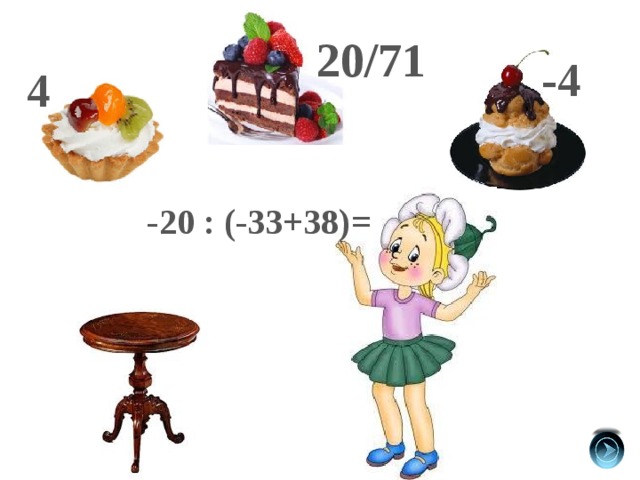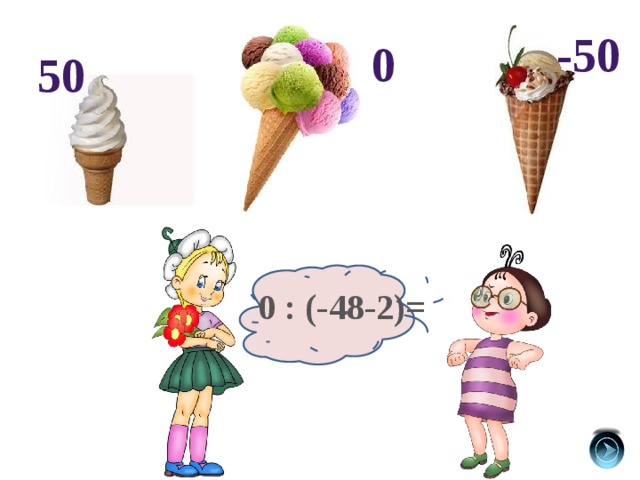Арифметические действия
с отрицательными числами

Связь с другими предметами
Устный счет
Практика
Вопросы по теории
Множества чисел
Игры, ребусы, загадки…
Правила, опорные схемы
Тренажеры

1. Восстанови цепочку
2. найди правильный ответ
3. Целебные цветы
4. Заполни пропуски
5. Вставьте пропущенное число
6. Вычисли быстро
7. посчитаем
8. Заполни полосу числами
9. Потерянные знаки
10. Сколько будет?
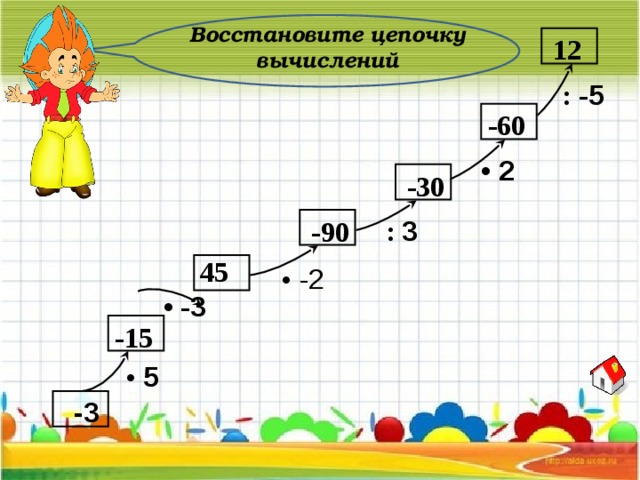
Восстановите цепочку вычислений
12
: - 5
-60
• 2
-30
-90
: 3
45
• - 2
• - 3
-15
• 5
-3

- 9 + (-3) =
Найдите правильный
ответ.
6
-12
12
-6

- 18,5 + (-23,8) =
Найдите правильный
ответ.
-5,3
-41,13
-42,3
42,3
5,3

- 16,4 + (-0,08) =
Найдите правильный
ответ.
-16,48
17,48
16,48
-16,32
-17,2

- 26,33 + (-25,97) =
Найдите правильный
ответ.
0,36
52,3
-0,36
-51,03
-52,3

Помогите мне собрать целебные цветы на этой цветочной поляне
Если произведение чисел на лепестках совпадает с числом на листке, то цветок целебный

-0,5
4
-10
целебный
20

-0,5
-4
-10
ядовитый
20

-5
4
-25
целебный
500

-0,5
-20
40
ядовитый
-400

-5
-4
30
целебный
600

-50
-20
-4
ядовитый
400

Вставьте нужное число так, чтобы получилось верное равенство
-60+____ =100
50 - ____ =100
____ -(-20) =100
____ +(-100)=100
-20+____=-100
-30-____ =-100
40 - ____ =-100
____-(-60)=-100
160
(-80)
(-50)
70
80
140
200
-160

Вставь число, чтобы получилось верное равенство:
14
-( … )=-14
-( … )=21
-( … )=98
-( … )=-34
-(-(+3))= …
-(-(-8))= …
-(-(-(-9)))= …
-21
-98
34
3
-8
9

2*(-3)

4-7

-8*5

-10+5

-8*0

5-(-3)

0*(-7)

3-10

7:(-1)

8:0

5*(-1)

-5+11

-6-3

1*(-7)

-4+(-5)

3+(-6)

-6*(-3)

2-10
-8
-20
4*(-5)
-6
-2*3
6-(-4)
10
0
-5*0
-3
-8+5
-8
8:(-1)
-5
-9
-9:(-1)
1*(-5)
-14
-9+(-5)
-2*(-0,1)
0,2

Заполните полосу числами, записывая в каждой новой клетке результат умножения предыдущих чисел.
0,4
-0,2
10
-2
-0,8
-0,32
0,08
-0,1
2
-0,2
-0,4

Помогите в равенствах расставить потерянные знаки
_
6*(-2)= 12
3-13= 10
9+7=-2
4-9=-13
-5:1= 5
5*(-10)=50
_
_
_
_
_

0
50
-100
50
+
-50
100:(-1)
-25*(-2)

1. лестница
2. Узнай Радиус ядра Луны
3. Вычеркни буквы
4. Созвездие Тельца
5. Задачи
6. Разгадай слово
7. Денежные операции
8. Составь равенство
9. солнышко
10. Реши пример
11.Заполни таблицу
12.Умножаем дроби
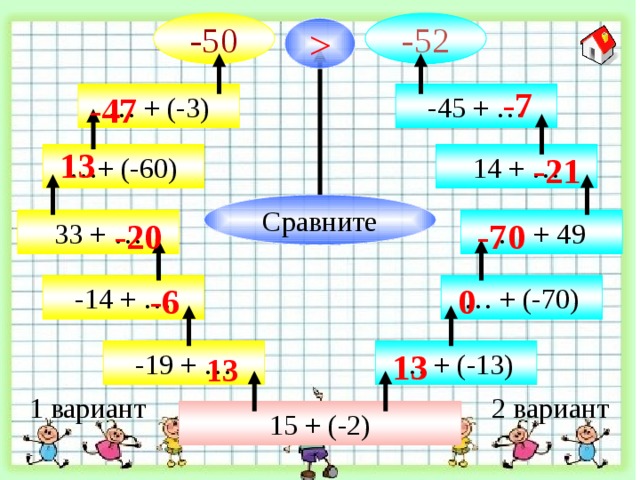 -7 -47 … + (-3) -45 + … 13 … + (-60) 14 + … -21 Сравните -20 -70 33 + … … + 49 -6 0 … + (-70) -14 + … -19 + … 13 … + (-13) 13 2 вариант 1 вариант 15 + (-2) " width="640"
-7 -47 … + (-3) -45 + … 13 … + (-60) 14 + … -21 Сравните -20 -70 33 + … … + 49 -6 0 … + (-70) -14 + … -19 + … 13 … + (-13) 13 2 вариант 1 вариант 15 + (-2) " width="640"
-50
-52
-7
-47
… + (-3)
-45 + …
13
… + (-60)
14 + …
-21
Сравните
-20
-70
33 + …
… + 49
-6
0
… + (-70)
-14 + …
-19 + …
13
… + (-13)
13
2 вариант
1 вариант
15 + (-2)

Ответ в позволит узнать
радиус внутреннего ядра Луны,в км
7,5
+(-12,75)=
-5,25
-15,5
-3,1
: 5=
350
-3,1
+353,1=
-15,5
-10,25=
-5,25
-5*(-3)*0,5=
7,5

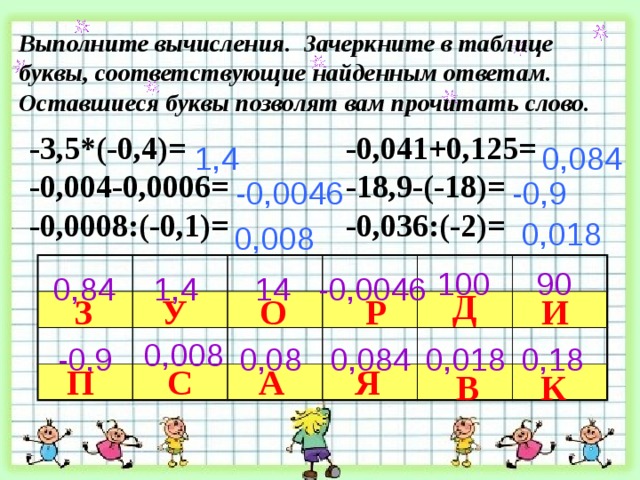
Выполните вычисления. Зачеркните в таблице буквы, соответствующие найденным ответам. Оставшиеся буквы позволят вам прочитать слово.
-0,041+0,125=
-3,5*(-0,4)=
-0,004-0,0006=
-18,9-(-18)=
-0,036:(-2)=
-0,0008:(-0,1)=
1,4
0,084
-0,0046
-0,9
0,018
0,008
100
90
1,4
-0,0046
0,84
14
Д
З
И
Р
О
У
0,008
0,18
0,018
0,084
0,08
-0,9
П
С
А
Я
В
К

ЗОДИАК - пояс неба, по которому Солнце совершает своё видимое годовое движение через 12 созвездий.
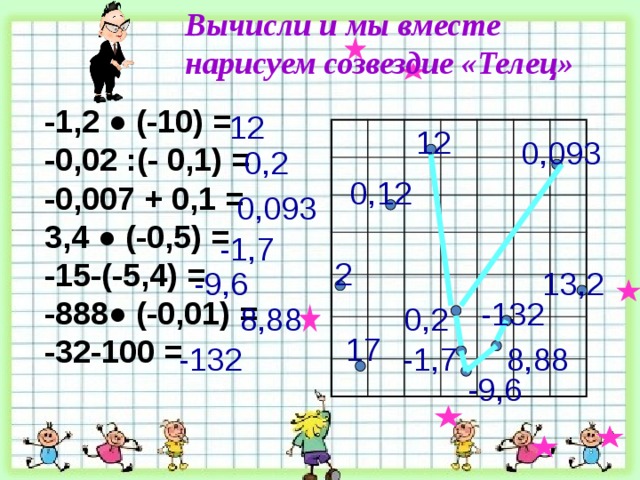
Вычисли и мы вместе
нарисуем созвездие «Телец»
-1,2 ● (-10) = -0,02 :(- 0,1) = -0,007 + 0,1 = 3,4 ● (-0,5) = -15-(-5,4) = -888● (-0,01) = -32-100 =
12
12
0,093
0,2
0,12
0,093
-1,7
2
13,2
-9,6
-132
0,2
8,88
17
-132
-1,7
8,88
-9,6


Птица клест-еловик несет яйца и высиживает птенцов зимой.
Даже при температуре воздуха -35 0 в гнезде температура не ниже 14 0 .
На сколько температура в гнезде выше температуры воздуха?
ответ
49


Шмели выдерживают температуру до -7,8 0 , пчелы – выше этой на 1,4 0 .
Какую температуру выдерживают пчелы?
ответ
-6,4


Во время пребывания космонавта в открытом космосе солнечная сторона его скафандра находилась при температуре
+ 140 0 , а теневая – при температуре – 130 0 . Определите разность температур между солнечной и теневой сторон скафандра космонавта.
270
ответ


Бережливый хозяин должен хорошо знать как размер своего имущества, так и свои долги. И вот однажды ростовщик решил посчитать, с прибылью для себя или с убытком он прожил этот месяц? Если:
- Первый человек отдал ему 32,4 лиры своего долга;
- Второму он дал в долг 50% этих денег;
- На строительство башни он пожертвовал 30,8;
- Третий вернул 17,6 лиры;
- И последняя сделка принесла ему доход 10 лир.

Решение задачи
- Хозяину вернули долг 32,4 лиры, значит он в плюсе.
- От имеющейся суммы половину хозяин занял , т.е.
32,4 - 32,4 0,5 .
3) От оставшейся суммы хозяин пожертвовал 30,8 лиры, т.е.
32,4 - 32,4 0,5-30,8 .
4) Хозяину вернули долг 17,6 лиры, т.е.
32,4 - 32,4 0,5-30,8+17,6 .
5) Последняя сделка принесла 10 лир, т.е.
32,4 - 32,4 0,5-30,8+17,6+10 .
6) В итоге получаем:
32,4 – 32,4 ∙ 0,5 – 30,8 + 17,6 + 10 = 13

Разгадайте слово
А
У
П
Г
Т
М
Р
-8
Б
40
А
-30
У
8
П
1
Г
4
А
-3
0
Т
А
-6
Х
-2
-7
Х
Р
Б
А
А
М
-2
0
-3
-8
8
4 0
4
-6
-7
-30
1
-10+(-20)= 18+(-18)=
-26+66 = -8-(-5)=
27+(-19)= -3+10-6=
-1,3-5,7 = 2-(-2)=
17,4-25,4= -6-0=
-0,25-1,75=

Складывать и вычитать отрицательные числа научились древнекитайские ученые ещё до нашей эры.
Индийские математики представляли себе положительные числа как «имущество», а отрицательные числа как «долги».
Индийский математик Брахмаг ýпта (VII в.) излагал правила сложения и вычитания так:
«Сумма двух имуществ есть имущество»
«Сумма двух долгов есть долг»
«Сумма имущества и долга равна их разности»

Подсчитайте итоги денежных операций и запишите результат с помощью положительных и отрицательных чисел:
а)доход 5 тыс.руб и расход 9 тыс.руб
б)расход12 тыс.руб и доход 3 тыс.руб
в) доход 6 тыс.руб и расход 2 тыс.руб
г)расход8 тыс.руб и расход10 тыс.руб
д) доход 7 тыс.руб и расход 7 тыс.руб

= -4
-9
+5
= -9
+3
-12
=4
+6
-2
-8
-10
= -18
= 0
-7
+7

Поиграем …
-1; -2; -3; -4; -5; -6; -7; -8; -9; -10
Даны числа:
Используя каждое число
по одному разу, составьте три верных
Равенства.
-1 + (-4) = -5
-2 + (-6) = -8
-3 + (-7) = -10
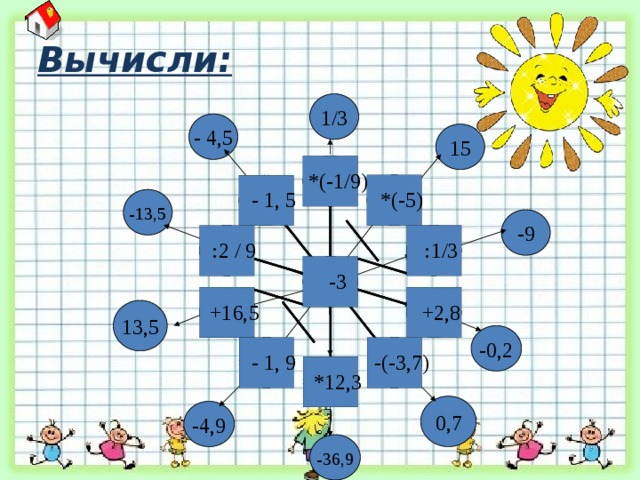
Вычисли:
1/3
- 4,5
15
-13,5
-9
13,5
-0,2
0,7
-4,9
-36,9

Складывать и вычитать отрицательные числа научились древнекитайские учёные ещё до нашей эры.
Индийские математики представляли себе положительные числа как «имущества», а отрицательные как «долги».
Вот как индийский математик VII в. излагал правило сложения: «Сумма двух имуществ есть имущество»
Решив пример, вы узнаете , как звали этого математика.
- 2,3 * 0,1 + 35 *(- 0,01)-(-2,1) * (-0,2) + (4,8- 4,38 + 2,1- 2,7- 0,51)*(-2)
1
2
6
10
11
9
8
7
5
4
3
Г
2,52
Р
-0,35
У
Т
-0,18
1,42
А
0,42
Б
-0,23
П
-0,71
Х
М
-0,58
-1
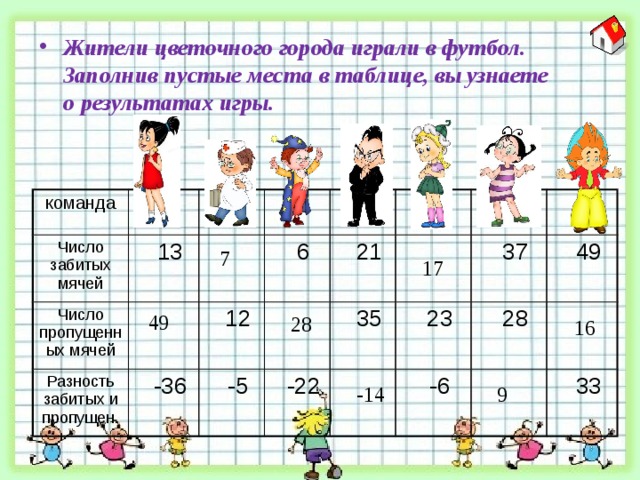
- Жители цветочного города играли в футбол. Заполнив пустые места в таблице, вы узнаете о результатах игры.
команда
Число забитых мячей
13
Число пропущенных мячей
Разность забитых и пропущен.
-36
6
12
-5
21
-22
35
23
37
-6
49
28
33
7
17
49
28
16
9
-14

Вычисли
-85
1/3
-1/3
-0,06
1/4
-27

География
Биология
Физика
История
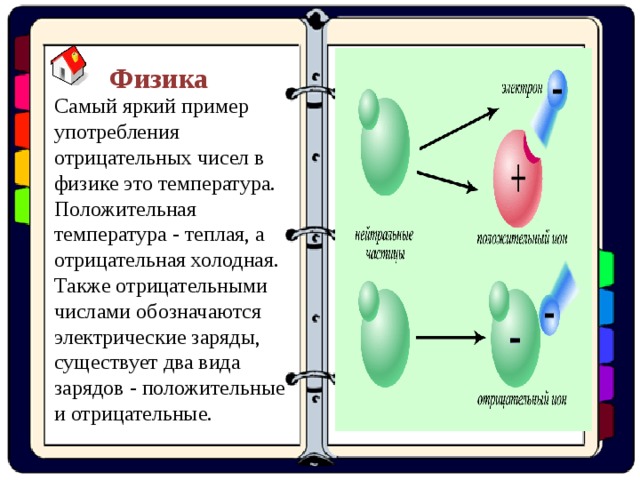
Физика
Самый яркий пример употребления отрицательных чисел в физике это температура. Положительная температура - теплая, а отрицательная холодная. Также отрицательными числами обозначаются электрические заряды, существует два вида зарядов - положительные и отрицательные.

География
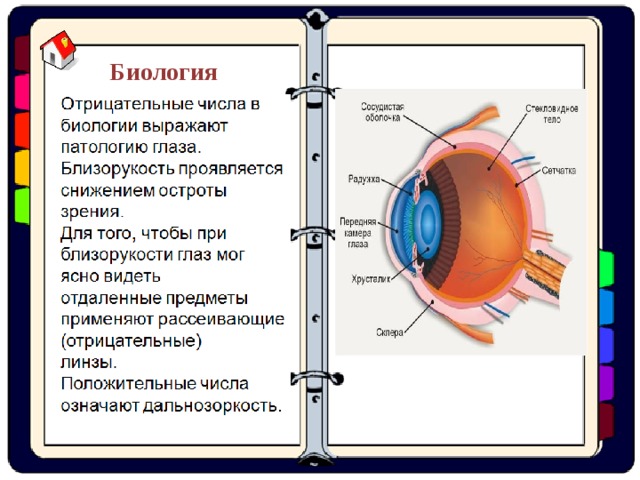
Биологияя
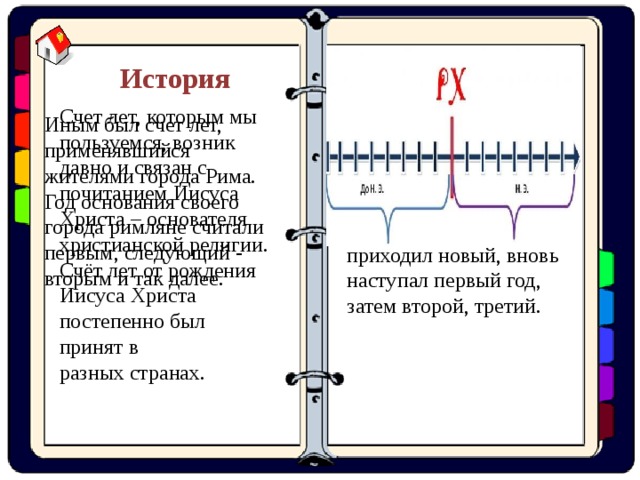
В Древнем Египте каждый раз, когда начинал править новый царь, счёт лет начинался заново. Когда этот царь умирал и к власти приходил новый, вновь наступал первый год, затем второй, третий.
История
Счет лет, которым мы пользуемся, возник давно и связан с почитанием Иисуса Христа – основателя христианской религии. Счёт лет от рождения Иисуса Христа постепенно был принят в
разных странах.
Иным был счет лет,
применявшийся
жителями города Рима.
Год основания своего города римляне считали
первым, следующий - вторым и так далее.

???!!!!!
Отрицательные числа -
жизненная необходимость !

1. Математический диктант
2. Сформулируй правило
3. блиц-опрос
4. кроссворд
5. кросс-опрос
6. блиц-викторина
7. Исправь ошибки
8. Что не так?
9. Выбери верную запись
10. загадки

Математический диктант
1. Сумма двух чисел с разными знаками всегда положительна.
2. Сумма двух чисел с разными знаками всегда отрицательна.
3. Сумма двух чисел с разными знаками может быть равной 0.
4. Сумма двух чисел с разными знаками, но с одинаковыми модулями равна 0.
5 . Изменить величину – это значит увеличить ее.
6. Прибавить к числу а число b – значит изменить число а на b единиц.
7. Модуль суммы равен сумме модулей.
8. Если складываются отрицательные числа, то их сумма отрицательна.
проверка

^^--^ - ^-

Сформулируйте правило
нулю
1 .Сумма двух противоположных чисел равна ______.
2. Чтобы сложить два отрицательных числа, надо:
1)________________,
2)________________________________ .
3 .Чтобы сложить два числа с разными знаками, надо:
1)_______________________________________ ,
2)________________________________________
_________________________________ .
4 .Чтобы из данного числа вычесть другое, надо ______________________________________ _________________________________ .
5 .Чтобы найти длину отрезка на координатной прямой, надо из ______________________
___________________________________.
сложить их модули
поставить перед результатом знак «-»
из большего модуля слагаемых вычесть меньший
поставить перед полученным числом знак того слагаемого, модуль которого больше
к уменьшаемому прибавить число противоположное вычитаемому: a - b = a +(- b )
координаты его правого
конца вычесть координату его левого конца
 у, х 0, у 0. " width="640"
у, х 0, у 0. " width="640"
Блиц – опрос
1.Сумма противоположных чисел равна…
Ответ: 0
2. Какое из чисел больше: отрицательное или 0?
Ответ: 0
3. Если перемножить 5 положительных и 8 отрицательных чисел, то с каким знаком мы получим результат?
Ответ: «+»
4. При каких значениях x и y верно соотношение ?:
Ответ: при х у, х 0, у 0.
3
2
1
6
4
8
7
10
5
9
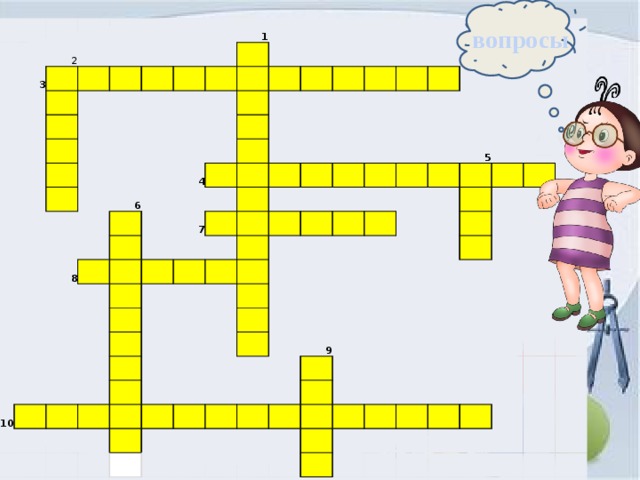
вопросы

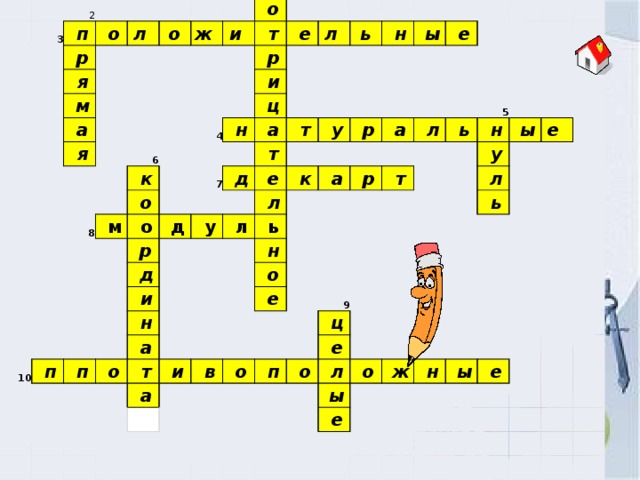
По вертикали:
- Какое число выражает уменьшение любой величины?
- Линия, на которой отмечают числа
- Число, которое не является ни положительным, ни отрицательным
- Число, показывающее положение точки на прямой
- Натуральные числа, противоположные им числа, нуль
По горизонтали:
3. Числа, расположенные на вертикальной прямой выше начала координат
4. Числа, которые используют при счете предметов
7. Французский математик, который ввел координатную прямую
- Расстояние(в ед.отрезках) от начала координат до точки на координатной прямой
10. Два числа, отличающиеся друг от друга только знаками
2
3
п
о
р
л
я
м
о
а
ж
1
я
о
и
т
р
е
6
к
8
и
л
4
м
ь
ц
о
н
н
о
а
7
р
ы
т
д
д
т
е
д
у
10
е
у
и
л
п
л
к
р
н
а
а
п
ь
а
р
н
о
л
5
ь
о
т
т
е
а
н
и
ы
в
у
9
л
о
е
ц
ь
п
е
о
л
ы
о
ж
е
н
ы
е


Блиц-викторина
1. Может ли сумма двух отрицательных чисел быть числом натуральным?
2. Можно ли утверждать, что разность двух натуральных чисел является натуральным числом?
3. Может ли разность двух отрицательных чисел быть целым положительным числом?
4. Может ли произведение двух отрицательных чисел быть числом отрицательным?
5. Может ли разность двух целых чисел быть равной одному из них?
6. Может ли сумма двух целых положительных чисел быть равной 0?
7. Может ли произведение двух целых положительных чисел быть равным 0?
8. Может ли произведение двух целых чисел быть равным 0?
9. Какой знак имеет произведение всех целых чисел от -20 до 20?
10. Может ли сумма двух отрицательных чисел быть больше их частного?

Найди и исправь ошибки
1.Сумма противоположных чисел равна
1
0
2.Чтобы сложить два отрицательных числа, надо сложить их модули
и перед результатом поставить знак «-»
3.Чтобы сложить два числа с разными знаками, надо
- из большего модуля слагаемых вычесть меньший
- поставить перед полученным числом знак того слагаемого, модуль которого
меньше
больше
-
4. a - b = a
+
(-b)
5. Если перемножить пять отрицательных чисел,
то ответ будет со знаком
«-»
«+»

Что не так???!!!
.
+
-
=
-
-
:
=
+
+
-
-
.
=
-
+
+
-
:
-
-
+
-
=

Выбирай верную запись!
Чтобы из данного числа вычесть другое, надо :
a-b=b-a
a-b=a-(-b)
a-b=a+(-b)

Чтобы сумму получить,
Нужно два числа …
Сложить!!!!

Если что-то забираем,
Числа, дети,…
Вычитаем!!!!

Если больше раз так в пять,
Числа будем...
Умножать!!!!

Если меньше, стало быть,
Числа будем мы...
Делить!!!!

По-латыни это слово «меньше» означает,
А у нас-то этот знак числа вычитает.
минус!!!!

1. Игры - ходилки
2. Игры с кубиком
3. загадки
4.ребусы
5. Загадка Незнайки
6. Расставь знаки
7. Передвинь цифру
8. задача-стих
9. Угадай следующее число
10. стишки
11. Творческое задание

Игра-ходилка 1
Игра-ходилка 2
правила

Правила игры:
В игре могут принимать участие от 2 до 4 человек. Игры выбирают себе фишки и ставят их на старт. Игроки по очереди бросают кубик и передвигают свою фишку на выпавшее на нем количество ходов. Остановившись на своем поле игрок должен сосчитать доставшийся ему пример. В случае ошибки игрок пропускает ход. Побеждает тот, кто первым доберется до финиша.
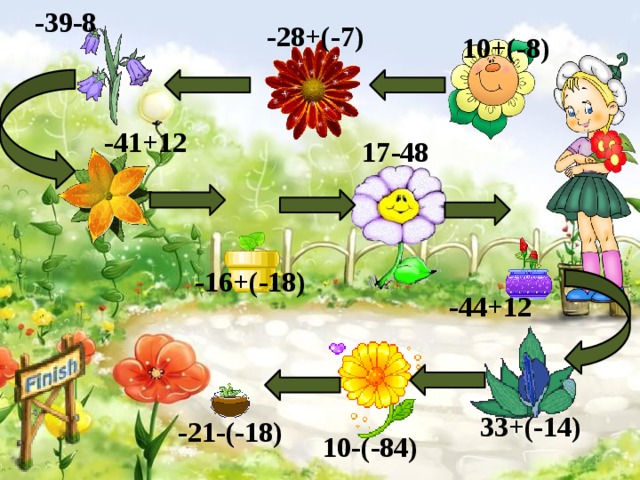
-39-8
-28+(-7)
10+(-8)
-41+12
17-48
-16+(-18)
-44+12
33+(-14)
-21-(-18)
10-(-84)

Победа!
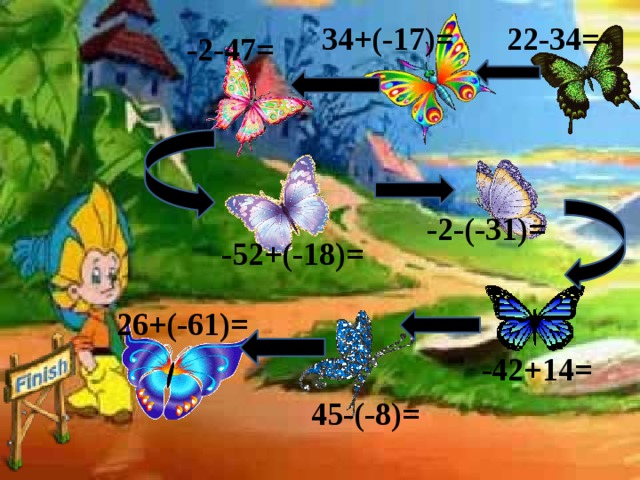
34+(-17)=
22-34=
-2-47=
-2-(-31)=
-52+(-18)=
26+(-61)=
-42+14=
45-(-8)=

Победа!

Игра 1
Игра 2
Игра 3

Для работы потребуются
- Играют несколько человек
- Играющие договариваются о количестве бросков
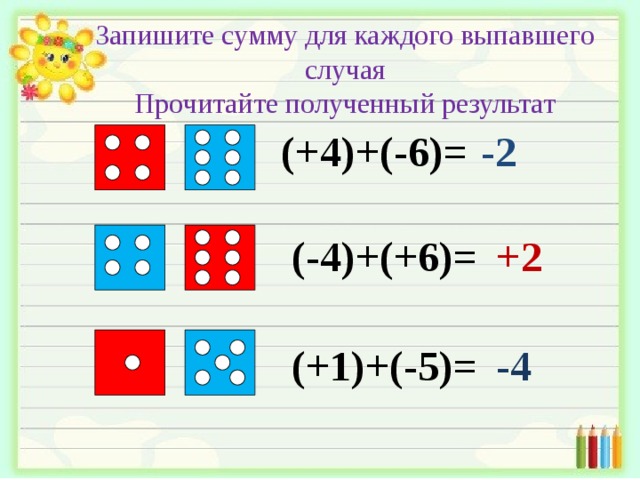
Запишите сумму для каждого выпавшего случая
Прочитайте полученный результат
-2
(+4)+(-6)=
(-4)+(+6)=
+2
(+1)+(-5)=
-4

Если выигрышных и проигрышных очков поровну, то получится нуль
Если выигрышных очков больше, то получится выигрыш
Если проигрышных очков больше, то получится проигрыш
Для работы потребуются
- Играют несколько человек
- Играющие договариваются о количестве бросков
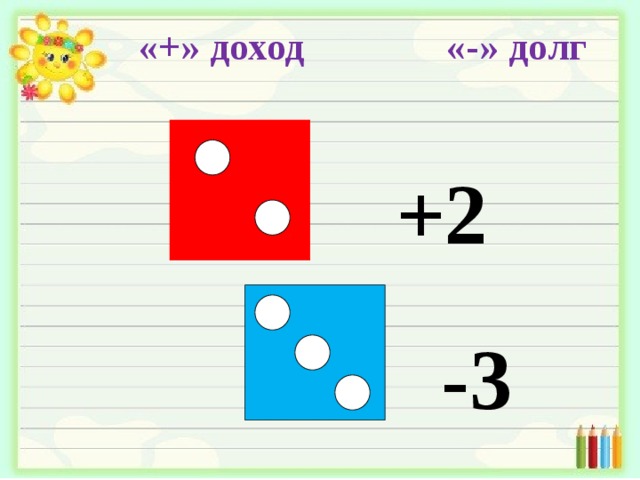
«+» доход «-» долг
+2
-3

-Необходимо найти сумму выпавших «доходов» и «долгов».
-Побеждает игрок получивший наибольший доход или (в случае только долгового результата)имеющий наименьший долг

- Играют несколько человек
- Играющие договариваются о количестве бросков
- Кто раньше окажется ближе к финишу, то победитель
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Математики урок.
Только прозвенел звонок,
Мы за партами, и вот
Начинаем устный...
счет

Ученик я хоть куда,
Не балую никогда,
Хоть я и не пионер,
Но ребятам всем...
пример

Выполнил в тетради я
Четко, словно ритм,
Друг за другом действия.
Это...
алгоритм

Эти знаки только в паре,
Круглые, квадратные.
Мы все время их встречаем,
Пишем многократно.
Заключаем, как в коробки,
Числа в...
скобки

Три плюс три и пять плюс пять,
Нужно это сосчитать.
Есть знак « плюс » и знак « равно » ,
Может, « минус » — все равно.
Складываем, вычитаем,
Так ... мы решаем.
примеры

Арифметическое действие,
Обратное сложению,
Знак « минус » в нем задействован,
Скажу вам без сомнения.
А в результате разность —
Не зря мои старания!
Пример решил я правильно,
И это...
вычитание

Числа плюсом прибавляем
И ответ потом считаем.
Если « плюс » , то, без сомнения,
Это действие —...
сложение


Задача

Минус

Ответ

Пример

Число

Минус

Незнайка загадал Знайке загадку:
“ Я задумал число,
+ к нему 19, – 27, + 52, – 40 после этого у меня получилось 16.
– Какое число я задумал?"
Знайка составил схему:
решение
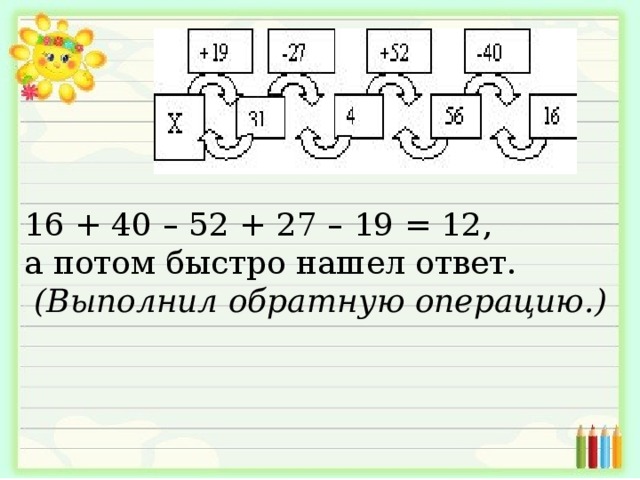
16 + 40 – 52 + 27 – 19 = 12,
а потом быстро нашел ответ.
(Выполнил обратную операцию.)

Перед вами 7 строк последовательно расположенных цифр:
1 2 3 = 1 1 2 3 4 = 1 1 2 3 4 5 = 1 1 2 3 4 5 6 = 1 1 2 3 4 5 6 7 = 1 1 2 3 4 5 6 7 8 = 1 1 2 3 4 5 6 7 8 9 = 1
Не меняя порядка расположения цифр, поставьте между ними знаки арифметических действий и скобки с таким расчётом, чтобы в результате этих действий в каждом ряду получилось бы по 1. При необходимости две рядом стоящие цифры можно считать двузначным числом.
решение
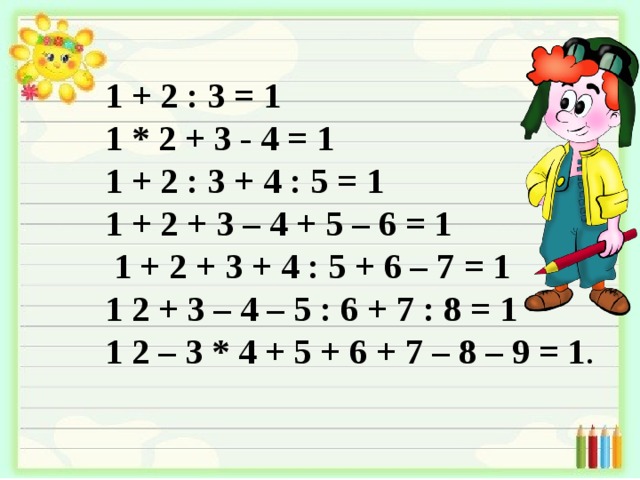
1 + 2 : 3 = 1
1 * 2 + 3 - 4 = 1
1 + 2 : 3 + 4 : 5 = 1
1 + 2 + 3 – 4 + 5 – 6 = 1
1 + 2 + 3 + 4 : 5 + 6 – 7 = 1
1 2 + 3 – 4 – 5 : 6 + 7 : 8 = 1
1 2 – 3 * 4 + 5 + 6 + 7 – 8 – 9 = 1 .

В следующем равенстве необходимо передвинуть одну цифру так, чтобы оно стало верным:
101 – 102 = 1

Миша танки собирает И с друзьями в них играет. У него уже их восемь. И он друга Федю просит Пять из них который год Поменять на вездеход. Только Федя не согласен! Но меняться хочет Вася. Поменялся Миша с ним – Дал три танка за один. Сколько их теперь у Миши, Ночью сосчитают мыши.
8-3+1=6

Математику могут изучать только очень внимательные люди, способные замечать закономерности. Попробуйте указать, какое число будет следующим в каждом ряду и объяснить почему
-2; -5; -8; -11; -14 …
-2; -3; -5; -8; -13 …

+(-3)
+(-3)
; -17
;-20…
-2; -5; -8; -11; -14 …
+(-3)
+(-1)
+(-5)
;-19
;-25
-2; -3; -5; -8; -14 …
+(-2)
+(-4)

Вы спросите : Кто я такая? Координатная прямая! Я прямая без сомненья И имею направленье, Для облегчения подсчёта 0 – начало для отсчёта У меня есть много дочек – Красивых ярких точек. Координатной точки является что? Положение что показывает число: Справа от начала 0 Положительное звено: Плюс 1, плюс 3, плюс 5, Плюсов их не сосчитать;
А слева отрицательные, Не доброжелательные, Числа минус впереди. Лучше с ними не шути! Посередине никакой Расположился важный ноль Без минусов, не идеален, И как все нули нейтрален.

Всем привет! Кто я? Число! 2 иль 5 мне всё равно, Имею брата схожего, но Мне противоположного. Мы так похожи забияки, Но разные имеем знаки. Только каждое число Имеет противоположное одно! А 0, представь себе, Противоположен сам себе.

Раскроем секрет, но это не тайна, Ученые решили ,так не случайно: Натуральные и противоположные числа, Ноль образуют целые числа!

Число что, вот я герой! Рассчитаю расстоянье до точки любой, От начала отсчёта до точки А, Я самый великий! Я модуль числа! Ко всем я уважительный, Всегда я положительный, Для положительных, нуля Силы свои не трачу я , А для отрицательных, Я минус забирательный.

Вот числа -7 и 3. Кто из них больше, посмотри! Есть правило на то одно: Любое отрицательное меньше, чем положительное число. А если с минусом 3 взять, Что больше, трудно мне сказать, Но коль на улице зима, И дует ветер зверь, Понятно даже малышу, При – трех теплей! Из двух чисел отрицательных меньше то, Которое имеет модулем большее число. 0 больше отрицательных чисел всегда, Но меньше положительных, вот беда. На горизонтальной прямой координат Точки с большей координатой правее меньшей лежат.

Задание 1
Задание 2

Попробуй сам составить задачу с отрицательными числами,
ведь они нас окружают повсюду.
Например:
Нина носит очки -1,5 диоптрии. Доктор прописал ей делать гимнастику для глаз, но Нина его не послушалась. В результате ее зрение испортилось на 1 диоптрию. Какие очки следует носить Нине сейчас?
Решение: -1,5-1=-2,5

Выбери два города России и отслеживай ежедневно дневную температуру в течение недели.
По полученным данным найди разницу температурных режимов.
Высчитай среднею температуру за неделю в каждом выбранном городе и посчитай разницу в средних температурах этих городов.
В Красноярске ….. - 6
В Москве ……… + 4
Например:

1. Круги Эйлера
2. Определения множеств чисел
3. Натуральные числа
4. Целые числа
5. Рациональные числа
6. История отрицательных чисел

Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера .
Леонард Эйлер жил в России в
середине XYΙΙΙ века и внес большой вклад
в развитие математики.

Для счета предметов используются числа , которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis , «естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z - первой буквой
немецкого слова Zahl - «число».
Множество чисел, которое можно представить в виде ,
называется множеством рациональных чисел и обозна-
чается- Q первой буквой французского слова Quotient
- «отношение».

Натуральные числа возникли в силу необходимости вести счет любых предметов.
Натуральные числа несут ещё
другую функцию –
характеристика порядка предметов,
расположенных в ряд .
1 2 3 4 5 6 7 8 9 10 …
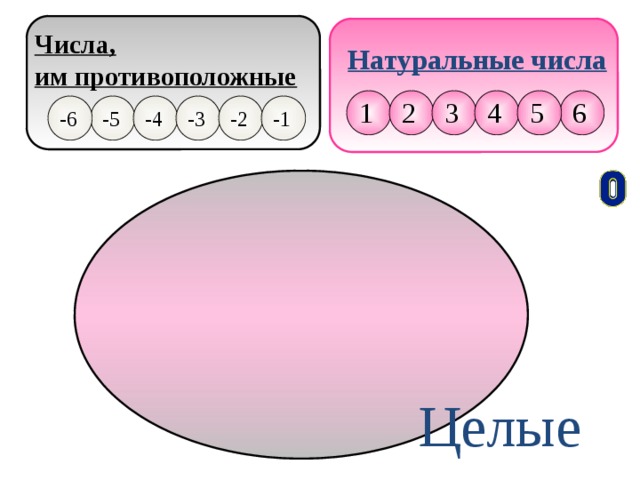
Числа,
им противоположные
Натуральные числа
5
4
6
3
2
1
-4
-3
-5
-2
-1
-6
Целые

Целые числа
Дробные числа
58
10
9
-4
0
1
2/7
0,1
0,(2)
3,2
7,1
Рациональные

Первое упоминание отрицательных чисел мы находим в книге «Математика в девяти главах» китайского ученого Чжан Цань.
Все началось в Китае, примерно во II веке до н.э. Возможно, в Китае их знали и раньше, но первое упоминание относится именно к тому времени. Там стали применять отрицательные числа и считали их «долгами», при этом положительные называли «имуществом». Той записи, которая существует сейчас, тогда не было, и отрицательные числа записывали черным цветом, а положительные красным

Известны индийские ученые Брахмагупта Бхаскара (VII-VIII века), которые в своих учениях оставили подробные объяснения работе с отрицательными числами.
Правда, в Китае к ним, все-таки относились осторожно, старались их применение свести к минимуму, а в Индии, напротив, они использовались очень широко. Там с ними производились вычисления и отрицательные числа не казались чем-то непонятным.

Индийский математик Брахмагупта
(VII век) уже рассматривал их
наравне с положительными.
Вот как он излагал правила сложения
и вычитания: «Сумма двух имуществ есть имущество». «Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности ».

Древнегреческий математик Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа.

в Европе отрицательные числа не признавали очень долго. Их считали «мнимыми» и «абсурдными». Никаких действий с ними не совершали, а просто отбрасывали, если ответ получался отрицательным. Считали, что, если из 0 вычесть любое число, то ответом будет 0, так как ничто не может быть меньше нуля — пустоты.
В Европе отрицательные числа появились благодаря Леонардо Пизанскому (Фибоначчи), который тоже ввёл их для решения финансовых задач с долгами.

В Европе отрицательные числа появились благодаря Леонардо Пизанскому (Фибоначчи), который тоже ввёл их для решения финансовых задач с долгами. В 1202 году он впервые использовал отрицательные числа для подсчёта своих убытков.

Позже, в 1544 году Михаил Штифель в книге «Полная арифметика» впервые ввел понятие отрицательных чисел и подробно описал действия с ними. «Нуль находится между абсурдными и истинными числами».

А в XVII веке математик Рене Декарт предложил откладывать отрицательные числа на цифровой оси слева от нуля.

В 1831 году Гаусс называл отрицательные числа абсолютно равнозначными с положительными. А то, что не все действия с ними можно совершать не считал чем -то страшным, с дробями, например, тоже не все действия можно делать.

в XIX веке Уильман Гамильтон и Герман Грассман создали полную законченную теорию отрицательных чисел. С этого времени отрицательные числа обрели свои права и сейчас уже никто не сомневается в их реальности.

1. Координатная прямая
2. модуль
3. Повтори правила
4. Опорная схема
5. Правила в стихах
6. Сложение двух отрицательных чисел
7. Сложение чисел с разными знаками
8. Вычитание чисел
9. Умножение чисел
10. Деление чисел
11. Правило знаков
12. Действия с 0 и 1
13. Умножение в длинных примерах

Координатная прямая – это прямая с указанными на ней началом отсчета, направлением отсчета и единичным отрезком
Х
Положительные числа
Отрицательные числа
0
Числа, расположенные справа от нуля,
являются положительными ;
числа , расположенные слева от нуля
являются отрицательными.

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А( а )
А(а)
0
а единиц
Обозначают: |а|

- Модуль положительного числа равен самому числу.
- Модуль отрицательного числа равен противоположному числу.
- Модуль 0 равен 0.
- Модуль числа не может быть отрицательным.
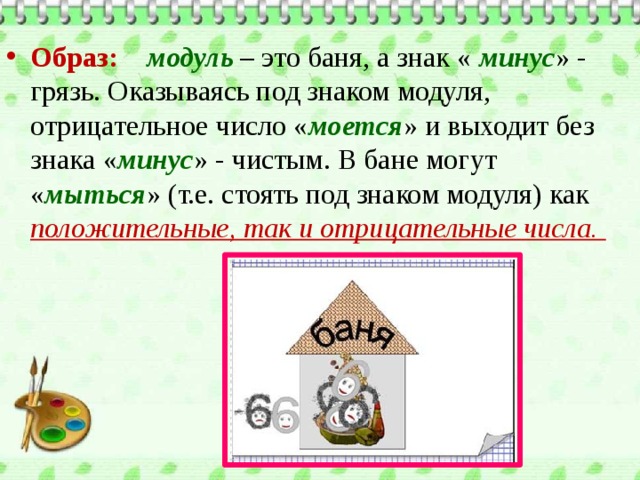
- Образ: модуль – это баня, а знак « минус » - грязь. Оказываясь под знаком модуля, отрицательное число « моется » и выходит без знака « минус » - чистым. В бане могут « мыться » (т.е. стоять под знаком модуля) как положительные, так и отрицательные числа.

противоположные числа имеют равные модули.
│ 5│ = 5 │- 5│ = 5
- 5
││
0
5
5 единиц
5 единиц

Повтори правила.
- (-)+(-)=(-)модули складываем
- (-)+(+)=(?)модули вычитаем, ставим знак большего модуля
- (-)*(-)=(+) (-)*(+)=(-)
- (-): (-)=(+) (-):(+)=(-)
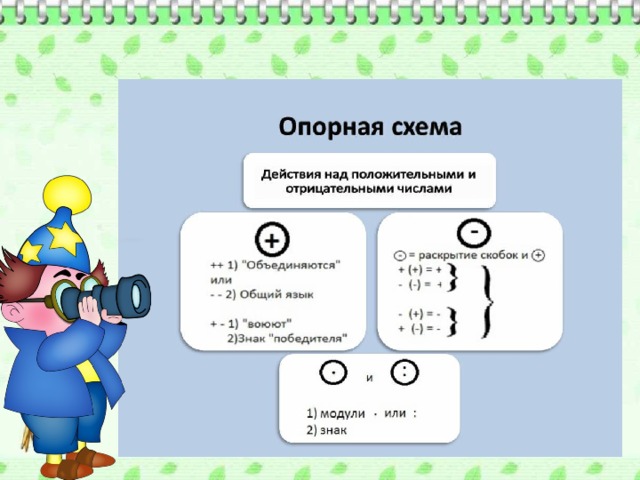

Сложение отрицательных чисел и чисел с разными знаками Если уж захочется вам сложить Числа отрицательные, нечего тужить: Надо сумму модулей быстренько узнать, К ней потом знак «минус» взять да приписать. Если числа с разными знаками дадут, Чтоб найти их сумму, все мы тут как тут. Больший модуль быстро очень выбираем. Из него мы меньший вычитаем. Самое же главное – знак не позабыть! - Вы какой поставите? – мы хотим спросить - Вам секрет откроем, проще дела нет, Знак, где модуль больше, запиши в ответ.

Правила сложения положительных и отрицательных чисел
Минус с минусом сложить, Можно минус получить. Если сложишь минус, плюс, То получится конфуз?! Знак числа ты выбирай Что сильнее, не зевай! Модули их отними, Да все числа помири!

*Сложение двух отрицательных чисел
*Сложение отрицательных чисел (с примером)

Чтобы сложить два отрицательных числа, надо:
- сложить их модули;
- поставить перед полученным числом знак «–»
(Сумма двух отрицательных чисел – отрицательное число)
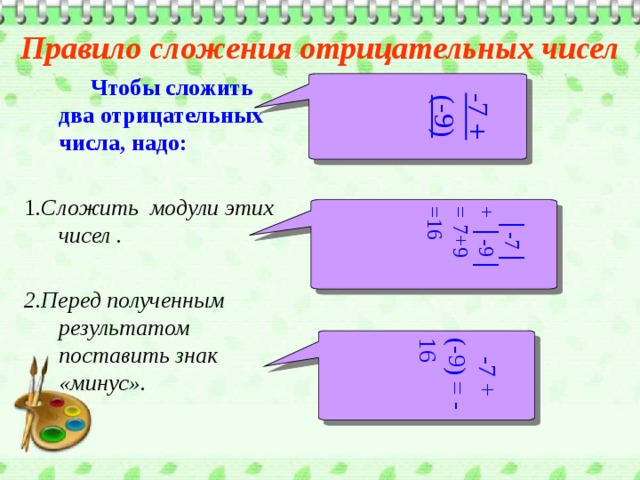
-7 + (-9)
│ -7│ + │-9│ = 7+9 =16
-7 + (-9) = - 16
Правило сложения отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
1 .Cложить модули этих чисел .
2.Перед полученным результатом поставить знак «минус».

*Сложение чисел с разными знаками
*Сложение чисел с разными знаками (с примером)

Чтобы сложить два числа с разными знаками, надо:
- Из большего модуля вычесть меньший;
- поставить перед полученным числом знак того слагаемого модуль которого больше.
(Сумма двух чисел с разными знаками – может быть как отрицательным так и положительным число)
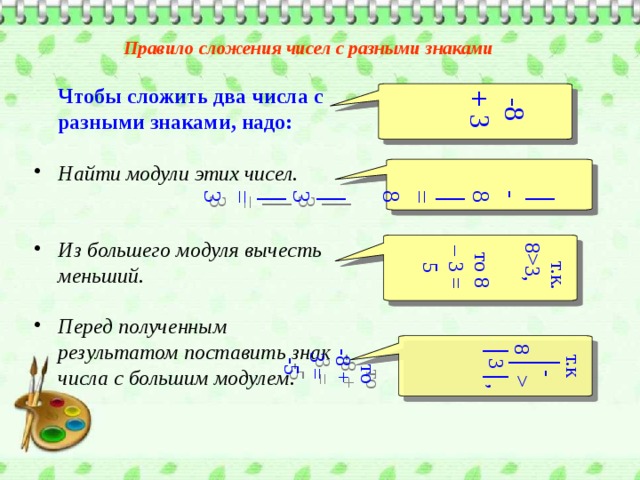 │3│, то -8 + 3 = -5 т.к. 83, то 8 – 3 = 5 Правило сложения чисел с разными знаками Чтобы сложить два числа с разными знаками, надо: Найти модули этих чисел. Из большего модуля вычесть меньший. Перед полученным результатом поставить знак числа с большим модулем. " width="640"
│3│, то -8 + 3 = -5 т.к. 83, то 8 – 3 = 5 Правило сложения чисел с разными знаками Чтобы сложить два числа с разными знаками, надо: Найти модули этих чисел. Из большего модуля вычесть меньший. Перед полученным результатом поставить знак числа с большим модулем. " width="640"
-8 + 3
│ -8│=8 │3│=3
т.к │-8│ │3│, то -8 + 3 = -5
т.к. 83,
то 8 – 3 = 5
Правило сложения чисел с разными знаками
Чтобы сложить два числа с разными знаками, надо:
- Из большего модуля вычесть меньший.
- Перед полученным результатом поставить знак числа с большим модулем.

*Вычитание чисел
*Вычитание чисел (с примером)

Чтобы из одного числа вычесть другое, надо: к уменьшаемому прибавить число, противоположное вычитаемому.
a – b = a + (– b)
Вывод:
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
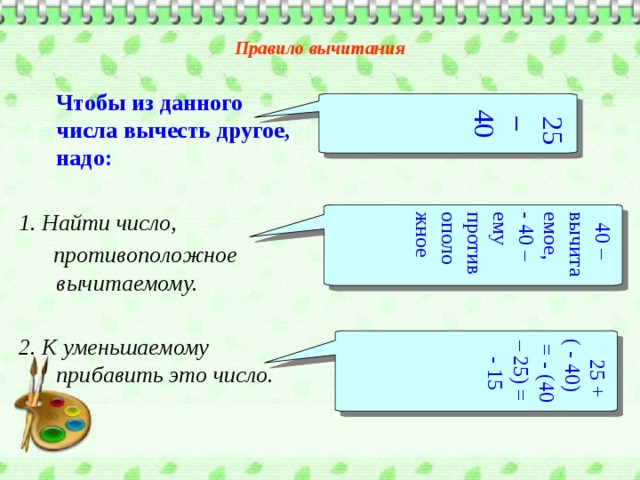
25 – 40
40 – вычитаемое,
- 40 – ему противоположное
25 + ( - 40) = - (40 – 25) = - 15
Правило вычитания
Чтобы из данного числа вычесть другое, надо:
1. Найти число,
противоположное вычитаемому.
2. К уменьшаемому прибавить это число.

*Умножение двух отрицательных чисел
*Умножение чисел с разными знаками
*другое толкование правила

Чтобы умножить два числа с одинаковыми знаками надо:
1) перемножить модули чисел;
2) перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Чтобы умножить два числа с разными знаками, надо:
1) перемножить модули чисел;
2) перед полученным произведением поставить знак «-».

Правила умножения можно истолковать и таким образом: «Друг моего друга - мой друг»: + ∙ + = + «Враг моего врага - мой друг»: ─ ∙ ─ = + «Друг моего врага - мой враг»: + ∙ ─ = ─ «Враг моего друга – мой враг»: ─ ∙ + = ─

*Деление двух отрицательных чисел
*Деление чисел с разными знаками

Чтобы разделить два числа с одинаковыми знаками, надо:
1) модуль делимого разделить на модуль делителя;
2) перед результатом поставить знак «+».

Чтобы разделить два числа с разными знаками, надо:
1) модуль делимого разделить на модуль делителя;
2) перед результатом поставить знак «-».

Правило знаков для чисел
+ (+) = +
+ (-) = -
- (-) = +
- (+) = -

Действия с нулем и единицей:
0 • a = 0
a • 0 = 0
a • 1 = a
0 - a = - a a - 0 = a a - a = 0
0 : а=0
На нуль делить нельзя !
а : 1=а

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве - отрицательным.
Пример.
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 • 3 • 4 • 2 • 12 • 1 = 1728 Конечный результат умножения исходных чисел будет:
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = - 1728

1. Тренажер (отработка отдельно каждого действия)
2. Тренажер с выбором уровня
3. Тренажер (тест на scratch)

СЛОЖЕНИЕ
ВЫЧИТАНИЕ
УМНОЖЕНИЕ
ДЕЛЕНИЕ

9+(-5)=
4
14
-4

-8+(-4)=
4
12
-12

-19+2=
-21
-17
17

6+(-1)=
-7
5
7

-25+30=
-5
5
55

8
4
-8
2-(-6)=
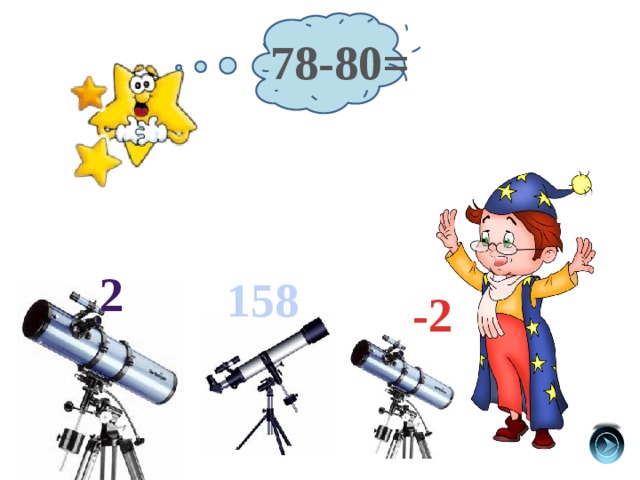
78-80=
2
158
-2

-9-5=
-14
14
4

64-70=
134
6
-6

6
-6
10
8-(-2)=
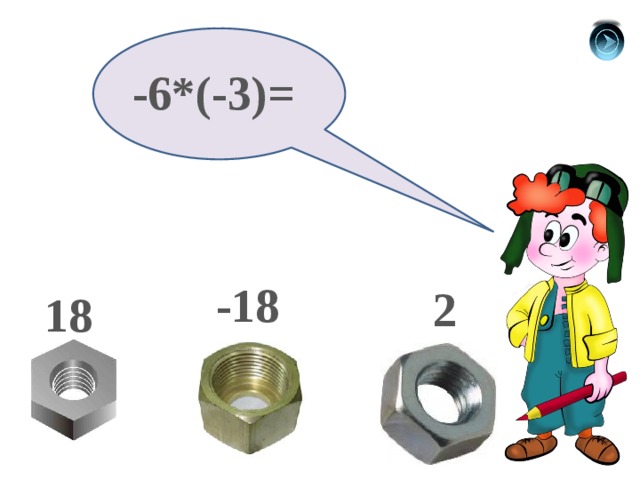
-6*(-3)=
-18
2
18
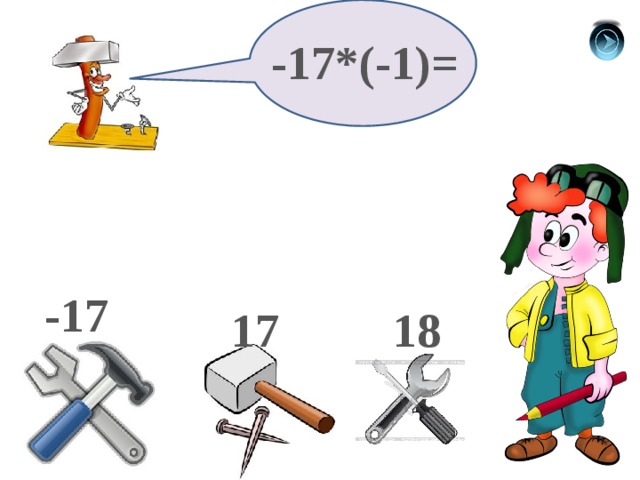
-17*(-1)=
-17
17
18
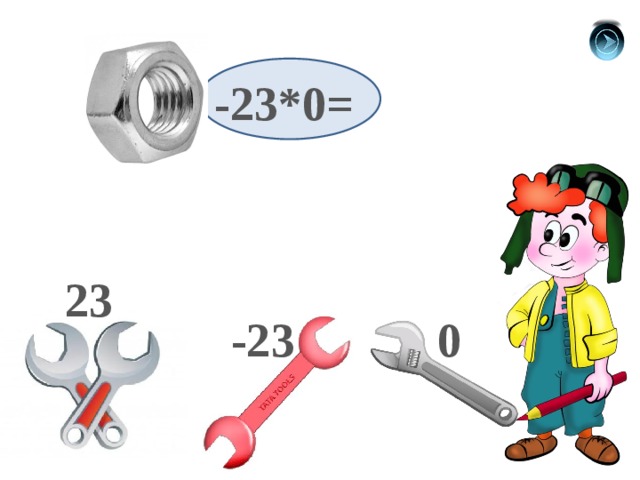
-23*0=
23
-23
0

-8*6=
-48
48
14

-5*5=
25
-25
0
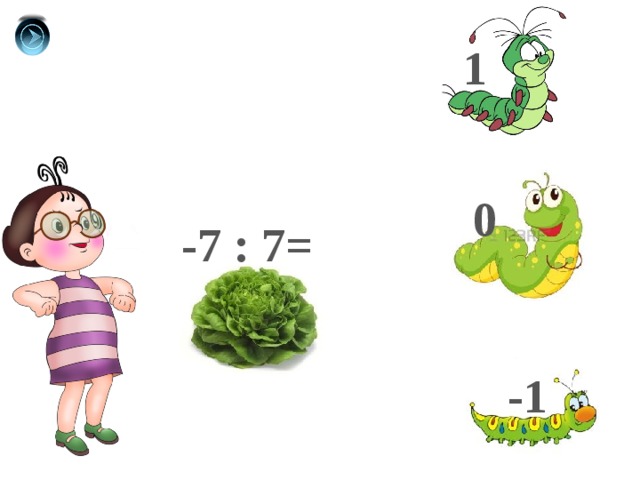
1
0
-7 : 7=
-1

15
18: (-3)=
6
-6

18
-1
18: (-1)=
-18

2
-14: (-7)=
-2
-7

нельзя
-98:0=
0
-98


правила
пуск
подсказка
выход

Правила :

Подсказки:
- (-)+(-)=(-)модули складываем
- (-)+(+)=(?)модули вычитаем, ставим знак большего модуля
- (-)*(-)=(+)
- (-)*(+)=(-)
- (-) : (-)=(+)
- (-) : (+)=(-)

1 уровень
2 уровень

57
-27+(-30)=
-3
-57

27
5+(-32)=
-37
-27
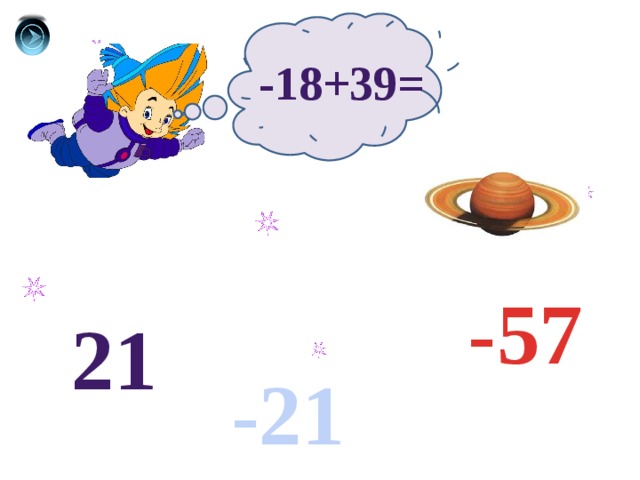
-18+39=
-57
21
-21

1-88=
89
87
-87

39
-39
-36
-13*3=

67
29
-67
-19-48=

11
10
-10
-110: (-11)=

-38
-27-11=
38
-16

13-47=
24
60
-24

-57
Нет ответа
0
0 : (-57)=

конец
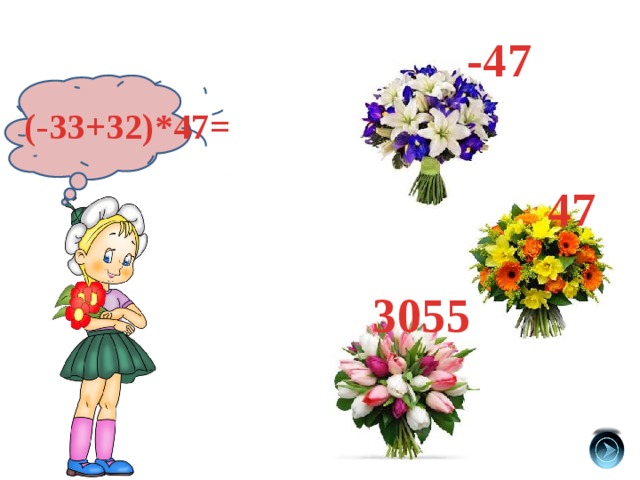
-47
(-33+32)*47=
47
3055

250
300
-50*(-2)+(-3)=
-300

1
-1
-5
(-1)*(-1)*(-1)*(-1)*(-1)=
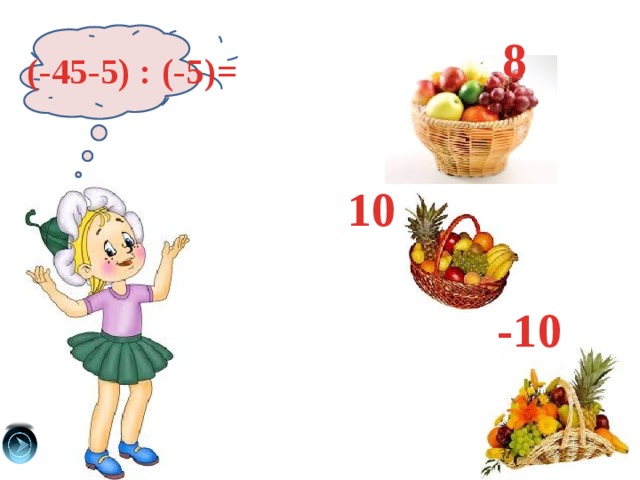
8
(-45-5) : (-5)=
10
-10
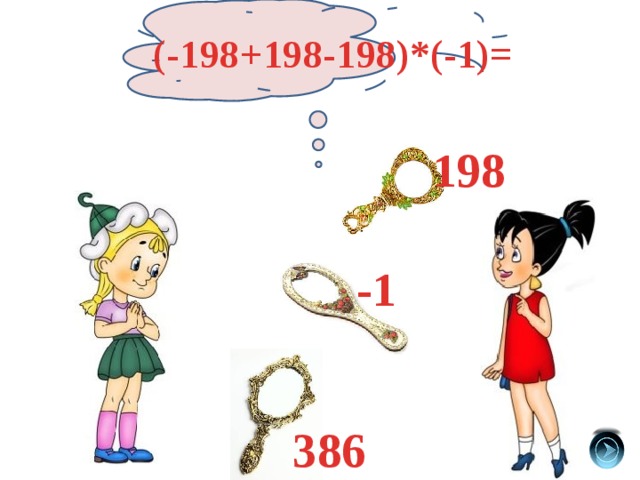
(-198+198-198)*(-1)=
198
-1
386
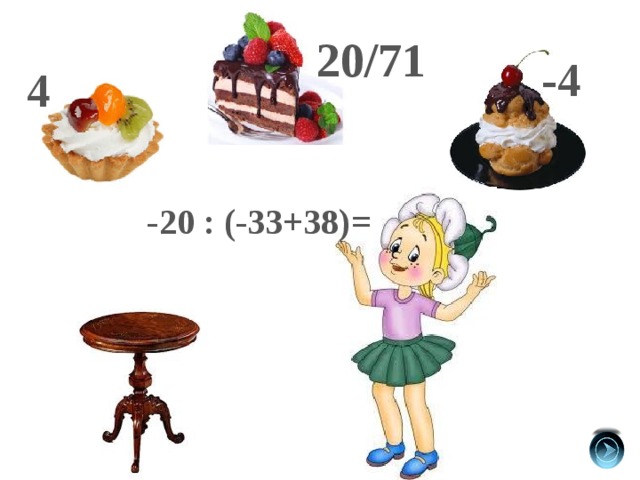
20/71
-4
4
-20 : (-33+38)=

-2
2
(18-40) : (-11)=
5
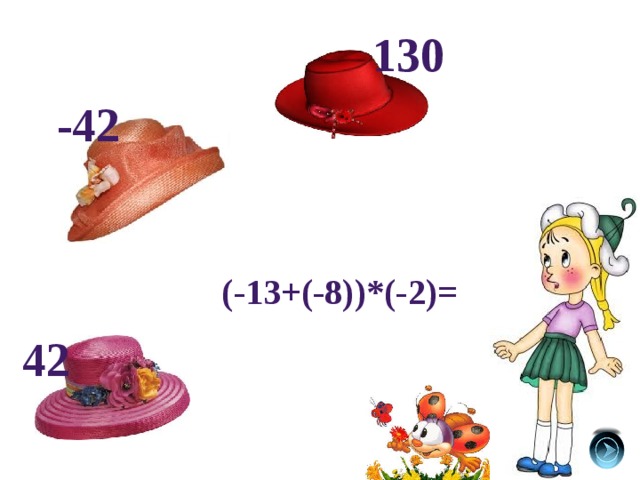
130
-42
(-13+(-8))*(-2)=
42
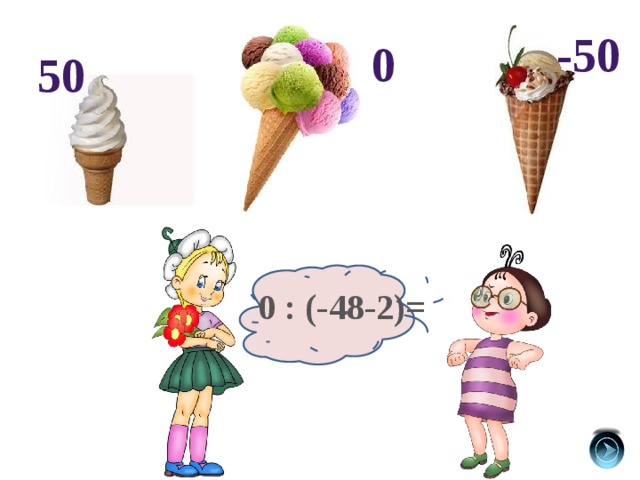
-50
0
50
0 : (-48-2)=

53
-110
55*(-17+15)=
111

конец

https://scratch.mit.edu/projects/64171018/#player


Устный счет

Практика

Связь с другими предметами

Опрос теории

Игра-ходилка
Игра 1
Игра 2
Игра 3

Игры, ребусы…




игра1

Игра 2

Игра 3

Мир чисел
Круги Эйлера

*Сложение отрицательных чисел
*Сложение отрицательного и положительного чисел


Правила, опорные схемы














































 -7 -47 … + (-3) -45 + … 13 … + (-60) 14 + … -21 Сравните -20 -70 33 + … … + 49 -6 0 … + (-70) -14 + … -19 + … 13 … + (-13) 13 2 вариант 1 вариант 15 + (-2) " width="640"
-7 -47 … + (-3) -45 + … 13 … + (-60) 14 + … -21 Сравните -20 -70 33 + … … + 49 -6 0 … + (-70) -14 + … -19 + … 13 … + (-13) 13 2 вариант 1 вариант 15 + (-2) " width="640"

































 у, х 0, у 0. " width="640"
у, х 0, у 0. " width="640"


















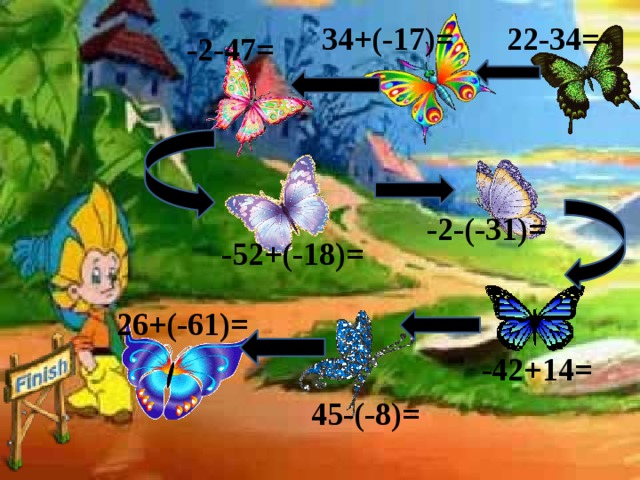


























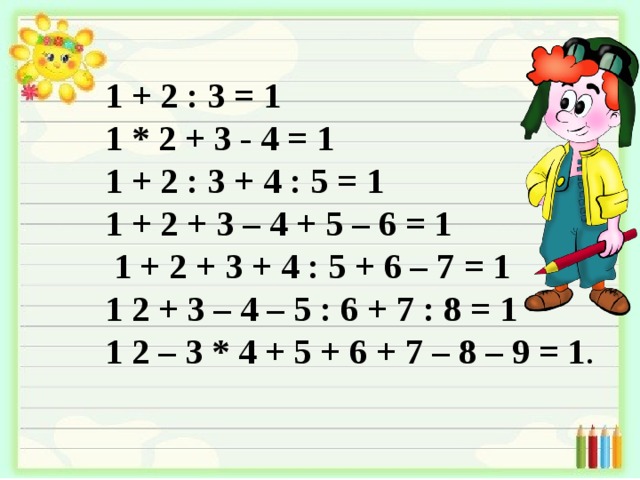











































 │3│, то -8 + 3 = -5 т.к. 83, то 8 – 3 = 5 Правило сложения чисел с разными знаками Чтобы сложить два числа с разными знаками, надо: Найти модули этих чисел. Из большего модуля вычесть меньший. Перед полученным результатом поставить знак числа с большим модулем. " width="640"
│3│, то -8 + 3 = -5 т.к. 83, то 8 – 3 = 5 Правило сложения чисел с разными знаками Чтобы сложить два числа с разными знаками, надо: Найти модули этих чисел. Из большего модуля вычесть меньший. Перед полученным результатом поставить знак числа с большим модулем. " width="640"